有源降噪中电声器件频率响应的仿真研究
2021-11-17何彦兴曾庆宁
何彦兴,曾庆宁
(桂林电子科技大学信息与通信学院,广西 桂林 541004)
1 引言
有源噪声控制(active noise control,ANC)系统是基于破坏性干扰原理的电声装置[1],通过产生反向噪声来衰减目标场区的噪声信号达到降噪的目的。在降低传统无源噪声控制技术无法衰减的低频噪声方面,该方法表现出了良好的性能。ANC系统最广泛使用的自适应控制算法之一是FxLMS算法[2-3]。该算法与LMS算法最大的区别在于引入了次级通路,由于次级通路的存在,误差梯度的瞬时值不再是真实梯度的无偏估计[4],在使用参考信号(在环境中拾取的声压)之前需将其通过辅助路径的估计模型进行滤波。次级通路建模[5-7]一般分为自适应离线建模和自适应在线建模两大类。如果在ANC系统运行时,次级通路的特性基本保持稳定,则可以使用自适应滤波器或其它 横向FIR滤波器提前确定次级通路的传递函数。当系统特性经常发生改变,为了确保有源降噪系统的稳定性与降噪量,则需要选择在线辨识的方法[8-9]。
实际上噪声信号经过声-电-声的模数转换后,其波形往往会发生变化甚至产生严重失真,导致自适应滤波器无法有效跟踪辅助白噪声的变化从而得到的次级通道模型与实际情况相差甚远。目前,有源噪声控制系统所使用的电声系统绝大部分为电动扬声器搭配传声器的组合,在进行主动噪声控制系统仿真时,一般默认采放音设备为理想状态,即其灵敏度为1,而忽略其频率响应对处在不同频率信号的幅值所造成的衰减。然而,实际的采放音设备与所假设的理想状态不同,电声器件的频率响应会使不同频率下输出信号幅值受到不同的衰减,这将导致ANC系统的实际消噪效果与理想仿真结果之间存在差距。经查阅相关文献,对ANC系统次级通路建模中电声系统模型方面研究较少。湖南大学的聂永红[10]等通过电力声类比线路方法建立了次级声源的非线性时域模型,并将其引入ANC系统进行仿真,研究了该模型对控制系统收敛范围的影响。本文分析了有源降噪中电声系统部分的频响特性,采用有限脉冲响应滤波器来逼近次级声源与传声器的频率响应曲线,以FxLMS算法为例,对控制系统在不同情况下的消噪效果进行了仿真研究。
2 有源噪声控制系统
2.1 ANC系统结构
典型的单通道自适应有源噪声控制系统[11]如图1(a)所示(以自由声场为例)。有源噪声控制系统包括两部分:控制器和传感-作动部分,传感-作动部分的器件包括参考传声器、误差传声器和次级声源。
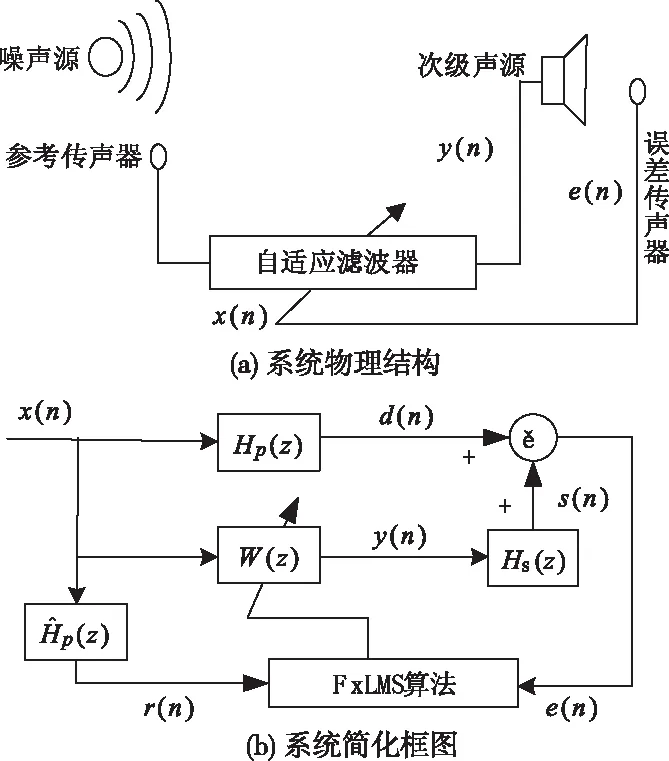
图1 ANC系统物理结构和简化框图
系统工作的流程如下:噪声源处的噪声信号由参考麦克风拾取,将经过声-电转换后的采集信号x(n)送至自适应滤波器进行信号处理,控制器根据设定的控制算法产生反向的次级干扰信号y(n)。驱动次级声源输出y(n)形成次级声场,与噪声场在目标场区进行叠加相消。叠加声信号由误差传声器进行拾取,记为误差信号e(n)。作为一种控制信号,误差信号同时也是ANC系统降噪效果判别的依据,自适应控制器根据e(n)的大小对滤波器的权系数进行调整,确保控制算法不断收敛,直到系统达到稳定状态。
图1(b)为系统的简化框图,自适应滤波器采用有限脉冲响应结构,将其权系数记为W(z),由滤波-xLMS算法实时更新;Hp(z)和Hs(z)分别为噪声源及次级声源到目标场区的声通道传递函数;s(z)为Hs(z)的估计。
2.2 FxLMS算法原理
设滤波器长度为L,将第n时刻自适应滤波器的权系数和参考输入表示为矢量形式,经典FxLMS算法推导过程[12-13]如下
W(n)=[w1(n),w2(n),…,wi(n)]T
(1)
X(n)=[x1(n),x2(n-1),…,xi(n-i+1)]T
(2)
L阶滤波器的输出y(n)为
=wT(n)x(n)=xT(n)w(n)
(3)
由上可知,经FIR滤波器得到的控制信号y(n)并不等于目标场区的反向叠加信号,需要通过次级通道模型的相互转换。假设初级噪声具有局部平稳特性,可以认为自适应滤波器权系数在L时段内基本不变[5],控制器产生的反向信号s(n)等于LMS滤波器输出与次级通道脉冲响应的卷积为
=rT(n)w(n)
(4)
其中r(n)被称为滤波-X信号,其与参考信号矢量的卷积关系是
r(n)=x(n)*hs(n)
(5)
于是,目标场区由误差传声器接收到的信号e(n)表示为
e(n)=d(n)+s(n)=d(n)+rT(n)w(n)
(6)
为了使误差信号e(n)的值最小,需要求出滤波器的最佳权系数,在此采用最小均方误差准则来进行迭代
W(n+1)=W(n)-2μe(n)r(n)
(7)
2.3 电声器件的频率响应
当电声器件在一个频率下的传输与其它 频率不同,就会存在频率响应。频率响应一般指幅频响应,它是对电压随频率变化差异的输出结果。不同的电声设备有不同的工作频率范围,在该频率范围上的响应也有一定的幅值差别。
扬声器的频率响应[14]是指在自由声场条件下,在恒定电压(通常是1W正弦波电压)作用下,扬声器在参考轴上离参考点1m处所产生的声压随频率变化的特性。参考点一般定在辐射口平面中心位置,参考轴是通过参考点与辐射口平面垂直的一条直线,为扬声器的最大响应轴,也称为主轴。
传声器的频率响应是自由场平面波入射方向不变的条件下,令传感器主轴垂直于波阵面所测得不同频率是的输出信号电压值。一般来说,传声器的幅频特性曲线[15]应具有频率范围宽、曲线平直的特点以减少采样信号的失真来获得更好的音质。
实际工程应用中所采用电声器件的频率响应曲线图如图2和图3所示。横坐标为信号的频率,纵坐标为电声器件输出的信号声压级,频率响应是这两个参数指标的变化关系。可以看出,信号的声压级与频率相关,在40-110Hz范围内曲线走势陡峭,信号受频率的影响较大,与有源降噪所针对的低频噪声频率范围基本重合。
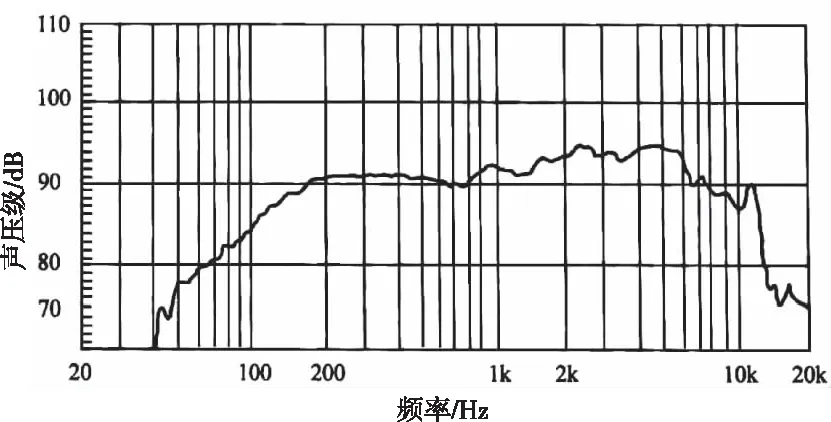
图2 扬声器频率响应曲线[15]
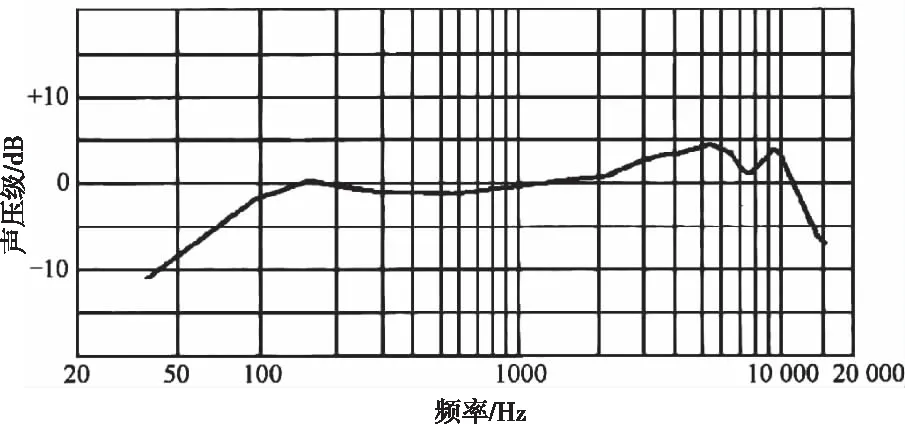
图3 传声器频率响应曲线[16]
3 ANC系统仿真
下面以FxLMS算法为例,采用有限脉冲响应滤波器模拟电声器件的频率响应曲线,研究其在不同情况下与理想情况有源降噪系统的降噪效果差别。
将电声器件的频率响应曲线引入ANC系统进行仿真,假设扬声器与传声器的频响特性基本一致,采用窗函数法建立FIR高通滤波器来逼近该频率响应曲线。滤波器的参数指标为:输出信号在频率40Hz处衰减为-10dB,在频率150Hz处衰减为0dB,窗函数选择hanning窗。FIR滤波器所建立的仿真与理想情况的频率响应曲线如图4,与理想情况平直的频响曲线不同,仿真情况下曲线在20-100Hz的范围内较陡峭,输出信号的衰减在50Hz处为-8.1dB,100Hz处为-1.4dB;在100Hz后曲线走势较平坦,对输出信号的幅值衰减较低。
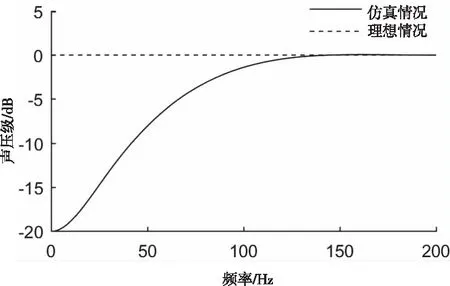
图4 仿真与理想情况下的频率响应曲线
在40-150Hz频率范围内,将电声器件的频响曲线分为陡峭和平直进行讨论,有以下几种情况:
理想情况:传声器和扬声器的频响曲线均是平直的;
情况1:传声器的频响曲线是陡峭的,扬声器的频响曲线是平直的;
情况2:传声器的频响曲线是平直的,扬声器的频响曲线是陡峭的;
情况3:传声器和扬声器的频响曲线均是陡峭的。
下面对不同情况下的电声器件进行ANC系统降噪效果对比与分析。使用等幅值的70Hz、100Hz和140Hz频率叠加正弦信号作为噪声源,测试ANC系统的降噪效果。在70Hz、100Hz频点处幅频特性曲线对信号幅值衰减较大,衰减量为-4.4dB、-1.4dB;在140Hz处的信号衰减可忽略不计。ANC系统在不同频率点的仿真降噪曲线如图5。
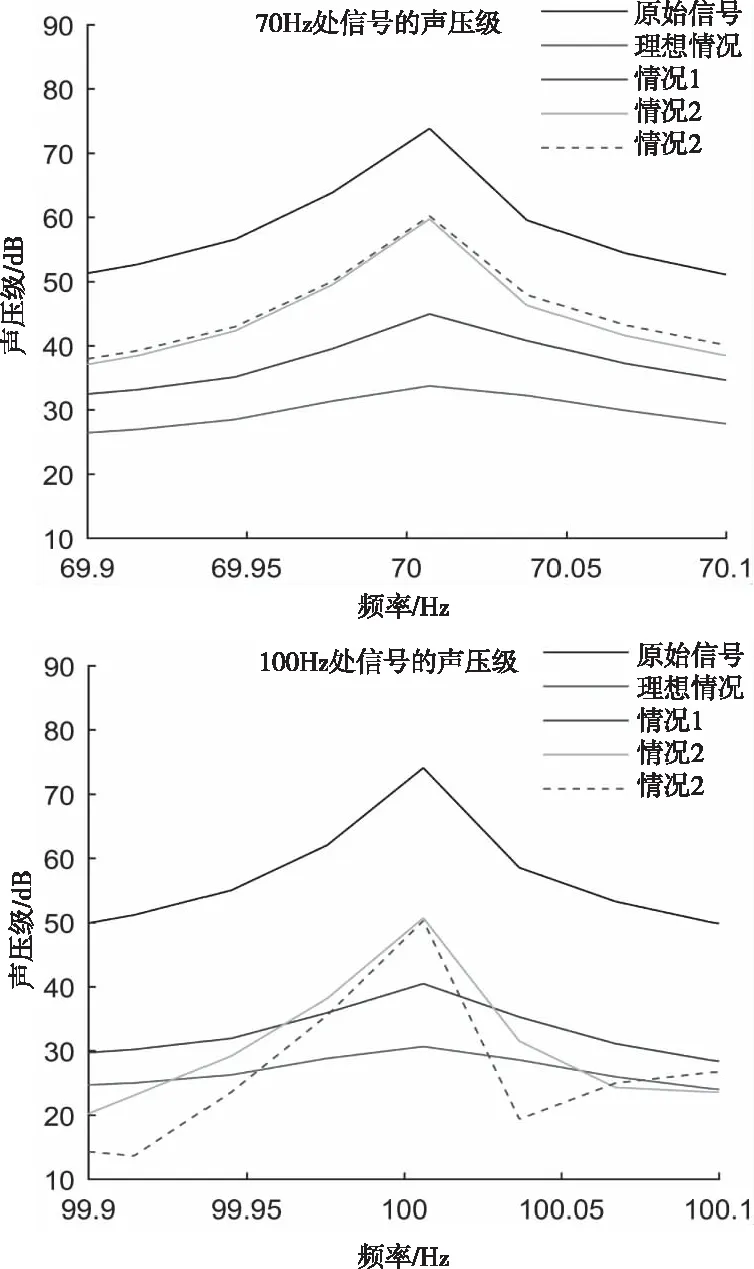
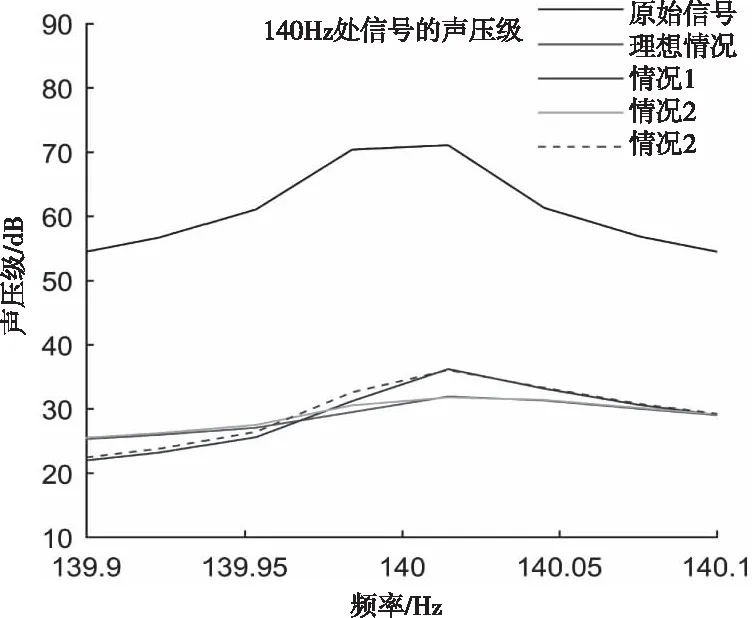
图5 不同情况下的ANC系统仿真曲线
可以看出,当噪声源为混频信号时,不同情况下FxLMS算法的降噪量对比理想情况的降噪量有一定的差距。在频率70Hz和100Hz处,情况1比情况2、3的降噪效果要更好,后两者的降噪曲线走势一致,降噪效果相差不大;在频率为140Hz处,幅频特性曲线对输出信号的衰减不大,因而情况2的降噪量与理想情况一致,情况1与情况3也取得了较好的降噪效果。
在不同情况下3个单频点FxLMS算法仿真前后的声压级如表1所示。在理想情况下ANC系统的降噪效果最好,降噪量可达40-45dB。在频率70、100Hz处,幅频特性曲线对信号幅值的衰减较大,情况1的降噪效果较好,降噪量比情况2、3多降10dB左右,说明情况1中传声器的采集信号经控制系统处理后幅值得到修正,经过理想扬声器输出的反向信号较其它 情况取得更好的降噪效果。在频率140Hz处输出信号基本无衰减,情况2的处理结果比另外两种情况多降4dB以上。说明在情况1、3时,受到衰减的输入信号对自适应滤波器的权矢量系数造成了影响,使ANC系统在140Hz处并未达到最好的消噪效果。
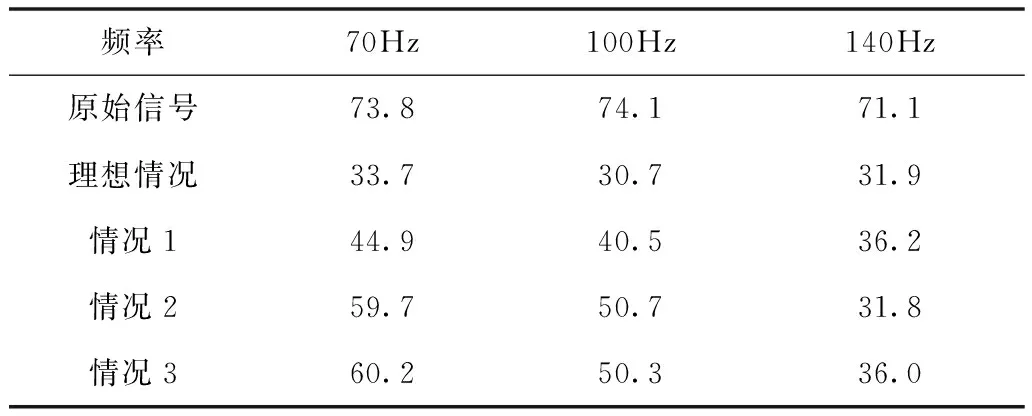
表1 混频信号的降噪量对比
在有源降噪系统的实际应用中,需要消除的噪声一般都不是简单的单频噪声,而是具有一定带宽、频率成分主要为低频的窄带噪声。下面使用某装甲车正常行驶时的实测噪声信号作为噪声源,对系统的降噪效果进行仿真与分析。
图6是电声器件在不同情况下针对实测噪声信号的ANC系统仿真对比图。观察其频谱图可知噪声信号在40-80Hz频率范围内的声压级较高,与电声器件的频响曲线波动的区间重合。仿真图表明电声器件在理想情况下FxLMS算法对于实测噪声信号具有良好的降噪效果;由于幅频特性曲线对输出信号幅值的严重衰减导致另外3种情况在40-150Hz频率范围内的降噪效果较差,与理想情况有一定的差距。对于3种不同情况,在40-90Hz频率范围内情况1的降噪效果最好,情况2跟情况3的降噪曲线走势大致相仿,其在噪声最高频率点60Hz处比情况3多降2dB;当信号频率大于90Hz,情况2在目标场区的降噪效果不断提高,与理想情况的降噪量仅相差2-3dB,情况1的降噪曲线在150Hz频率后与情况3基本一致,且无法取得与情况2一样良好的降噪效果。
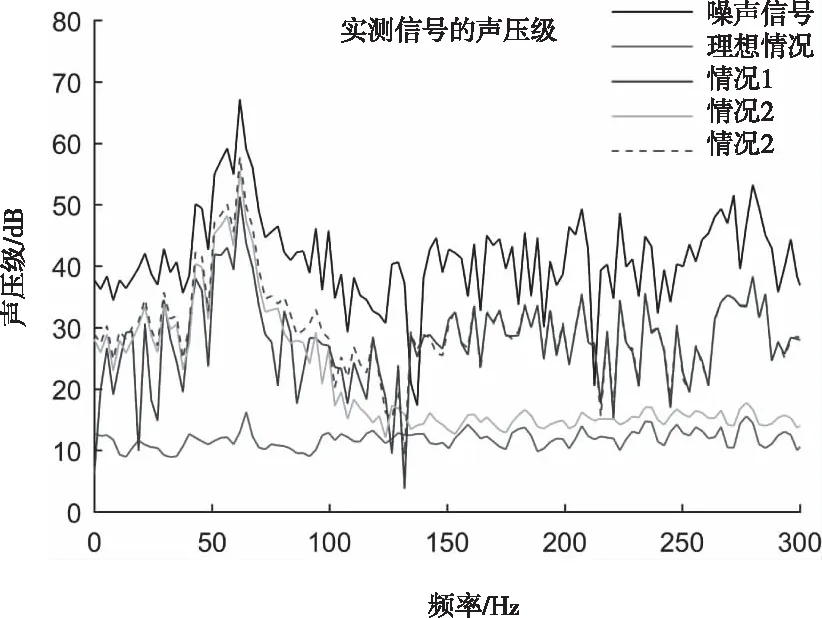
图6 实测信号的降噪曲线
表2是使用FxLMS算法在不同情况下对实测噪声数据进行ANC仿真的平均降噪量。
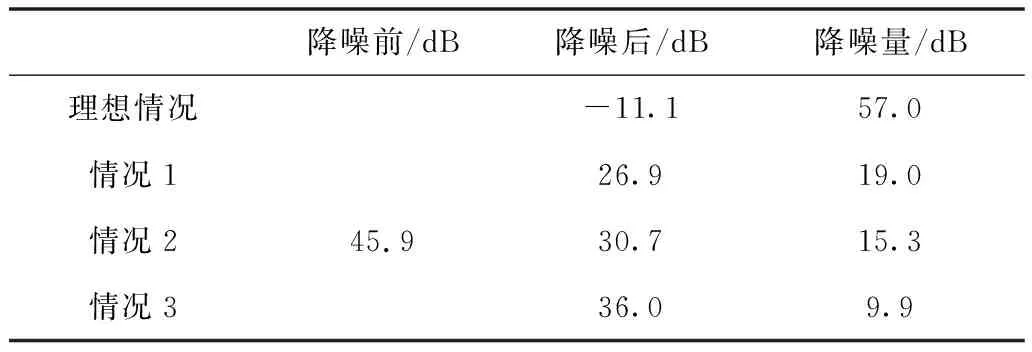
表2 实测信号的降噪量对比
理想情况、情况1、情况2、情况3的降噪量分别为57.0dB、19.0dB、15.3dB、9.9dB。在理想情况下,电声器件平直的频响曲线不会对输入、输出信号的幅值产生非线性变化,因此降噪效果最好;在噪声声压级较高的40-80Hz区域,情况1降噪效果较好,因此情况1的总降噪量比情况2高;情况3中电声器件的频响曲线都不是理想情况,导致ANC系统输出信号与噪声信号的幅值失配现象最严重,因此降噪效果最差。由此可知,在ANC系统的实际应用中,使用离线或在线建模等方法通过自适应滤波器对次级通路进行建模所得到的模型会与真实的次级通道传递函数有一定的偏差,这将导致ANC系统的降噪性能远不能达到采用理想电声器件情况下的主动降噪仿真结果。
4 结束语
本文采用有限脉冲响应滤波器对主动噪声控制系统中电声器件的频响曲线进行了建模并将其引入ANC系统进行仿真,得到以下结论:1)与ANC系统仿真时所采用的理想电声器件不同,实际应用中扬声器与传声器的频响曲线在低频范围往往是变化的,对处于不同频率的信号有不同的衰减;2)对于混合正弦信号或窄带噪声源,频率特性对信号的衰减造成的幅值失配将导致其降噪效果远低于理想情况时的仿真结果;3)在低频范围内,针对电声器件是否具有陡峭频响曲线的不同情况,ANC系统仿真的降噪效果也有差异。
由以上结论可以看出,电声器件陡峭的频率响应曲线确实明显地影响了ANC系统的降噪效果,在系统仿真时应考虑频响特性会对次级通道建模造成的误差。在实际应用中,具有良好频响特性的传声器和扬声器成本较高,将有源降噪系统扩展到多通道时所使用的电声器件数目会成倍提升。因此之后的研究工作主要考虑通过改进算法来抵消电声器件频率响应带来的影响。
