无伞空投影响因素敏感性及载机安全性分析

2021-11-17曾冠霖陈昊翔

计算机仿真 2021年4期

孙旺，南英，曾冠霖，陈昊翔

(1. 南京航空航天大学航天学院，江苏南京 210016；2. 中国航空无线电电子研究所，上海 200241)

1 引言

空投精确性是空投任务的首要指标[1]。目前，对精确空投的研究主要集中在有伞空投。为研究各种不确定因素对无伞空投落点精度的影响，从多种不确定因素中找到关键影响因素，需要使用恰当的数据分析方法，对多种不确定因素进行分析，而敏感性分析法就是目前常用的一种数据分析方法。

根据敏感性分析的作用范围，可以将其分为局部敏感性分析和全局敏感性分析。局部敏感性分析只检验单个属性对模型的影响程度；而全局敏感性分析检验多个属性对模型结果产生的总影响，并分析属性之间的相互作用对模型输出的影响[2]。局部敏感性分析因其在计算方面的简单快捷，固具有很强的可操作性，现在大量实际应用中都是采用这种方法。李健[3]研究了制导工具误差对落点精度的影响分析。刘琦[4]将精确空投着陆误差的影响因素分为制导误差和非制导误差两类，指出影响精确空投系统的着陆精度的因素很多。本文采用层次分析法找出所有影响空投精度的因素，结合局部敏感性分析法和全局敏感性分析法，分析所有单个因素对空投精度的影响，以及多个因素共同作用下对空投精度的影响。

安全性[5]是实际工程项目中必须考虑的因素。载机安全性即表示载机在空投物品释放过程中的飞行稳定性和机身安全性，稳定性是指载机在释放空投物品后由于载机质量之心变化会对载机的姿态稳定产生干扰，但由于空投物品和载机质量相比较小，所以安全性分析中不考虑载机的飞行稳定性问题。机身安全性是指载机在投放空投物品后，空投物品不能和载机发生摩擦或者碰撞，保证载机的安全飞行和空投物品的安全下落。本文将航空器视为圆柱体，只检测空投物品与圆柱体是否发生碰撞。

目前，对无伞空投的研究较少。本文针对无伞空投高度低、无控制等特点，建立了空投物飞行仿真数学模型，详细的分析了不同影响因素对空投精度的影响，以及风场对载机安全性的影响。

2 问题描述

载机从右侧将空投物品弹出，在无随机误差与干扰的条件下，其落点位置是(Xf，Yf)，但是，在真实飞行环境中，决定该落点位置的因素是

Θ=[(H，V，θ，φ)|t=t0,Ix，Iy，Iz，m，θt，Vt…]

(1)

式中，(H，V，θ，φ)|t=t0是空投释放时刻载机的飞行高度、速度、轨迹倾角与偏航角，Ix，Iy，Iz是空投体的转动惯量，m是空投体的质量，Vt与θt是空投时的弹射速度与弹射角度；以上各个因素Θi(i=1，2，3，…，N)中隐含着大量的随机误差与干扰，而使得真实飞行环境中的落点位置是(X(t)，Y(t))|t=tf，由此形成落点距离误差百分比ε，如下所示

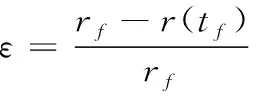
(2)

(3)

(4)

式中，rf是没有随机干扰情况下的落点距离，r(tf)是真实环境中(有随机干扰情况下)的落点距离。

敏感性分析需要从多个因素中逐一找出对项目指标(落点精度)有影响的敏感性因素，并分析其对项目指标的影响程度，进而判断项目承受风险的能力。若某参数的小幅度变化能导致项目指标的较大变化，则称此参数为敏感性因素，反之则称其为非敏感性因素。即需要研究各个影响因素Θi(i=1，2，3，…，N)在不同随机误差下对落点距离误差ε的影响。

同时，载机在空投时需考虑空投物品被投出后是否会碰撞到载机，即

(5)

式中，A和B分别表示载机与空投包的形心坐标，l为机身宽度，D为空投包的宽度，符号║表示范数。

无伞空投影响因素的敏感性分析是一个多属性决策问题，载机安全性分析是一个防碰撞问题。

3 无伞空投飞行仿真建模

空投物品的飞行仿真建模即构建空投物品的飞行运动方程，这些运动方程是表征空投物品的运动规律的数学模型，也是分析、计算和模拟空投物品飞行过程的基础。

空投物品在飞行过程中的运动可分解为质心的空间平动和绕质心的定点转动两部分。为了方便建立描述空投物品运动的数学模型，作出如下假设：

1)地面坐标系为惯性坐标系，视地球表面为平面；

2)不计地球公转和自转的影响；

3)空投物品几何形状对称，质量均匀分布。

实际中并不存在单独的空投物品运动方程，由于空投物品的壳体气动外形，与钝头型航空炸弹结构类似，没有自动控制系统，没有推力系统及减速系统，所以在对空投物品的仿真过程中使用导弹飞行的数学模型[6]，只是去掉其中的控制部分和推力部分，并对其中的气动数学模型进行一些修改，使之更符合空投物品与大气相互作用的实际过程。

模型主要包括：空投包模型、气动力模型和风场模型。

3.1 空投包模型

空投包模型设为长方体，详细参数设置如下：几何特征参数(m)：0.6*0.6*0.9；质量(kg)：80；气动特征长度(m)：0.6；气动特征面积(m2)：0.36。

3.2 气动力计算模型

气动力特性是指空投体下落运动过程中受到的升力、阻力、侧向力等气动力随着气动力参数的变化而表现出来的、符合一定变化规律的特性。气动力参数是影响气动力的直接因素，并进一步作用于空投体的飞行姿态、飞行速度、加速度、角速度等，最终影响落点位置、落点速度。为确定空投体的气动力特性，使用FLUENT软件进行计算，求解定常N-S(Navier-Strokes)方程。对于低速流边界条件使用速度入口，湍流模型使用SST湍流模型，粘性项选用一阶迎风格式，压力项选用二阶顺风格式，动量项使用MUSCL三阶格式，梯度求解选用基于单元的高斯克林函数。

计算状态为速度70m/s，高度0m，大气参数如表1所示，迎角0～100°、侧滑角0～30°，气动特性计算结果如图1-6所示。其余工况可通过插值求得。

图1 升力系数～迎角曲线

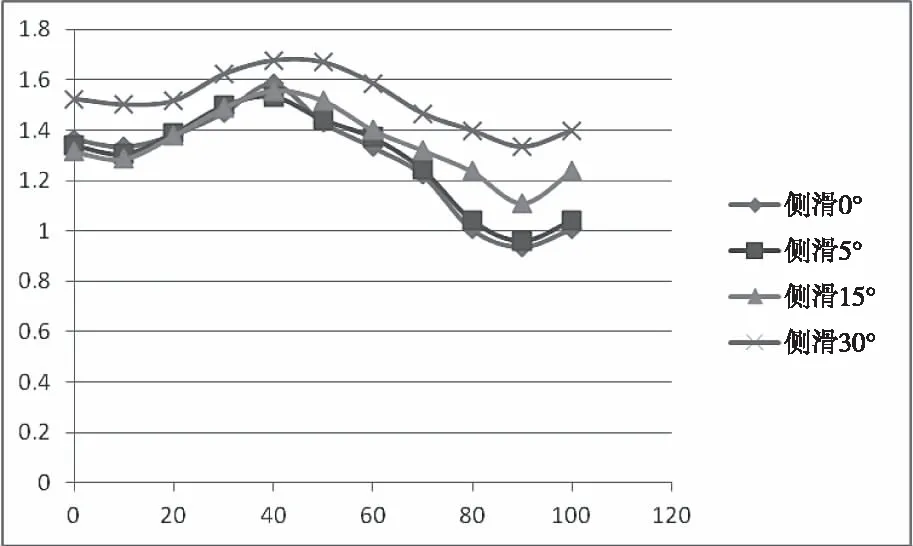
图2 阻力系数～迎角曲线

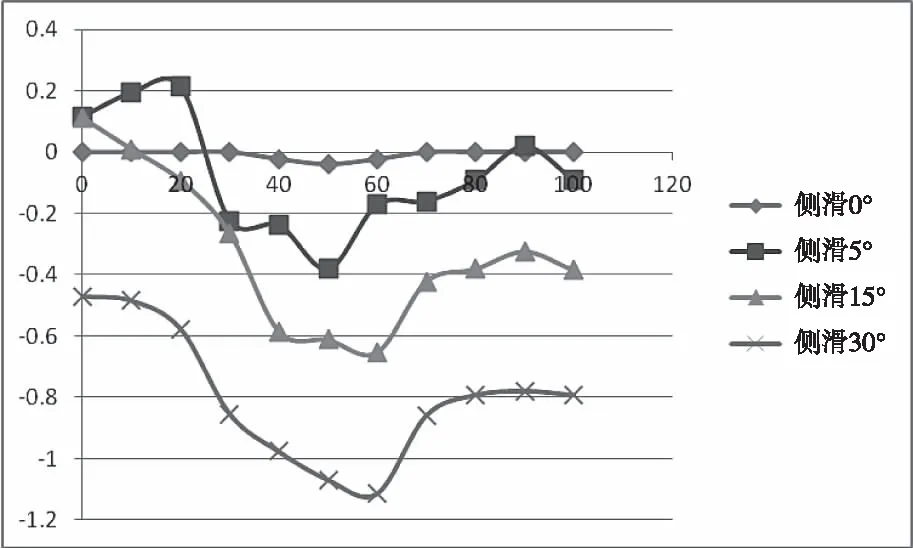
图3 侧向力系数～迎角曲线

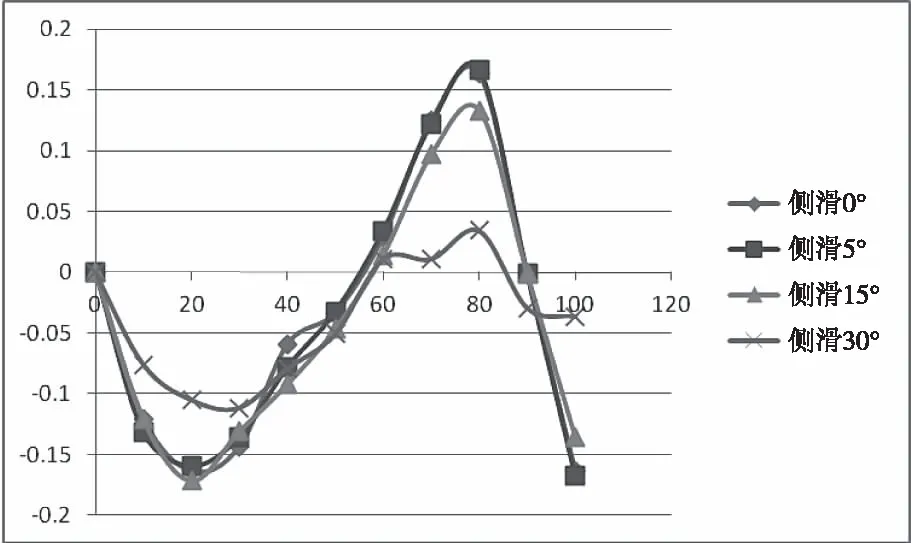
图4 俯仰力矩系数～迎角曲线

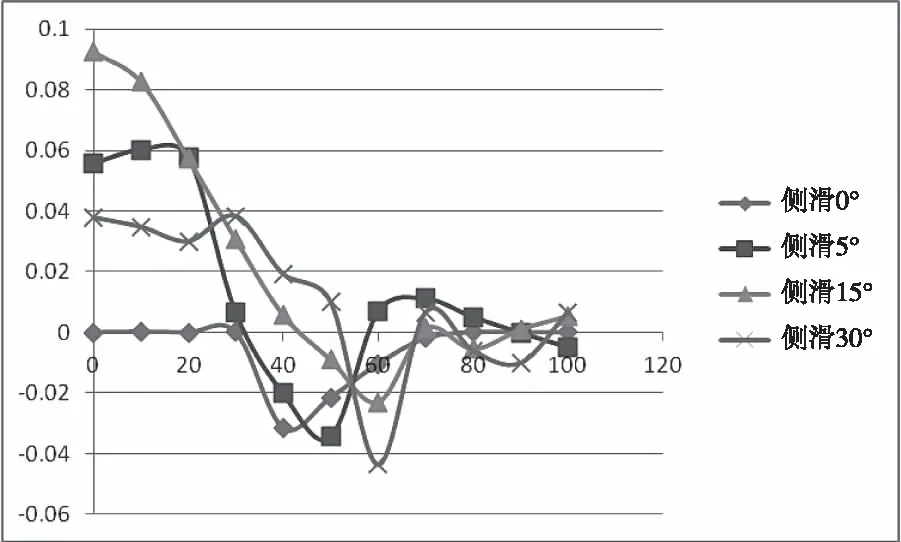
图5 偏航力矩系数～迎角曲线

图6 滚转力矩系数～迎角曲线

表1 大气参数

3.3 风场模型

风场方向的定义如图7所示。

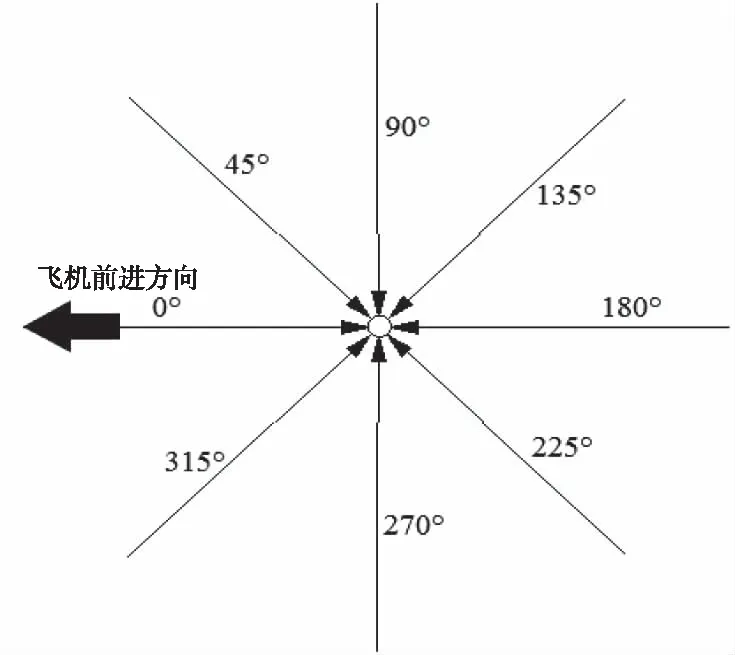
图7 风场方向示意图

风场方向说明如下：风速度方向为0°，即风速矢量指向地面系x轴正方向，风从载机正前方吹来。

常用风场模型[7]风速大小如下图所示：

从上图可以看出，风速和风切变随高度先增大后减小，但是由于无伞空投物品的投放高度较低、风速变化不大，不考虑垂直风速和垂直风切变，只考虑水平风速和水平风切变对空投物品下落过程的影响。在仿真过程中给出平均风速，并根据空投物品当前高度插值获取当前位置风速进行仿真计算[8-10]。

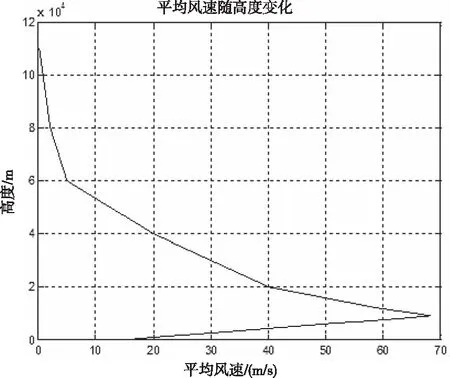
图8 平均风速随高度变化

图9 风切变随高度变化

3.4 其它模型

1)大气密度计算模型

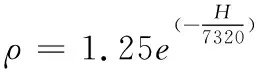
(6)

式中，ρ表示大气密度，H表示空投物品的飞行高度。

2)声速计算模型

(7)

式中，a0表示当前声速。

3)重力计算模型

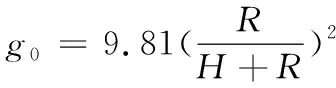
(8)

式中，g0表示空投物品当前受到的地球引力加速度大小，R表示地球半径。

4 空投仿真及落点精度敏感性分析

敏感性是指一个或多个因素由于自身变化而造成项目指标的变化，反应了项目指标对这些影响因素的敏感性，亦可表述为这些因素对项目的影响程度或重要程度。由于对空投物下落情况造成影响的因素众多，为综合分析每个因素的影响程度，先对空投物品落点进行局部敏感性分析，即每次只改变空投物品初始状态的一个属性，研究其初始值改变对落点的影响，待所有的初始状态属性分析完毕，对空投物品落点精度进行全局敏感性综合分析。

4.1 落点精度影响因素分析

空投物品落点精度影响因素分析即找出所有影响空投物品落点精度的因素，该部分研究内容多见于多属性决策研究，即在进行多属性决策时需要获取所有的影响因子，充分考虑每个影响因子的影响来进行决策。

本文采用层次分析法，将问题进行层次分解，将一个综合性因素分解成几个子因素，再将子因素进行分解，直到不能分解为止，则最底层的因素即为全部的影响因素。影响因素主要涉及三个方面：外部环境、出舱状态和自身质量特性与气动特性，对空投物品落点精度运用层次分析法得到的影响因素见表2。

表2 空投落点精度影响因素表

4.2 单因素仿真局部敏感性分析

通过对表1中27个影响因素进行单因素仿真，可以得出每个影响因素在不同误差下对落点X轴距离、落点Y轴距离、下落速度及下落时间的影响程度。在此以投放高度为例，对其进行局部敏感性分析，研究投放高度误差在-10%～10%情况下对落点精度的影响程度。仿真条件设置如下：投放速度70m/s，投放高度200m，投放倾角0°，投放偏角0°，弹射速度0m/s，弹射角度0°，风速大小0m/s，风向0°，仿真结果如图10和图11所示。

图10 空投物品下落轨迹

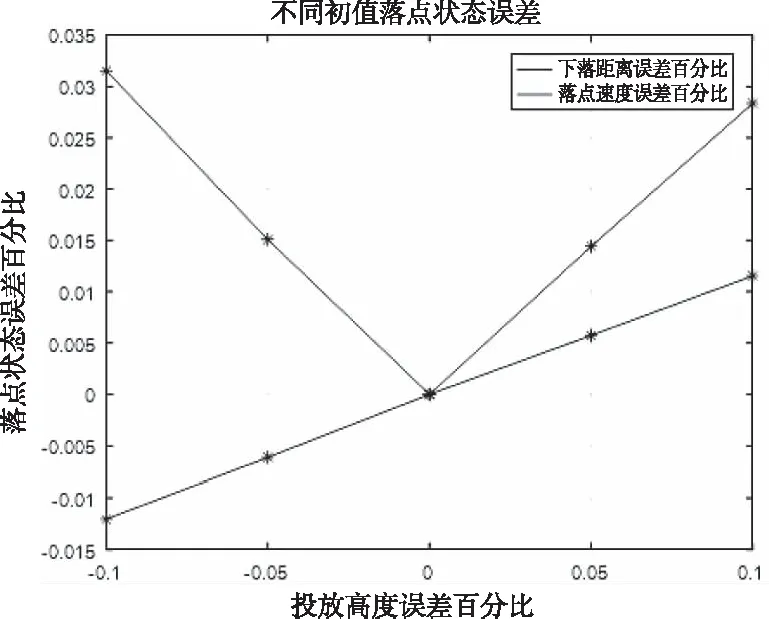
图11 不同投放高度误差下落点距离误差百分比

落点数据信息见表3。投放高度在-10%、-5%、0、5%、10%误差情况下，X轴上的下落距离变化明显，高度每增加10m，落点X轴距离增加5m左右，下落时间和落地速度也有少量增加。

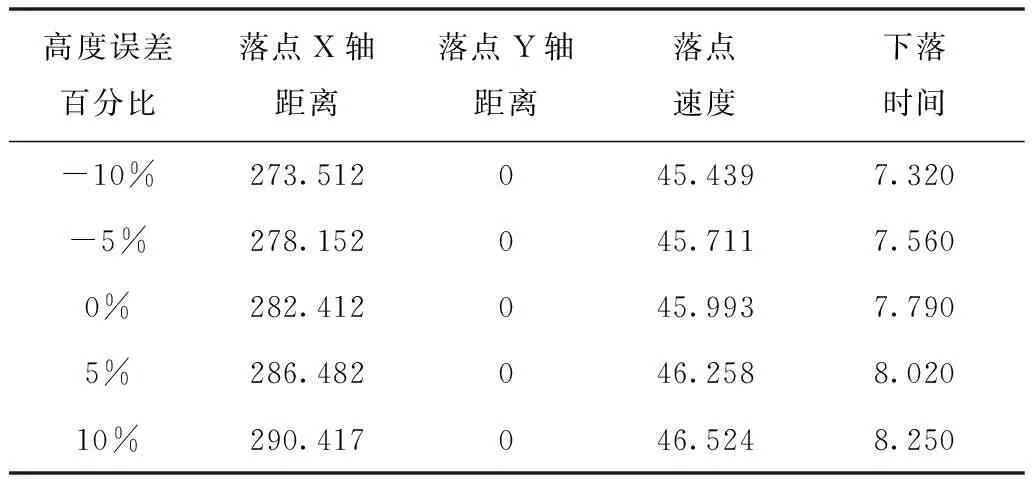
表3 空投物品落点状态表

4.3 大规模综合仿真全局敏感性分析

为分析空投物品落点精度全局敏感性，对空投物品落点精度影响因素除去外部环境因素，在一定范围内选取多个不同初值和不同误差做大规模仿真计算，分析所有投放条件下的落点误差距离，仿真计算条件设置如下：

投放高度(m)：50、100、150、200、250

投放速度(m/s)：50、60、70、80、90

投放倾角(°)：-5、0、5、10、15

投放偏角(°)：-20、-10、0、10、20

弹射速度(m/s)：2、6、10

弹射角度(°)：-10、0、10

以及空投物品自身特性影响因素包括：气动系数、质量、转动惯量、质心位置、气动特征面积和气动特征长度。

针对上述所有投放条件情况，在给定误差-10%、-5%、5%、10%的情况下分析落点距离误差，对每个影响因素将产生5*5*5*5*3*3*4=22500条数据，并对每个误差状态取落点距离误差的均值，如图12所示。图中纵轴表示影响因素的敏感性排序，从前到后字母含义为：质心y轴偏移、投放速度、质量、阻力系数、气动特征面积、投放高度、投放偏角、投放倾角、弹射速度、弹射角度、质心x轴偏移、气动长度、升力系数、侧力系数、滚转力矩系数、偏航力矩系数、俯仰力矩系数、x轴转动惯量、y轴转动惯量和z轴转动惯量，共计20个影响因素，其中质心偏移的误差百分比为-10%，-20%，-30%，-40%，其它影响因素误差百分比为-10%，-5%，5%，10%，分别对应图12中的误差百分比1，2，3，4。

图12 空投物品落点误差距离均值

4.4 敏感性分析总结

对落点纵向距离影响较大的因素有：投放高度，投放速度，投放倾角，质量，质心y轴偏移，气动阻力系数，气动特征面积，风场；对落点横向距离影响较大的因素有：投放偏角，弹射速度，风场。其余因素对落点精度的影响可忽略不计。

4.5 空投任务系统的建议

4.5.1 高精度投放建议

1)保证投放状态的精度，即保证载机显示的载机状态精度很高，包括载机的高度、速度、航迹倾角和航迹偏角。

2)在满足载机飞行条件的情况下，降低投放高度，可减小因高度计算误差带来的影响，此外，高度越低，空投物品的落地速度越小，有利于空投物品的安全。

3)空投物品的落点精度不受弹射角度的影响，所以尽量水平投放，减小投放难度和投放人为误差。

4.5.2 空投物品外形设计建议

1)在不减小空投物品质量的情况下，增大空投物品的气动特征面积或气动长度，有利于减小空投物品的落点速度。不建议减小空投物品的质量，因为减小质量会降低空投包的抗干扰能力。

2)增大空投物品的阻力系数，有利于减小空投物品的落点速度，如增加几片水平安置的小翼。

3)空投物品的质心向下偏移越多，越有利于空投物品的飞行稳定。由于装填物资时很难保证空投包的质心与形心重合，质心偏移较少会造成空投物品飞行过程不稳定，姿态容易发生抖动。因此可以在空投外形设计制造时人为增大空投物品下半部分质量。

5 空投仿真及载机安全性分析

根据敏感性分析结果可知，影响空投物品横向运动的因素主要包括载机偏航角、弹射速度和风场，由于单独改变偏航角不会改变空投物品与载机的相对运动，而弹射速度会使空投物品远离载机，所以安全性分析中主要考虑风场对载机安全性的影响。

5.1 安全性分析

载机安全性分析即分析空投物品投出后是否会碰撞到载机，以及不同风场状态对载机航向角的约束范围。设置式(5)中l+D=10。安全性分析时只考虑载机和空投物品形心距离是否小于5米。

仿真条件：投放速度70m/s，投放高度200m，投放倾角0°，投放偏角0°，投放弹射速度5m/s，投放弹射角度0°，风速大小5～20m/s，风向0～360°。不同风速下载机与空投物品的最小距离如图13示，危险风向范围见表4。

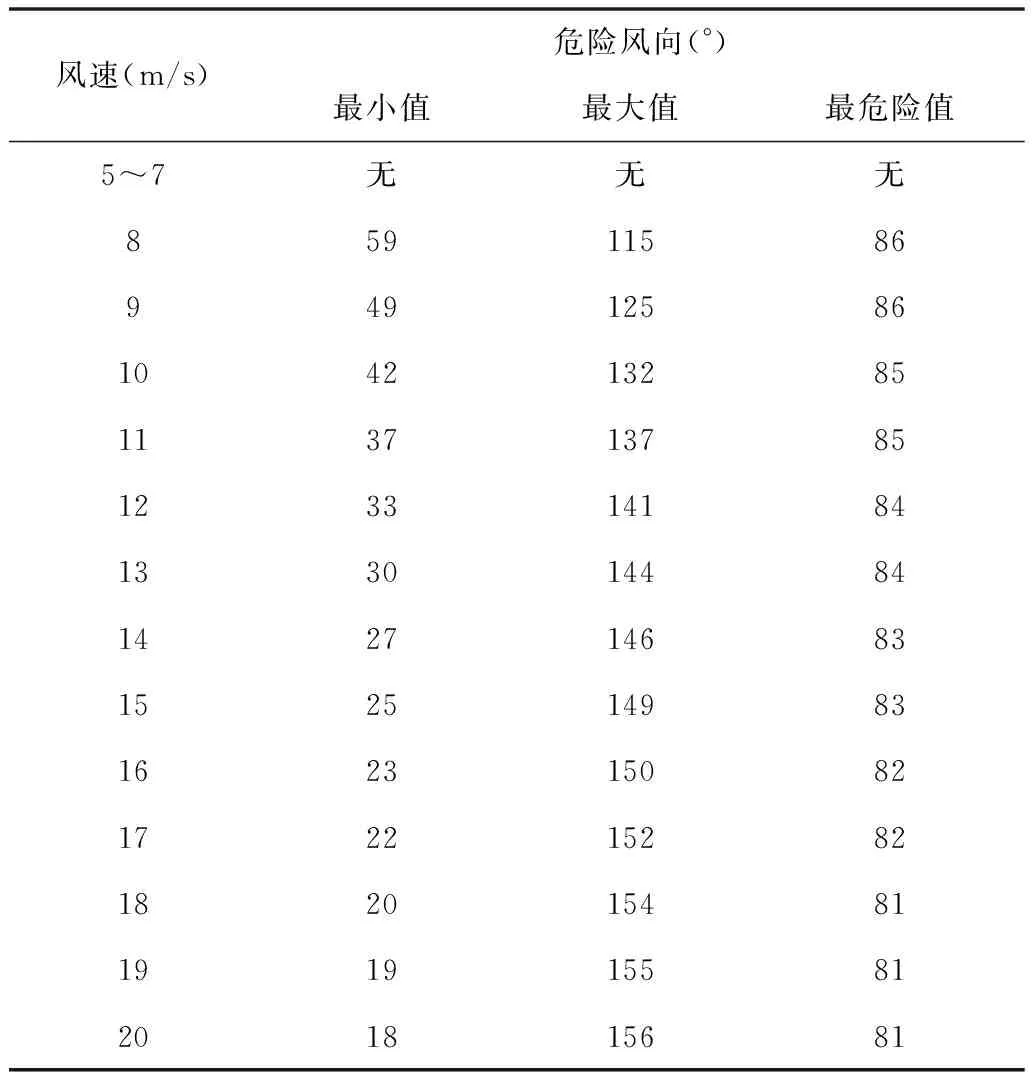
表4 弹射速度5m/s危险风向范围表

图13 弹射速度5m/s载机与空投物品最小距离随风向变化曲线

弹射速度为5m/s时，能抵抗7m/s及以下风场干扰，即当风速在7m/s以下时，不管风向如何，空投物品以5m/s或更大的速度弹出，均不会碰撞到载机。当风速为10m/s时，危险风向范围为42°～132°，最危险值为85°，在进行空投时需调整载机飞行航向角，从而改变风场的相对位置，确保空投物品不会因风场而碰撞载机。风速越大，危险风向的范围就越大，对载机的航向角约束也越大。同时，空投物品的弹射速度越大，抗风场干扰能力越强。