基于同态滤波的平面视觉图像色彩增强算法

李连志，邢 川

(河北科技大学，河北 石家庄 050000)

1 引言

图像在成像过程中，会因自然环境因素或人为因素导致出现缺乏光照、视觉效果不佳以及图像清晰度不高等情况，而阴影图像、弱光图像的处理一直是图像处理中难点之一。解决上述问题不仅具有重要的理论意义，而且在实际应用中也有很大应用前景，例如航空影像、遥感影像、视频监控中的乌云影像等。合理运用图像增强技术，可以从根本上解决图像存在的质量问题，令图像视觉效果更清楚，更能体现图像的细节。

王建卫[1]为了解决低照度彩色图像边界提取不完整的问题，依据点处理和颜色空间变换理论，提出了应用非线性函数变换方法处理HSI颜色模型的强度分量彩色图像增强方法。设计非线性函数变换进行彩色图像增强计算，并分析了算法中RGB和HSI颜色模型的转换强度，进行分量计算，获取增强后图像。赵军辉[2]等人提出基于Lab色彩空间和色调映射的Retinex图像对比增强算法。首先，在Lab色彩空间中将一个低对比度的输入图像分解成亮度和色度分量，并使用自适应双边滤波估计照明的强度，以便根据亮度和颜色值来考虑合适的相邻像素。然后利用基于抛物线的色调映射函数来提高估计光照图像的对比度。最后，将加强的亮度和原始色度结合在一起，产生一个增强彩色输出图像。

虽然上述方法都能使图像色彩增强，但是各色块间像素分布依旧不够均衡，人眼视觉舒适度较差，因此，为了能够获取出较好的视觉效果，将图像色彩空间从RGB转换为HSV，并对转换后图像进行亮度分量增强；根据需要处理图像的构成因素，利用压缩低频、提升高频法，获取出经同态滤波处理后的视觉效果图像，构建巴特沃思型的同态滤波器；因为在计算同态滤波过程中需要同时在不相同的图像块中单独运行，所以导致图像边缘处会形成不同样式的块效应，并会有图像像素越平滑，块效应越显著的情况，因此，提出基于重叠块的块效应去除方法，实现平面视觉图像色彩增强。

2 空间转换及亮度增强

2.1 色彩空间转换

RGB颜色模型由R、G和B原色组成，虽然RGB模型有一个舒适的色彩显示效果，但是模型中两个相似颜色值之间的差异太大，导致计算结果不完全一致，修改后模型三个分量之间的相关性很高。如果其中一个组件值更改，则其它两个组件值也更改。与RGB模型不同，HSV(Hue， Saturation， Value)是一种基于人眼视觉系统的颜色模型。HSV模型主要有两点明显的特征，其一是V分量的取值变化和图像整体的色彩信息没有关联；其二是H或S分量与人眼视觉所感受颜色的方法是一样的。根据这两点特征，即可进一步得知HSV色彩空间模型比RGB模型更适用于彩色图像处理算法，因此，在处理图像前，首先将需要处理图像的色彩空间由RGB模式转换为HSV模式[3]。

假设(r，g，b)为一个颜色的红、绿、蓝坐标，要得到HSV空间中的(h，s，v)值，那么转换公式就可以写为

υ=max{r，g，b}

(1)

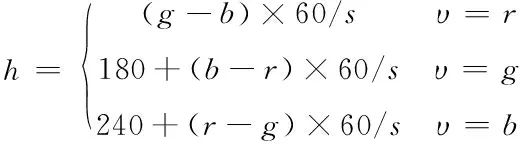
(2)

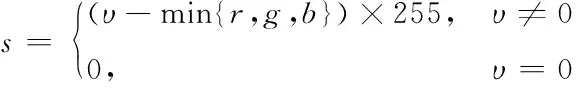
(3)

当给定(h，s，v)值，对应的(r，g，b)三原色为

(r，g，b)=(r′+λ，g′+λ，b′+λ)

(4)

其中，λ=υ-c。

2.2 亮度分量增强

由于在运用同态滤波算法对图像进行色彩增强处理之前，需要将图像预处理，获取出与原图相比较亮的图像，因此，利用全局直方图和局部直方图均衡化方法，令图像灰度值达到分布均匀效果，然后运用灰度映射扩展图像中像素值的动态范围。但预处理过程中，容易发生颜色失真，产生新噪声的情况，并具有难以达到满意效果、计算量过多以及形成马赛克效应等缺点[4]。

为了解决上述问题，将图像分块，然后将基于DCT变换的同态滤波器分为所使用的每个子图像[5]。将待处理的图像分为8×8个子图像，图像块为8×8二维矩阵f(m，n)，其中0≤m≤7，0≤n≤7，则f(m，n)的DCT变换定义为

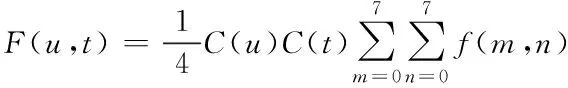
(5)

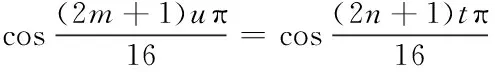
(6)

其中，0≤u≤7，0≤t≤7。

(7)

经过色彩空间转换和亮度分量增强可以提取出较亮的图像，使图像灰度值的分布更加均匀。

3 基于DCT变换的同态滤波

一般情况下常用的同态滤波算法有高斯型与指数型，这两种滤波算法的不同之处在于处理图像时传递函数的取值，根据计算选取出适用于解决图像问题的传递函数，就可以直接让图像达到最满意的效果，如果不是最合适的函数，那么便可获取出不同的增强效果，直至经过调整令其达到最佳效果。然而在具体计算过程中，传递函数的控制参数太多，需要经过大量计算来确定最终可以达到满意效果的传递函数。因此，实用性不强。

3.1 构建同态滤波模型

鉴于现有方法存在的问题，根据构成图像的光学特征得知，图像由自然光照度分量i(x，y)和图中主要目标的反射分量r(x，y)构成，根据其组成条件[6]，数学模型可以表示为

f(x，y)=i(x，y)·r(x，y)

(8)

一般情况下，照度分量i(x，y)可以充分反射出光照条件是好或是坏，如果照度分量呈缓慢变化，那么频谱就会落在低频区域；而反射分量r(x，y)则是主要映射图像目标物件的内容细节，该分量图像中的频谱区域为高频部分[7]。根据上述分布情况，只需要在f(x，y)中将照度分量i(x，y)和反射分量r(x，y)划分开，并在此基础上采用压缩图像低频，提高图像高频的方法，就可以实现降低图像中亮度分量，使图像视觉效果更清晰。

针对式(8)左右两侧，计算选取出具有代表性的对数，这样就可以将乘法运算转换为加减运算组合，便有

lnf(x，y)=lni(x，y)+lnr(x，y)

(9)

根据上式计算结果，利用DCT变换代替传统同态滤波中的傅里叶变换[8]，经过对式(9)变换后即可得出下式

F(u，t)=I(u，t)+R(u，t)

(10)

其中

F(u，t)=DCT[lnf(x，y)]

I(u，t)=DCT[lni(x，y)]

R(u，t)=DCT[lnr(x，y)]

(11)

用同态滤波函数H(u，t)来处理上式中的F(u，t)，得出

S(u，t)=H(u，t)F(u，t)=H(u，t)I(u，t)+H(u，t)R(u，t)

(12)

经滤波处理后，再经过逆DCT变换(IDCT)，得到

s(x，y)=IDCT[H(u，t)F(u，t)]

=IDCT[H(u，t)I(u，t)]+IDCT[H(u，t)R(u，t)]

(13)

经过DCT变换计算后，针对式(13)进行指数变换，这样即可获取出滤波后的图像

g(x，y)=es(x，y)

(14)

通过DCT变换运算的均匀滤波算法，选取图像展开的对数，得出对数结果后实施DCT变换处理，其次，在变换域中对适合改进的图像进行滤波操作，可得出基于反向和指数变换的同态滤波器。

3.2 同态滤波器

在同态滤波计算过程中，同态滤波函数H(u，t)的取值结果会直接影响最后变换计算的结果是否精准。为了能从根本上缓解图像因光照环境导致的图像色彩不均匀或是图像视觉效果失真等情况，应该降低I(u，t)频率分量，同理为了更加凸显图像细节，提高图像中目标物的对比度，则需要提高R(u，t)频率分量。通过上述分析，再融合同态滤波函数的特点，设计巴特沃思型的同态滤波器，其中表达式为

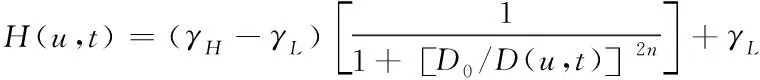
(15)

其中，γL<1，γH>1；L代表滤波器的平滑阶数；D0代表停止过滤的频率；D(u，t)代表点(u，t)到DCT变换最初点的距离，其计算公式如下

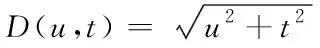
(16)

4 基于重叠块的块效应去除方法

4.1 基于HVS的块效应可见度函数

在使用消除块原理的过程中，需结合视觉系统特征。曾有相关研究表明：部分空间活动及图像光亮程度可遮掩消除块效应，但在纹理部分，区块效应的可见度略低。因此，在局部背景亮度较高的区域，块效应的可见度相对较低。如图1所示，块与相邻块之间的块边界被理解为块边界的局部区域[9]。图1为水平相邻块组成的新块。

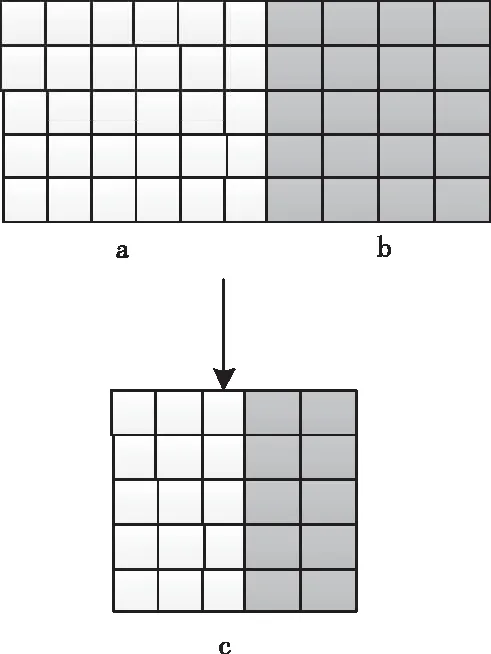
图1 水平相邻块组成新块示意图

块效应可以通过垂直和局部空间活动来掩盖，基于同态滤波计算结果定义水平和垂直函数

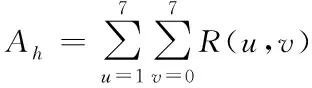
(17)

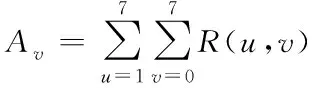
(18)

其中，将Ah和Av描述为块c在水平或是垂直方向的特征活动性，这样根据其特性即可令R(u，v)代表块c模型中反映局部活动性的剩余块在DCT域中的取值。

一般情况下，对于存在水平方向中的块效应来说，垂直方向的活动是导致块效应隐蔽的主要原因，因此，可根据下式判定垂直或水平方向块效应的所有活动性

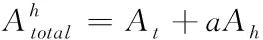
(19)

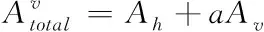
(20)

因此，定义了空间频率活动对水平方向阻滞效应的掩蔽函数Mh，见式(21)

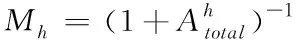
(21)

根据上式计算结果，即可写出亮度均值的计算式

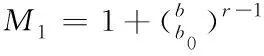
(22)

根据上述计算结果得知，如果图像空间活动性的频率不能达到掩盖函数的正常取值范围，那么图像中的方块效应也会随之产生可见度变化，掩盖函数取值越小，块效应的可见度就会呈现出越低的情况，这样就可以进一步判定，垂直方向的块效应可见度函数ηv

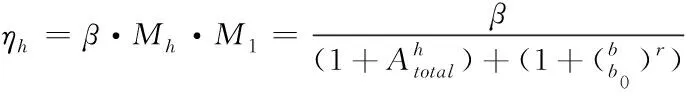
(23)

4.2 图像色彩增强的块效应去除

当块c的ηh大于等于阈值T时，对块c进行边缘检测，边缘检测的目的是防止边缘被视为块效应。为了能够有效防止出现忽略图像边缘像素的情况，导致在后期处理过程中图像呈现出视觉效果不清晰的情况，提出一种新的图像边缘检测方法，并且当像素转换块c满足于下列计算条件时，就有

c(i，j)-c(i，j+1)≤c(i，4)-c(i，5)

(24)

c(i，4)-c(i，5)≤2QP

(25)

其中，i=0，1…，7，j=0，1，…，6。

根据下述两点条件，可以认为转换块中没有边。

条件一：为了避免转换过程中出现较大的效应误差，利用空间频率结果将像素之间的差异控制在块边界像素可接受范围内[10]。

条件二：防止边缘仅出现在块边界上。

为了消除平滑块的块效应，用线性函数代替阶跃函数。如果用线性函数代替梯形函数，那么这些系数的取值在本质上就会发生变化，但只运用部分转换块信息的话，就会忽略图像块中左右两侧部分的信息，进而形成新的块效应。通过块a和块b左右局部信息，改变C(0，1)，C(0，3)C(0，5)和C(0，7)的值，从而改变β的值，最后再用线性函数代替阶跃函数去除块效应。从而完成对平面视觉图像整体色彩的增强。

5 仿真研究

为了验证所提算法的有效性，运用MATLAB软件进行仿真，并将所提算法的仿真结果与文献[1]、[2]方法进行比较。

5.1 主观质量评价

在实验过程中，将块效应可见性函数的阈值设置为0.02。图2(a)代表原始图像，图2(b)代表块效应严重的JPEG解码图像，图2(c)代表本文算法处理的重建图像。

图2 效果图像图

分析图2可知，从视觉角度出发，运用所提算法增强后的效果图，不论是从图像色彩还是图像块效应方面均得到了有效改善，图2(b)中图像具有明显的块效应，图像模糊、边缘信息严重丢失，不能达到更清晰的效果。这是由于所提算法为了能够有效防止出现忽略图像边缘像素导致形成块效应的问题，提出了一种图像边缘检测方法，该方法可以将图像像素之间的差异控制在块边界像素可接受范围内，从而有效抑制块效应的产生。

5.2 客观质量评价

为了客观地测量和评价算法性能，采用信噪比(SNR)对处理后的图像质量进行测量，结果如表1所示。

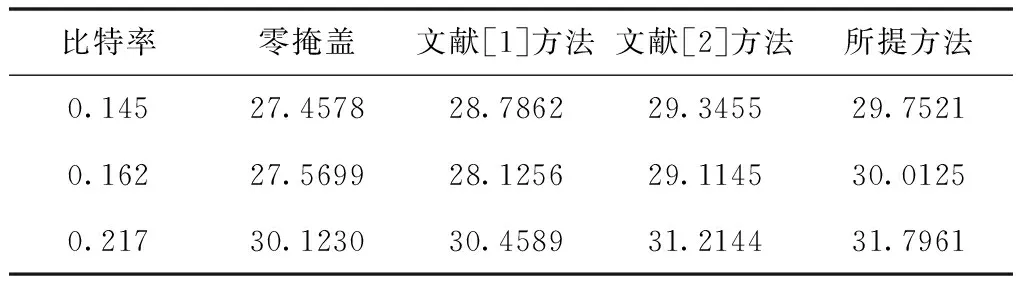
表1 不同比特率下的信噪比

从表中可以看出，所提方法在不同比特率下的信噪比均高于文献[1]方法和文献[2]方法，说明提出的算法可以有效地消除图像的块效应，保护图像边缘信息，增强了图像中因光照环境影响导致的图像色彩。

为了进一步验证所提方法的图像色彩增强效果，建立图像客观质量综合评价准则，运用该准则评价不同方法，将综合评价准则定义为CAC(Comprehensive Assessment Criteria Index)

CAC=EmNnCp

(26)

其中，Em表示图像结构相似性测度；Nn表示归一化灰度差；Cp表示色彩加权还原度。CAC取值越大，说明图像色彩增强效果更好，不同方法的CAC值对比结果见表2。

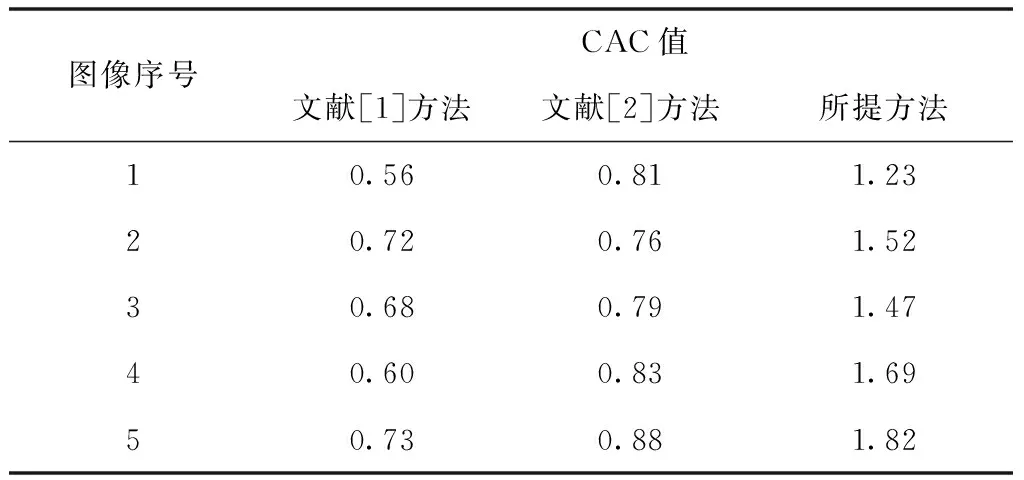
表2 不同方法CAC值对比

分析表2可知，采用所提方法对不同图像色彩进行增强之后，所得的CAC值均高于1，该方法的CAC值明显高于文献[1]方法和文献[2]方法，说明所提方法的图像增强效果更好，进一步验证了该方法的优势性。

以上实验结果说明同态滤波技术是在该研究领域中较为有效的色彩光照图像增强法，该方法可以避免图像失真的问题，并且可以做到在保持原有图像色彩的基础上，增强色彩暗区的细节，解决因光照环境导致的色彩分布不均或是过暗的问题。

6 结论

图像成像过程中，因自然或人为因素导致的图像失真或色彩变暗会影响视觉效果，该问题已经成为该研究领域中需要解决的主要问题之一，因此，提出基于同态滤波的平面视觉图像色彩增强算法。根据色彩空间特征，将RGB转换为HSV形式，以便于得出效果最佳的处理图像效果，经过同态滤波计算构建出巴特沃思型的同态滤波器，利用可见度函数对图像中存有的块效应去除，获取出色彩增强后的图像。虽然本文算法最后可以实现图像色彩增强目的，但由于去除块效应计算中，可见度函数结果阈值需要精准且有效，导致需要针对阈值结果反复，下一步将主要针对计算过程进行优化。