基于反距离权值的终端区航迹预测方法仿真

李 沐

(中国民航大学，天津 300300)

1 引言

终端区域是空管系统中最复杂、管制员压力最大的区域之一。与巡航的飞行相比，航空器在终端区域内的飞行更易受天气、飞行冲突，流量异常等状况的影响，飞行路线更加不确定，有时需要依靠管制员的指令脱离固定的进离场航线飞行。终端区包含大量航迹数据，这些数据中蕴含管制员的意图，航空器的性能以及飞行员的操作习惯等诸多不易察觉的因素，通过数据挖掘的方法可以对航迹进行精确预测。而终端区内的航迹预测可以为管制员提供航空器的飞行辅助信息，为进一步实现空管自动化提供先决条件。

国内外主要有两类航迹预测方法，第一类基于航空器动力学与运动学模型[1-3]。该类方法通过对航空器的飞行环境进行推测，考虑温度、风向和风速等因素对航迹可能产生的影响，根据航空器飞行时所处的不同阶段建立不同的空气动力学模型。此类方法在面对不同机场的终端区时很难构建符合实际的模型。第二类方法是基于数据挖掘的航迹预测。王静、张建伟[4]等利用遗传算法挖掘历史数据，通过基因表达式编程挖掘频繁函数集建立模型，该模型利用遗传算法对历史飞行数据进行操作，挖掘出数据集中相对应的函数关系集合，用较好的函数模型对未来航迹进行预测。Gariel M[5]等利用聚类方法对航迹数据分类，在去除偏离航迹后提取典型航迹，然而该方法航迹的预测精度较低。Song Y[6]等人通过对不同航迹的历史飞行数据进行分析，并基于分析得出的聚类结果，得到精度更高的预测模型。上述航迹预测方法大多适用于时间较长，距离较远的航迹预测，在时间跨度较短，情况复杂的终端区时很难做到较为精准地预测。

针对以上问题，本文提出了一种基于反距离权值的终端区航迹预测方法，首先通过聚类算法挖掘出航迹分类信息，结合随机森林模型给出航迹分类预测模型，然后将分类标签结合插值后的历史航迹数据给出典型航迹，最后通过反距离权值法求得更加精准的预测航迹。

2 航迹数据预处理

首先进行数据清洗，整理后得到可用数据，然后利用DTW算法(Dynamic Time Warping)计算航迹间距离作为航迹聚类中各航迹间的距离度量，最后通过聚类算法将终端区域内具有相似时空特征的航迹聚类，得到不同的航迹标签，为航迹预测提供分类基础。

2.1 数据整理与压缩

本文数据来源于广播式自动相关监视(Automatic Dependent Surveillance Broadcast，ADS-B)。由于地形遮挡，网络波动等问题，真实航迹与获取数据之间可能存在偏差，主要问题分为以下3种：

1)数据存在丢包现象，其表现为个别航迹点的缺失或中段部分航迹数据的缺失。此外，部分航迹的起点在数据开始记录时不在终端区的边缘，即该航班在开始记录数据之前已经飞入终端区，此类航迹归为不完整航迹。对于航迹点缺失较少的情况可以插值补全，对于起点不再终端区边缘或缺失较多数据点的航迹，应进行去除。

2)数据存在重复项，重复数据在增大了计算量的同时也会影响后期对数据的处理，应去除含有完全相同信息的数据项。

3)存在干扰航迹，部分航班在同一天的飞行时间可能会执行多次航班任务，存在同一航班号对应多条航迹的现象，因此在分离不同航迹时需要在考虑航班号的同时考虑数据点之间的时间间隔，将同一航班号的不同时间段的航迹区分开，排除干扰。

由于数据量大，需要对数据进行适当的压缩，去除包含冗余信息的数据项，只留下能够体现航迹特征的数据。本文利用Sliding Window算法[7]压缩航迹数据。所有留下的特征点形成压缩后的航迹。

经过以上几步的数据预处理得到可以用于航迹聚类和航迹插值的数据。

2.2 航迹聚类

2.2.1 航迹间距离

聚类是一种无监督学习，通过一定的规则在无先验知识的情况下通过定义的相似性将数据分为不同类别的过程。在二维平面问题中，通常用欧式距离定义点与点之间的距离。不同航迹由数目不同的数据点构成，无法通过比较对应点的欧式距离来表示航迹间的距离，因此这里引入动态时间规整算法(Dynamic Time Warping， DTW)计算航迹间的距离[8]。该算法通过动态规划寻找两个不同长度序列之间的最优映射，进而计算两个序列之间的距离。

定义历史航迹集

C={C1，C2，…，Ci，…，Cj，…，CN}

(1)

式中，Ci和Cj分别代表第i条和第j条历史航迹；假设Ci和Cj分别由m和n个数据点组成，则

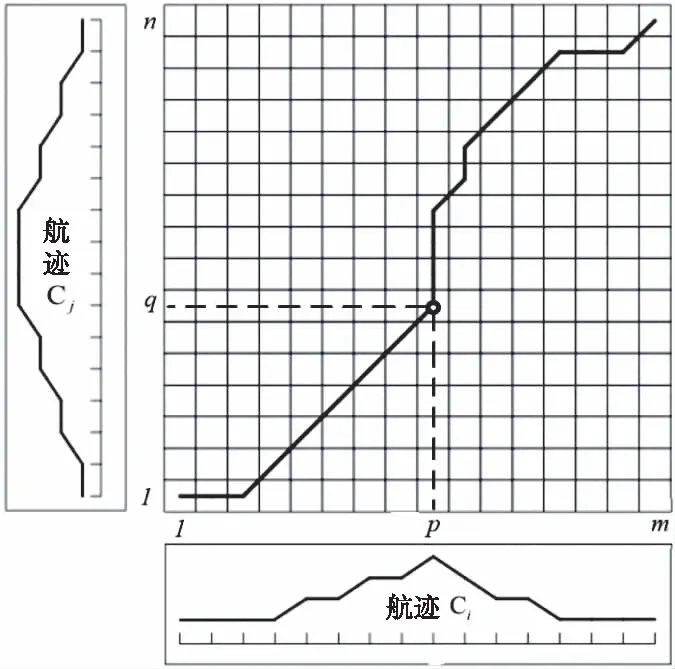
图1 动态时间规划过程示意图

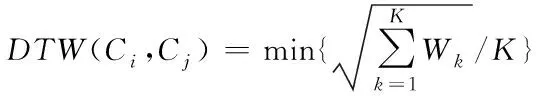
(2)

定义累加距离D(p，q)，从(1，1)点开始匹配序列Ci和Cj，每到一个点，之前所有点的计算距离都会累加。

当匹配点(p，q)到达终点(m，n)后，累加距离D(m，n)为Ci和Cj之间的距离，记为γ(i，j)。

由于DTW算法用时较长，本文将采用效率更高的FastDTW算法[9]，该算法综合限制搜索空间和数据抽象两种较为有效的加速方法提高DTW算法的效率。经过计算，历史航迹集trajprek中各航迹间距离可表示为如下矩阵

(3)

式中，R为N×N的对称矩阵，矩阵对角线为航迹与自身的距离，均为0。此航迹距离矩阵将用于航迹聚类时的相似度计算。

2.2.2 航迹聚类

由于航迹数量较大，若直接计算所有航迹间距离耗时较长，所以先通过均值漂移聚类算法[10]区分不同入口处的航迹簇，再分别对每一簇航迹进行DBSCAN聚类(Density-Based Spatial Clustering of Applications with Noise)可以提高计算效率。

对航迹数据集的相似度结果进行整合，计算数据集自然簇的均值xi，进而对航迹数据集中的数值型数据进行聚类处理

(4)

以均值xi代表该自然簇，得到新的航迹数据集，采用SINGLE算法对新数据集进行聚类，对k个簇进行合并，计算自然簇质心的初步位置。

由于航迹数据集属于局部信息，自然簇质心的真实位置相对于初始位置，会发生一定的偏离。因此必须对自然簇质心的初始位置进行偏差修正，以获取精确度的质心的位置。

基于密度空间的数据聚类方法DBSCAN通过不断扩张其中心区域[11]，不断增加区域内所包含的对象的数目。该聚类可由其内部任何一个核心对象所唯一确定，当密度足够大时，相邻区域可通过互相连接的方式在包含噪声干扰的空间数据库中发现任意形状的类簇。该方法在面对包含噪声和异常的空间数据时，处理较为有效。

在得到不同入口点的航迹簇后，针对每一簇航迹，利用1.2.1中航迹间距离矩阵作为航迹间距离度量进行DBSCAN聚类，得到各航迹簇的不同聚类集合。经过DBSCAN聚类得到历史航迹数据的聚类类别，即排除噪声航迹后，每条航迹的分类标签。

2.3 航迹插值

为了更好地利用时间信息串联各航迹数据，需要对在时间线上缺失的数据进行插值。经过线性插值后的数据在时间层面上有相似的长度，保证了把每条航迹的第1个点记为零时刻时，每隔相同的时间段都有相应的航迹数据。将经过插值后的数据集记为Citp。为了在短时间内进行多次预测，先将插值后的数据按照时间进行分段处理。以Δt为时间间隔切分航迹数据集，保证每一段包含相同数目的数据点。

3 航迹预测算法

通过上一节航迹聚类的方法得到航迹数据的分类标签。本节通过将数据输入随机森林模型得到航迹数据的分类预测，通过预测分类的标签与经过插值的历史航迹结合，得到典型航迹，再通过反距离权值[12]法优化典型航迹，得到最终的预测航迹。

随机森林是一个由多个决策树组成的分类算法，它的分类输出标准是多个决策树输出分类标签的相同的大多数，是集成学习中应用较为成功的算法。在随机森林的构建过程中包含两部分，一部分在训练数据中采用有放回的方式对等量的训练样本进行随机采样，另一部分是在建立决策树时对属性的特征进行随机选取。这种随机选取样本以及随机选取特征的方式可以在一定程度上降低决策树之间的相关性，可以在模型的准确性上有进一步的提高。

随机森林分为训练和测试两个部分，将历史航迹数据集分为两个部分，训练集和测试集，训练时输入训练集航迹经度，纬度数据以及每条航迹数据所在分类标签，输出为航迹预测分类标签，在训练过后得到符合当下情况的随机森林模型，再输入测试集航迹数据，得到测试集预测分类标签。

将Citp按照时间间隔Δt分段，第k段航迹数据集记为CΔtk，第k段航迹预测分类为clusterk，测试航迹记为trajt，第k段测试航迹记为trajtk，第k段典型航迹数据集记为Trajtypk，包含的航迹数目记为l，第k段典型航迹记为trajtypk，第k段预测航迹记为trajprek。

具体的航迹预测流程如下：

将第k段测试航迹trajtk输入训练好的随机森林模型，输出测试航迹的分类标签clusterk。

找到第k段航迹数据集CΔtk中属于clusterk类的航迹数据集，选取其中与测试航迹trajtk距离最近的l条航迹形成典型航迹数据集Trajtypk，Trajtypk包含这l条航迹所有时间段的航迹数据。

在第k+1段求这l条航迹的平均航迹得到第k+1段的典型航迹trajtypk+1。

将第k+1段典型航迹trajtypk+1作为观测航迹，利用反距离权值法重新分配Trajtypk中所有航迹数据点的权值。

利用新的权值与典型航迹数据集Trajtypk中在第k+1段所有航迹数据求加权平均得到第k+1段trajprek+1。

4 实验验证与分析

选取天津滨海国际机场终端区域，数据纬度区间为北纬38°至北纬40°，经度区间为东经115°至东经119°，2017年5月4日至30日共3074条历史航迹数据进行航迹预测。

4.1 聚类结果

针对所有航迹入口点进行均值漂移聚类，经过反复测试，设置bandwidth为0.152，每个圆内包含的点数为30，每个聚类内的数据点数目需大于20个。结果如图2a所示，该算法将所有航迹入口处的数据分为7类。

选取航迹簇1中的航迹进行DBSCAN聚类，结果如图2b)所示，图中不同颜色的线分别代表同一航迹簇下3类不同的聚类，从图中可以明显地看出不同机场跑道入口处没有出现分类不正确的情况，因此聚类效果是比较理想的，可以作为航迹预测分类的标准。

图2 航迹聚类

4.2 航迹预测结果

将插值时间选为每1秒进行一次插值，Δt为60秒，l为10。选取测试集中的某条航迹，输入航迹预测模型，将得到的典型航迹、预测航迹与实际航迹作对比。

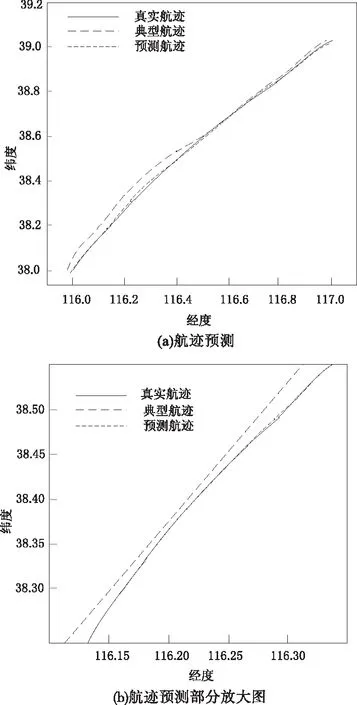
图3 航迹预测

图中红色线段为真实航迹，绿色线段为典型航迹，蓝色线段为预测航迹。在整体航迹的预测过程中，典型航迹与实际航迹的距离较大，而通过图3b也可以看出典型航迹只能大致给出航迹的走势，但在改变权重之后，预测航迹与实际航迹非常贴合。具体误差值如图4所示。预测航迹每秒与实际航迹间距离差不超过1.1km。而典型航迹的差距较大，所以通过反距离权值重新分配权重方法是有效的。

图4 预测航迹与典型航迹误差比较

5 结束语

本文基于历史航迹数据集研究了终端区域航迹预测问题，提出了一种结合随机森林和反距离权值的航迹预测算法，首先阐明了通过聚类算法获得航迹分类标签的过程，其次将插值后的数据按照时间分段，通过随机森林模型与插值后的历史航迹数据相结合生成典型航迹，采用反距离权值法将典型航迹生成预测航迹，实验验证表明当数据量较大时，这种针对终端区的航迹预测方法效果较为理想。