带状态观测器的船舶路径跟踪预测滑模控制
2021-11-17章沪淦卜仁祥李宗宣
章沪淦,卜仁祥,李宗宣
(大连海事大学航海学院,辽宁 大连 116026)
1 引言
由于欠驱动船舶路径跟踪存在速度不易测量、模型不确定以及外界干扰等问题,因此对其控制是比较困难的。近年以来,对船舶路径跟踪控制问题的研究,已有许多研究成果。
文献[1]针对存在模型不确定和外界干扰的轨迹跟踪问题,提出了一种基于动态面控制和最小学习参数法的自适应滑模算法,减少了计算量,避免了“维数灾难”问题。文献[2]针对船速与艏摇角速度均不可测的三自由度欠驱动船舶轨迹跟踪问题,考虑在海洋环境扰动未知,提出带非线性观测器的动态面自适应输出反馈控制方法。文献[3]提出一种基于工程解耦思想的非线性迭代滑模航迹跟踪控制器,实现欠驱动无人水下航行器,在未知海流干扰下的三维航迹跟踪。文献[4]设计了解析模型预测控制器(MPC),以对路径跟踪进行控制。文献[5]提出基于神经网络的电压控制量学习算法,通过在风干扰下采用LOS-PD方法经多次调参后得到大量先验数据,利用这些数据对神经网络进行训练,仿真验证了该算法对于抵抗时变风干扰的有效性。文献[6]针对模型参数不确定和外界干扰等问题,提出了一种基于上下界的滑模控制方法。文献[7]针对内部动态与外部干扰不确定、控制输入饱和以及运动状态约束等控制问题,提出了滑模自抗扰控制方法。文献[8]在Backstepping 方法基础上,引入非线性函数逼近技术对模型中不确定因素进行补偿控制。文献[9]设计增量反馈迭代滑模控制器,避免了系统中不确定项及风流干扰的影响。文献[10]提出一种基于Lyapunov 稳定性的神经元自适应迭代滑模控制算法。能有效地处理参数不确定和未知干扰问题。文献[11]针对状态不可测、外部干扰未知、以及状态与输入受限制的离散系统,将高阶观测器、干扰补偿控制与标准MPC相结合,提出一种新的MPC方法。文献[12]通过对跟踪偏差进行输入输出解耦,设计了输出反馈控制器,在仅有平面轨迹和船位已知条件下可完成欠驱动船舶轨迹跟踪。
参考以上文献研究成果,本文设计一种结合LESO的滑模控制器。首先为了减小船舶运动至转向点处的超调,对船舶路径进行预测。根据此预测值和参考路径值提前对未来路径误差进行计算,并采用Backstepping算法设计参考艏向角,以使船在转向点处提前打舵转弯。其次,利用双曲正切函数设计滑模控制器,对艏向进行控制。针对外界干扰和不确定参数问题,引入LESO对进行逼近,以提高控制器的鲁棒性。并通过非线性观测器和LESO对船舶纵向速度、横向速度及转艏角速度进行估计,避免速度不易测量问题。最终仿真结果验证了所提控制算法的有效性。
2 船舶运动模型
2.1 MMG模型
本文以MMG (mathematical model group) 模型作为船舶运动数学模型进仿真。MMG模型是基于深层次的理论分析结合大量的试验进行研究的,其将作用于船舶上的流体动力(矩)分解为作用于船体、螺旋桨和舵上的流体动力(矩),并考虑各流体动力(矩)之间的相互影响[7]。
在空间固定坐标系中,船舶重心在固定坐标系的位置用x0、y0表示,规定x0轴指向正北;船首尾中心线与x0轴的夹角即艏向角用φ表示;船舶运动速度在Oxyz坐标系上沿x轴和y轴上的分量分别为u和v,u为对地前进速度,v为对地横移速度,船首绕z轴旋转的角速度为r,对地合速度V=(u2+v2)1/2,漂角β=arctan(v/u),δ为舵角。船舶在平面内的位置与运动参数如图1。

图1 船舶平面位置与运动参数
考虑风浪流干扰的船舶MMG模型可表示为[6]
(1)
式中,m为船舶质量,mx和my为附加质量,XH、YH和NH为裸船体,XP、YP和NP为螺旋桨力(矩),φc和Vc分别为流的流向和流速,XW、YW和NW为风力(矩),XWave、YWave和NWave为浪力(矩),Izz为船舶绕竖直轴的惯性矩,Jzz为附加惯性矩,XR、YR和NR为舵力(矩),其计算如下
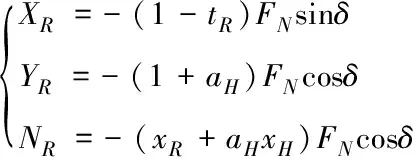
(2)
式中,tR是舵阻力减额份数,αH是操舵引起的船体附加横向力与舵横向力的比值,xH是操舵诱导船体横向力作用中心到船舶重心的距离,FN是舵正压力
2.2 设计模型
路径跟踪不需要考虑时间因素,因此本文将螺旋桨转速设为定值,只考虑舵角输入。则式(1)可以简化为如下式(3)的设计模型

(3)
式中,K是船舶旋回性指数,T是追随性指数,f1是内部模型不确定项,d是外界干扰不确定项,f是模型不确定项f1和外界干扰d的总和,即总未知项。式中的纵向速度u、横向速度v以及转艏角速度r,在实际中均不易测量。
2.3 控制目标与假设条件
由于路径跟踪不需要考虑纵向位移,只需使横向位移y镇定为0,便可使船跟踪上路径。因此,本文控制目标是,提前设定螺旋桨转速,设计合适的舵角使船跟踪上参考路径,即满足横向位移偏差ye=0。在设计控制器过程中,所需的假设条件如下:
1) 船舶状态值,x、y和φ可以被获得;
2) 不确定项f有界,即|f| 其中1)可以通过船舶上的测量设备来满足,2)是系统可控的必要条件。3)位移是加速度随时间推移的二次积分,相当于累加和,因此在前进运动时,加速度大于0,故其比位移要小,并且有界。 本文路径跟踪控制器由两部分组成,第一部分是基于预测的未来误差和backstepping算法设计参考艏向角;第二部分是利用非线性滑模控制器和LESO实现艏向控制。控制结构如图2所示。 图2 整体控制结构 本节利用backstepping算法根据预测的未来误差,设计参考艏向角φd。首先对横向位移偏差ye=y-yd求导,考虑到直线跟踪为横向位移y的镇定问题,因此不失一般性地将yd导数设为0,并将式(3)代入 (4) 根据式(4)设计参考艏向角 φd1=-c0tanh(c1ye)-β (5) (6) 因此,所设计的参考艏向式(5)可以使路径偏差趋于0。然而,在大多数研究中,只对当前时刻的路径偏差ye进行了考虑,这容易在转向点处产生超调。有鉴于此,本文通过对船舶未来路径进行预测,进而对当前和未来时刻的路径偏差都进行了考虑。这可使船提前预测前方路径,从而尽早转向,以避免超调。首先根据式(3)和欧拉迭代法,对未来时域n内的所有船舶路径进行预测 (7) (8) 通过式(8)的预测值和参考路径yd,计算未来误差ēy(k+j),j=1, 2, …,n如下 (9) 根据式(9),构建包含当前时刻和未来时刻的路径总误差如下 (10) 式中,P、Q是权重,以调节当前时刻误差与未来误差之间的平衡。根据式(10)设计虚拟参考艏向为 φd=-c1tanh(c0yE)-β (11) 本节设计非线性滑模控制器,对艏向进行控制,使艏向角φ跟踪上参考艏向φd。首先利用双曲正切函数设计滑模面 (12) 式中,c2和c3是正的设计参数,对式(12)求导有 (13) 将式(1)和(3)代入(13)则可得: (14) (15) (16) 因此,采用式(15)控制律可以使艏向跟踪上参考艏向角。 本节利用LESO对艏向控制中的总未知项f和转艏角速度r进行估计。韩京清先生基于PID提出一种以ESO为核心的ADRC控制算法[13],之后高志强博士进一步设计了以LESO为核心的线性ADRC技术[14]。本文参考LESO算法并根据式(3)中的第三、四项,设计艏向二阶系统的LESO如下 (17) (18) (19) 式中,γ是正系数,对式(19)求导有 (20) (21) 为验证所设计控制器的有效性,进行对比仿真。以大连海事大学实习船育龙轮为仿真对象,以式(1)中MMG模型为仿真模型。育龙轮参数见表1 表1 船舶参数 式(1)中的风力(矩)XW、YW和NW计算如下[7] (22) 式中,ρα是空气密度,αR是相对风向角,UR是相对风速,Af和As分别是船舶水线以上的正投影面积和侧投影面积,Loα是船舶总长,Cwx(αR)、Cwy(αR)和Cwn(αR) 分别是风压力(矩)系数。 由于大型船舶在航行中本身就可以抵抗一阶浪干扰,所以本文只考虑二阶浪干扰,其浪力(矩)XWave、YWave和NWave计算如下[15] (23) 式中,λ是浪波长,χ是波浪遭遇角,ρ是海水密度,α是浪波幅,L是船长,CXw(λ)、CYw(λ)和CNw(λ)分别是波浪漂移力(矩)系数。 船舶初始状态:u=7.2m/s,v=0,r=0,φ=0, (x0,y0)=(0, 200m)。外界干扰,风速: 10m/s,风向:30sin(0.02t)+45;流速: 1.0 m/s,流向:10sin(0.005t)+45;浪波长:83m,波浪遭遇角:φ+135°-30°sin(0.02t)。控制器参数为co=0.003,c1=π/3,c2=0.1,c3=0.4,c4=0.1。参考路径由相邻的参考定点连接而成,定点位置:(0,0), (4000,0), (7000,1500), (10000,4000), (15000,4000)。 图3 路径跟踪 图4 艏向角和舵角 图5 纵向速度u和横向速度v 图6 总未知项f和转艏角速度r 图3展示了路径跟踪结果,y1是预测了船舶未来路径偏差而设计参考艏向的路径图,此处选择预测范围n=45,y2代表未经过预测的路径,即n=0。可以看到两个控制器都可以使船准确地跟踪上参考路径,但由于y1提前对未来路径和偏差进行了考虑,所以其跟踪速度较快,并且在转向点处可以提前打舵转向,减小了超调。图4展示了船舶运动过程中的艏向和舵角变化,由于时变风浪流干扰的影响,使其都有小幅度的振荡,以抵抗干扰的外作用。图5描述了所设计的非线性观测器对纵向速度u和横向速度v的估计能力,可以看出其可以精确地估计出u和v。图6说明了所引入的LESO对转艏角速度r和总未知项f的逼近能力,其结果表明了LESO可以有效地逼近r和f。 本文为解决欠驱动船舶路径跟踪中的速度不易测量、模型不确定与外界干扰等问题,提出一种结合LESO的滑模控制方法。首先,为了使船在转向点处提前打舵进行转弯,对船舶路径进行了预测,据此预测值和参考路径值提前对路径未来误差进行计算,并采用Backstepping算法设计参考艏向角。其次,采用双曲正切函数设计滑模控制器,对艏向进行控制。针对外界干扰和不确定参数问题,引入了LESO对其进行逼近,以提高控制器的鲁棒性。并利用非线性观测器和LESO对u、v以及r进行估计,避免速度不易测量问题。最终仿真结果表明,在各个速度不可测的情况下,所提控制器仍能使船在风浪流时变干扰下准确地跟踪上参考路径,并且在转向点处可以提前打舵进行转向,以避免超调。这些结果验证了所提控制算法的有效性。
3 路径跟踪控制器

3.1 Backstepping算法

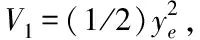



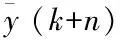



3.2 非线性滑模控制器的设计

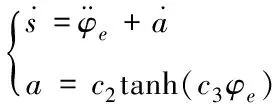
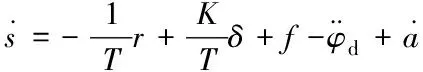
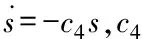
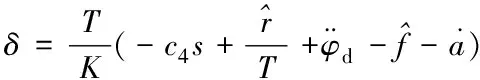

3.3 LESO设计

3.4 非线性观测器







4 船舶路径跟踪控制的仿真研究
4.1 仿真模型与参数

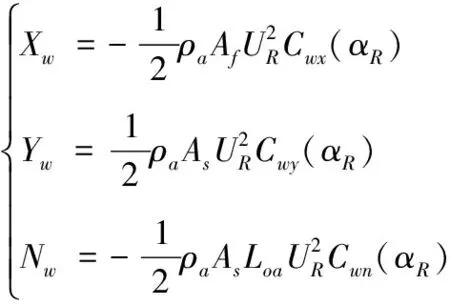

4.2 仿真结果




5 结语
