加权K-prototype-粗糙集的航班延误等级划分研究

王兴隆，纪君柔，石宗北

(中国民航大学空中交通管理学院，天津 300300)

1 引言

随着航班流的增多，空域资源的紧缺，航班延误也日益增多，而对航班延误程度进行有效评估，制定切实可行的航班延误等级划分规则是减少延误成本，进行协同流量管理并且建立相应的应急预案的关键依据，具有很大的实际应用价值。

2012年，Raj Bandyopadhyay[1]等使用线性回归来确定影响航班延误的因素，并采用分类器(SVM)来分析航班延误，2017年，Suvojit Manna[2]等采用航班延误的六个延误属性，建立梯度增强决策树模型用来分析航班延误。2014年，顾绍康[3]根据时空和空间两个角度的评估指标建立了航班延误程度实时评估指标体系，2015年，孟会芳[4]以国内某大型枢纽机场为应用背景，构建了基于投票聚类的一段时间内的航班延误等级划分策略，2018年，吴仁彪[5]等人提出了基于双通道卷积神经网络(DCNN)的航班延误预测模型，将延误时间进行等级划分，将预测问题转化为分类问题。

以上研究只是提出数值属性指标对航班延误程度进行了评估，同时并未确定具体的判断准则，本文同时提出数值属性指标和类别属性指标，利用加权k-prototypes聚类算法对航班延误程度进行了等级评估，并进一步结合粗糙集理论知识，利用Rosetta软件建立了科学有效的延误航班等级划分规则，确定了直观并具有高准确率的延误等级判断准则。

2 加权K-prototypes-粗糙集航班延误等级划分模型

2.1 航班延误等级划分指标选择

图1为延误航班等级划分流程图。

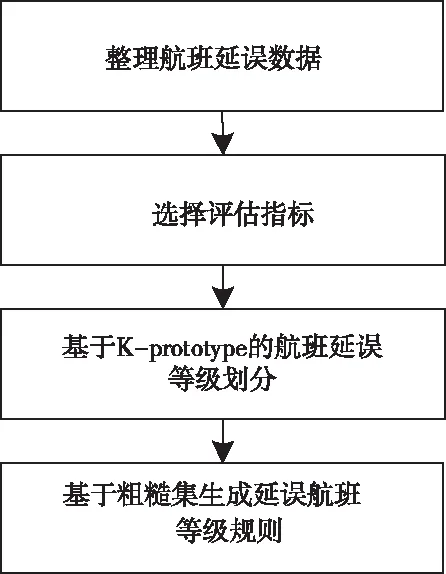
图1 延误航班等级划分流程图

由图1可知对航班延误程度的等级进行划分，需考虑多个能反映航班延误程度的指标，每个指标均能从某一方面反映延误状况，结合我国航空运输的特点和实际情况，本文提出了6个衡量延误程度的指标：

1)延误时间指标

当延误时间越长，航班延误成本越高，并对后续航班造成的影响更大，波及延误更广，对机场，航空公司以及旅客产生直接的延误经济损失，为此选取延误时间为衡量延误程度的权重最大的指标。

2)飞行时间指标

飞行时间越长，油耗成本越高，若延误航班的飞行时间越长，那么在飞行中产生影响航班安全飞行和实际飞行时长的因素几率就越大，且可能会导致航班需要过夜，增加了航空公司的延误成本。飞行时间从航空公司角度反映了延误程度。

3)延误人数指标

延误人数越多，产生的旅客经济损失就越大，这种经济损失可描述为延误时间占用了旅客正常的工作时间，延误人数是从旅客角度评价延误程度。

4)飞行距离指标

延误航班飞行距离越长，那么航班经过的管制扇区就相对越多，需要进行管制移交的次数就越多，受影响的管制员就越多，飞行距离是从管制员角度考虑延误程度。

5)经停指标

延误航班是否需要经停反映了受影响的机场个数，经停延误航班不仅对目的地机场产生影响同时也会影响经停机场，航班是否经停是从机场角度确定延误程度。

6)机型指标

延误航班机型越大，所需尾流间隔也越大，恢复航班运行难度也相对较大，地面等待以及空中等待经济损失也越大，机型指标是从等待经济损失角度确定延误程度。

6个航班延误评价指标具体表示如表1所示：

表1 航班延误等级评价指标

2.2 基于加权K-prototype的航班延误等级划分

聚类分析是一种无监督的学习，对应用于大规模数据集的划分具有很大的优势，一般的聚类方法如：K-means算法[6]，K-modes算法[7]，RW-CLOPE算法[8]等只能对单一属性指标数据进行处理，而本文在对延误航班进行等级划分时采用的六个评价指标包含了数值属性指标和类别属性指标，k-prototype算法[9]是能够对混合属性数据进行聚类的一种有效算法。

1)最佳聚类数K的确定

在聚类分析时，最佳聚类数的选择具有随机性导致聚类结果稳定性较差，因此本文通过手肘法和轮廓系数法相结合对评价指标进行计算分析确定最佳聚类数，从而保证聚类结果稳定可靠。

手肘法是一种基于误差平方和(SSE)的K值选择算法，随着聚类数K的增大，每个类的聚合程度会逐渐提高，误差平方和SSE自然会逐渐变小。当K小于真实聚类数时，由于K的增大会大幅增加每个类的聚合程度，故SSE的下降幅度会很大，而当K到达真实聚类数时，SSE的下降幅度会骤减，然后随着K值的继续增大而趋于平缓， SSE的计算公式如下

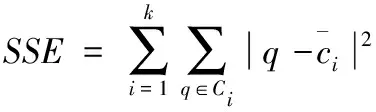
(1)

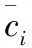
轮廓系数法的核心指标是轮廓系数(Silhouette Coefficient)，某个延误航班Xi轮廓系数定义如下

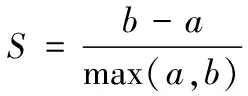
(2)

式中：a是Xi与同类中其它延误航班的平均距离，b是Xi与最近类中所有延误航班的平均距离。最近簇的定义为

(3)

式中：qk是某个类Ck中的一个延误航班。

求出所有延误航班的轮廓系数后再求平均值就得到了平均轮廓系数，平均轮廓系数越大，聚类效果越好。

2) k-prototypes算法的加权改进

在实际航班运行中，不同评价指标在对延误航班的等级划分中所占比重也不相同，因此本文对k-prototypes算法进行了加权改进。

设X=[X1，X2，X3，…Xn]为n个延误航班集合，其中Xi=[xi1，xi2，…xip，…xim]表示具有m个延误评价指标的第i个延误航班，1至p下标为数值属性指标，p+1至m下标为类别属性指标，Y=[Y1，Y2，Y3，…Yk]为K个类的中心原型延误航班的集合，其中Yj=[yk1，yk2，…ykp，…ykm]表示第j个类中具有m个评价指标值的中心原型航班。

数值属性指标之间采用欧几里得距离计算，计算公式为

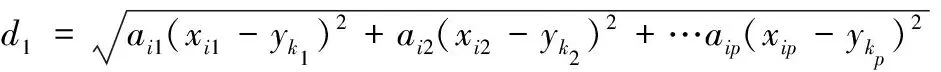
(4)

式中：ai1，ai2，…aip为不同数值评价指标的权重值。

类别属性指标之间的采用海明威距离计算，计算公式为

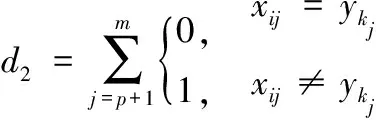
(5)

相异度距离为

d=d2+γd2

(6)

式中，γ为分类属性权重值。

采用加权K-prototype聚类算法仅能对每个延误航班的延误等级进行划分，而不能建立有效航班延误等级划分规则。

2.3 基于粗糙集的航班延误等级规则建立方法

本文采取粗糙集理论[10-11]对航班延误等级进行规则建立，粗糙集理论可以在信息不完整和信息不一致下，用来规约数据集合，发掘隐藏数据相关性，以产生有用的分类规则。

航班延误等级判别的知识表达系统为S=(U，A，V，f)，其中U为航班延误特征论域；A为航班延误属性集合，由条件属性C和决策属性D组成，C={延误时间，延误人数，延误航班机型，飞行距离，是否经停，飞行时间}，D={延误等级}；V为属性对应的值域，f：U×A→V是一个航班延误等级信息函数，为每个航班延误等级对象属性赋予一个信息值。航班延误等级规则生成步骤如下：

1)航班延误属性数值进行离散化处理

2)利用Johnson算法进行属性约简，属性约简的目的是将多余的属性值删除

3)等价类和上下近似集的获取

4)生成航班延误等级的划分规则

2.4 模型计算步骤

模型计算步骤如下：

Step 1：输入样本数据，结合“手肘法”和轮廓系数法确定样本数据最佳聚类数K，每个类选取一个中心原型。

Step 2：根据式(6)将样本分配到距离中心原型最近的那个类，每次分配后，更新类的中心原型。

Step 3：在所有的样本都分到各自的类中后，重新计算样本到中心原型的距离。如果一个样本距离新的中心原型比距原来的中心原型要近，那就重新分配到新的中心原型的类中。

Step 4：重复Step 3，直到没有样本对应的类再改变，聚类结束，得到每个航班对应的延误等级。

Step 5：选取航班延误特征和对应的延误等级，基于粗糙集理论构建航班延误等级识别知识表达体系。

Step 6：采用基于布尔逻辑离散化算法对延误属性数据的离散化。

Step 7：采用Johnson贪婪算法，对离散化的航班延误属性进行约简，删除冗余属性，提取航班延误等级划分规则。

Step 8：计算航班延误等级规则划分精度。

3 实例验证

3.1 数据准备

选取某大型枢纽机场一月份的航班延误数据，共选取了4557条延误航班数据作为样本，因为数据值差异性过大，为了增加结果的准确性，将数值指标根据式(7)进行归一化处理，将各数值指标取值控制在[0，1]之间。

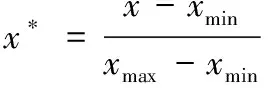
(7)

其中x为样本数据，xmin为所有样本数据的最小值，xmax为所有样本数据的最大值。经过归一化后部分样本数据如表2所示。

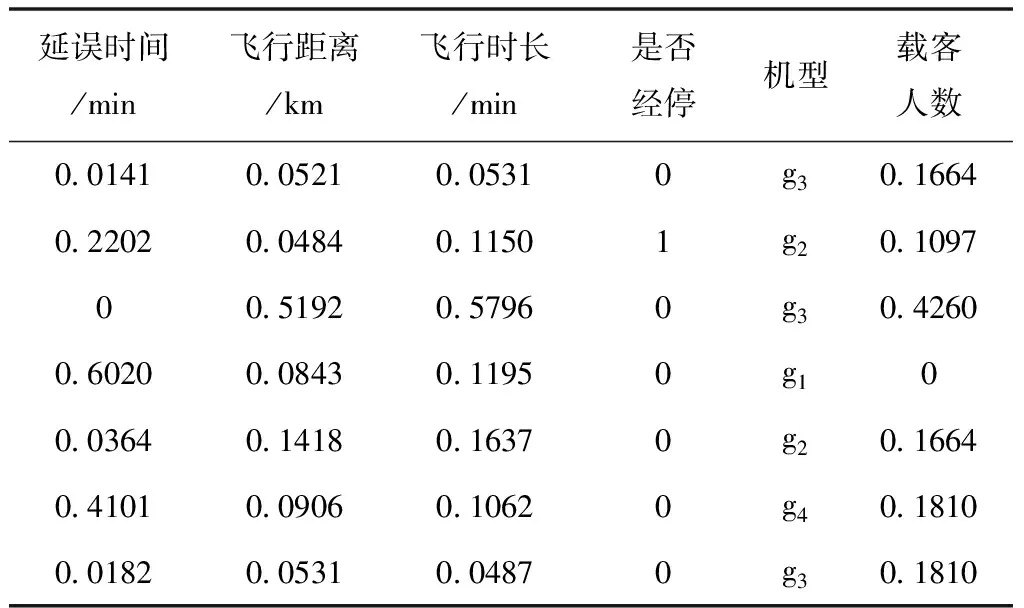
表2 归一化后的航班延误数据

3.2 最佳聚类数K的确定

由图2可以看出该类方法得到的最佳聚类的K的取值可能为3，4，5。

“手肘法”Python实现结果如图3所示。

由图3可以看出该类方法K=2时平均轮廓系数最大。

轮廓系数法Python实现结果如图4所示。

手肘法具体应用于具体的数据集时，会出现如图2一样不明显的“肘点”，导致K值取值具有较大误差，因此本文同时结合轮廓系数法从而准确的确定最佳聚类数，由图3可得，在K=2的时候平均轮廓系数最大，因为在K=2时由图2可看出SSE过大，所以该聚类数不太理想，在K=4的时候，平均轮廓系数也较大，且也符合手肘法得到的K值范围，综上所述，本文的最佳聚类数选取为4类。

图2 “手肘法”折线图

图3 轮廓系数法折线图

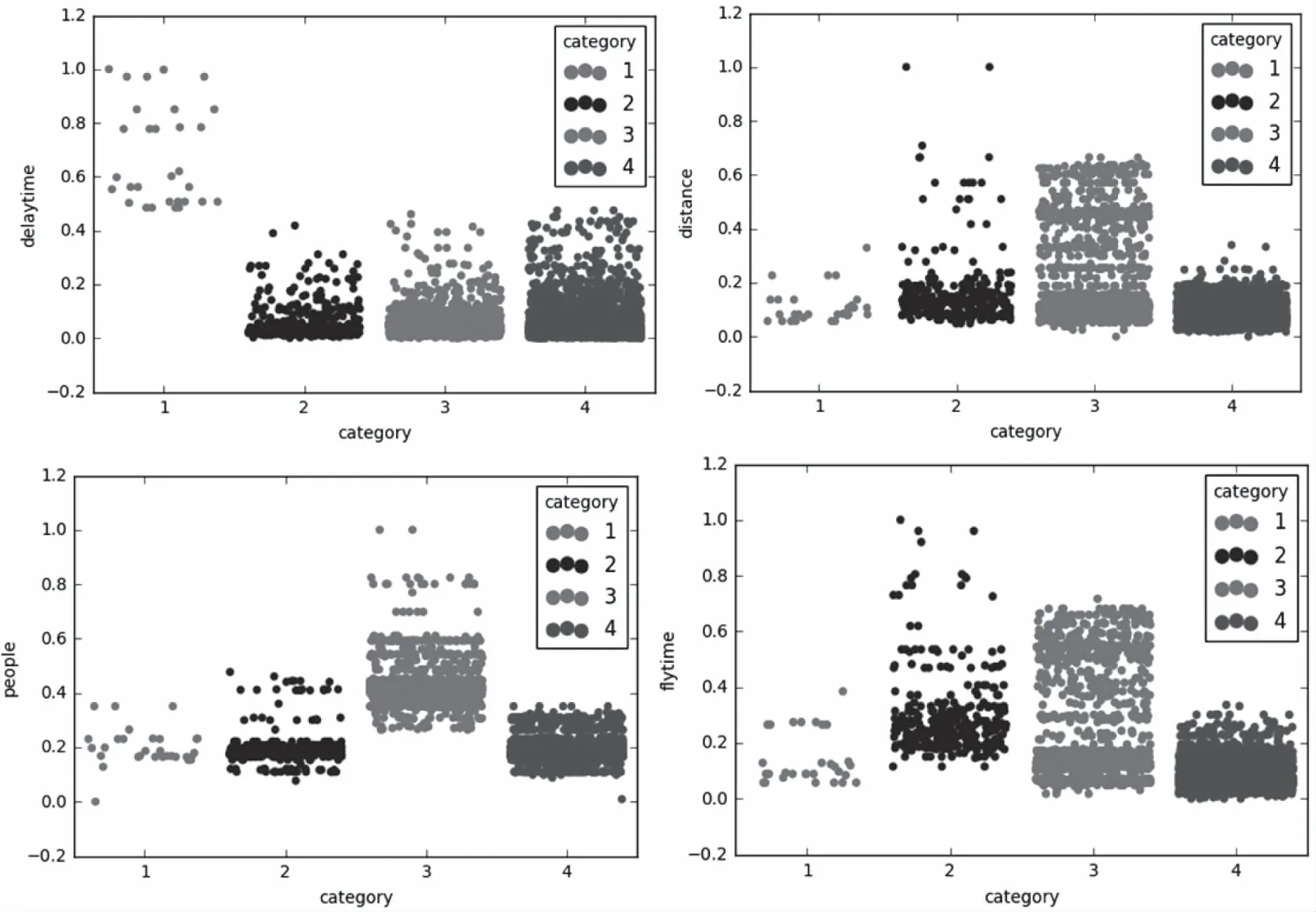
图4 数值属性指标分布图

4 实验结果分析

本文结合实际航班运行成本将平均延误时间的权重设置为0.8，飞行距离和飞行时间的权重设置为0.1，载客人数的权重设置为0.4，γ设置为0.2。

当K=4时采用改进的加权K-Prototypes聚类算法得到聚类结果，第一类航班有35架次占比1%，第二类延误航班有323架次占比7%，第三类延误航班有1415架次占比31%，第四类延误航班有2784架次占比61%。

整理每个类别里延误航班的每个评价指标分布，并进行对比分析，确定每种类别对应的航班延误级别。延误等级共有4级，各类延误指标分布图如图4和图5所示。

由图4图5可知，第一类延误航班的延误时间远远高于其它三类，定义为重度延误；第三类延误航班载客人数以及大机型以及超大机型的占比也显著多于其它两类，但延误时间相差不大，定义为中度延误；第二类延误航班的六个评价指标均高于第四类延误航班，定义为一般延误，则第四类延误航班定义为轻度延误。

采用Rosetta 粗糙集软件利用K-prototype聚类分析的结果作为分析样本进行计算分析。航班延误属性为延误时间、飞行距离、飞行时间、载客人数、是否经停以及机型，设定决策属性为轻度延误、一般延误、中度延误、重度延误。采用Rosetta粗糙集软件中自带的 Boolean reasoning(布尔逻辑)算法和 Jonson 贪婪算法进行属性的离散化和约简，发现是否经停为冗余属性，并设置精确度和覆盖度，得到48条划分规则，对这些划分规则结合实际进行整理分析对比得到表3航班延误等级划分。

图5 类别属性指标分布图

采用等级判别率GD来衡量该等级划分规则的精度。指标的计算公式为

(8)

其中，GID为利用等级规则对样本延误航班划分的等级与原先延误航班样本等级的差异航班数，N为判断延误等级的总样本航班数。

对样本延误航班进行抽样验证，得到该等级划分规则的等级判别率为81.9%，可见该划分规则精度较高，总体判别结果稳定，能较为准确的划分航班延误等级。

表3 航班延误等级划分规则表

5 结论

1)本文同时考虑数值属性和类别属性评估指标，采用了加权k-prototypes 算法对大量延误航班聚类分析，为延误航班划分了四个延误等级。

2)利用粗糙集理论结合实际情况，制定了航班延误等级划分规则，该规则的等级判别率达到81.9%，提供了直观有效的航班延误等级判断手段。

3)下一步的研究重点就是获取更多的航班延误数据，构建更多的反映航班延误程度的评价指标，建立更为准确的航班延误等级划分规则，提高等级判别率，并在对复杂终端区协同调度策略进行研究时考虑航班延误等级，提高等级划分模型的实际应用价值。