基于MARKOV随机信道分配的车队控制研究

乔 栋，谢亚龙，贾 权，姚 涛

(1.山西大同大学建筑与测绘工程学院，山西大同 037009;2.山西大同大学煤炭工程学院，山西大同 037009;3.山西大同大学机电工程学院，山西大同 037009;4.河北工业大学机械工程学院，天津 300401)

1 引言

随着汽车保有量急剧增加和智能交通的发展，交通拥堵不仅仅是一、二线城市具有的城市病，三、四线城市也出现了不同程度的交通拥堵现象，尤其是在中国，交通拥堵以及由汽车尾气所造成的环境污染已然成为急需解决的城市病。仅仅通过增加道路通行能力和从车辆性能方面入手，并不能很好的解决上述问题，且治标不治本。采用先进的高科技手段，即智能交通系统(Intelligent Transportation System)，成为上述问题的新思路[1-2]。

自主车队控制系统[3]作为智能交通系统未来的发展方向，是指公路系统中的车辆按照期望的队形组成车队行驶。通过车载雷达传感器[4]、超声波[5]、摄像头[6]等装置提升舒适度与安全性，但容易受到外界因素的影响，例如雾霾、大雨等。近些年，网络通信技术飞速发展[7-11]，将无线通信技术应用到自主车队控制系统中，能够有效的解决上述问题。V2V[12]V2I[13]成为必然趋势。无线通讯网络的介入，必然会带来网络的固有缺陷，例如延时、丢包、乱序和介质访问约束等。而且车辆的快速移动性，使得网络化车队控制系统有别于传统的网络控制系统，给研究人员带来了巨大的挑战，但是其应用前景广阔。

在国内，主要是Guo的团队对网络化自主车队进行研究[14-15]。而且对于网络车队控制系统的研究主要集中在通信时延方面。文献[16]通过状态估计和线性矩阵不等式方法获得了车辆间数据的最大丢包数。而文献[17]则是从一致性的角度出发，研究了车辆间的通信时延问题。目前大多数的研究都是基于单一网络因素对车队控制性能的影响，而文献[18]则是综合考虑了通信时延、丢包、乱序和数据包异步问题，构建了离散度车队数学模型，通过智能处理器保证车队稳定。车辆数量的急剧增加，使得网络化车队控制系统中的信道受限问题不可避免。文献[19]通过动态调度与静态调度结合的方法，给出了车辆间通信调度序列与控制器协同式设计方法。上述研究所获得的调度序列是基于时间调度的，而网络信道的分配是由事件驱动的(包括确定事件与随机事件)，确定事件类似与时间驱动。

本文主要研究了随机事件，即车辆间通信信道的分配是随机的，对于信道随机分配的网络化车队控制系统，基于调度的方法已不再使用。而且目前对于车队信道受限的研究主要集中在调度方向。

基于上述讨论，本文主要通过将车辆间通信信道的随机分配特性描述为转移概率部分未知的Markov模型，然后将异构网络化车队模型建模为多个状态的Markov跳跃系统，并给出了车队控制系统随机稳定的条件以及相应控制器的设计方法，最后通过仿真与实验验证了其有效性和实用性。

2 网络化自主车队建模

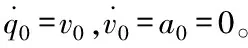
图1 异构网络化车队模型

2.1 网络化车队建模

跟随车辆i(i=1，2，…，N)的纵向动态模型表述为[15]：

其中，qi、vi和ai分别表示第i辆车的位置速度和加速度。ci是发动机的输入

其中，dmi、cdi、Ai、mi和σ分别表示第i车的拽力系数、机械阻力、横截面面积、质量和空气质量密度，σAicdi/2mi代表空气阻力，ηi是发动机的时间常数。通过反馈线性化方法，对上述非线性车辆模型进行控制器设计，则

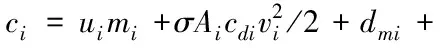
其中，ui是车辆i控制输入量。因此，车辆的近似动力传动系统表示：

(1)

为每一辆跟随车辆i设计合适的控制律ui，实现以下跟踪性能，

qi→q0+Li+di，0；vi→v0；ai→ 0

(2)

β[vi(t)-v0]-γ[ai(t)-a0]-

(3)

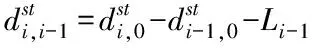
分别定义车辆i与领头车的位置、速度和加速误差信号

(4)

因此，可用下式表述第i辆车的分布式控制策略

ui(t)=-β[vi(t)-v0]-γ[ai(t)-a0]-

(5)

通过数学变换，可得第i辆车的分布式控制策略

(6)

因此，可获得第i辆车的误差模型

(7)

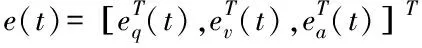
u(t)=(-k1-k2+k2C)e(t)

其中

k1=diag{k1，0，k2，0，…，kN，0，β，…，β，γ，…，γ}∈R3N×3N，

k2=diag{k1，0，k2，1，…，kN，N-1，0，…，0}∈R3N×3N

因此，基于无线网络通信的异构网络化车队控制系统为

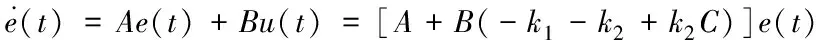
(8)

其中

η=diag{η1，η2，…，ηN}

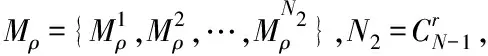
(9)

本文研究的是用于描述通讯信道的Markov过程的转移速率部分未知情形，即转移速率矩阵π=[πij]的元素部分未知。比如Markov有四个工作状态，则其对应的转移速率矩阵为

在t时刻，基于信道受限的控制策略为

u(t)=(-k1-Mρ(t)k2+Mρ(t)k2C)e(t)

(10)

因此，基于通信受限的网络化车队控制系统模型为

(11)

2.2 控制目标

为了获得期望的车间距，需要为跟随车辆设计控制器(3)，使得整个异构网络化车队控制系统满足如下性能：

1)车队稳定性：异构网络化车队控制系统随机稳定；

3 车队稳定性分析

3.1 车辆随机稳定性分析

在上一小节，得到了基于通讯信道受限的异构网络化车队模型(11)。在本小节通过以下定理能够保证跟随车辆随机稳定，而且也给出了对应控制器的设计方法。

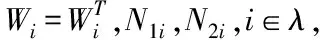
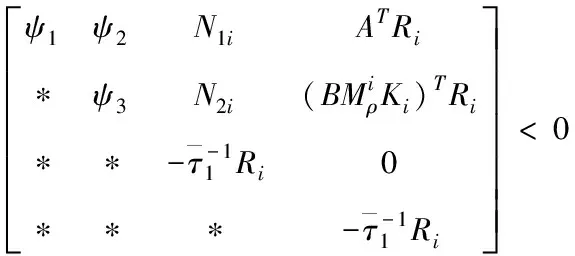
(12)

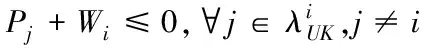
(13)

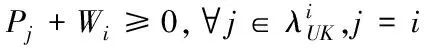
(14)

那么车队控制系统(11)随机稳定。其中

证明：定义Lyapunov-Krasovskii泛函

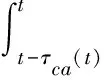
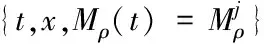
进而可知

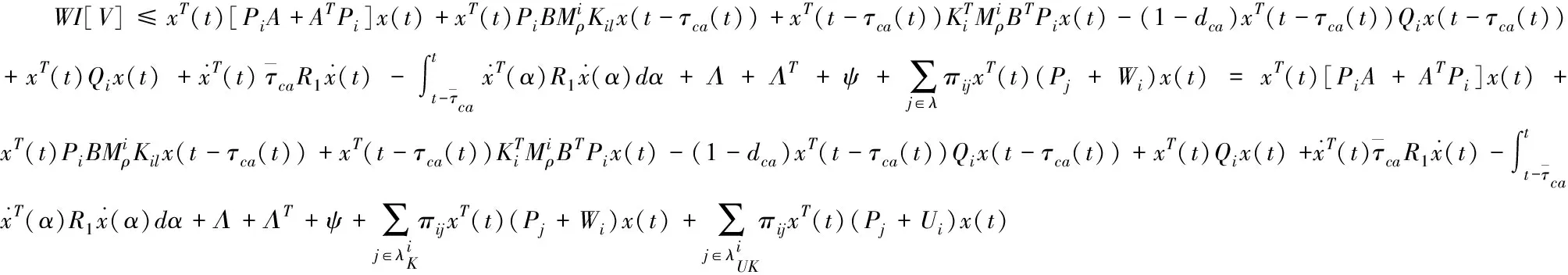
(15)

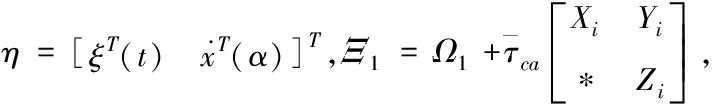
当i，j∈λ，j≠i时，πii<0且πij>0成立。结合(15)可知：如果

Ξ1+Ξ2<0

(16)

Θ≥0

(17)

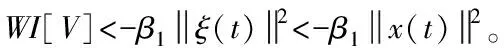
Pi>0由Schur补引理[18]可知，(17)等价于

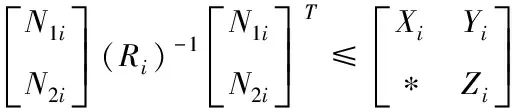
(18)

结合(16)，(18)和Schur补引理，可得(12)，证毕。

定理1给出了车辆随机稳定的理论依据。可通过如下定理求得对应控制器增益。

(19)

(20)

(21)

(22)

(23)

其中

相应的控制器增益为

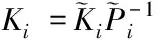
(24)

分别用矩阵J左乘和右乘(12)，并对其进行合同变换可得

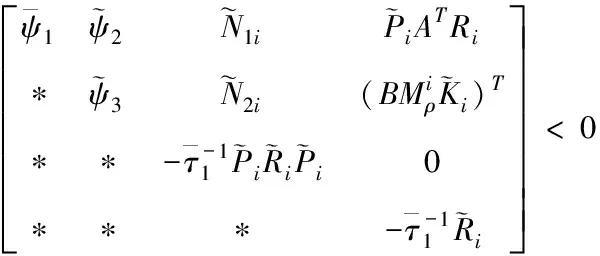
(25)

其中

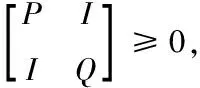
基于下列条件

最后根据文献[20]中的算法1，即可求解该问题。

3.2 车队队列稳定性分析

上一小节，给出了保证车辆随机稳定的条件以及对应控制器的设计方法，对于车队控制，为了防止追尾事故的发生，还需要满足车队队列稳定性，即车间距误差沿着队列向后逐渐递减，最终趋近于0。

通过车辆的动态模型和控制律可得，车辆i的误差方程

将式(1)和(3)带入上式可得

ki，i-1ei，0+ki，i-1ei-1，0

(26)

对式(26)Laplace变换

(27)

对(27)进行频域分析，可以通过以下定理保证车队队列稳定。

定理3：对于任意的w>0，|ei，0(jw)/ei-1，0(jw)|≤1成立，当且仅当以下条件

γ2-2βηi≥0

(28)

ki，0γ-ki，i-1γ≥0

(29)

成立，则达到车队队列稳定。

证明：为了保证车队队列稳定性，首先给出|ei，0(jw)/ei-1，0(jw)|为

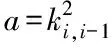
因为a>0，因此要使|ei，0(jw)/ei-1，0(jw)|≤1成立，只需b≥0 ，则车队队列稳定。如果(28)和(29)成立，则b≥0 成立，证毕。

本文所提出的控制律能够保证车队实现零稳态误差。在t时刻，定义领头车的速度与稳态速度v0的偏差为ε0(t)=v0(t)-v0，因此

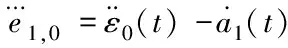
(30)

通过式(30)和(1)可得

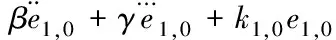
(31)

对式(31)Laplace变换，可得第一辆跟随车辆与领头车的车间距误差变换关系

(32)

不失一般性，假设领头车在有限时间tf内达到最终的稳态值，则当t≥tf时，ε0(t)-ε0(tf)=0成立。所以

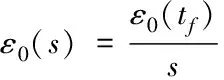
(33)

最后，通过使用终值定理和式(31)、(32)和(33)，可得

=0

其中，i=1，2，…，N。因此可以保证车队的零稳态误差。

3.3 车队控制算法

下面给出整个异构网络化车队控制系统的算法过程。

算法1：

1)通过反馈线性化方法设计控制器(3)，该方式在传统的非线性控制以及其它文献中频繁使用，本文给出，体现本文所设计控制算法的完整性。

2)根据定理2，利用LMI工具箱获得整个车队控制增益k1，k2；

3)检验所得的控制器增益k1和k2是否满足队列稳定性的条件(23)和(24)。如果满足，则说明所获得的控制器增益满足车队队列稳定性要求。反之，需要重新设定相关矩阵，返回到第二步重新求解。

4 MATLAB仿真与实验

本小节首先通过MATLAB仿真验证了所提出算法的有效性，最后通过由Arduino小车所组成的车队验证了本文的实用性。

4.1 MATLAB仿真

通过MATLAB软件搭建了由5辆车组成的网络化车队控制系统，并将本文所提出的算法应用到上述搭建的模型中。

假设领头车初始速度为30m/s，且加速度满足如下特性

假设对应Markov的转移速率矩阵为

其中‘？’代表未知的元素。信道随机分配的状态序列如图2所示。

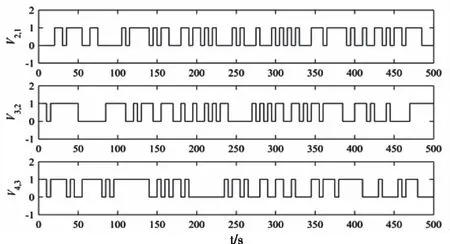
图2 跟随车辆与其直接前车的通信序列

通过定理3.2求得控制器增益为

k1=diag{ 1.2569， 1.1574， 1.0856， 1.0485，2.5815， 2.5815， 2.5815， 2.5815，2.1694， 2.1694， 2.1694， 2.1694}

k2=diag{ 3.6236， 1.69262， 2.6598， 2.1653，0， 0， 0， 0， 0， 0， 0， 0}

从图3-5可以看出，对于信道受限的异构网络化自主车队控制系统，本文研究的算法能够保证车队随机稳定，且整个车队队列稳定。

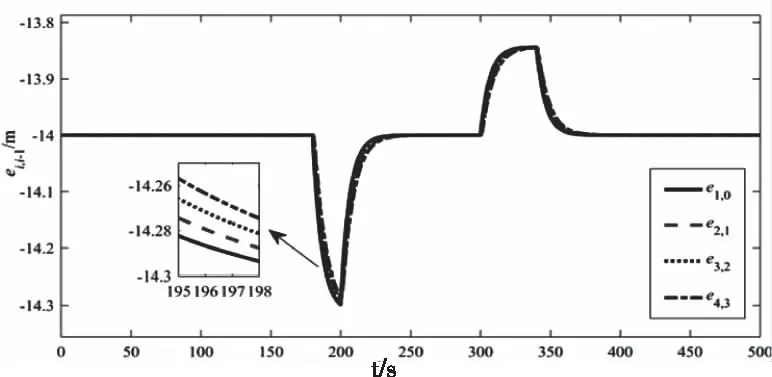
图3 相邻车辆的车间距误差

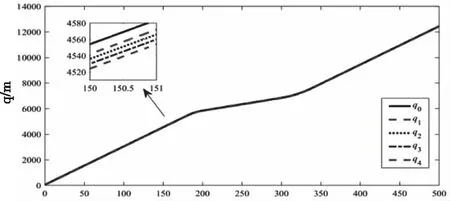
图4 车辆的位置响应特性

图5 车辆的速度响应特性

4.2 Arduino车队实验

为了验证本文算法的实用性，本小节通过4辆Arduino智能小车来模拟信道受限的异构自主车队控制系统，如图6和图7。车辆间采用的无线模块为APC220，工作频率为418MHz到455MHz，传输距离为1000m。

图6 Arduino小车

图7 智能车队

文所提出的算法，能够使得跟随车辆维持期望的车间距。

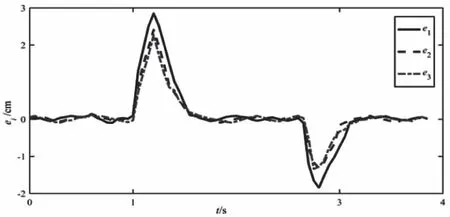
图8 智能车队车间距误差响应特性

5 结论

本文研究了通讯信道受限的异构网络化车队控制系统，将通信信道建模为转移概率部分未知的多状态Markov跳跃模型，通过Lyapunov定理和LMI工具，获得了车辆随机稳定性条件以及对应控制器的设计方法，通过频域分析给出了车队队列稳定性条件。最后通过MATLAB仿真和Arduino车队实验，验证了本文所提出算法的有效性和实用性。

本文研究的是跟随车辆与其直接前车通讯信道受限问题，与领头车辆的通讯是不受限的。而跟随车辆不仅与其直接前车的通讯受限，而且与领头车辆的通讯也受限情形，作为将来的研究方向。