基于2D与3D匹配模型的变压器全损耗特征计算

王 荆，潘莉丽，韩彦华，江天炎

(1.国网陕西省电力公司电力科学研究院，陕西 西安 710100;2.国网陕西电力公司西安供电公司，陕西 西安 710032;3.重庆理工大学，重庆 400054)

1 引言

电力变压器绕组形变评估是影响其健康状态和绝缘寿命的难点问题，准确计算变压器全损耗，对变压器绕组形变程度的准确评估具有的重要意义[1-3]。大容量电力变压器正常运行时，其杂散损耗可以达到负载损耗的30%～40%，变压器的内部损耗计算与分布规律分析对变压器的经济运行、降损和节能具有重要的意义[4，5]。然而随着变压器等级容量的不断提升，其内部结构电磁关系也更为复杂，使用传统的方法进行损耗分析往往具有较大的偏差。

在大型电力变压器中，绕组线圈中流过较大的电流，不同的绕组结构产生的损耗值与分布也有所不同，同时在导体和铁芯中产生铜损耗和磁滞损耗和杂散损耗，随着电流数值的增大，杂散损耗会成倍增加，变压器损耗分布和绕组热点分布与变压器散热有着密切联系，损耗计算是变压器结构和绝缘配合设计的关键问题。文献[6]中总结出了变压器空载和满载工况下的变压器计算方法，并首先给出了相应的计算公式。文献[7]中提出了一种改进的谐波损耗公式计算方法。文献[8]中基于有限元法建立了变压器二维有限元模型，得到了绕组的涡流损耗计算模型。文献[9]分析了单相三柱变压器的铁芯损耗，构建了基于MAGNET软件的变压器损耗瞬态计算方法。文献[10]建立了简化的变压器三维有限元模型，分析了变压器的漏磁分布并计算了金属结构件的损耗。这些方法可以分为两类，一类是通过试验或经验总结的公式计算方法，该法计算方法简洁、效率高且易操作，但是对于大型的电力变压器而言，其具有更加复杂的结构，用此方法进行损耗的估算具有较大的偏差。另一种是基于计算机技术，利用有限元数值计算的方法来分析变压器的损耗，随着计算机技术的发展，该法能够在保证复杂结构变压器损耗计算效率的同时，还能够具有较好的精度，受到国内外学者的青睐[11，12]。

然而，现有变压器的损耗计算模型难以实现变压器全损耗的计算，没有考虑到不同类型的损耗一体化表现，其主要原因在于3D的损耗计算模型涉及到空间尺度的问题，绕组损耗的计算所需要的较小离散单元对于变压器大空间的杂散损耗的计算而言，常常会导致空间离散的的失败或单元的过度扭曲，难以保证计算的收敛和准确性。因此本文提出了一种基于2D与3D模型匹配的变压器损耗混合模型计算方法，能够准确计算绕组等损耗分布特征同时保证计算的收敛与高效性。并以一台400 kVA的三相电力变压器为例，分析了建模的基本方法和理论并对变压器内部损耗的特征规律进行了分析，为工程设计制造提供参考，对提高变压器稳定性与可靠性具有重要意义。

2 基本建模与耦合控制方程

2.1 有限元混合模型

有限元法(Finite Element Method，简称 FEM)，将整个求解域化分为一定数量的有限单元，各单元之间通过节点相连，应用求解的边界原理和选取适当的形函数，分别求解每个单元，再将结果汇总起来，便可以得到整个区域的解[13]。

本文以一台容量为400 kVA的三相电力变压器为例，其基本参数见表1。

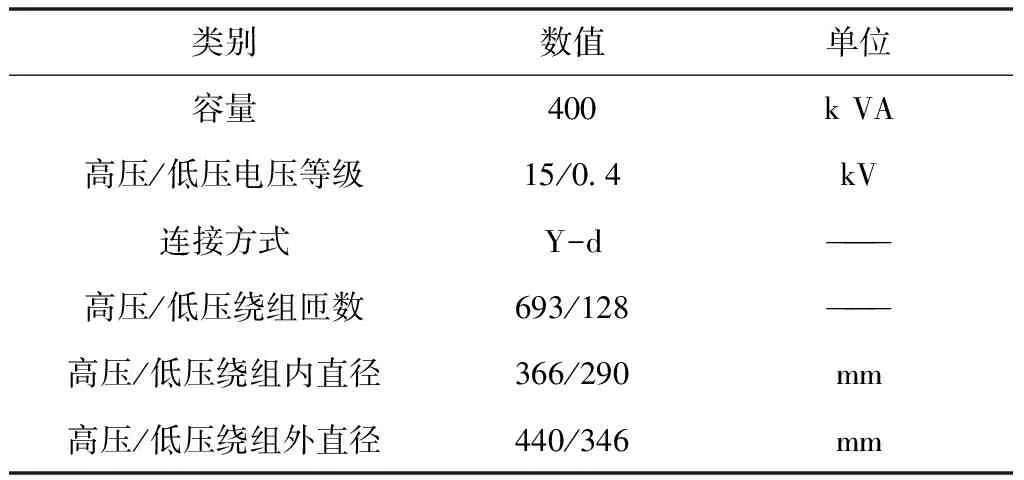
表1 变压器基本参数

变压器内部结构复杂，零部件众多，在搭建有限元模型时应依据研究目的对变压器模型进行适当简化，从而计算结果的有效性与准确性。变压器损耗计算主要包括绕组铜损耗，铁芯的磁滞损耗和周围结构所产生的杂散损耗，在搭建有限元模型时，主要针对铁芯、绕组以及绕组周边的结构件进行建模，主要包括固定零部件与变压器外壳，如图1。同时为计算绕组电流密度的分布及铜损耗，搭建了与3D模型相匹配的2D对称模型，低压绕组包含4根平行导线，尺寸为3.5×12 mm，高压绕组截面为2.3×3.7 mm，如图2。

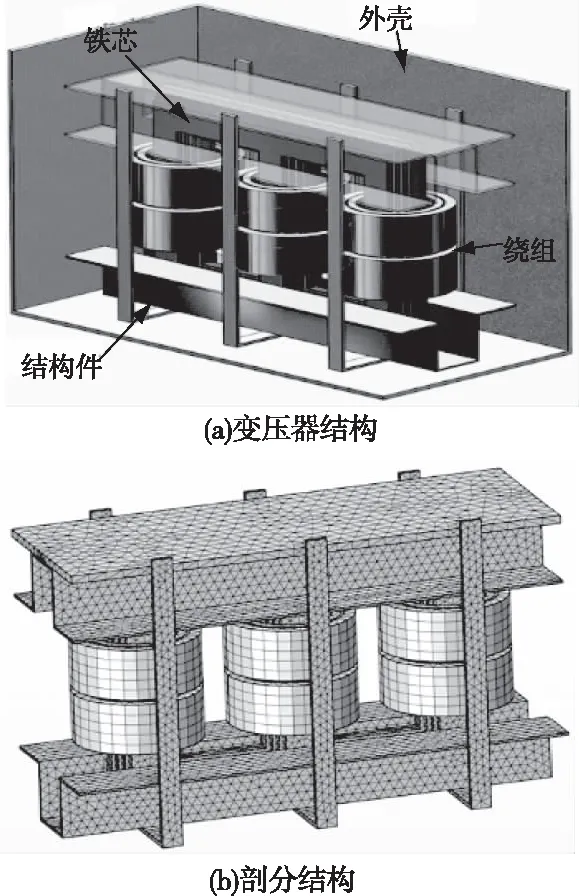
图1 变压器内部简化结构

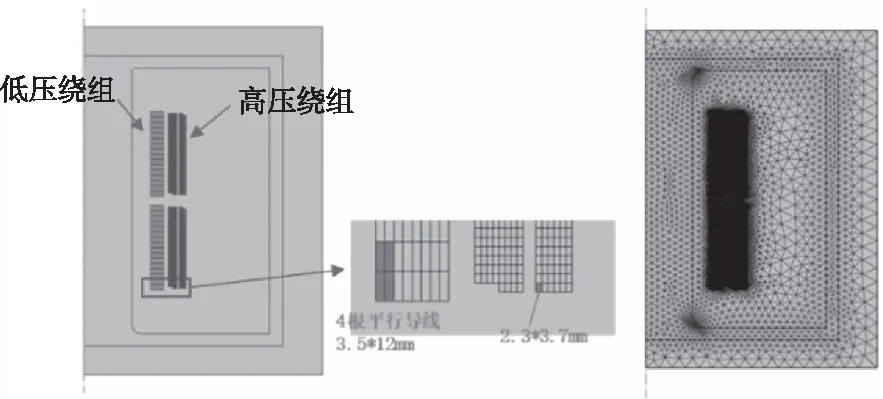
图2 绕组模型

2.2 磁场分布计算

本文建立如图1所示的电磁场计算模型，并且利用有限元法计算了变压器内电磁场的分布情况，如图3所示。电磁场计算边界控制方程如式(1)、(2)所示[14]。

(1)

式中：Aφ为磁矢势，v为磁阻率，Jφ为源电流密度，Ht为切向磁场强度。磁通密度由下式计算。

(2)

式中：Br和Bz分别为径向和轴向磁感应强度。

如图3所示为变压器在运行时铁芯和绕组的磁场密度分布情况，在铁芯的上下铁轭的磁通密度较大，最大值出现在靠近线圈的拐角处。而在绕组中磁通密度的分布呈现椭圆形，最大值出现在高压绕组夹缝的中间位置，约为0.1T。

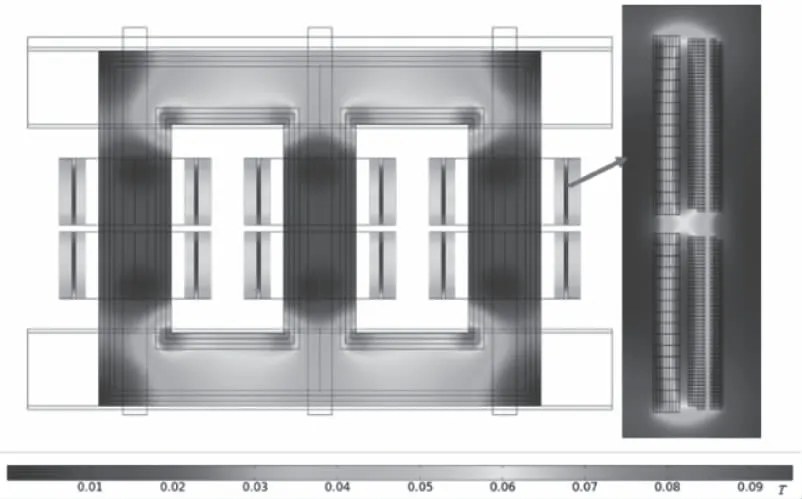
图3 磁场密度分布

2.3 损耗计算

变压器损耗主要分为铜损耗、铁芯损耗和杂散损耗。铜损耗主要为绕组电流产生的电阻热损耗，以及由漏磁通与结构件作用产生的杂散损耗，可由式(3)、(4)计算。铁芯损耗主要为铁芯材料的磁滞损耗，可由式(5)公式计算。

(3)

J=σE+jωD+σv×B+Je

(4)

P=k·fa·Bb

(5)

式中：LR表示阻性损耗，J表示电流密度，σ表示材料的电导率，E表示电场强度，D为电位移矢量，Je为外部电流。P表示单位体积铁芯磁滞损耗，f和B分别表示频率和磁感应强度，k、a、b为Steinmetz系数，此处k=100、a=1、b=1.6，本文所取铁芯材料的BH曲线如图4所示。

图4 铁芯材料BH曲线

3 损耗计算结果分析

3.1 铁芯损耗及模型验证

在开路条件下，利用本文搭建的有限元模型计算了铁芯损耗，如图5所示，磁场强度和磁通密度分布趋势基本吻合，在靠近线圈的拐角磁场强度(5×103A/m)和磁通密度(2.5 T)较大，但仍处于线性区内，而在铁芯的外圈的四个拐角磁通密度较小，约为0.5 T。如表2所示，本文计算模型所得铁芯损耗约为1.54 kW，试验结果为1.59 kW，误差为2%，相对于传统的经验计算方法有较大的改善，同时证明了本文所搭建模型的准确性。

图5 铁芯的磁场强度(左半边)与磁通密度(右半边)

表2 结果对比

3.2 杂散损耗

杂散损耗是变压器损耗计算的关键部分，由漏磁通与金属构件相互作用产生涡流从而引起涡流损耗，其主要分布在固定结构件与油箱壁。如图6所示为变压器面电流密度分布情况，固定夹件面电流主要分布绕组侧的上下两个端面上，最大值约为5.81×103A/m；由于金属夹件的屏蔽作用，油箱壁面电流主要分布在与绕组齐平的表面上，最大值最为7.36×102A/m，而在油箱壁上下两面和拐角处面电流密度较小。

图6 电流密度分布

图7 变压器夹件内侧面杂散损耗分布

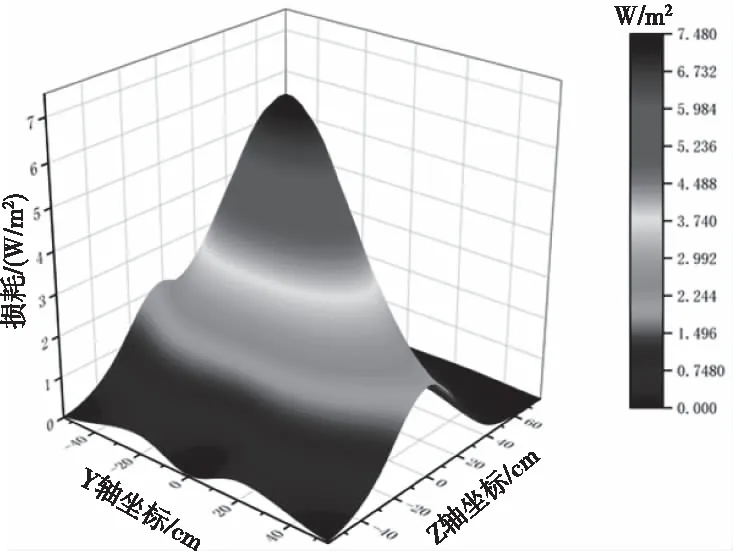
图8 变压器油箱壁侧面杂散损耗分布

图9 变压器油箱壁背面杂散损耗分布

图10 变压器油箱壁底面杂散损耗分布

如图7～图10所示为固定夹件内侧和油箱壁的损耗分布，夹件的内侧面包含上下四个面，且各个面损耗分布规律基本相同，损耗主要集中在贴近线圈的边缘附近，最大值约为20.6 W/m2；在变压器油箱壁的侧面，损耗分布整体呈现为抛物面形状，最大值出现在中心区域约为7.48 W/m2；在变压器油箱壁的背面，损耗分布整体呈现为“驼峰”形状，在油箱壁背面的左右两侧分别包含损耗的两个极大值峰，最大值约为2.47 W/m2，而在中心区域则是损耗的波谷区；在变压器油箱壁的底面，损耗分布包含一个极大值峰出现在中心区域，最大值约为1.44 W/m2，和两个较小的峰分布在两侧，周边区域损耗值较小。

3.3 铜损耗

铜损耗为绕组电流流经导体产生的热损耗。在变压器中，绕组处在复杂的电磁环境中，由式(4)可知，电流密度的分布收到磁场等多方面的影响，线圈内部电流分布并不均匀。如图11所示，在低压绕组中，单匝线圈包含4根平行导体，电流分布整体偏向于高压侧和绕组两端方向，而在高压侧电流分布主要偏向于低压侧和绕组两端方向。由此所产生的损耗分布如图12所示，分布趋势与电流密度的分布基本吻合，趋近于高压绕组之间的夹缝和绕组两端方向。

图11 绕组内电流密度分布

图12 绕组内损耗分布

4 结论

本文依据有限元理论设计了三项电力变压器的损耗计算模型，相对传统的方法，不仅能够更为准确地计算变压器各项损耗数值，同时还能够对变压器内涡流和损耗的分布规律与特征进行分析，得到的结论如下：

1)基于有限元法，提出了一种基于2D与3D模型匹配的变压器损耗混合模型，能够很好的解决变压器建模的空间尺度问题，在降低计算量的同时兼有计算的准确性。

2)变压器内部固定夹件的杂散损耗主要分布于夹件的内侧面，并集中于靠近线圈的边缘，最大值约为20.6 W/m2，在油箱壁侧面、背面和底面损耗分布呈现抛物面形、“驼峰”形和“三峰值”形。

3)高低压绕组损耗分布趋势与电流密度的分布基本吻合，整体绕组和导体内部损耗分布趋近于高压绕组之间的夹缝和绕组两端方向，对于变压器绕组的热点计算和变形评估具有一定的指导意义。