基于改进A*算法的移动机器人路径规划

汪四新，谭功全，蒋 沁，苏 畅

(四川轻化工大学自动化与信息工程学院，四川自贡643000)

1 引言

移动机器人首先要解决的问题就是如何有效快速地到达目标点，而且能够避开环境中的障碍物。路径规划是机器人导航中最基本的问题[1-2]，指的是如何规划出一条由出发位置到目标位置的无碰撞适宜轨迹。路径规划分为局部路径规划和全局路径规划[3]，局部路径规划指的是环境未知情况下的避障运动规划，全局路径规划则是在环境已知的情况下搜索全局最优的路径规划。常用的局部路径规划算法有动态窗口法DWA[4]、人工势场法[5]等。常用的全局路径算法主要有神经网络[6]、遗传算法[7]、栅格法[8]、A*算法[9]、RRT[10]以及仿生群搜索算法[11-12]等。

A*算法作为常用的全局算法中的一种，能够在静态环境中快速求解最优路径[13]。王淼弛[14]对双向A*算法采用24领域扩展方法，提高了算法单步搜索区域，但搜索节点过多且双向搜索采用异步双向搜索，导致算法的运行时间过长。王中玉等人[15]针对路径冗余点和拐点改进评价函数，提高了路径的平滑性，但采用扩展障碍物方法没有从根本上解决拐点碰撞问题。陈若男等人[16]采用领域矩阵方法搜索障碍物，改善了路径安全性，但没有提高路径搜索效率。

本文在已知静态环境下，采用A*算法双向搜索方式，并引入双向中点虚拟目标点引导双向往点靠拢相遇，减少搜索时间。其次加入预估函数权重，兼顾搜索效率与路径距离质量。最后考虑安全性，进行障碍物拐点领域扩展切换。通过仿真，验证了算法改进的有效性。

2 传统A*算法

2.1 环境建模

移动机器人进行路径规划的首先要对地图环境进行建模，环境地图目前使用较多的大概三类，分别为栅格地图、拓扑地图、可视地图。栅格地图具有易编程、结构简单等特点，因此A*算法采用栅格法进行环境建模。建立边长为k个栅格单元长度的正方形地图，即栅格地图面积为k2。完成栅格地图的框架建立后，需要对地图进行信息填充，在此之前需要确定出栅格地图中每个栅格单元的坐标位置。定义全局栅格信息为Φ，栅格地图每个栅格单元为nxy可以根据其行列坐标表示为

nxy=(x，y)(x，y∈[1，n])

(1)

式中x，y坐标起点为栅格地图左上顶点，起点值为1，x轴方向为起点垂直向下，y轴方向为起点垂直向右。

全局栅格信息Φ可表示为

Φ=∑nxy

(2)

为便于对A*路径算法的理解分析，对普遍使用的黑白栅格地图彩色化。栅格地图进行彩色化处理，需要知道对应每个栅格单元的线性化坐标，线性坐标是以栅格地图左上角为坐标起点，采用自上而下，自左往右的方式排序。因此将容易直观观察的行列坐标nxy转换为线性坐标m

m=x+(y-1)*k

(3)

式中x，y为栅格单元的行列坐标，k为地图边长。

根据A*算法需求，对线性坐标栅格进行相应颜色三元素RGB矩阵配置，分别对空地、障碍、起点、目标点、已搜索点、待搜索点、路径进行颜色矩阵设定，如表1所示。

表1 栅格地图RGB颜色配置

2.2 A*算法原理

A*算法是P.E.Hart、N.J.Nilsson和B.Raphael于1968年提出的一种启发式搜索算法。A*算法是结合Dijkstra搜索算法[17]与最佳优先搜索(BFS)算法的优点所提出的。Dijkstra算法与BFS算法都是从出发点开始，向四周发散扩展，直至搜索到目标点。区别在于Dijkstra算法是以扩展点与起点距离为代价进行路径搜索，没有考虑与目标点之间的距离关系，所以搜索出目标点花费时间很长，但搜索出的路径是最优路径。而BFS算法则相反，考虑了扩展点与目标点的关系，搜索出目标点花费时间很短，但路径不一定是最优的。A*算法兼顾Dijkstra算法与BFS算法距离代价，建立了新的搜索评价函数，如下式

f(n)=g(n)+h(n)

(4)

式中g(n)为当前点n与起点的实际距离代价，h(n)为当前点n与目标点的估计距离代价。其中代价距离均采用欧几里德距离，g(n)函数与h(n)函数计算公式如下

(5)

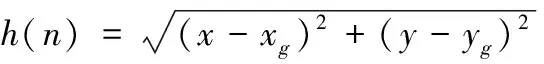
(6)

式中x、y分别代表当前扩展点的横纵坐标，xs、ys分别代表起始点横纵坐标，xg、yg分别代表目标点横纵坐标。当g(n)取值接近0时，A*算法实则变成了BFS搜索算法，当h(n)取值接近0时，A*算法则相当于Dijkstra搜索算法。

A*算法在当前点扩展领域节点时，通常采用四向、八向领域扩展，四向扩展偏向于仓储结构化的搜索方式，方向为当前点的上、下、左、右方向。八向扩展方式则是在四向扩展基础上加入了左上、右上、坐下、右下方向，扩展节点如图1。

图1 扩展节点

3 改进A*算法

3.1 双向同步搜索

改进的A*算法在传统A*算法基础上采用双向同步搜索的方式，分别将此次路径搜索的起点、目标点作为双向搜索的起点，同时向各自的目标点进行扩展，最终双向扩展点相交，终止搜索，得到全局路径。其步骤可总结如下：

1)算法运行开始时，首先创建双向OPEN表、CLOSE表、PARENT表，后标1表示正向表，后标2表示反向标，将全局路径的起始点、目标点(即双向搜索的两端点)放入对应的OPEN1表和OPEN2表，作为各自的搜索起点，准备扩展；

2)判断OPEN1表和OPEN2表是否为空。为空跳8)，否则执行3)；

3)判断OPEN1表和OPEN2表是否包含各自搜索方向目标点。包含跳7)，否则执行4)；

4)分别选取OPEN1表和OPEN2表中f(n)值最小值点存入对应CLOSE表，成为新的扩展当前点；

5)将新的扩展当前点，扩展领域范围内的点存入OPEN1表和OPEN2表中，更新其父指针，存入对应正反向PARENT表；跳过障碍物点与CLOSE表中的点扩展其它点，并跳至2)。若已存在于OPEN表中的点，则比较其评价函数的当前值与过去值，若低于过去值则刷新父指针；

6)判断正反向扩展点是否存在交集。存在交集则执行7)，否则跳2)；

7)已找到路径，连接正向父指针PARENT1与颠倒的反向父指针PARENT2，获得路径；

8)程序运行结束。

因为双向A*算法，在范围过大时往往存在双向搜索不能再地图中间区域相遇，导致搜索所花费的时间加长，甚至会出现无法相遇的情况，无法得到一条可行路径。针对以上双向搜索相遇问题，以人工势场法[18]牵引力思想，将目标点看作对移动机器人的引力作用，从而引导机器人往目标点启发式搜索。建立一个两端点欧式距离中点位置的虚拟牵引点如图2。

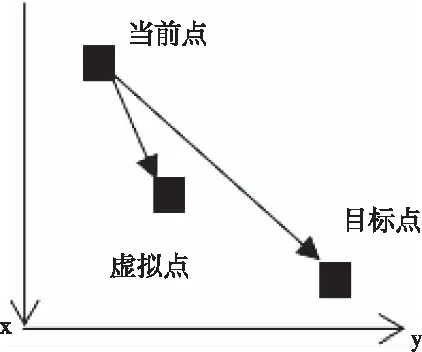
图2 虚拟牵引

虚拟点为双向搜索提供一个往中间点位置的虚拟牵引力作用，使得二者能在可行路径条件下，尽可能相遇在中间位置，缩短搜索时间，提高双向搜索的效率，如下式(7)、(8)

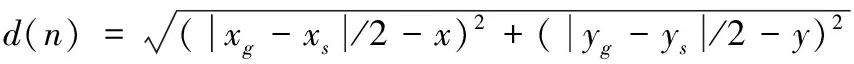
(7)

h′(n)=ln(d(n))*h(n)

(8)

式(7)中d(n)为虚拟牵引点与机器人当前点的欧氏距离，式(8)中h′(n)为加入虚拟牵引点牵引后的预估函数，其中虚拟引力点作用大小随着与双向搜索当前点距离缩短而减小，加入对数函数使得整个距离衰减过程更加平滑。

3.2 改进预估函数

对评价函数中加入虚拟引力点作用后的预估函数h′(n)加入权值函数，从而改变预估函数在整个评价函数中的比例，减少了算法搜索中无效搜索区域，提高算法的搜索效率。权值函数采用当前点与目标点欧几里德距离的衰减对数函数，加入权值函数的预估函数h″(n)如下式(9)

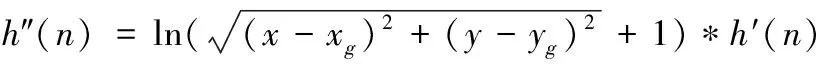
(9)

式中加入的对数权值函数随着机器人当前位置与目标点的距离变化而变化，当机器人与目标点距离很远时，预估距离要比真实距离小得多，因此权重函数值应较大，加快搜索趋近目标点速度。接近目标点时，预估距离则接近真实距离，权重函数值接近于1。

3.3 避障策略

在障碍物环境下，以机器人为栅格单位，会出现在仿真路线可行的情况下，实际机器人会与障碍物则会碰撞的安全问题，本文不考虑机器人与障碍物擦边的情况如图3。

图3 避障扩展

图3中灰色栅格为机器人当前位置，黑色为障碍物，绿色为目标点位置，此时采取8向领域扩展机器人的下一位置则是5号栅格，仿真路线可行，但实际机器人则会与障碍物发生碰撞。针对此类障碍物拐角点碰撞问题，采用领域扩展切换的方式。在进行扩展时，判断是否会出现此类问题，如果会出现则将下一步扩展由原来的8向领域扩展切换为4向领域扩展，待下一步扩展完成后在恢复到原来的四向扩展，这样就可以有效解决机器人在障碍物拐角碰撞问题。

4 仿真分析

为了验证本方法的有效性，在Matlab R2017b仿真平台下，进行了不同环境的仿真。并且通过彩色地图进行显示，各颜色表示信息如表1，能够更直观表达出改进算法的效果。

实验一首先对传统A*算法进行改进，引入双向搜索A*算法，分别将起始点和目标点作为各自的起点开始搜索，往各自目标点搜索，仿真如图4。

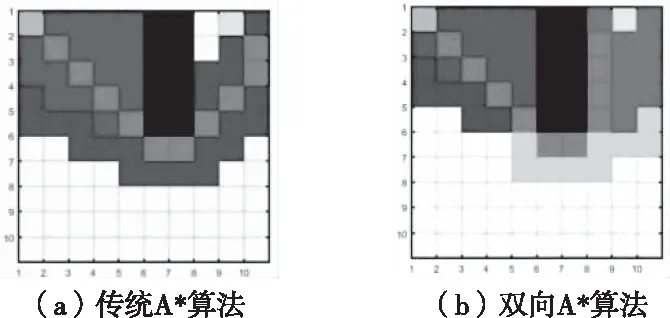
图4 实验一传统A*算法和双向A*算法仿真

图4中灰色表示机器人的最终搜索到的路径，可以看出改进后的双向搜索在路径长度上更短，通过搜索时间、长度数据更为详细地比较传统A*算法与双向A*算法见表2，引入双向搜索后的A*算法搜索时间得到了显著缩短，且路径长度也得到的略微缩短改善。

表2 实验一仿真结果数据

由于实验一栅格地图为10*10，不能暴露出双向A*算法可能出现的问题，且搜索区域较小，实验二在双向A*算法基础上，扩大栅格地图，建立30*30栅格地图，并增加起始点与目标点之间的障碍物，将传统A*算法与改进方法进行对比，仿真结果如图5。

图5 实验二传统A*算法和改进A*算法仿真

实验二在扩展的地图中，分别对传统A*算法和本文逐渐改进后的算法进行了对比仿真，对比各自算法搜索的时间、路径长度及避障性能指标来进行分析。实验二各算法仿真结果数据见表3，在扩大了地图面积并增加了障碍物后，通过与传统A*算法对比，单纯的双向A*算法如图5(b)虽然在路径长度上提升了4.4%，但在搜索时间上花费严重，增高了42.6%，原因是地图中间巨大的障碍物使得双向搜索久久不能相遇。通过引入两端点中部虚拟引力后如图5(c)，使得双向搜索即使在有障碍物影响下，也能尽快相遇，较传统A*算法搜索时间降低11.6%，路径长度降低4.9%，较单纯双向A*算法搜索时间更是降低了38.0%。在此基础上再引入衰减距离对数函数加权后如图5(d)，在保障了路径长度前提下，较传统A*算法搜索时间降低了33.5%。在改善算法搜索时间与路径长度同时，还考虑到路径可行性，即与障碍物之间的安全问题，对机器人通过障碍物拐点进行安全判据，并通过领域扩展切换方式如图5(e)，有效避免了机器人与障碍物发生碰撞，提高了路径的安全性。

表3 实验二仿真结果数据

5 结论

针对传统A*算法搜索效率低，且路径长度一般不是最优问题。本文首先引入同步双向搜索方式提高搜索效率，并考虑同步双向搜索中随着地图扩大存在的长久不能相遇问题，参考人工势场法思想，引入虚拟牵引点，在确保路径长度前提下，使得双向搜索能尽快相遇。并且对预估函数加入到搜索目标点的距离衰减函数，进一步提高了算法搜索速度。此外考虑到搜索路径安全可行问题，通过改变领域扩展方式改善避障。本文最终改进方法提高了算法搜索效率，改善了搜索路径，证明了算法改进的有效性。但本文算法不是完全优于传统方法，在特殊情况下，比如起始点与目标点之间障碍物较少或者无障碍物情况下，传统方法性能还是会优于本文方法，而且没在实际机器人中进行测试，下一步将结合实用生产环境进行研究。