3D打印氧化锆复合浆体的MRT LBM流动分析
2021-11-17孙健华
孙健华,顾 海,2*,姜 杰,2,李 彬,2
(1.南通理工学院机械工程学院,江苏 南通 226002;2.南通理工学院江苏省3D打印装备及应用技术重点建设实验室,江苏 南通 226002)
1 引言
陶瓷材料已广泛应用在诸如电子、航空、艺术、建筑、生工以及化工等重要的工业领域,皆是由于此类材料具备稳定好,抗腐蚀以及耐高温等其它材料无法取代的优点,但是成形难的特点限制了它的进一步应用发展。近些年来,增材制造技术的出现为陶瓷粉末材料的成形提供一种新的思路。目前可应用于陶瓷材料中的3D打印工艺主要包括光固化成形(Stereo Lithography Apparatus,SLA)[1-3]、喷射打印成形(Ink Jet Printing, IJP)[4]、三维印刷成形(Three-dimensional Printing,3DP)[5-6]、选区激光烧结成形(Selective Laser Sintering, SLS)[7-8]、选区激光熔化成形(Selective Laser Melting, SLM)[9-10]、熔融沉积成形(Fused Deposition Modeling, FDM)[11]以及浆料直写成形(Direct Ink Writing, DIW)[12]等六类主流工艺。根据工艺复杂性,除DIW工艺外,其余四种工艺均需要依赖激光器实现成形。在目前的DIW中,陶瓷浆料的挤出普遍采用的是类似注射器形式结构,利用气压或液压进行驱动实现浆体挤出,此种结构占用体积大,结构复杂。除了此类挤出形式外,螺杆挤出形式作为一种常见形式已有效应用在流体加工、食品运输等相关领域,这里将选用此结构替换原有的挤出结构。
为了进一步分析陶瓷复合浆料在螺杆螺道内的流动,拟采用介观数值模拟方法MRT LBM对其进行仿真分析,此方法作为一种编程实现的数值分析方法,具有物理过程清晰,方便计算的优点,避免了传统的有限元方法在计算复杂流体流动时可能出现的发散情况[13-15],这里将结合MATLAB软件进行分析计算。
2 氧化锆复合浆料的制备及流变方程的建立
这里的陶瓷浆料涉及的原始粉末为纳米级的氧化锆材料,选用苯偶酰、季戊四醇三丙烯酸酯以及甲基丙烯酸甲酯作为原始溶剂,利用高速搅拌机充分混合原始溶剂后,缓慢加入氧化锆粉末,并继续使用高速搅拌机加速粉末的充分溶解,通过测定最终复合浆料的固相含量为64.9%。
为了获取氧化锆复合陶瓷浆体的流变方程,利用Rheolab MC1型粘度计进行了粘度测试试验,实验时温度为20℃,选用三种非牛顿流体模型作为备选模型,通过MATLAB拟合获得相应的相关系数R2如表1所示。

表1 三种模型拟合相关系数R2对比
结果表明,Herschel-Bulkley流体的流变方程更符合此处的模型,具体的方程为

(1)
根据Papanastasiou T C等人对非牛顿流体的介绍,对式(1)进行了变换,并获取其粘度方程为
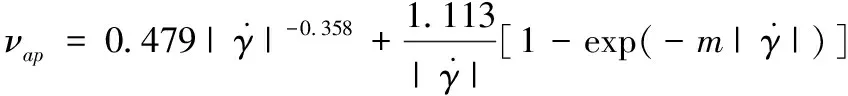
(2)
式中参数m越小时,对应的流体越接近于幂律流体,当m趋向于无穷大时,对应的流体即倾向于Herschel-Bulkley流体,这里m=600。
3 MRT LBM流动分析
3.1 单螺杆挤出结构模型
螺杆的基本结构图如图1所示,它的关键尺寸如表2所示,将其充分展开后呈现出如图2所示的腔体,氧化锆复合陶瓷浆体在原螺道内的流动即可转换成其在腔体内的流动。

图1 螺杆结构

表2 螺杆的关键几何参数

图2 螺杆展开结构
3.2 复合陶瓷浆体的MRT LBM流动分析
3.2.1 MRT LBM在非牛顿流体中的应用
多松弛时间参数的LBM与单松弛时间参数的LBM主要区别在于MRT LBM涉及到矩空间的转换[16],则其基本方程将转变为
f(r+eiδt,t+δt)-f(r,t)
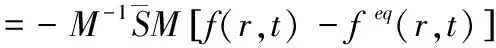
(3)
速度配置ei描述如下[17]

(4)
式中基本速度量e的大小为格子步长δx和时间步长δt的比值,通常情况下,两者均取为1,那么e=1。宏观物理量速度u,密度ρ可以根据平衡态分布函数以及格子声速获得,具体如下式所示[18]
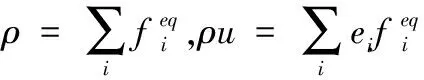
(5)
进一步地,上式中的f(r,t)和feq(r,t)两项可以通过中间变换矩阵M转换为矩空间ρ(r,t)和ρeq(r,t),具体计算公式为ρ(r,t)=Mf(r,t),ρeq(r,t)=Mfeq(r,t),其中M具体为[19]

(6)


(7)
在模型中,s0,s3,s5均是与密度和动量相关的参数,而密度和动量皆为守恒量,因此它们的值为0,s7和s8是与松弛过程相关的量,取值为1/τ,τ为单松弛参数LBM模型中的松弛时间,而剩余的参数通常取稍大于1的数即可,这里s1=s2=1.3,s4=s6=1.1。在使用MRT LBM进行流体分析时,其基本过程主要由碰撞和迁移组成,其中迁移步的表达形式为
f(r+eiδt,t+δt)=f+(r,t)
(8)
其中f+(r,t)即为碰撞后的密度分布函数,碰撞步与单松弛参数的LBM不同,具体方程为[20]
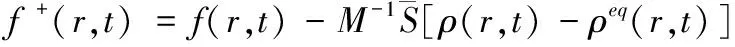
(9)
在MRT LBM中,应变率张量比单松弛参数LBM复杂,可以推导得到

(10)
应变率张量的第二不变量DII可以描述为
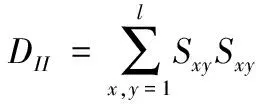
(11)
非牛顿流体的动力粘度主要与松弛时间τ和密度ρ相关

(12)
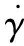

(13)
在利用MRT LBM进行实际模拟计算时,其主要过程描述如下[17-20]:
1)确定物理模型的主要基本参数,如计算域,初始速度或压力值,密度等;
2)根据式(3)计算并确定平衡态分布函数;
3)根据式(10)计算应变率张量;
4)结合式(5)和式(12),以及非牛顿流体的本构模型可以计算获得当前计算循环步内的松弛时间τ;
5)碰撞步和迁移步计算,主要参考式(8)和(9)。
6)边界处理这里主要选择非周期性边界条件;
7)根据式(5)计算密度和速度;
8)返回第3)步执行下一次循环计算。
3.2.2 复合陶瓷浆体的流动分析
取图2中的Y-Z组成的截面,根据螺杆挤出的实际运动,将速度仅设定在与Z方向一致的上表面,根据表1中列出的螺槽的几何尺寸,设置模拟时的格子数为240×180,螺杆的转速设定为N=36 r/min,通过模拟分析可以获得如图3所示的流线图。
横截面流动区域的上侧为螺杆外筒的内壁,左右两侧分别为螺杆螺槽的两个壁面,下侧则对应螺杆杆芯的外壁,根据图3可以看出,流场的中心在 (4 mm, 4 mm)附近,其更接近于螺杆的外筒,除了沿螺道方向前进外,浆体在相邻两个螺棱内壁之间存在环流。在螺棱与螺杆外壁形成的角落里则没有明显流动存在。
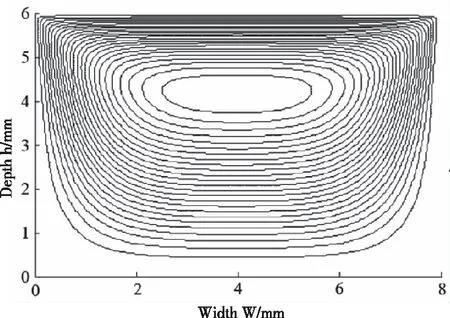
图3 浆料在Y-Z截面的流线图
在进行获取速度分布图时,为了进行对比,同时进行了格子数为160×120的MRT LBM和LBM数值分析,结果如图4-图5所示,它们的结果相近,因此可以认为本文中提出的方法是切实可行的。通过理论建模结合编程的形式实现对流体流动的研究,也为分析解决流体动力学问题提供了新的思路。图4a)和图4b)分别给出了螺槽深度h=4 mm处的度分量u和速度分量v的分布情况,明显的是,越接近于螺杆,速度分量u越大,速度分量v的极限值出现在环流中心处,而在边界处速度分量v均比较小。图5a)和图5b)分别给出了螺槽宽度W=4 mm处的度分量u和速度分量v的分布情况,速度分量u在螺棱壁面附近趋近于0,速度分量v在螺槽流道中部基本为0,逐渐往螺棱靠近时,速度也逐渐发生变化。
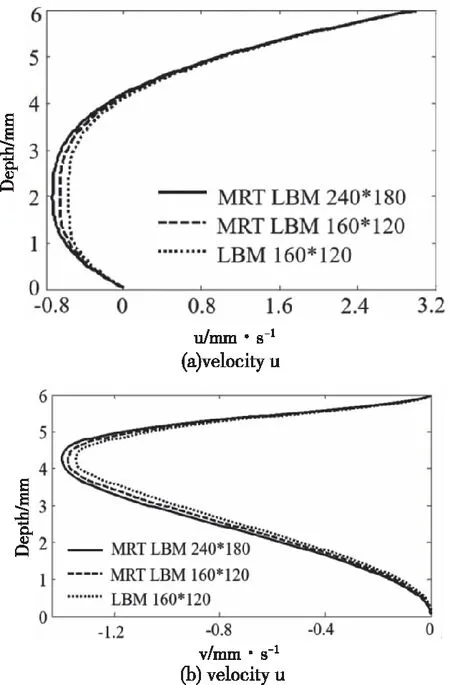
图4 速度分量沿螺槽深度的分布

图5 速度分量沿螺槽宽度的分布
4 结束语
针对陶瓷3D打印,对原有供料结构进行了改进,并利用MRT LBM对氧化锆复合陶瓷浆料在该螺杆结构中的流动进行了分析,可以获得以下结论:
1)根据流变测试结果,氧化锆复合陶瓷浆体的流变特征呈现出典型非牛顿性流体特征,与Herschel-Bulkley流体较为贴切。
2)利用MRT LBM可以有效对复杂非牛顿流体进行流动分析,编程过程简单,避免对复杂微分方程的求解。
3)对氧化锆复合浆体在挤出结构中的流动分析可知,陶瓷浆体在喷头横截面的流动呈现环流特征,环流中心大致在(0.5W,0.67h)处。结合流线图和速度分布图可以总结得知,为了保证流体的流动速度,一方面可以适当增大螺杆的旋转速度,另一方面可以适当增大螺槽的宽度。
