横向载荷作用下螺栓连接松动过程仿真研究

江文强，墨 泽

(华北电力大学机械工程系，河北 保定 071003)

1 引言

常见的螺栓连接采用普通螺栓抗剪连接，由于螺栓预紧力较小，且连接件与被连接件之间存在构造间隙，因此被连接件之间极易发生相对滑动。针对螺栓连接节点的力学性能，学者们对螺栓连接的滑移[1]、连接刚度[2]以及不同工况下螺栓连接节点的强度[3-5]等进行了研究。然而这些研究主要针对螺栓连接节点的静力学性能，即使实际载荷工况为动态载荷时也常常将其等效为静力载荷来处理[6]，显然有时这不能代表动态载荷的全部作用效果。

横向载荷作用下螺栓连接的松动常常表现为螺母与螺栓杆的相对转动。在相同的预紧力作用下，拧紧螺母所需的力矩大于螺母松退时的力矩，从而不少学者认为该力矩差是造成螺栓连接松动的原因[7-8]。同时，螺栓在动态载荷下接触界面之间的磨损[9]以及螺纹面摩擦副之间的局部变形[10-11]也会导致 螺栓连接的松动。于是部分学者针对螺栓松动的影响因素和螺栓松动的临界载荷进行了理论和实验研究，为螺栓松动的分析提供了相关参考[12]。

本文在前人研究的基础上，建立考虑螺纹的螺栓连接节点模型，采用有限元仿真分析的方法，对螺栓连接松动过程进行分析，研究影响螺栓连接松动的参数，揭示其对螺栓松动的影响规律。

2 螺栓连接节点有限元模型

如图1所示，目前研究较多的螺栓连接结构为螺栓连接两被连接件，即单肢螺栓连接。然而在一些承载较大的主要连接节点常采用双肢搭接，此时螺栓连接结构较为复杂，螺栓松动对结构的承载往往有较大的影响。

图1 常见螺栓连接结构

为此，本文根据双肢搭接螺栓连接节点的特点建立了如图2所示的螺栓连接节点模型。

图2 节点简化模型

连接板的弹性模量为206GPa，泊松比为0.3，密度为7850kg/m3，螺栓为6.8级M12×40标准六角螺栓。在有限元分析过程中采用多线性模型模拟实际材料的应力应变的变化过程。在接触对设置上，将螺栓以及中间的连接板设为接触面，其余为目标面。所有实体模型采用三维20节点Solid 186单元，其有限元模型如图3所示。

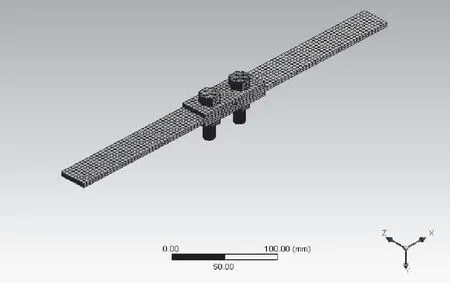
图3 有限元模型

为了分析不同接触参数对螺栓连接滑移过程的影响，以常用螺栓接触摩擦系数介于0.15～0.25之间作为参考，本文建立了如表1所示的9种模型，分别将螺母与连接板，连接板与连接板，螺栓与螺母以及螺栓杆与连接板的摩擦系数设为0.15、0.20、0.25。本文所施加的螺栓预紧力为25kN。

表1 不同摩擦系数组合

对螺栓连接节点左端固定，右端施加位移约束，载荷方向沿图示x轴正向。为了后续说明的方便，将左侧螺栓命名为螺栓A，右侧命名为螺栓B。如图4所示，分析过程中共施加10个周期的循环位移载荷，为了加载过程保证两个螺栓能够受剪，位移幅值设置为3.3mm。

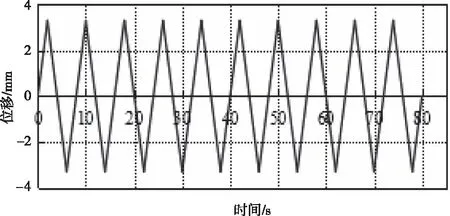
图4 位移时程图

3 螺栓连接松动过程仿真

根据有限元模型和约束条件对螺栓连接节点的松动过程进行仿真，下面对结果进行讨论。

3.1 载荷-变形过程

图5为9种模型的载荷-位移曲线，可以看出模型5的滑移载荷明显高于其它模型。对比表1中模型参数，模型5对应的连接板之间的摩擦系数最大，可见该部位的摩擦系数越大，滑移载荷也越大。

对比图5中模型1、2、3可以发现，随着螺栓与连接板间摩擦系数的增大，载荷-位移曲线变得越加饱满。对比图5中模型1、4、5的载荷-位移曲线，可以看出随着连接板间摩擦系数的增大，曲线形状也明显变得饱满，且变化程度要明显大于模型1、2、3。可见改变连接板间摩擦系数对载荷-位移曲线的影响要远大于改变螺栓与连接板间的摩擦系数的影响。对比图5中模型1、6、7、8、9可以看出，其载荷-位移曲线变化不大，可见改变螺栓与螺母之间、螺栓杆与连接板之间的摩擦系数对载荷-位移曲线几乎没有影响。

图5 螺栓连接节点的载荷-位移曲线

如图6所示为模型1在1s和2s时刻的位移云图，其它模型计算结果与此类似，这里不再赘述。图6(a)可以看出在1s时，中间连接板首先发生滑移。随着载荷增大，如图6(b)，在2s时上下连接板也相继发生滑移，螺栓B的位移明显增加。可见对于双剪切螺栓连接节点，会存在明显的二次滑移过程。从图5(a)第一周期的载荷-位移曲线可以看出，第二次滑移的载荷为第一次滑移载荷的2倍。

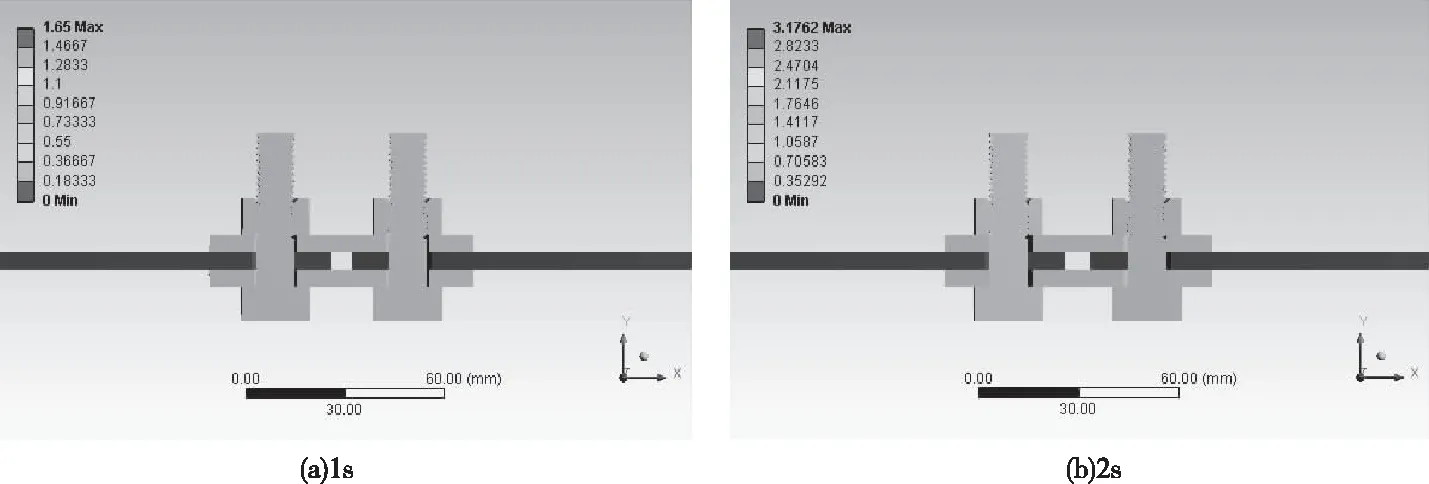
图6 位移云图(模型1)

3.2 螺栓预紧力变化过程

为了直观地分析横向载荷作用下螺栓预紧力的变化情况，绘制9个模型的螺栓预紧力随时间的变化曲线如图7所示。

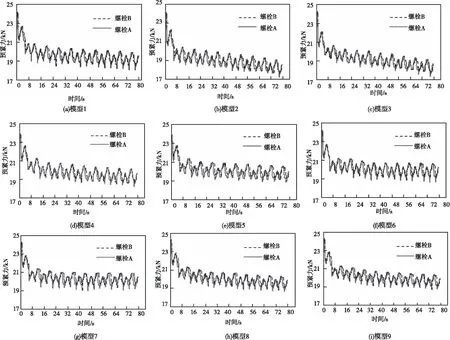
图7 螺栓预紧力时程曲线

如图7所示，在前期螺栓预紧力降低较快，后期则呈现出周期性降低的特点，因此可以将螺栓预紧力的松动过程分为两个阶段来处理。显然，不同模型螺栓松动的两个阶段变化规律也不尽相同。与此同时，两个螺栓的预紧力变化过程基本一致，所有模型的螺栓预紧力都是周期性变化的，且变化周期都与外载荷周期相同。以图7(a)中第一个加载周期为例，在0～2s节点受拉，随着横向位移的增大，螺栓预紧力逐渐减小；在2s～4s节点反向受压，随着横向位移逐渐减小，螺栓预紧力逐渐增大；此后4s～6s节点继续受压，此时螺栓预紧力开始减小，当节点达到横向位移最小值时，螺栓预紧力也减小到该载荷周期内的最小值；在6s～8s节点反向受拉，螺栓预紧力又开始增加，当节点回到原始位置时，螺栓预紧力也增加到新的峰值。一个循环周期后螺栓预紧力的峰值和谷值都逐渐减小，也就是螺栓预紧力减小，螺栓出现了松动现象。

3.3 螺纹接触状态分析

如图8所示为螺栓B在0s、2s、4s和6s时刻的螺纹接触状态，分别对应了第一个载荷周期内的初始、最大拉力、平衡位置以及最大压力四个状态。图中红色代表接触处于附着状态，橙色代表滑动状态，其上部为螺母支撑面。

图8 螺母螺纹接触状态(螺栓B)

在0s时节点处于预紧状态，无横向载荷作用。此时靠近螺母支撑面的上部螺纹接触面出现局部滑移，而下部螺纹接触面依然处于附着状态，这会使得螺栓杆产生扭转变形。螺栓杆存储下来的这部分变形能在螺栓松动的初期会快速释放，使得第一个循环周期螺栓预紧力出现快速下降的现象。

在2s时，横向载荷沿x轴正向，且处于最大拉力状态。螺纹靠近支撑面的第一圈螺纹x轴正向侧出现了局部滑移现象；在4s时，节点回到平衡位置，螺纹无明显滑移现象；在6s时，横向载荷沿x轴负向，且处于最大压力状态。螺纹靠近支撑面的第一圈螺纹x轴负向侧同样出现了局部滑移现象。由此可见，在一个载荷循环过程中，靠近螺母支撑面的螺纹发生了整体滑移，由此产生的变形以应变能的形式存储起来，并随着时间的积累逐渐向下部螺纹进行扩展，从而导致螺栓预紧力减小。

4 参数影响讨论

图9为每个载荷循环后螺栓预紧力与循环次数的关系。本节将所有模型分为四组进行讨论，第一组：模型1、2、3；第二组：模型1、4、5；第三组：模型1、6、7；第四组：模型1、8、9。

图9 螺栓预紧力-循环次数关系

通过第一组模型的比较可以发现，随着螺母与连接板之间摩擦系数的增加，螺栓松动第一阶段螺栓预紧力的衰减速度会增加。在螺栓松动的第二阶段，随着螺母与连接板之间摩擦系数从0.15增加到0.2，螺栓预紧力的衰减速度急剧增大，但当摩擦系数超过0.2以后，衰减速度几乎不再增加。

通过第二组和第四组模型的比较可以发现，随着连接板间摩擦系数或螺栓杆与连接板间摩擦系数的增加，螺栓松动第一阶段螺栓预紧力的衰减速度略有减小。在螺栓松动第二阶段各自的三个模型衰减速度均相差不大。

通过第三组模型的比较可以发现，随着螺纹接触面之间摩擦系数的增加，螺栓松动第一阶段螺栓预紧力的衰减速度显著减小。在螺栓松动第二阶段，随着螺纹接触面之间摩擦系数从0.15增加到0.2，螺栓松动现象显著降低，但当摩擦系数超过0.2以后，其对螺栓松动的影响就显著减小。

表2所示为循环加载完成后螺栓的残余预紧力及其减小幅度。从表中可以看出，模型2、3的螺栓预紧力的减小幅度最大，即螺母与连接板之间摩擦系数对螺栓松动的影响最大。模型6、7螺栓预紧力的减小幅度最小，即螺栓与螺母之间摩擦系数的增加使得螺栓预紧力减小幅度降低。模型1、4、5、8、9的残余预紧力差别不大，即连接板之间以及螺栓杆与连接板之间摩擦系数对螺栓松动影响不大。

表2 循环结束后螺栓预紧力

5 结论

本文以横向循环载荷作用下双肢搭接的螺栓连接结构为研究对象，建立了节点的精细化有限元模型，通过分析研究了不同参数条件下螺栓的松动特性，主要研究结论如下：

1)在横向载荷作用下，双肢搭接螺栓连接存在两次滑移现象，连接板之间的摩擦系数对节点的载荷-位移曲线影响最大，且该部位摩擦系数越大，载荷-位移曲线越饱满。

2)在横向循环载荷作用下，第一阶段螺栓预紧力会迅速下降，而第二阶段则主要呈现周期性衰减。

3)螺栓预紧力降低从靠近螺母支撑面的第一圈螺纹开始，并随着横向循环载荷的作用，逐渐向下部螺纹进行扩展。

4)增大螺母与连接板间摩擦系数，螺栓松动显著加快；螺纹接触面间摩擦系数的增大对防止螺栓松动有利，会大大降低螺栓预紧力的衰减速度。连接板间以及螺栓杆与连接板间摩擦系数对螺栓松动的影响相对较小。