撞击起爆中EFP模型等效的可行性仿真分析

林建清，郑 宇

(1.江南机电设计研究所，贵州贵阳 550009；2.南京理工大学智能弹药实验室，江苏南京210094)

1 引言

EFP战斗部基本原理是利用聚能效应产生的高温高压作用，将高能炸药在爆轰时释放出的化学能转化为药型罩的动能和塑性变形，使金属药型罩锻造成所需形状的高速EFP，从而以自身的动能侵彻目标，并且因其对炸高不敏感、侵彻后效作用大已广泛应用于反装甲武器系统中。近年来，国内外学者将EFP战斗部应用于防空反导中，为了解决单个EFP对分布密度小、毁伤效率低，多爆炸成型弹丸(Multiple Explosively Formed Penetrator，MEFP)的研究也开始兴起。在对EFP或者MEFP侵彻穿甲及撞击起爆仿真研究过程中。当药型罩采用拉格朗日网格建模，则药型罩网格在成型过程就已经经过大变形，再进行侵彻或撞击起爆，使得网格畸变，仿真难以计算下去。因此伍俊等人[1]将EFP成型及侵彻分成两个过程进行数值模拟；王雅君等人[2]在EFP水中飞行特性及侵彻研究中将EFP简化为圆头空心飞弹。当药型罩采用欧拉网格建模，聚能装药在成型中及侵彻过程采用ALE算法[3-5]，则在仿真过程不能利用重启动，并且在研究MEFP各个药型罩之间的距离对撞击起爆的影响时，需要重新建模，大大增加了仿真周期。

为了解决上述这些仿真问题，本文利用Ls-Dyna数值仿真软件，综合考虑了头部形状、尾裙、实心部长度以及质量的等效，继而对EFP及等效EFP的侵彻能力及撞击起爆能力进行仿真研究，并分析两者等效的可行性。

2 仿真计算方法

EFP的成型过程具有大变形、高应变率、高过载的特点，仿真过程会造成网格严重畸变导致计算无法进行。为解决网格畸变导致计算无法进行的问题，本仿真计算模型由炸药、药型罩、空气、钢锭(或盖板、被发炸药)，其中炸药、药型罩和空气采用欧拉网格建模，使用多物质ALE算法，钢锭(或盖板、被发炸药)采用拉格朗日网格建模，并且钢锭(或盖板、被发炸药)与空气和药型罩之间采用流固耦合算法。在等效EFP和钢锭(或盖板、被发炸药)模型时采用拉格朗日网格建模，在计算过程中，等效EFP与靶板之间采用自动面面侵蚀接触。仿真计算中各部分的材料模型及状态方程见表1所示。

表1 仿真材料模型及状态方程

3 EFP成型及仿真模型等效

3.1 EFP成型

本研究采用的是40mm口径的聚能装药，药型罩采用弧锥结合形结构，装药采用8701炸药，成型装药为1/4三维数值仿真模型，如图1所示。

图1 40mm口径成型装药1/4结构图

成型装药采用中心点起爆方式，在起爆100 μs后EFP基本趋于稳定飞行，其整体速度大约为1480 m/s，其中Vh为头部平均速度，Vt为尾部平均速度，其成型过程EFP轴向头、尾速度变化曲线如图2所示。

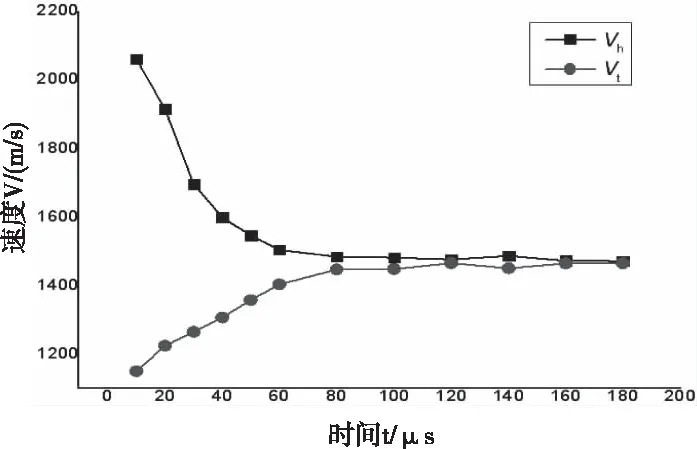
图2 EFP成型过程头尾平均速度变化图

3.2 EFP模型等效

为解决由于聚能装药成型的EFP和MEFP几何结构不容易控制，以及在侵彻、撞击起爆仿真中网格畸变导致的计算时间变长、计算精度下降等问题，将成型后的EFP进行等效建模，由于EFP头部形状[5]、实心部长度对撞击起爆都有影响，因此在EFP模型等效时，综合考虑了头部形状、尾裙、质量的等效。如图3所示，左图为聚能装药成型后的EFP，右图为直接等效建模的EFP。图4为等效EFP结构示意图，其中l1为EFP实心部长度，l2为EFP总长度，d1为EFP实心部直径，d2为EFP最大直径。EFP等效前后结构参数见表2。

表2 EFP等效前后模型参数

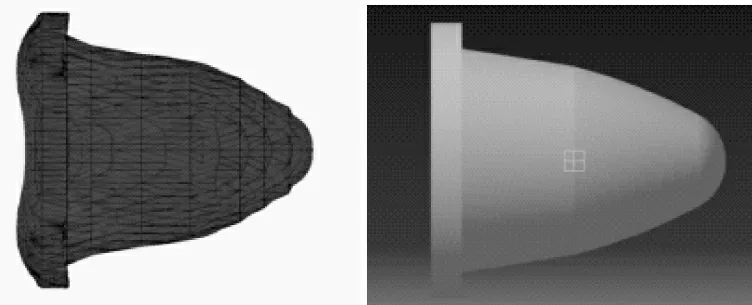
图3 聚能装药成型EFP和等效EFP

图4 结构示意图

4 等效前后侵彻能力及撞击起爆能力对比

在对撞击起爆中EFP模型的等效时，不但要使聚能装药成型的EFP和等效EFP侵彻威力相近，而且也要使EFP等效前后两者的撞击起爆性能相近，因此分别进行了仿真分析对比。

4.1 EFP等效前后的侵彻能力对比

为了验证聚能装药成型的EFP和等效EFP各自的侵彻威力，分别建立了聚能装药成型的EFP侵彻钢锭和等效EFP侵彻钢锭模型，其中钢锭采用45号钢，尺寸为Φ120 mm×50 mm，等效EFP材料也采用铜，对两者分别进行侵彻钢锭的数值仿真，仿真模型和仿真侵彻结果如图5所示，其中(A)图为聚能装药成型EFP侵彻模型和侵彻仿真结果，(B)图为简化EFP侵彻模型和侵彻仿真结果。

图5 侵彻钢锭模型及仿真结果图

仿真计算结果局部如图6所示，其中D1为弹坑口部直径；D2为弹坑底部直径；H为侵彻深度。将聚能装药成型EFP侵彻仿真结果与等效EFP侵彻仿真结果进行比较，如表3所示。

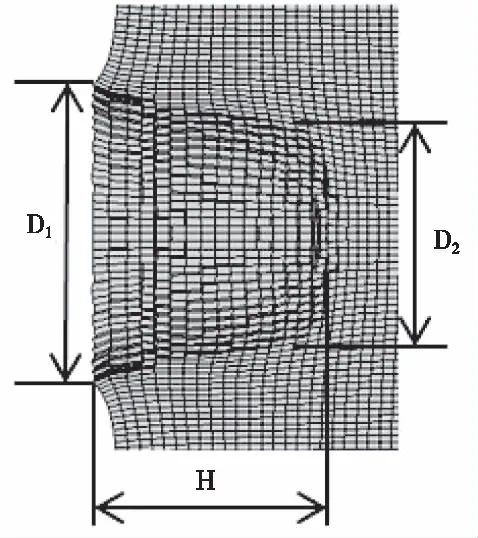
图6 钢锭侵彻结果局部图

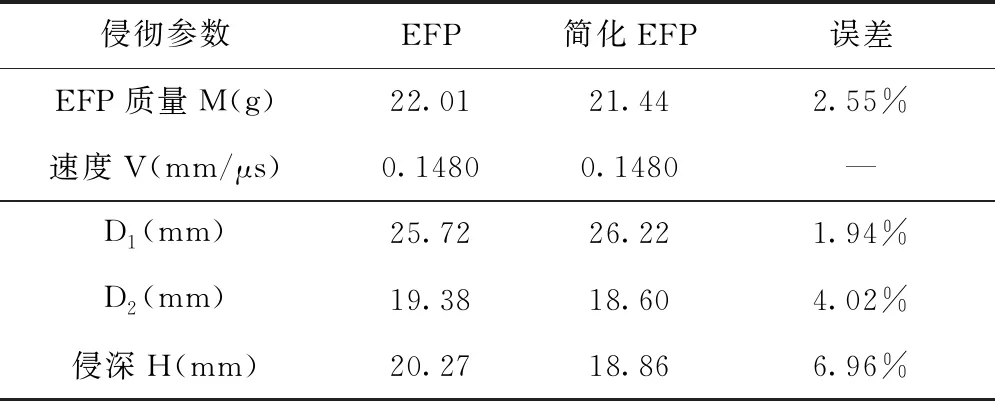
表3 EFP侵彻威力仿真结果数据

由表3对比结果可知，聚能装药成型EFP和等效EFP侵彻威力的仿真数据最小误差存在于侵彻后弹坑口部直径D1为1.94%，最大误差存在于侵彻深度H为6.96%，说明聚能成型的EFP与等效EFP的侵彻威力近似，因此在侵彻威力方面聚能装药成型的EFP可以简化为简化EFP。

4.2 EFP测速及侵彻威力试验

为了验证EFP成型及侵彻威力仿真的准确性，进行了EFP高速摄像测速试验和侵彻威力试验。

利用高速摄像技术对EFP成型过程进行测速，考虑成型装药爆炸后会出现过曝而拍不到EFP飞行轨迹，在成型装药和铝板中间放置挡光板，试验布置如图7所示。左图为试验布置示意图，右图为现场试验的实景图。

图7 EFP测速试验布置图

第一发试验由于挡光板距成型装药太近导致过曝而未测到速度，高速摄像处理软件中的测速结果见表4。

表4 EFP高速测速结果数据

侵彻威力验证所需的钢锭与数值仿真保持一致，为45#钢，尺寸为Φ120 mm×50 mm。首先将钢锭放在平地上，然后将炸高筒放置于钢锭上，最后放置硬纸板于炸药筒上，将套有雷管座的EFP竖直放在硬纸板上。试验布置如图8所示。左图为试验布置示意图，右图为现场试验的实景图。

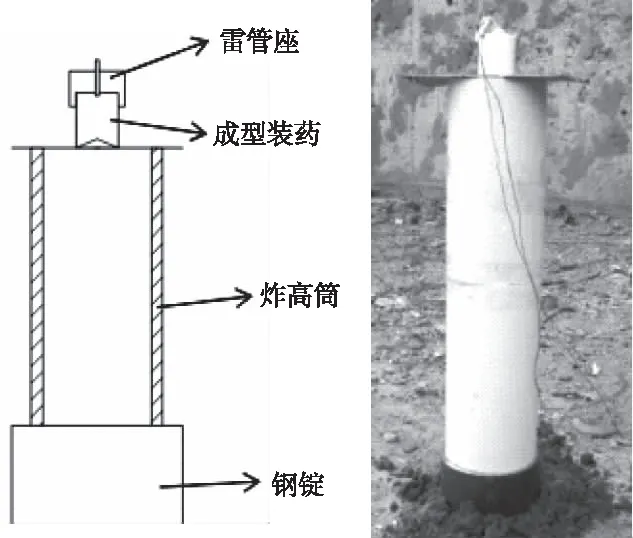
图8 EFP侵彻威力试验布置图

用游标卡尺测量出侵彻的深度H、侵彻的弹坑口部直径D1以及弹坑底部的直径D2。试验测量的侵彻数据[7]以及试验与仿真的误差见表5。其中仿真1最大误差是指：聚能装药成型的EFP侵彻结果与试验结果的最大误差；仿真2最大误差是指：简化EFP侵彻结果与试验结果的最大误差。

从表3的对比结果可知：EFP仿真得到的速度和试验得到的速度具有较好的一致性。从表5试验与仿真对比结果可知：聚能装药成型的EFP侵彻结果与试验结果的最大误差为5.67%，简化EFP侵彻结果与试验

表5 EFP侵彻威力试验结果数据

结果的最大误差为3.53%，因此EFP等效前后的仿真结果是可信的。

4.3 EFP等效前后的撞击起爆能力对比

为了说明等效后EFP撞击起爆能力的合理性，将聚能装药成型的EFP和等效EFP进行撞击起爆能力的数值仿真对比，因此本小节建立了聚能装药成型的EFP撞击起爆盖板炸药的1/4模型，如图7所示，盖板材料为45#钢，被发炸药为Comp B炸药，炸药尺寸为Φ120 mm×108 mm。图8(A)为聚能装药起爆后106μs的EFP撞击盖板炸药前的状态，EFP平均速度为0.1480mm/μs，利用“升降法”得到EFP撞击盖板Comp B炸药的临界盖板厚度；然后以106μs时EFP的速度为等效EFP的速度，撞击相同盖板厚度下的Comp B炸药，其仿真模型如图8(B)所示，同样利用“升降法”得到等效EFP撞击盖板Comp B炸药的临界盖板厚度；最后将两者撞击盖板炸药的起爆到爆轰过程进行对比。

表6、表7给出了聚能装药成型的EFP和等效EFP在撞击盖板Comp B发生爆轰和未发生爆轰的各个时刻反应压力云图。

图9 EFP撞击起爆盖板炸药数值模型

图10 EFP等效前后撞击起爆盖板Comp B

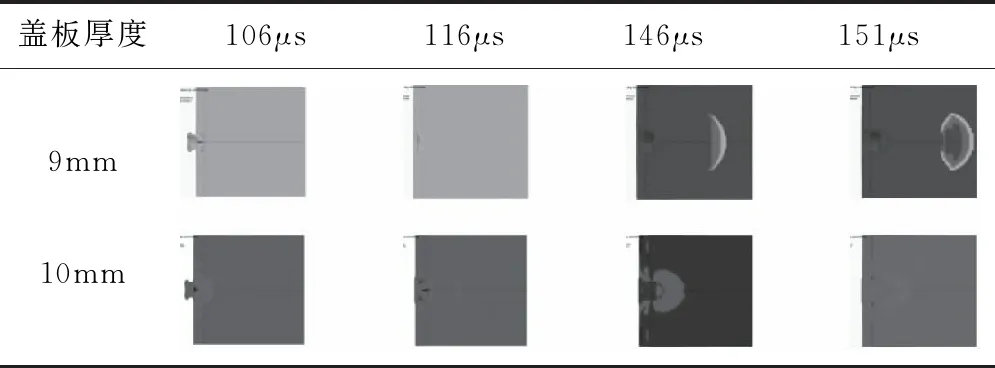
表6 EFP撞击盖板炸药压力云图

表7 简化EFP撞击盖板炸药压力云图

根据表6和表7的数值仿真结果可知：

1)对于聚能装药成型的EFP其在100μs就已经完全成型，其在106μs撞击9mm盖板Comp B时，EFP先在盖板前端面形成一定区域的压缩剪切，随着压缩剪切的进行，当到达盖板后端面附近时，主要以拉伸为主，随着侵彻进行到穿透盖板，炸药并未起爆而是继续侵彻炸药，在146μs达到起爆压力[8]5.63GPa，起爆点距离盖板95.3mm，在151μs达到CJ压力[9]29.5GPa，此时Comp B已经达到稳定爆轰；而在EFP侵彻10mm盖板炸药时，侵彻盖板过程一样，但是在侵彻进入炸药后并未发生起爆；9mm为起爆临界盖板厚度。

2)对比等效EFP在撞击盖板厚度为9mm的Comp B炸药时，其侵彻盖板过程类似，并在42μs时达到起爆压力，起爆点距离盖板88.9mm，45μs时达到CJ压力，此时炸药应该达到稳定爆轰；在撞击10mm盖板炸药时，未起爆。

两者撞击起爆过程参数见表8，其中起爆时间T1为EFP撞击盖板到炸药起爆所经历的时间，爆轰时间为T2为EFP撞击盖板到炸药达到爆轰压力的时间，起爆距离S为盖板与炸药接触面到炸药达到起爆压力的距离。

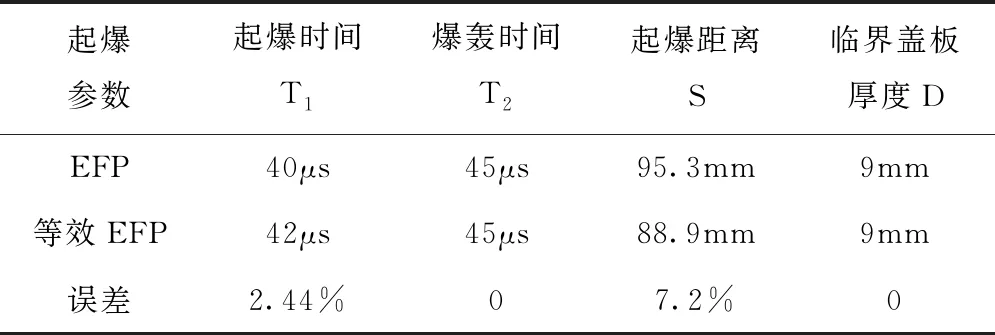
表8 撞击起爆过程参数

根据表8对比结果可知，两者撞击起爆时间误差仅为2.44%，起爆距离误差为7.2%，说明了两者的撞击起爆能力近似，因此在撞击起爆威力方面，EFP的等效是可行的。

5 结论

针对撞击起爆中EFP模型的等效的可行性，进行了EFP等效前后的侵彻性能及撞击起爆能力的数值仿真分析，根据仿真结果得出以下几个结论：

1)在综合考虑头部形状、实心部长度以及质量的情况下将聚能装药成型的EFP进行等效建模，等效后EFP的侵彻仿真威力最小误差存在于侵彻后弹坑口部直径D1，其值为1.94%，最大误差存在于侵彻深度H，其值为6.96%，说明聚能成型的EFP与等效EFP的侵彻威力近似，因此在侵彻威力方面聚能装药成型的EFP可以简化为简化EFP。

2)等效前后EFP的撞击起爆时间误差仅为2.44%，起爆距离误差为7.2%，并且撞击起爆的临界盖板厚度都为9mm45#钢，说明了两者的撞击起爆能力近似，因此在撞击起爆威力方面，EFP的等效是可行的。

3)综上所述，撞击起爆中本文EFP模型的等效是可行的，研究成果对EFP、MEFP侵彻及撞击起爆战斗部研究中的模型等效具有一定的参考价值。