基于混沌离散粒子群的粗糙集属性约简算法
2021-11-17栾雨雨王锡淮肖健梅
栾雨雨,王锡淮,肖健梅
(上海海事大学物流工程学院,上海 201306)
1 引言
随着大数据时代的到来,数据量激增。面对大量的数据,进行数据分析、分类与特征提取比较困难,需要有效的工具挖掘出数据中潜在有用的知识。数据挖掘中,属性约简是一个重要问题。属性约简是指在保持知识库分类能力不变的情况下,删除不重要或无关的属性,从而降低数据的维度,简化知识处理的过程[1]。
粗糙集理论(RST)是波兰学者Z.pawlak在1982年提出的,用来处理不确定性和不完整性信息[2]。文献[3]研究了基于粗糙集的属性约简算法,提出一种基于启发式的依赖度计算方法,提高了RS约简算法的运行速度。文献[4]提出基于模糊粗糙集的属性约简算法,设计了一种贪婪收敛的约简算法,实现了更好的性能。这些算法通常以属性重要度或其它的重要信息作为启发信息,依据一定的规则迭代运算,通常对计算有较高的要求,当数据量很大时,并不一定能得到最优子集。
为了提高RS约简算法的精度,一些学者提出将智能算法与RS算法相结合。文献[5]提出基于并行遗传算法与粗糙集的特征选择算法,减少了算法的运行时间,提高了分类器的精度。文献[6]将鱼群算法与邻域粗糙集结合,定义三种鱼群的觅食行为,以找到最佳属性子集和适应度函数来评估最佳解,该算法更有可能找到最优约简。文献[7]提出一种混合人工蜂群算法,基于不可分辨原理,对粗糙集理论中的实值属性进行约简。文献[8]提出一种结合飞蛾火焰的RS约简算法,利用飞蛾火焰的探测能力和粗糙集的高性能进行属性约简,并应用于番茄病害的检测,取得了不错的效果。
粒子群算法(PSO)是一种通过模拟飞行鸟类的行为及其信息交换方式来解决优化问题的算法,具有运行速度快、易收敛的优点,更适合于维数较多的属性约简问题。文献[9]提出基于粗糙集和粒子群的属性约简策略,并验证了该算法比基于遗传算法的约简算法有更好的性能。然而传统的粒子群优化算法容易陷入早熟现象,从而出现次优解。
为此,将混沌序列引入到粒子群优化算法。混沌是非线性系统中的常见现象,一般情况下,由确定性方程得到的具有随机性的运动状态称为混沌。混沌具有遍历性、无序性、随机性、初始条件敏感等特性[10]。通过混沌优化,可以实现全局优化。因此,基于混沌的优化更有优势。文献[11]通过引入混沌优化算法和粒子群优化算法,提出一种新的最小二乘支持向量机的数据分类方法,实验表明该方法有较好的分类能力,克服了传统粒子群的缺点。
针对传统粒子群约简算法容易包含冗余属性且容易发生早熟现象的缺点,本文提出混沌离散粒子群算法(CBPSO),应用于粗糙集属性约简问题。混沌优化算法的引入,使粒子可以向多个方向搜索,增加种群的多样性。同时改进惯性因子和加速因子,提高了算法的全局搜索能力,使种群快速找到全局最优解。实验证明,该算法可以在保持知识系统信息的条件下约简更多的属性,同时还可以提高分类精度和速度,是解决属性约简问题的有效方法。
2 粗糙集理论
在粗糙集理论中,定义一个知识表达系统S=(U,A,V,f)[12]。U称为论域,是有限的非空对象集;A是有限的非空属性集,A=C∪D,C和D分别为条件属性集和决策属性集;V=∪a∈AVa,Va是属性a的值域;f:U×A→U是信息函数,使得对∀a∈A,x∈U,有f(x,a)∈Va。
定义1[13]:给定一个论域U和U上的一簇等价关系S,若P⊆S,且P≠∅,则∩P(P中所有等价关系的交集)仍然是论域U上的一个等价关系,称为P上一个的不可分辨关系,记为IND(P),也常简记为P。而且
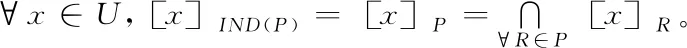
(1)
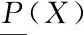
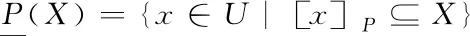
(2)
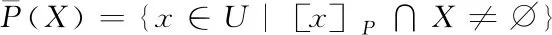
(3)
定义3[13]:在信息系统S=(U,A,V,f)中,对于每个子集X⊆U,X的P正域、P负域、P边界域定义如下
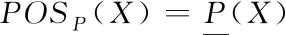
(4)
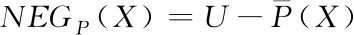
(5)

(6)
定义4[14]:在信息系统S=(U,A,V,f),(A=C∪D)中,条件属性子集B∈C和决策属性集D之间的依赖度定义如下
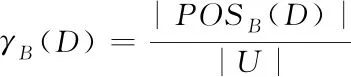
(7)
如果γB(D)=0,那么D独立于B;如果γB(D)=1,那么D完全依赖于B;如果0<γB(D)<1,那么D部分依赖于B。
3 混沌离散粒子群优化算法
3.1 离散粒子群算法(BPSO)
BPSO算法是James Kennedy 和Russell C. Eberhart为解决离散优化问题提出的的。BPSO算法中,使用Sigmoid函数将连续的位置向量映射到离散空间。设xim(t)和vim(t)表示在第t次迭代时,粒子i的第m维的位置和速度分量,pim是粒子局部最优位置pbest的分量,pgm是全局最优位置gbest的分量,粒子的速度变化和标准PSO一样,如式(8)所示
vim(t+1)=ωvid(t)+c1r1(pim-xim(t))
+c2r2(pgm-xim(t))
(8)
其中c1和c2是两个正的加速常数,通常取c1=c2=2,r1和r2是取值在[0,1]的均匀随机数。ω是惯性因子,通常根据式(9)进行设置。ωmax和ωmin分别是初始权重和最终权重,一般取ωmax=0.9,ωmin=0.4。t是当前迭代次数,T是最大迭代次数。

(9)
粒子的位置更新如式(10)、(11)所示
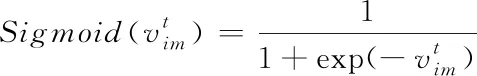
(10)
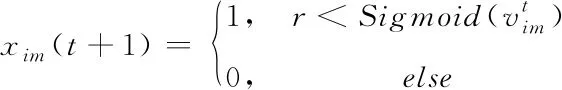
(11)
3.2 混沌离散粒子群算法(CBPSO)
为解决BPSO易早熟、陷入次优解的缺点,引入混沌序列。常用的混沌模型为Logistic 模型,数学表示为
zn+1=μzn(1-zn),zn∈(0,1),n=0,1,2,…
(12)
式中,μ表示控制参数,n表示迭代次数。当μ=4,z0∈(0,1)时,Logistic方程处于完全混沌状态。
混沌序列主要通过以下两方面与粒子群算法结合[15]。
一方面,利用混沌序列的随机性初始化粒子。通过式(12)生成一组与粒子数相同的混沌序列:Zi=(zi1,…,zim,…,ziM)。通过式(13)生成第i个粒子的连续位置变量xim。通过式(14)将位置变映射到离散空间,则Xi=(xi1,…,xim,…,xiM)对应为一个离散粒子。
xim=ximin+zim(ximax-ximin)
(13)

(14)
ximax和ximin分别为粒子位置的上限和下限。
另一方面,在种群迭代过程中,对种群最优粒子增加混沌扰动。在迭代过程中,计算每个粒子的适应度值fit(i),对fit(i)高的前30%的粒子增加混沌扰动。
通过混沌序列Zi生成新的离散粒子,计算新粒子的适应度值,用适应度值高的粒子替换原有粒子,改变粒子的搜索方向。
3.3 加速因子和惯性因子的改进
BPSO算法中,合理设置c1和c2以及ω的值可以平衡算法的全局搜索和局部搜索能力,使粒子快速地飞向最优解。
对于属性约简问题,搜索前期,需要粒子搜索更多的空间,即前期c1和ω应该较大。而在进化的后期,需要加强粒子间的信息交流以达到最优值,即后期c2和ω应该较大。因此,本文中c1、c2和ω如式(15)(16)(17)所示

(15)
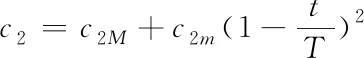
(16)
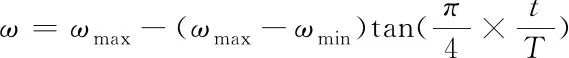
(17)
其中c1m、c1M和c2m、c2M均为固定的常数,取c1m=0.5,c1M=2,c2m=2,c2M=2.5。
4 基于混沌离散粒子群的粗糙集属性约简算法
本文采用改进后的粒子群算法,结合粗糙集理论,求解属性约简问题。设种群是一个包含所有属性子集的大的属性空间,属性空间中的每一个位置表示一个属性子集。最优位置代表分类质量最好、属性数量最少的那个子集。现在,假设数据集的条件属性个数为M,则搜索空间为M维,在搜索空间中放N个粒子,每个粒子都代表一个潜在的属性子集。粒子的目标是搜索整个属性空间,找到最优位置。
4.1 粒子位置的表示
CBPSO算法中,将粒子的位置表示为长度为M的二进制字符串,粒子位置的每一维表示一个属性,1表示选择相应的属性,0表示该属性未被选择,每个位置都是一个条件属性子集。
4.2 粒子速度限制
CBPSO算法中,粒子速度最大值vmax可以决定搜索空间的精度。本文中,vmax=(1/4)*N,且速度范围限制在[1,(1/4)*N]内。当vim<1时,令vim=1;当vim>(1/4)*N时,令vim=(1/4)*N。在这个范围内,粒子通常可以快速找到最优解。
4.3 适应度函数
本文的适应度函数如式(18)所示
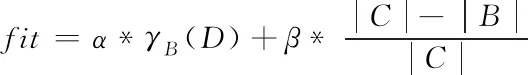
(18)
其中,γB(D)是条件属性子集B和决策属性集D之间的依赖度,|B|是选择的条件属性子集中属性的个数,|C|是条件属性的总个数。α越大,表示算法约简效果越好,越符合粗糙集的约简标准。β越大,表示删减掉的属性数目越多。本文中,α=0.8,β=0.2。设置较大的α值可以保留决策表的知识信息。每个位置的适应度值都将通过这个函数进行评估,算法的标准是最大限度的提高粒子的适应度值[16]。
4.4 算法流程
算法1基于混沌离散粒子群的粗糙集属性约简算法
输入:一个决策表S=(U,C∪D,V,f)
输出:决策表S的一个属性约简
步骤1:输入粒子个数、粒子维数、最大运行次数、速度限制、位置限制。利用logistic模型映射得到粒子初始速度和位置。
步骤2:计算粒子的适应度值fit(i)和个体最优值pbest(i),计算群体最优值gbest。
步骤3:对每个粒子,如果fit(i)> pbest(i),则令pbest(i)=fit(i);如果fit(i)> gbest,则令gbest=fit(i);并将该粒子的位置作为全局最优位置记录下来。
步骤4:更新粒子的速度vi和位置xi。
步骤5:对种群中30%的最优粒子增加混沌扰动,得到新的粒子。计算扰动后粒子的适应度值gbest’,如果gbest’>gbest,则扰动后的粒子记录为全局最优点。
步骤6 判断是否满足终止条件,若连续10次全局最优位置不变或迭代次数达到T=200时,则算法终止,输出全局最优粒子,即约简得到的属性集;否则,转步骤3。
5 实验结果及分析
本文从UCI机器学习数据库中挑选了4组数据,通过实验验证CBPSORS算法的有效性, 4组数据的基本说明见表1,其中KNN表示包含所有属性的原始数据集的分类精度。
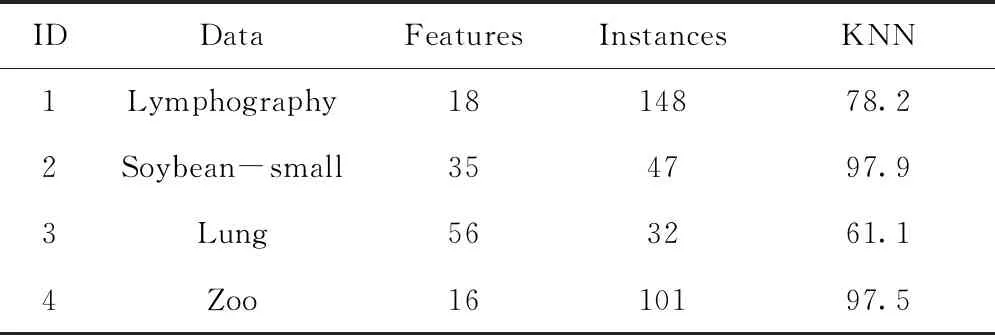
表1 实验中使用的UCI数据集
本文选择了一种基于粗糙集的属性约简算法(RS,算法2);两种基于粗糙集的智能属性约简算法:基于粒子群的粗糙集属性约简算法(PSORS)和基于遗传算法的粗糙集属性约简算法(GARS),来进行实验,这些算法参数设置见表2。并采用10折交叉验证的方法,基于k最近邻算法为每个样本生成分类模型,计算这些算法的分类精度。

表2 算法参数设置
算法2:基于粗糙集的属性约简算法
输入:一个决策表S=(U,C∪D,V,f),C={a1,a2,…,an}
输出:决策表S的一个属性约简
步骤1:计算条件属性集C的D正域POSC(D)。
步骤2:对于属性ai∈C,计算条件属性子集C-{ai}的D正域POSC-{ai}(D)。
步骤3:若POSC-{ai}(D)=POSC(D),则说明属性ai对于决策属性集D不是必要的,可以删减掉该属性,转步骤2。否则,说明属性ai不能删减,输出属性约简集C。
首先,将本文算法约简后得到的数据集与原始数据集作比较,约简前后的分类精度见表3。可以看出,部分数据集的属性约简率达94%,且分类准确率基本都有所提高。
其次,将本文算法与两种基于智能算法的粗糙集约简算法(GARS、PSOARS)进行对比,所得属性子集见表4。对于所有的数据集,本文算法都可以得到属性数量最少的子集。
最后,将本文算法与RS算法作比较,比较结果见表5。可见,在属性个数和分类精度方面,本文算法优势明显。
四种算法的比较结果见表6。对于所有的数据集,本文算法都能得到数量最少的属性子集。而且对于KNN分类器,由本文算法约简后的数据集分类精度最高。
表3至表6从不同方面体现了本文算法的优越性。说明了算法的搜索策略和属性子集相关性的评价方法影响着属性选择的结果。

表3 约简前后数据性能的比较
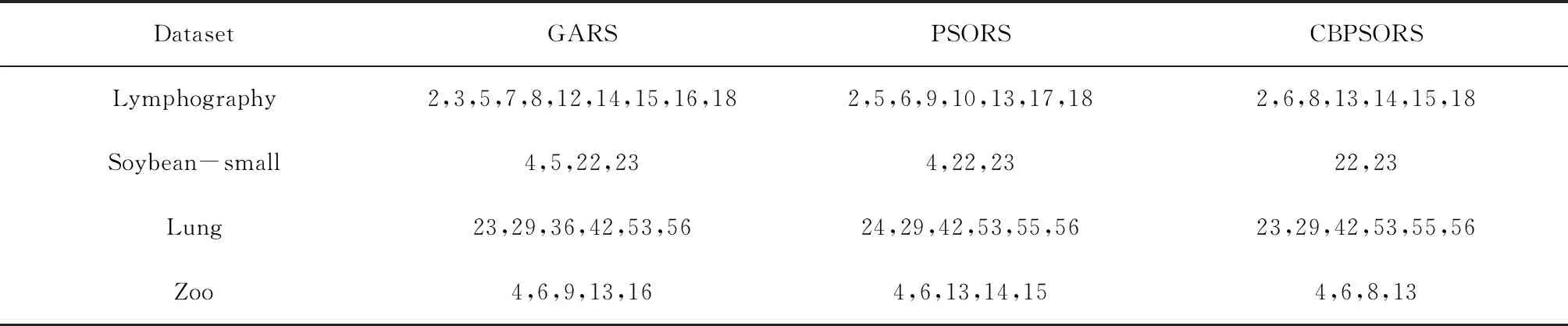
表4 三种智能约简算法得到的属性子集

表5 RS算法与CBPSORS算法的约简比较

表6 四种算法对比结果
混沌优化策略使种群的空间搜索更具多样性,属性子集的相关性评价策略使算法能找到更优的子集。实验结果表明,本文算法保留了混沌优化的优点,又克服了传统PSO算法的缺陷,可以很好地解决属性约简问题。在属性约简个数和分类准确率方面,本文算法都有明显的优势。
6 结语
本文针对属性约简问题,提出了基于混沌离散粒子群的粗糙集属性约简算法,解决了传统属性约简算法效率低的问题。该算法引入混沌优化策略,避免了传统粒子群算法陷入次优解,提高了算法的全局搜索能力。同时改进加速因子和惯性因子提高算法的运行效率。最后使用粗糙集中依赖度的概念来评估生成属性子集的相关性,通过交叉验证得到的分类精度和属性约简个数来评估算法的性能。实验结果表明,与RS、GARS和PSORS算法相比,本文算法可以提高粒子的利用率,有更好的约简能力。对于相同的数据集,本文算法能得到数量更少的属性子集和更高的分类质量。但是,本文算法是用单个函数作为适应度函数,未来可以使用多个标准来评估属性子集,发展该算法的多目标版本。
