多无人机协同干扰组网雷达的优化研究

霍跃珍，杨象驰，李杭蔚

(1.西安邮电大学经济与管理学院，陕西 西安 710061；2.西安邮电大学现代邮政学院，陕西 西安 710061)

1 引言

无人机(UAV)与载人飞机相比，具有体积小、造价低、使用方便、战场生存能力较强等优点，对未来空战有着重要的意义。而在现代战争下，世界各个国家均认识到了单部雷达作战性能上的局限性，开始大力发展组网雷达技术。攻击方如何利用无人机对其进行有效的侦查和干扰成为电子对抗界关注的重要问题。

自文献[1]首次在国内提出了通过多机协同产生假目标航迹对组网雷达进行欺骗的方法以来，关于无人机对组网雷达进行协同干扰方面的研究一直在进行。比如，通过建立二维和三维的航迹规划模型，优化求得无人机的最短飞行轨迹[2]；建立最优控制模型并采用勒让德伪谱法和可行序列二次规划软件包求解最优化问题，得出形成虚假目标的多机协同航迹[3]；根据不同无人机编队对组网雷达探测效能影响的仿真结果对无人机编队航迹进行优化[4]等。但这些研究大多关注于假目标航迹的合理性分析以及无人机协同运动的策略，实际上在无人机协同干扰组网雷达的军事应用过程中，如何通过无人机编队的路径规划产生确定假目标航迹而不再是一些随机性的轨迹，使得攻击方对敌方的欺骗效果更加显著。针对此问题，目前还鲜少有文献涉及到。本文提出了在实现一确定假目标航迹的前提下，基于蚁群算法和聚类法的无人机航迹优化模型，并以一个应用实例对其进行了仿真验证其可行性。

2 多无人机对组网雷达进行协同干扰的原理

多无人机对组网雷达进行协同干扰的基本原理是：

首先，无人机基于侦察到的敌方雷达发射电磁波的信号特征，对其进行相应处理后，延迟(或导前)一定时间后再发射出去，使雷达接收到一个或多个位于无人机与雷达直线上的，比真实目标靠后(或靠前)的回波信号。

其次，对于真目标，各雷达探测出的真目标空间状态是基本一致的，可以认为它们是源自于同一个目标(同源)；对于有源假目标，其空间状态由无人机和雷达部署位置共同决定，不同雷达量测到的有源假目标的空间状态一般是不一致的，有理由认为其来自于不同目标(非同源)，利用这种不一致性就可以在组网雷达信息融合中心将假目标有效剔除，即“同源检验”。现在，雷达将接收到的经过无人机干扰设备处理后转发回的干扰信号形成目标航迹点信息，传输至组网雷达信息融合中心。

最后，融合中心基于一定的同源检验融合规则，对接收到的多部雷达在统一坐标系的同一空间位置上检测到的目标信号，判断其是否为一个合理的目标航迹点，多个连续的合理目标航迹点就形成了目标航迹。干扰过程如图1所示。

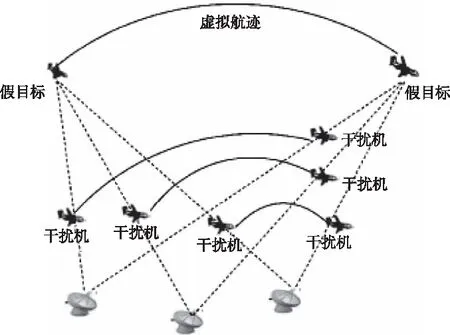
图1 多无人机协同干扰组网雷达系统示意图

3 多无人机协同干扰模型的建立

3.1 模型假设

1)假设已知雷达的位置坐标，雷达和信息融合中心接收信息时间间隔为Δt，均不存在时延。

2)假设真实目标产生的回波不能被雷达有效检测。

3)假设同一时刻一架无人机只能干扰一部雷达，但同一时刻多架无人机可以干扰同一部雷达，不考虑外界对无人机和雷达的影响。

4)假设无人机不做爬升、俯冲等机动动作，即无人机在同一高度匀速直线飞行。

5)出于安全等因素的考虑，无人机的速度范围为(vmin，vmax)，它们之间的最小间隔距离为ΔS，飞行高度范围为(hmin，hmax)。

3.2 无人机干扰模型建立

3.2.1 单机运动模型的建立

分析多无人机对组网雷达的协同干扰前，先对单架无人机运动模型进行分析。

设雷达的坐标为(xa，ya，za)，无人机个数为k，j表示假目标与无人机，rj表示j到达雷达的径向距离。θj表示仰视角，σj表示方位角，βj为航向角，hj表示飞行高度，当j=q时所有符号表示假目标的相关参数，j=di时表示第i架无人机的相关参数。直角坐标系下无人机定高飞行的运动关系如图2所示[5]。

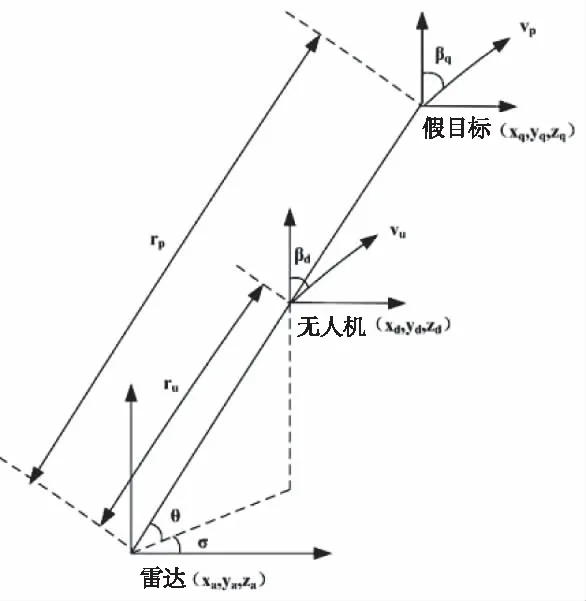
图2 无人机做定高运动时的运动关系

无人机做定高飞行的运动模型为

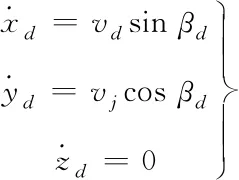
(1)

根据球坐标系和直角坐标系的转换关系，将无人机的运动模型转换为球坐标系，已知

(2)

对式(2)进行求导变换，可得无人机在球坐标系下的运动模型

(3)

由(1)、(3)可得无人机的运动参数为：

(4)

3.2.2 蚁群算法求解

1)蚁群算法求解最优路径的基本思想

蚁群算法是一种模拟蚂蚁觅食行为的模拟优化算法，主要用于解决路径规划等离散优化问题。其中，蚁群活动、信息素发挥和信息素增强三部分构成了算法的核心，本文用到的蚂蚁释放信息素模型为ACS 模型

(5)

Lk表示第k个无人机所构造的路径的总长度，Q为常数，表示蚂蚁循环一次释放的信息素的总量。

为了避免算法中无人机过快地向局部最优区域集中，当所有无人机完成一次循环后，各个点间连接途径上的信息浓度应进行如下更新：(ρ表示信息素的挥发程度，Δτij表示所有无人机在点i与点j连接途径上遗留下的信息浓度总和)

(6)

本文中该算法应用的具体流程为：

Step1：参数初始化。

(7)

其中ηij为边弧(i，j)的能见度或称局部启发因子，allowedk(k=1，2，……，m)为未选定的点的集合。α表示信息启发因子，它的值越大，蚂蚁选择路径的随机性则越弱，就会根据以往的记忆，选择之前走过的路径；β为期望启发因子，它的值越大，蚁群就越容易选择在特定范围内最短的路径。

Step3：确定最大迭代次数n，放m只蚂蚁到定高平面中的无人机坐标点上。

Step4：将每只蚂蚁选择的初始坐标点和其按照信息素含量转移得到的下一个坐标点放入当前解集中……经过n个时刻，蚂蚁g便可以完成该平面内所有坐标点的遍历，形成一个完整的回路。

Step5：更新信息素。

Step6：迭代次数小于最大迭代次数，则返回第4步进行循环，否则输出最短路径，程序停止。

本文假设无人机做水平方向的直线运动，不存在爬升或俯冲，则无人机对组网雷达进行协同干扰时形成的航迹路线都是从起点开始，完成任务再飞回起点的过程。因此该航迹规划问题可转化为TSP问题，可利用蚁群算法对其求解。

其目标函数为

(8)

2)蚁群算法应用求解

求无人机坐标。过(xa，ya，za)和(xq，yq，zq)两点间的直线与平面z=hdi的交点即无人机在对应时刻的坐标

(9)

计算多无人机之间的距离矩阵A=(dij)v×v，在无人机飞行高度范围内依次取一定高度hdi，运用蚁群算法进行计算，选取出使路径最优的平面zdi=hdi。

3.2.3 无人机数量优化

一次筛选分析。根据无人机速度范围计算一个时间间隔内的距离范围，距离矩阵A中两坐标间隔在该距离范围以内的视为同一无人机运动得到，由此减少无人机数量，进行第一次筛选；

聚类法的应用。利用聚类法将剩余所有无人机对应时刻坐标画为生成树，并求得各类中点的坐标，以此方便确定无人机数量的个数及无人机轨迹。

二次筛选分析。由图(2)的几何关系可得

(10)

结果验证。再次进行一次距离矩阵的求解，验证两两无人机之间的距离dij是否大于ΔS。

4 案例

现本文建立以下实例来应用该模型进行求解仿真。

某组网雷达系统由5部雷达组成，雷达最大作用距离均为150km，5部雷达的地理位置坐标分别为雷达1(80，0，0)，雷达2(30，60，0)，雷达3(55，110，0)，雷达4(105，110，0)，雷达5(130，60，0)(单位：统一为km)。已知20个连续的经融合中心确认的航迹点形成的合理航迹，将被组网雷达系统视为一条真实的目标航迹。

无人机的飞行速度控制在120km/h-180km/h，飞行高度控制在2000m-2500m。无人机间距需控制在100 m以上。所产生的20个目标虚假航迹点坐标如图3，时间间隔为10秒。

图3 20个虚假航迹点坐标图

图4为假目标和雷达的可视化位置图。接下来应用以上模型对该问题进行求解。

图4 假目标和雷达的Matlab视图

首先应用蚁群算法求出最优路径的水平高度，图5为蚁群算法的最短路径图，图中蓝色的圆圈为初始产生的无人机的坐标，共有100个，红色的连线为蚁群算法计算的最优路径，图6为蚁群算法的最短距离图。经过蚁群算法对多个平面高度上产生的无人机位置进行遍历，得到最优的水平高度为2325米。

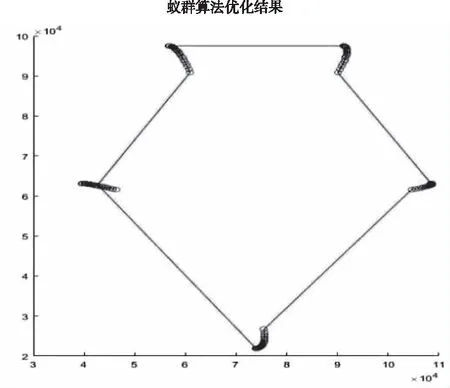
图5 蚁群算法的最短路径图

图6 蚁群算法的最短距离图

其次，根据一次筛选，得到无人机数量减少到33个。

然后，对所有无人机坐标点进行聚类分析，并对各个点集进行排列，分别求出各条曲线附近无人机的偏移角度进行第二次筛选，如图7所示，共得到五条曲线。将偏移角度在误差范围Δ=0.5°以内的的所有角视为同一个角，由同一个无人机运动得到，最后得到结果为21架无人机。

图7 无人机的偏移角度

最后对无人机两两之间距离进行验算得，该21架无人机均符合给定距离条件，因此认为21架为求得的的最少无人机数量，并可得出这21架无人机各时刻的坐标即其调度策略，部分数据结果如图8。

图8 21架无人机在各时刻的位置(部分数据)

5 结束语

文中所提出的基于蚁群算法和聚类法的多无人机对组网雷达协同干扰中的优化模型，可以得到在实现既定假目标干扰任务的前提下无人机的最优调度策略，解决了目标问题，对利用无人机对组网雷达进行协同干扰具有实际指导意义。但本文对无人机的运动状态有一定的限制因素，通过Matlab编程虽然实现了该模型，找到了问题的最优解，但随着参数的调节运行结果有一定的随机性，在之后的研究中可以对此进行扩展。