基于Prophet融合MGF提取的网络流量预测

朱 江，潘成胜，孔志翔，石怀峰，

(1. 南京信息工程大学电子与信息工程学院，江苏 南京210044；2. 南京理工大学自动化学院，江苏 南京210094)

1 引言

网络流量预测是网络管理和规划的重要依据。准确的流量预测能够帮助管理者提前制定网络资源分配策略，有效解决即将到来的拥塞事件[1][2]。因此，建立准确的流量预测模型具有重要的实际意义。

现有网络流量的预测方法可总结为两类：适用于线性系统预测的统计方法和非线性预测系统的机器学习方法。典型的时间序列预测模型有自回归滑动平均(ARMA)和以它为基础组合改进的模型。例如：Guo等[3]提出利用乘性季节ARIMA模型进行移动通信流量预测。但是，网络的发展导致网络流量的复杂性及突发性愈发加强，传统的泊松分布、高斯分布等线性模型已不能满足现代网络流量的特点[4]。随着人工智能的发展，出现了基于机器学习算法的支持向量回归(SVR)[5]、极限学习机(ELM)[6]、人工神经网络(ANN)等非线性模型。前两个方法虽预测效果不错，但SVR模型的好坏太依赖于核函数的选取，ELM模型训练精度的提高完全依赖于隐藏层节点数的增加、且模型稳定性差。Nipun等[7]提出利用LSTM预测网络流量，LSTM有一定解决RNN(循环神经网络)长期依赖的能力。但随着时间序列的过长，输入信息的变多，单一的LSTM模型训练难以收敛至全局最优，于是Li[8]等提出CNN融合LSTM的模型进行预测。CNN能将时间序列的高维特征提取出来，LSTM再对所提取的高维特征进行流量的预测。但是，对时间序列的特征而言，不是每个特征的重要程度都一样，网络流量突变点附近的特征可能比平稳区域的特征更加重要[9]。针对不同时序特征的重要度不同，有专家提出利用注意力机制(Attention)[10]解决此类问题。注意力机制在机器翻译、图像生成描述等领域具有很好的效果[11]，对于感兴趣的部分往往会分配大量的注意力，获得更大的权重，从而达到优化模型的效果。

由于网络流量在不同的时间尺度下具有长相关、混沌等特性[12-14]，传统的网络流量预测模型无法有效提取流量的这种多分形特性，因此需要将不同特性的流量分量从数据中分离出来再分别进行预测。利用Prophet模型可将时间序列分解为多层的能力，本文提出一种基于Prophet融合粗细粒度特征提取的神经网络流量预测模型，利用Prophet模型将流量序列分解成非线性项及附加项两个分量。由于Prophet模型相较于LSTM而言对时间序列的季节性、假期性更为敏感，擅长处理具有大异常值和趋势变化的日常周期数据[15][16]。所以对附加项建立Prophet模型，对非线性项建立CNN和基于Attention的LSTM模型进行预测。其中，CNN提取序列显著细粒度特征，基于Attention的LSTM对特征的维度使用Attention(Dimensions Attention)提取序列粗粒度特征，从而实现粗细粒度特征提取的融合，并给重要的特征分配更多的权重以提高其对结果的影响。最后将两各模型预测出的结果进行相加得到网络流量的预测值。

2 Prophet融合多粒度特征提取的网络流量预测模型

基于Prophet模型，本文提出一种融合多粒度特征提取的神经网络PFMGNet(Prophet Fusion of Multi-grained Network)预测模型，其模型框架如图1所示。

模型共由四部分组成，详细介绍如下：

1)首先采用Prophet模型的可分解方法，将网络流量历史数据y(t)分解成趋势项g(t)，随机项ε(t)，季节项s(t)和节假日h(t)，在本文中，前两项称为非线性项A(t)，后两项称为附加项D(t)。

2) 将附加项D(t)通过Prophet模型预测得到t+i这段时间内的预测值D(t+i)，其中i=1，2，…，N。

3) 将非线性项A(t)通过PFMGNet模型预测得到预测值A(t+i)，其中i=1，2，…，N。CNN能够提取序列的细粒度特征，基于Attention的LSTM提取隐藏在细粒度特征中的粗粒度特征，同时能够有效避免因步长过长造成长期依赖的问题。

4) 将2)、3)中的结果相加得到最终的网络流量预测结果：

y(t+i)=D(t+i)+A(t+i)i=1，2，…，N

2.1 Prophet模型

Prophet是一种新型的预测模型，擅长处理具有大异常值和趋势变化的日常周期数据，其拟合程序运行速度极快。Prophet模型总体运行过程如图2所示，通过建模与评估模型两个模块的循环迭代最终优化出结果。

Prophet模型可将序列分解成三个函数，其中ε(t)为随机项。

y(t)=g(t)+s(t)+h(t)+ε(t)

(1)

式(1)中g(t)为趋势项，用来表示时间序列的非线性性趋势，函数表达式如式(2)所示

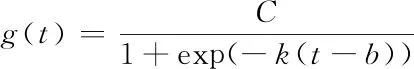
(2)

其中，C表示模型容量，k、b分别表示增长率和偏移量，随着t的增长模型趋向于C。

式(1)中s(t)为季节项，用来表示时间序列的周期性变化(例如日季节性、周季节性)，函数表达式如式(3)所示

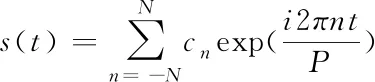
(3)

其中，P为目标序列的周期，cn为要估计的系数参数，服从cn～Normal(0，σ)分布。

式(1)中h(t)为假期项，表示假期等特殊因素对时间序列造成的影响，函数表达式如式(4)所示

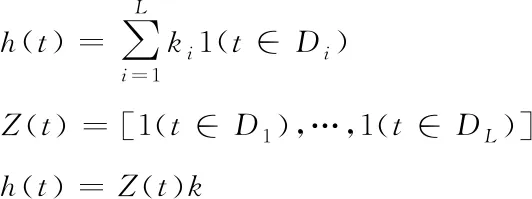
(4)

其中，Di表示假期i对应的日期，Z(t)表示时间t是否是假期，是为1，不是为0。参数k服从k～Normal(0，v)，v越小则模型适应波动的能力越小，反之越大。

2.2 1D-CNN

1D-CNN是用于处理序列数据的一种特殊神经网络。与2D-CNN不同的是，1D-CNN的卷积核只需朝着一个维度滑动进行卷积。卷积层可以通过训练得到满足损失函数最小的一组最优卷积核，利用卷积核实现自动特征提取。池化层能有效减少模型参数，提高神经网络的训练速度，并且可以防止模型过拟合，因此在此部分不使用丢弃算法(Dropout)。卷积层与池化层的堆叠形成深度网络结构，逐层提取高维序列的特征。

2.3 基于注意力机制的LSTM

为了解决梯度下降和梯度爆炸的问题，LSTM模型在循环神经网络(RNN)中对循环层进行改进，使用输入门、遗忘门和输出门来控制记忆过程。这是一种特殊的时间递归网络模型，适合处理和预测时间序列[17]。由于网络流量是时间序列且序列之间的信息是相互关联的，因此选用LSTM模型学习序列的上下文信息。

注意力机制(Attention)通俗而言就是对模型感兴趣的部分分配更多的权重。在时间序列的预测问题上，不是每个特征的重要程度都一样，网络流量突变点附近的特征可能比平稳区域的特征更加重要。Attention的任务是对于LSTM网络得到隐层输出序列a(t)，根据权重分配计算不同特征向量对应的概率，不断更新迭代出较优的权重参数矩阵α(t)，将其与特征向量a(t)加权求和后作为Attention的输出，最后通过全连接层计算出预测的结果。基于注意力机制的LSTM网络结构如图3所示。其中，x(t)表示输入序列，a(t)表示学习得到的输入序列x(t)的特征，α(t)表示各特征的注意力权重，y(t)表示输出结果。

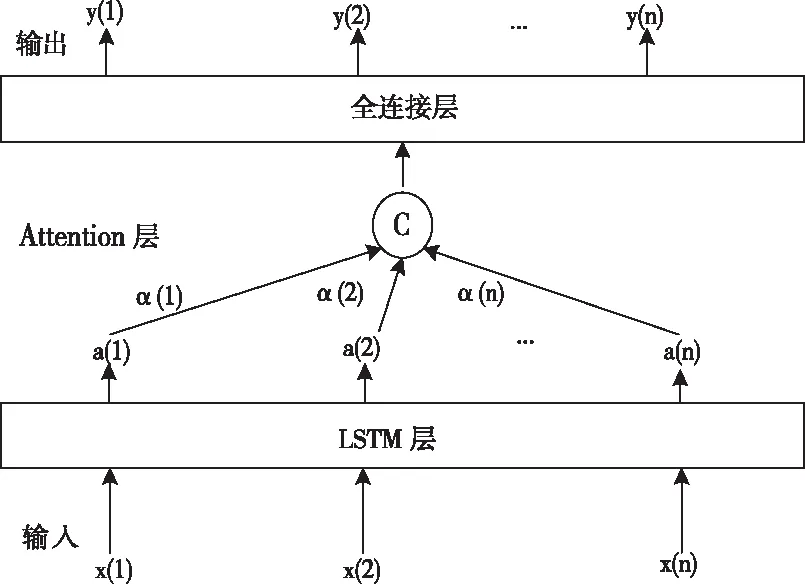
图3 基于Attention的LSTM网络结构

其中Attention层的权重为

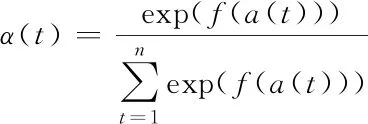
(5)

其中f(a(t))是评价函数，可表达为f(a(t))=WTa(t)，W为训练参数，对Attention层权重求和得到最后的特征向量

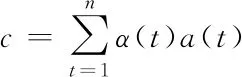
(6)

2.4 参数化计算过程

经Prophet模型分解后的A(t)分量作为输入序列，本文采用单步预测[18]，同时引入滑动窗口T，其原理为：通过一系列历史流量数据(A(t)，A(t+1)，A(t+2)，…，A(t+T-1))来预测未来A(t+T)时刻的流量。模型计算过程如下：

1)卷积部分包含两个1DCNN和最大池化层，卷积层的卷积核尺寸均为2，1DCNN_1、1DCNN_2的过滤器的个数分别为256和128，1D最大池化层的核尺寸也为2。

2)将数据利用flatten展平，并重复向量4次以进一步填充LSTM层。在LSTM层加入了丢弃算法(Dropout)以防止模型的过拟合，在经过LSTM层后使用全连接层得到注意力权重，对特征赋予权值。这里，LSTM层的输出单元大小设置为128。

3)在LSTM后加入一个带激活函数(Relu)的全连接层，最后再加入一个输出节点给出预测结果实现单步预测。

3 仿真研究

3.1 实验数据

为了验证模型的有效性，本文选取一个开放的数据集MAWILab中骨干网一条链路的流量作为实验数据。采集2020年5月1日0点至2020年5月30日23点，周期为1h的平均网络流量，共720组数据。其中前576组作训练集，初次训练选取训练集中10%的数据作为验证集，保存好最佳模型后继续用完整的训练集进行训练，后144组作测试集。

预测前先对样本数据进行归一化操作，其目的在于消除指标之间的量纲影响，使后面结果分析中的指标处于同一数量。同时，当样本数值差异太大时，容易造成神经网络训练收敛速度变慢。在本文中，利用Python中的MinMaxScaler函数将数据规范在(-1，1)区间，输出结果前再进行反归一化操作。t时刻A(t)归一化的结果为A′(t)

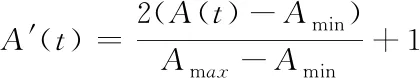
(7)

其中，Amax，Amin分别为流量数据的最大值和最小值。

3.2 实验参数和评价指标

本研究试验环境为：Python3.7编程环境，网络框架使用Keras搭建；操作系统为Windows10 64bit，处理器为Intel(R) Core(TM) i7-9700CPU @ 3.00GHz，内存为32GB。

在本次实验中，滑动窗口T的大小设置为4，即通过4个历史网络流量数据(A(t)，A(t+1)，A(t+2)，A(t+3))来预测未来A(t+4)时刻的流量。优化器选用Adam，学习率设置为0.0001，模型训练的迭代次数epoch为100，dropout设为0.5。

本文选取了两种评价指标作为评判模型效果好坏的指标，具体如下：

1)平均绝对百分比误差(MAPE)，MAPE之所以可以描述准确度是因为MAPE本身常用于衡量预测准确性的统计指标，如时间序列的预测。MAPE的取值范围为[0，+∞)，越接近于0说明模型越好。具体公式如下

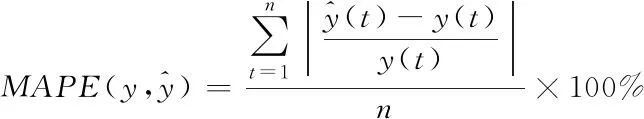
(8)

2)确定性相关系数(R2score)，R2的取值反应模型的优异程度。R2的范围为[0，1]，与MAPE相反，R2的值越接近于1说明模型越好，反之越差。具体公式如下

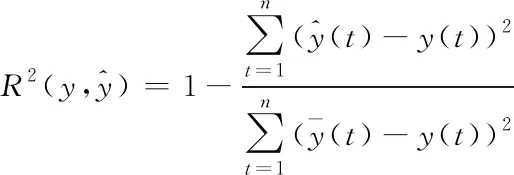
(9)

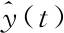
3.3 实验结果及分析

3.3.1 Prophet模型分解

利用Prophet模型将流量数据分解，成分分析如图4所示。模型将序列解成四个部分：趋势g(t)，节假日h(t)，周季节性和日季节性，其中，周季节性与日季节性叠加形成季节项s(t)。

由图4(a)可以看出网络流量在5月8日达到峰值后开始下降，自5月14日起缓慢上升。图4(c)中显示双休的流量值低于周一至周五的流量值，考虑到这种情况主要因为周一至周五是工作日造成，周六周日人们休息，使用网络的时间减少导致网络流量值低。图4(d)中显示了一天中的流量分布，可以看出白天的流量值普遍高于夜晚的流量值，在凌晨4点至5点间达到一天的最低值，下午3点左右到达最高，这种网络流量使用情况的谷值与峰值分布符合实际情况，说明了所选数据的可靠性。

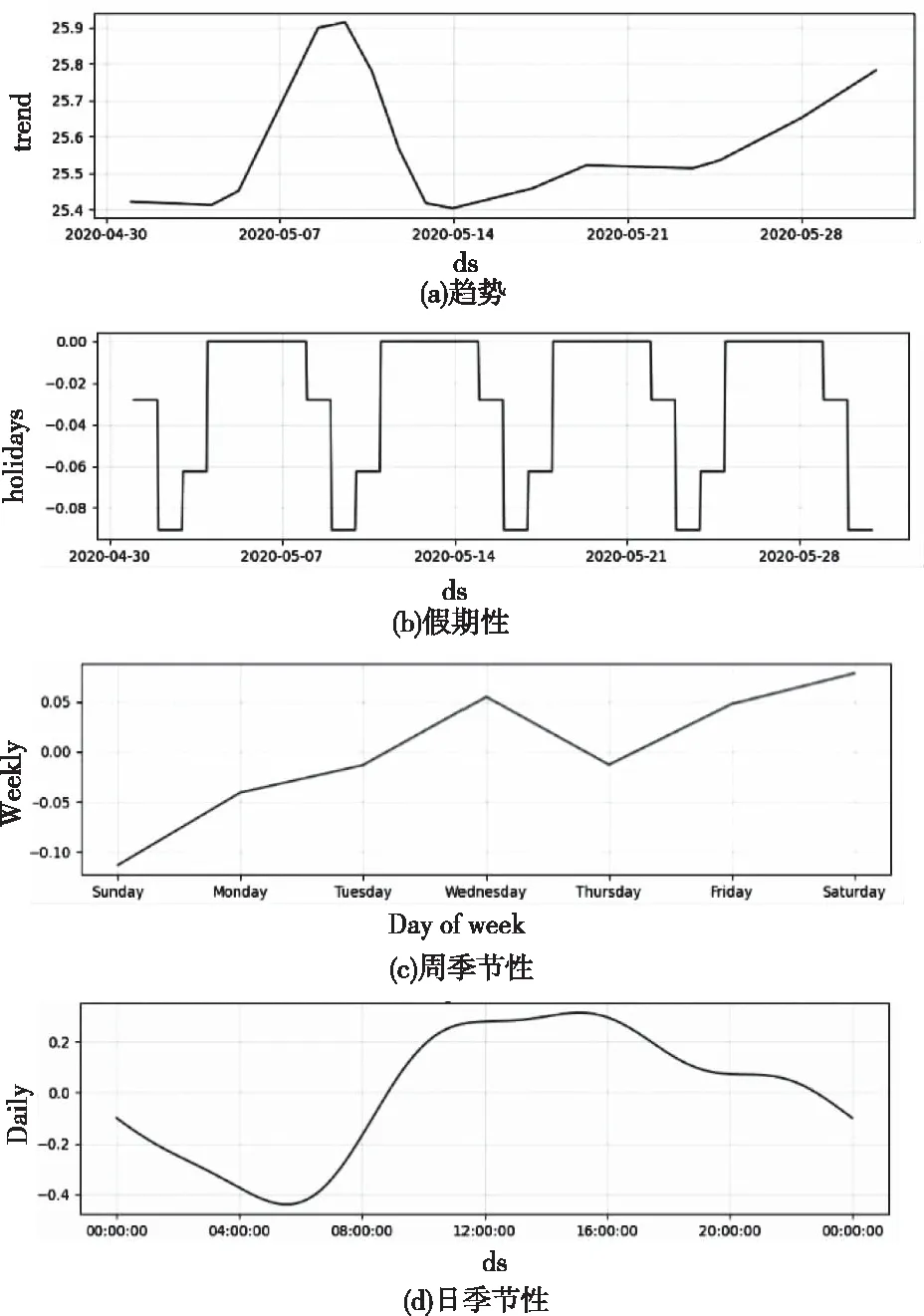
图4 网络流量成分分析图

3.3.2 不同模型对比

为了验证本文所提模型的优越性，选取模型与其它模型分别从预测精度和时耗两方面进行对比分析，表1为其对比结果。

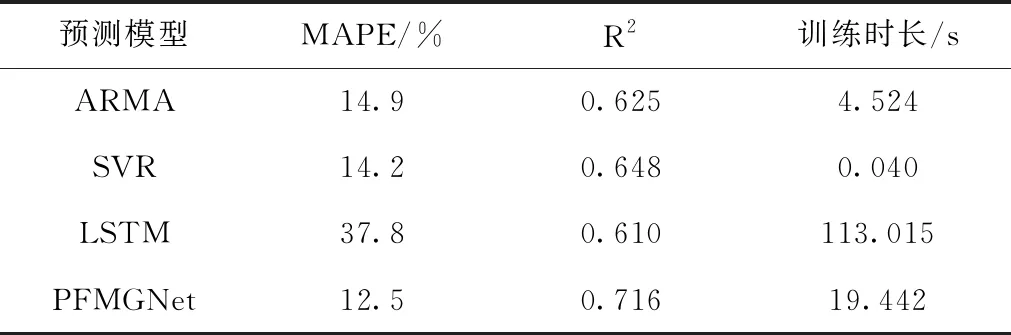
表1 不同模型评价指标结果

各模型分别训练5次后取平均值作为最终结果，分析表1可知：

1) LSTM模型尽管具备一定的长序列特征挖掘能力，但随着输入的变长，序列所包含的信息变多，单一的LSTM模型训练难以收敛至全局最优，造成预测效果变差。虽然R2值与其它模型相差不多，但MAPE较其它模型而言结果很差。另外LSTM模型由于不能并行计算，训练耗时极长，与传统预测模型相差几个量级。

2)ARMA模型在R2指标上表现也不佳，对网络流量序列进行统计分析，其结果如表2所示。由表2可以看出原始数据全部样本的偏度为0.7469，峰度为0.0629，这表明数据呈右尾分布，且不符从正态分布。根据ADF检验来看，由于假设检验值-2.6678大于5%的置信度(-2.8657<-2.6678<-2.5690)，说明只有90%的把握认为原假设不存在单位根，因此判定原始流量数据是非平稳的，不适合ARMA这类线性系统预测模型。

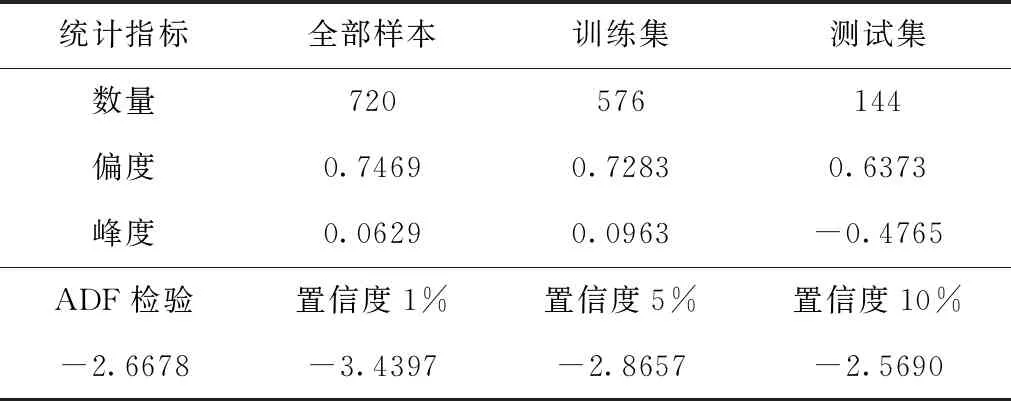
表2 网络流量数据统计分析

3)SVR采用多项式(POLY)核函数。由于SVR的数据量少，因此它的训练时长也是最快的，且预测效果优于传统方法的线性预测模型。

4) 本文所采用的PFMGNet模型，较其它模型效果显著，MAPE指标比LSTM模型减少了25.3%、R2指标比LSTM模型提高了0.106。训练时耗虽比不上传统模型，但较其它神经网络模型也有较大的缩短。

3.3.3 消融实验

为验证模型的有效性，选取同一组原始流量数据。分解设置CNN+LSTM和CNN+基于注意力的LSTM进行消融实验，图5和表3为消融实验的结果。

表3 消融实验模型评价指标结果

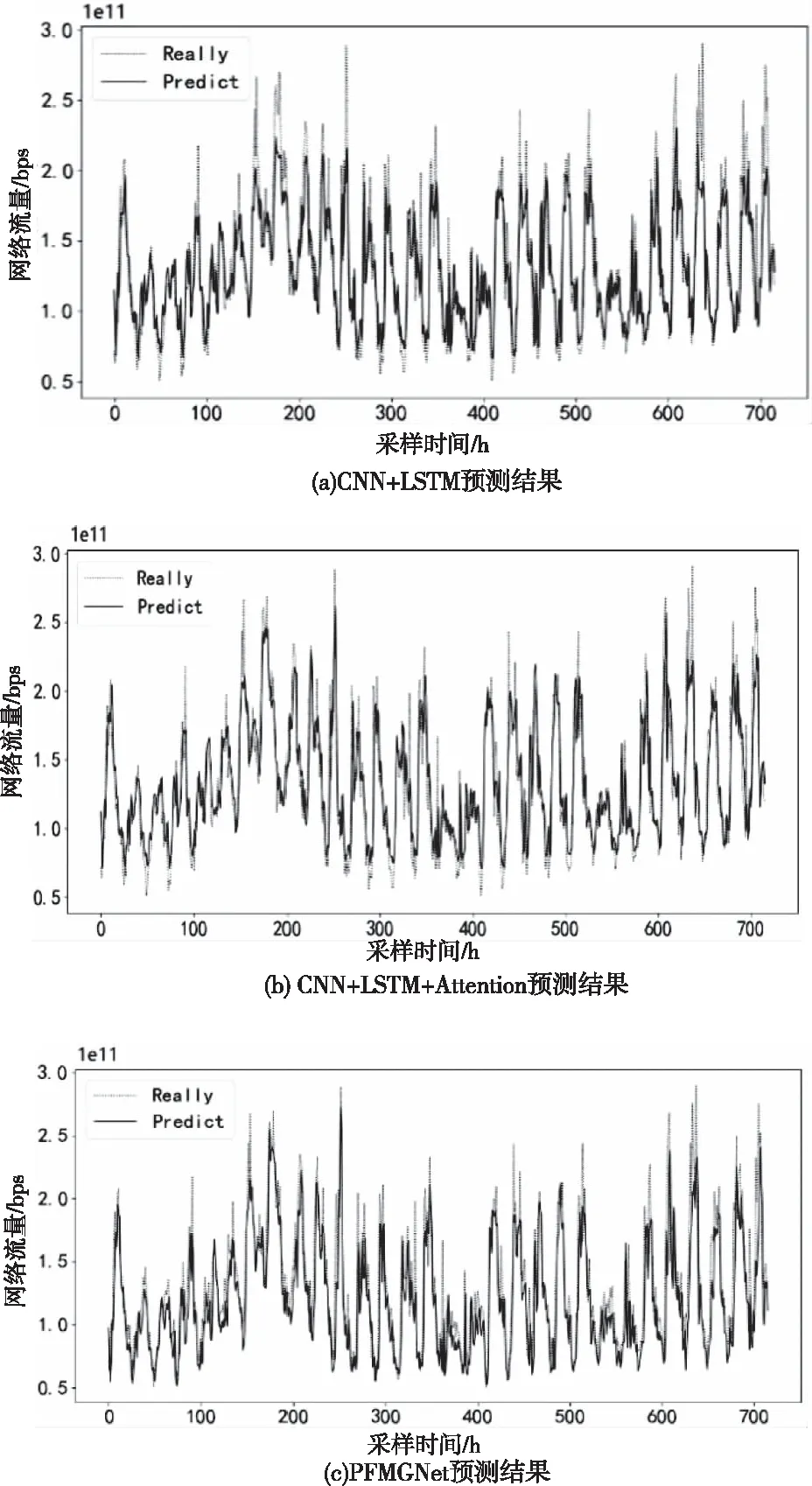
图5 消融实验模型预测结果图

可以看出：

1)CNN+LSTM模型虽融合了两种模型的特点，但对于一些异局部特征附近预测效果很差，且在部分时间段的预测出现了一定的滞后现象。

2)CNN+LSTM+Attention模型由于注意力机制的效果，使模型的特征提取更注重于显著特征的提取上，根据图5(b)可看出模型对突变点的预测更加准确(例如图5(b)中时间点250、580附近的峰值)，相较于1)模型一定程度上减少了显著特征的丢失。

3)根据表1、表3可以看出本文提出的PFMGNet模型在各项精度指标上为最优，且时耗也比其它神经网络快。通过图5(c)可看出，PFMGNet模型综合了2)中模型优点的同时也优化了对序列局部特征的提取，对于实际网络流量的变化趋势的预测基本一致。说明模型对于时间序列的季节性分量、节假日因素有着很好的预测效果。另一方面，图6显示了Attention作用于特征维度的权重分配，从图6中可以看出第23维的权重明显大，为0.214。

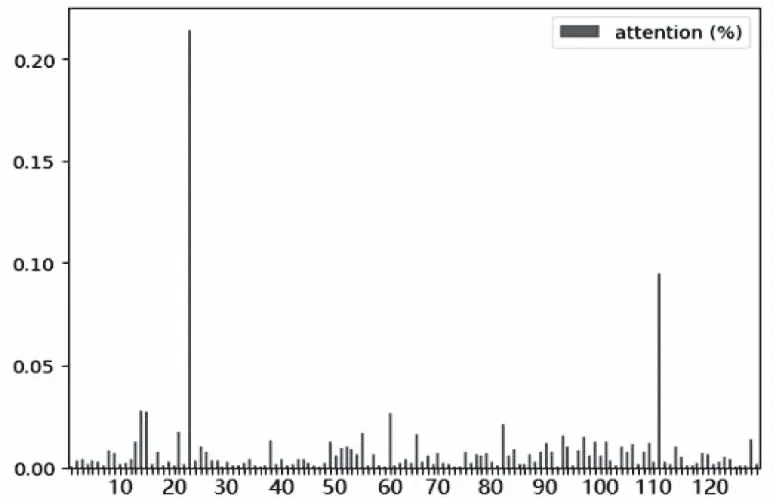
图6 注意力机制的权重汇总图

4 小结

通过实验可以看出，单一的模型不能很好的预测网络流量，更好的方式是根据网络流量的特性通过模型的分解、组合后再进行预测。同时结果表明，本文提出的基于Prophet融合多粒度特征提取的模型对于网络流量的预测具有更好的效果，MAPE评价指标为12.5%，R2分数达到0.716；相较于传统的LSTM模型，MAPE和R2效果分别优化了25.3%、0.106。当然本模型也有需要改进的地方，比如对于多条链路中网络流量该如何预测，有待进一步研究。