消防安全告知承诺管理中的核查策略博弈分析
2021-11-17王冠鹏孙洛浦
王冠鹏 孙洛浦
(大庆市消防救援支队,黑龙江 大庆 163000)
0 引言
2019年5月,中办、国办联合印发《关于深化消防执法改革的意见》(以下简称《意见》),《意见》中明确提出“简化公众聚集场所投入使用、营业前消防安全检查,实行告知承诺管理”。2021年4月,《消防法》新修订内容提出“公众聚集场所投入使用、营业前消防安全检查实行告知承诺管理”“消防救援机构对申请人提交的材料进行审查”“消防救援机构应当根据消防技术标准和管理规定,及时对做出承诺的公众聚集场所进行核查”。告知承诺管理主要是指公共场所依据消防安全标准向消防监管部门做出消防安全承诺后,消防监管部门对场所实施现场核查和例行检查的消防监管手段,是推动“放管服”改革和优化营商环境的有效举措。然而,随着简化审批流程、加强事中事后监管等一系列举措的出台,消防监管部门与社会单位间在消防监管过程中的关系和角色出现了微妙的变化。作为消防安全监管的创新举措,关于消防告知承诺管理的相关研究尚未形成完整的理论体系。即便已有研究给予消防安全告知承诺管理一定的关注,但其成果多是围绕现状梳理、问题分析、经验总结等内容展开,缺乏从理论视角出发的消防告知承诺管理研究内容。
近年来,演化博弈理论已在政府监管与治理等相关问题中有一定应用,安全监管、环境监管、食品监管是政府与社会组织博弈研究的重点议题。为此,本研究将引入演化博弈理论,探讨消防监管部门与公共场所管理部门在消防告知承诺管理中的策略博弈关系。本研究将构建告知承诺管理背景下消防监管部门与公共场所管理部门的现场核查博弈模型,并进一步分析双方策略选择的博弈和行为交互的过程,以期能够为告知承诺管理的实施和消防执法改革工作的推进提供理论指导与实践参考。
1 消防告知承诺中的现场核查博弈模型构建
1.1 基本假设与参数说明
结合有关消防执法改革的文件内容和相关文献成果,为构建告知承诺管理背景下消防监管部门与公共场所管理部门的现场核查博弈模型和支付矩阵,现提出如下基本假设:
假设1:消防监管部门和公共场所管理部门在现场核查博弈模型中均是有限理性的,双方在博弈过程中的策略选择是随机且独立的。
假设2:消防监管部门在博弈过程中的策略集为{严格核查、不严格核查},其中,选择严格核查策略的概率为x
(0≤x
≤1);不严格核查策略的概率为1-x
。公共场所管理部门在博弈过程中的策略集为{如实承诺、失实承诺},其中,选择如实承诺策略的概率为y
(0≤y
≤1);失实承诺的概率为1-y
。假设3:当消防监管部门选择严格核查策略时,就会发现公共场所管理部门未履行的消防安全承诺事项。
C
为消防监管部门制定公共场所消防安全标准、审核告知承诺管理中的组织成本,C
>0;C
为消防监管部门在公共场所管理部门做出消防安全承诺后,进行现场核查和例行检查时的监管成本,C
>0;G
为公共场所在日常经营中,所获得的相关收益,G
>0;C
为公共场所管理部门按照消防监管部门制定的公众聚集场所消防安全标准,对标实施消防安全管理和采买消防设施的投入成本,C
>0;F
为公共场所管理部门因未履行消防安全承诺,被消防监管部门责令停止使用、暂停营业、临时查封期间所受到的经营损失,F
>0;F
为公共场所管理部门因未履行消防安全承诺,受到消防监管部门的行政处罚所受到的罚款损失,F
>0;F
为公共场所管理部门在消防监管部门现场核查时,因场所实际与消防安全承诺事项不匹配时,被消防监管部门依法记入信用记录而受到的额外损失(社会声誉损失、经营损失),F
>0;R
为消防监管部门在现场核查中,因作出撤销审批、责令停止使用、行政处罚及公开相关事项等执法行为而获得的社会声誉收益,R
>0;L
为消防监管部门因未履行现场核查职责时,因发生火灾事故或其他安全事故,上级消防监管部门对其进行的处罚,L
>0。α
为消防监管部门在公共场所管理部门进行承诺后,进行现场核查和例行检查时的核查力度,0≤α
<1,α
越小表示消防监管部门核查越不严格,在支付水平上表现为核查成本、行政处罚力度的下降。θ
为公共场所管理部门按照消防安全标准如实承诺的程度,0≤θ
<1,θ
越小代表公共场所管理部门如实承诺水平越低,在支付水平上表现为场所消防投入成本的降低和场所因未如实承诺而造成的收益损失增大。在此基础上,给出消防监管部门与公共场所管理部门间策略的支付矩阵,见表1。
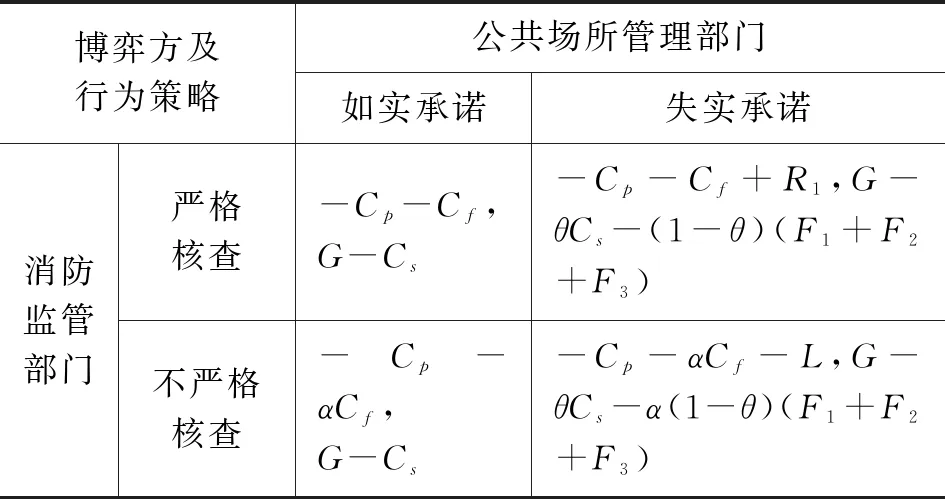
表1 消防监管部门与公共场所管理部门的博弈支付矩阵
1.2 演化博弈系统均衡点求解
根据支付矩阵,消防监管部门选择严格核查策略的适应度为:
U
=y
(-C
-C
)+(1-y
)(-C
-C
+R
)(1)
消防监管部门选择不严格核查的适应度为:
U
=y
(-C
-αC
)+(1-y
)(-C
-αC
-L
)(2)
消防监管部门博弈策略的平均适应度为:

(3)
同理,公共场所管理部门选择如实承诺策略的适应度为:
U
=x
(G
-C
)+(1-x
)(G
-C
)(4)
公共场所管理部门选择失实承诺的适应度为:
U
=x
[G
-θC
-(1-θ
)(F
+F
+F
)]+(1-x
)[G
-θC
-α
(1-θ
)(F
+F
+F
)](5)
公共场所管理部门博弈策略的平均适应度为:

(6)
根据Malthusian方程,消防监管部门选择严格核查策略的数量增长率为:
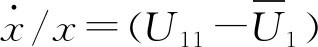
(7)
公共场所管理部门选择如实承诺策略的数量增长率为:
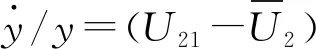
(8)
据此,得到消防监管部门与公共场所管理部门的复制动态方程为:

x
(1-x
)[-(1-α
)C
+R
+L
-(R
+L
)y
](9)
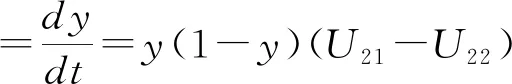
y
(1-y
)(1-θ
)[-C
+α
(F
+F
+F
)+(1-α
)(F
+F
+F
)x
](10)

2 消防告知承诺中的现场核查博弈系统稳定性分析及数值仿真
2.1 统演化方向分析
系统初始状态的位置将会影响系统的演化趋势,当x
>x
时,G
(y
)>0、G
(1)<0、G
(0)>0,得出y
=1是该模式下的稳定状态;当x
<x
时,G
(y
)<0,G
(1)>0,G
(0)<0,此时y
=0是系统的稳定状态。同理,当y
>y
时,F
(x
)<0,F
(1)>0,F
(0)<0,此时x
=0是系统的稳定状态;当y
<y
时,F
(x
)>0、F
(1)<0、F
(0)>0,此时x
=1是系统的稳定状态。综上,得到了系统的演化相位图,如图1。
图1 博弈系统的演化相位图
2.2 雅克比矩阵求解
在对系统复制动态方程进行演化分析的基础上,研究将利用雅克比(Jacobian)矩阵对复制动态系统均衡点的局部渐进稳定性进行分析,并进而对演化稳定策略进行识别。该系统的雅克比矩阵为:

(11)
其中:a
=(1-2x
)[-(1-α
)C
+R
+L
-(R
+L
)y
];a
=-x
(1-x
)(R
+L
);a
=y
(1-y
)(1-θ
)(1-α
)(F
+F
+F
);a
=(1-2y
)(1-θ
)[-C
+α
(F
+F
+F
)+x
(1-α
)(F
+F
+F
)]。矩阵J
的行列式detJ
为:detJ
=a
a
-a
a
,矩阵J
的迹trJ
为:trJ
=a
+a
。同时,将均衡点取值带入矩阵,得到的矩阵行列式detJ
和迹trJ
的表达式,见表2。
表2 复制动态系统均衡点对应的矩阵行列式和迹表达式
2.3 数值仿真分析
根据Friedman提出的方法,在雅克比(Jacobian)矩阵中,只有当均衡点的矩阵J
满足行列式detJ
>0,迹trJ
<0时,均衡点才是博弈系统的演化稳定策略。研究通过分析不同条件下,均衡点O
(0,0)、A
(1,0)、B
(1,1)、C
(0,1)以及D
(x
,y
)的行列式与迹的取值,认为消防监管部门与公共场所管理部门的博弈系统中,存在“不严格核查、失实承诺”、震荡无稳定策略、“严格核查、失实承诺”以及“不严格核查、如实承诺”共4类情形。同时,将利用Matlab 2018a软件对策略演化过程进行模拟仿真。得到的系统仿真结果为博弈主体策略分别为0.2、0.5、0.8时的系统演化轨迹。(1)情形1。当-C
+α
(F
+F
+F
)<0,-(1-α
)C
+R
+L
<0时,消防监管部门选择严格核查策略的相对净支付恒负,且公共场所管理部门选择如实承诺与失实承诺的净收益之差小于0,点O
(0,0)为系统的演化稳定策略。假设α
=0.
8,θ
=0.
5,C
=50,C
=100,F
=20,F
=20,F
=20,R
=5,L
=10,代入复制动态系统,得到仿真结果,如图2。随着消防监管部门与公共场所管理部门策略博弈的演化时间增加,消防监管部门选择严格核查策略与公共场所管理部门选择如实承诺策略的概率同时减小,最终形成了“不严格核查、失实承诺”的策略组合。
图2 情形1下的博弈仿真结果
(2)情形2。当-C
+α
(F
+F
+F
)<0,-C
+F
+F
+F
>0,-(1-α
)C
+R
+L
>0时,点O
(0,0)、A
(1,0)、B
(1,1)、C
(0,1)是该系统中鞍点和不稳定点,该情形下不存在稳定的演化策略。假设α
=0.8,θ
=0.5,C
=50,C
=100,F
=20,F
=20,F
=20,R
=10,L
=20,代入复制动态系统,得到仿真结果,如图3。随着双方策略博弈的演化时间增加,消防监管部门的策略选择与公共场所管理部门的策略选择呈现出周期性往复的波动特征,未能形成稳定的策略组合,而是形成一种策略循环的演化路径。此时,消防监管部门严格核查策略与不严格核查策略,公共场所管理部门如实承诺策略与失实承诺策略是相互转化的。
图3 情形2下的博弈仿真结果
(3)情形3。当-C
+F
+F
+F
<0,-(1-α
)C
+R
+L
>0时,消防监管部门选择严格核查策略的相对净支付始终为正值,为维持公共场所管理部门消防安全管理水平消防监管部门将选择严格核查策略。同时,公共场所管理部门选择如实承诺的净收益减去失实承诺的净收益恒负,点A
(1,0)为系统的策略稳定点。假设α
=0.8,θ
=0.5,C
=50,C
=100,F
=20,F
=10,F
=10,R
=10,L
=20,代入复制动态系统,得到仿真结果,如图4。随着双方策略博弈的演化时间增加,消防监管部门选择严格核查策略逐渐增大,公共场所管理部门选择选择如实承诺策略的概率随之减小,形成了“严格核查、失实承诺”的策略组合。
图4 情形3下的博弈仿真结果
(4)情形4。当-C
+α
(F
+F
+F
)>0时,消防监管部门选择严格核查策略的相对净支付恒负。同时,公共场所管理部门选择如实承诺的净收益减去失实承诺的净收益为正值,如实承诺策略成为公共场所管理部门博弈策略的自律选择,点C
(0,1)为系统的策略稳定点。假设α
=0.8,θ
=0.5,C
=50,C
=100,F
=40,F
=20,F
=20,R
=10,L
=20,代入复制动态系统,得到仿真结果,如图5。随着双方策略博弈的演化时间增加,消防监管部门选择严格核查策略的概率逐渐减小,公共场所管理部门选择如实承诺策略的概率逐渐增大,得到了“不严格核查、如实承诺”的策略组合。
图5 情形4下的博弈仿真结果
3 结论
对公共场所实施告知承诺管理是《关于深化消防执法改革的意见》中提出的重要监管模式创新,是破除消防监管门槛和限制、推动简化审批和强化监管衔接、加强事中事后监管的重要举措。本文运用演化博弈理论,构建消防告知承诺管理背景下的消防监管部门与公共场所管理部门的现场核查博弈模型。通过系统均衡点稳定性和数值仿真分析,研究消防监管部门与公共场所管理部门的策略博弈过程。研究结果表明:
(1)由仿真结果可知,随着博弈时间的增加,消防监管部门与公共场所管理部门的博弈系统存在4类可能的演化状态,即“不严格核查、失实承诺”策略组合、“严格核查、失实承诺”策略组合、“不严格核查、如实承诺”策略组合和一种周期反复的演化状态。
(2)消防监管部门的核查力度和公共场所管理部门的如实承诺程度,以及的消防监管部门的核查组织成本、社会信息公开收益、上级消防监管部门的处罚、公共场所管理部门的消防安全投入成本、公共场所受到行政处罚和相关经营损失等是双方策略选择的影响因素。因此,消防监管部门需保持“严格核查”策略以提升公共场所的消防安全水平。同时,要提升消防安全告知承诺管理的核查力度和对公共场所的行政处罚力度,提升公共场所的违法损失感知,促进公共场所管理部门选择“如实承诺”策略。
(3)突出消防执法信息公开既是消防告知承诺管理的必要措施,亦是实施双随机、一公开消防监管与消防安全信用管理的必然要求。为此,消防监管部门需完善信息公开制度并提升信息公开水平,一方面将提升消防监管部门的社会声誉收益感知;另一方面将提升公共场所管理部门的经营损失感知,有效提升消防安全告知承诺管理效能,确保社会面消防安全形势稳定。
