基于ANSYS的锚缆夹具有限元分析*

吴武刚 刘永波 吴家喜 耿合龙

(1.昆明船舶设备研究试验中心 2.海洋石油工程股份有限公司)

0 引 言

石油作为工业的血液，其需求量与日俱增，我国南海石油资源丰富，已然成为重点油气开发中心。浮式生产储油船(FPSO)是一种集储油、处理和卸油等功能于一体的综合油气开发平台，其适用范围广，是具有很强竞争力的海洋设备[1]。锚泊系统作为FPSO重要的定位系统，可以为FPSO提供安全有效的作业状态，因此锚泊系统的安全尤为重要。

目前工程上锚链安全监测方法主要有两种[2]，一种是直接通过压力传感器测量系泊锚链的水平回复力；另一种是通过监测系泊锚链的姿态，利用力学模型通过计算间接得到锚链受到的力，倾角仪就是这样一种监测锚链姿态的设备。本文研究的锚缆夹具是将倾角仪安装于锚缆的水下设备，其一端小管与倾角仪刚性连接，另一端大管通过橡胶夹紧在锚缆上，该夹具已成功应用于“海洋石油119”FPSO的锚泊系统中。目前，对于海洋石油装备类夹具的研究主要集中于海底管道夹具。赵兵杰等[3]利用ABAQUS软件建立了夹具周向密封和径向密封模型，分析了不同摩擦因数下满足密封所需施加的预紧力。刘厚法等[4]研究了长径比对夹具维修点蚀穿孔海底管道压溃性能的影响，分析了海底管道在夹具作用下的抗压溃能力，研究了长径比与夹具压溃压力之间的关系。

本文研究的锚缆夹具属于新式海洋石油装备，目前尚缺乏相关研究。为了保证倾角仪在位运行期间，尤其是在台风期间不至于从锚缆处滑落，夹具设计时必须要有足够大的摩擦力来抵抗自身重力及锚缆运动带来的冲击载荷。本文基于ANSYS软件，建立了该夹具有限元数值分析模型，研究了不同设计参数下夹具能获取的最大静摩擦力。研究结果可为夹具设计及其工程应用提供一定的理论依据。

1 模型理论

为实现夹具与锚缆之间的夹紧功能，使用橡胶圈作为中间零件。一方面，相比于金属与金属，橡胶与金属之间有更大的摩擦因数；另一方面，选择合适硬度的橡胶能够在保持设计夹紧力的同时，保护锚缆免于被夹具挤压破坏。夹具摩擦力的获得主要依靠夹具上的橡胶挤压锚缆获得，在夹具夹紧过程中，橡胶被不断压缩，其变形能力和位移关系已经远远超出了胡克定律的理论范畴，属于典型的几何非线性问题。同时橡胶为超弹性材料，属于材料非线性问题；此外，夹具与夹具、夹具与锚缆之间涉及多个部位之间的接触；故本文夹具夹紧是一个高度的非线性问题，为获得较为准确的计算结果，其中涉及的几何非线性、材料非线性以及接触非线性问题，在有限元模型建立时都必须加以考虑。

1.1 橡胶材料本构模型

目前工程上主要以连续介质力学为基础，橡胶材料被认为是超弹性近似不可压缩体，其力学模型表现为复杂的材料非线性。国内外学者已经提出的用来表征橡胶材料的模型有基于统计热力学的Heo-Hookean应变能函数、Expoential-hyperbolic应变能函数以及基于连续体的表象学方法的Mooney-Rivlin模型，Klosenr-Segal模型和Ogden-Tschoegl模型[5-8]。对于橡胶材料，在变形量小于35%时，目前广泛采用两参数Mooney-Rivlin模型来表征其材料特性，其数学模型表达式如下[9]：

(1)

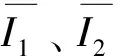
该数学模型很好地描述了变形小于35%的橡胶材料的力学性能，满足橡胶材料实际应用中的性能计算要求。对于使用橡胶材料作为零件设计材料，在材料选型时硬度与压缩量或者压缩率是最重要的两个参数。根据文献[10]，材料模型中的C10、C01两个力学性能常数与弹性模量E、泊松比ν及剪切模量存在某种函数关系，结合文献[11]中的试验数据，可以计算出不同邵氏硬度Hr(IRHD硬度)下，模型分析所需的材料特性数据，结果如表1所示。

1.2 ANSYS库伦摩擦模型

面-面接触单元支持库仑摩擦模型。在基本的库仑摩擦模型[12]中，两个接触面在开始相互滑动之前，在它们的界面上会有剪应力产生，这种状态被称作粘结(stick)状态。库仑摩擦模型定义了一个等效剪应力τ，在某一法向压应力p作用下剪应力一旦超过此值时，表面开始滑动，即有：

τ=μp+COHE

(2)

式中：τ为等效剪应力，μ为摩擦因数，COHE为黏聚应力。

粘合/滑动计算取决于什么时候一个点从粘合状态到滑动状态，摩擦因数可以是任一非负值。程序缺省值为表面之间无摩擦。ANSYS库伦摩擦模型如图1所示。

表1 不同硬度下的橡胶材料特性数据Table 1 Rubber material properties with different hardness

图1 ANSYS库伦摩擦模型Fig.1 Coulomb friction model in ANSYS

2 有限元力学模型建立

为了建立正确有效的力学分析模型，在保证模型合理性的情况下，同时考虑建模方便和节省计算资源，忽略不必要的模型细节，做如下假设：

(1)橡胶材料采用丁腈橡胶，具有确定的弹性模量和泊松比；

(2)橡胶材料拉伸与压缩的蠕变性质相同；

(3)蠕变不引起体积变化，故橡胶可看成不可压缩材料；

(4)倾角仪不是主要分析对象，模型中仅考虑重力和惯性作用，故建模时以质量单元mass21代替；

(5)模型中的倒角与销孔等不影响整体强度和分析的细节，建模时不予考虑。

基于上述假设，建立了夹具有限元分析模型，其网格划分如图2所示。模型中网格采用扫掠网格划分方式，以生成六面体网格为主，六面体网格在较少网格的情况下也可得到精确的计算结果。单元类型选择支持超弹性变形的solid186单元，该单元有20个节点，能准确模拟橡胶的变形特性。接触单元采用targe173和conta174单元，该3D面-面接触单元支持上述的标准库伦摩擦模型。建立的有限元模型包含实体单元 、接触单元以及质量单元，共计20 458个单元。

1—锚缆段；2—橡胶圈；3—夹具主体；4—螺杆；5—加强筋板。

3 结果分析

为了从理论上验证该夹具设计的合理性及工程施工操作的可行性，本文从夹具强度、接触压力、最大静摩擦力、螺杆预紧力及扭矩施加等角度，对夹具进行一个全面的有限元分析。模型钢缆直径固定值为155 mm，选取夹具长度的2倍(即1.2 m)锚缆段进行分析，此参数适用以下所有分析。

3.1 强度分析及最大摩擦力研究

本文选取中等偏下硬度(50 HD)的橡胶进行分析，研究厚度为22.5 mm，宽度为50 mm的橡胶圈，径向压缩3 mm，对应压缩率为13.3%时 ，夹具、螺杆的受力及变形情况。模型加载共分3个载荷步：第一个载荷步施加橡胶过盈接触，使橡胶接触单元偏移到锚缆外径处，模拟橡胶圈夹紧钢缆的过程；第二个载荷步施加重力载荷，模拟夹具水下工作状态；第三个载荷步继续施加锚缆轴向力，直至钢缆发生较大滑移，以便获取最大静摩擦力。本文假定最大静摩擦力近似等于滑动摩擦力。

图3为夹具夹紧后的Von Mises应力和变形云图，其中变形云图为柱坐标系下的UY方向位移值。从图3可以看出，夹具在上、下橡胶夹紧位置处有较大的应力区，此处应力主要来源于橡胶反弹作用力，且夹具的最大应力发生在加强筋板的外边缘处，约为46.31 MPa，此应力值远小于钛合金1 012 MPa的屈服强度值，因此夹具强度能够满足设计要求。尽管夹具的应力水平较低，但从应力分布来看，最大应力并没有发生在夹具夹钢缆的主体管内，筋板起到有效的保护夹具主体度的作用。从UY位移值可以看出，尽管螺栓使用很大的预紧力，但夹具端部并不能完全闭合，仍然有约0.85°的张开角度。此处易因橡胶圈挤压力过大，导致橡胶被挤入此处间隙而引起橡胶损伤，因此夹具不宜选择压缩量太大的橡胶来产生摩擦力。实际工程应用时，在水下操作允许的情况下可以使用螺钉闭合此处间隙。

图3 夹具夹紧后的Von Mises应力及变形云图Fig.3 Von Mises stress and deformation contour after clamping

橡胶圈挤压变形云图如图4所示。由图4可知，由锚缆径向从外到内，橡胶圈挤压变形逐渐增大，最大值为3.1 mm。在挤压过程中，橡胶变形会沿锚缆轴向发生，橡胶圈被挤压向上变形量为1.2 mm，同时在重力作用下，橡胶圈向下最大位移为2.38 mm。

橡胶上、下变形突起位移值并不相等，进而使得摩擦应力也分布不均，橡胶圈下部摩擦应力最大为0.19 MPa，最小应力区发生在中部偏上位置。橡胶圈摩擦应力云图如图5所示。

图4 橡胶圈挤压变形云图Fig.4 Compressional deformation contour of rubber ring

图5 橡胶圈摩擦应力云图Fig.5 Friction stress contour of rubber ring

图6为螺杆应力分布云图。从图6可知，螺杆的最大应力为34.576 MPa，螺杆的应力并没有像只有预紧力作用时分布的那么均匀，最大应力发生在两半夹具接触面稍往外处，此处应力产生除螺杆预紧力之外，其主要是来自于螺杆受到夹具的弯曲作用。从螺杆应力分布结果可以看出，通过扭力扳手施加给螺栓的预紧力并不全部用于橡胶圈的夹紧，还有相当大一部分预紧力用来抵抗夹具的弯矩作用。从结构力学角度分析，螺杆的预紧力与橡胶圈的反弹作用力形成一个平衡力偶，施加的螺杆预紧力到底有多少效率用于橡胶夹紧与两者的作用距离有关。

图6 螺杆应力分布云图Fig.6 Stress contour of screw

为了验证力学模型和获取夹具的最大静摩擦力，选取橡胶中心处的单元，分析其滑移量与摩擦力轴向分量之间的关系，结果如图7所示。由图7可知：在橡胶夹紧的载荷步中，此时没有外力作用，橡胶中心处不发生滑移，也没有产生摩擦力；随后在逐步施加重力的过程中，橡胶圈中心处开始滑移并产生摩擦力，虚线处为重力加载完毕，对应的滑移量为0.389 mm，摩擦力锚缆轴向分量为586.7 N。用ANSYS循环计算除锚缆外的每个单元质量，并累计施加的质量单元可得有夹具有限元模型总质量为59.9 kg，故模型夹具理论重力为587.0 N，同时再提取此载荷步最后子步锚缆轴向的支座总反力，结果为586.9 N；三者几乎相等，说明通过不断施加力使夹具产生滑移来获取最大摩擦力的方法可行。由图7还可以看出，随着滑移量逐渐增加到3 mm(此时可认为夹具已经滑动)，摩擦力趋向于一个定值，此值便是滑动摩擦力。基于前面假设，得到夹具能够获得的最大静摩擦力约为2 260.0 N，为其重力的3.85倍，故夹具能够承受的最大冲击载荷为3.85G(G为夹具重力)。

图7 橡胶中心处单元滑移量与摩擦力的关系曲线Fig.7 Relationship between friction force and slip of element in rubber center

3.2 不同硬度橡胶材料的影响

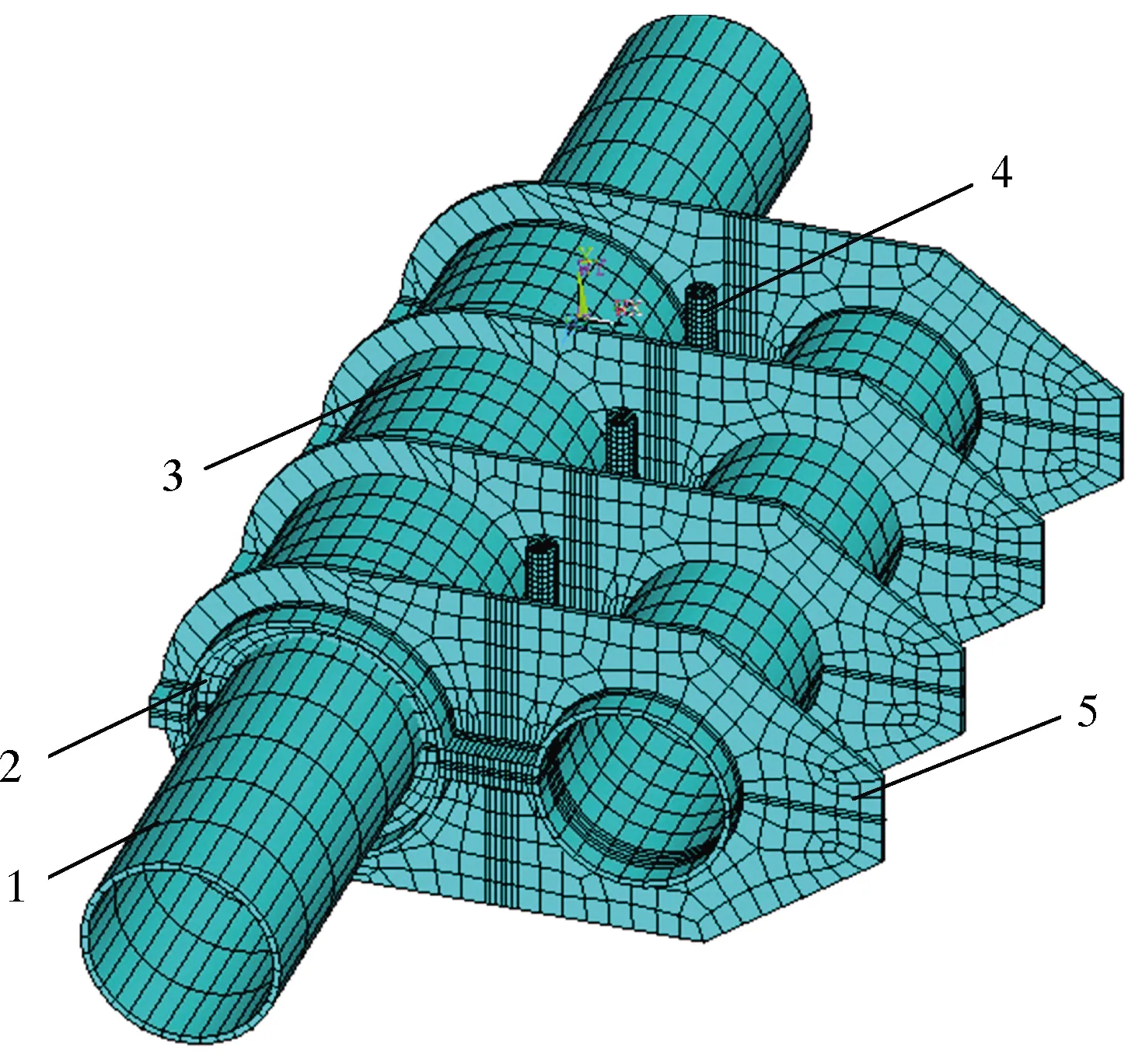
丁腈橡胶材料的邵氏硬度范围一般为40～80 HD，在受零件尺寸限制时，橡胶的设计压缩量往往接近一个定值，因此要获得合适的摩擦力，必须选择合适硬度的橡胶。本文共分析了压缩量为3 mm，橡胶宽度为50 mm时，使用6种不同硬度的橡胶材料，夹具能够获得的最大摩擦力和螺杆所需施加的预紧力。不同硬度下的最大静摩擦力如图8所示。

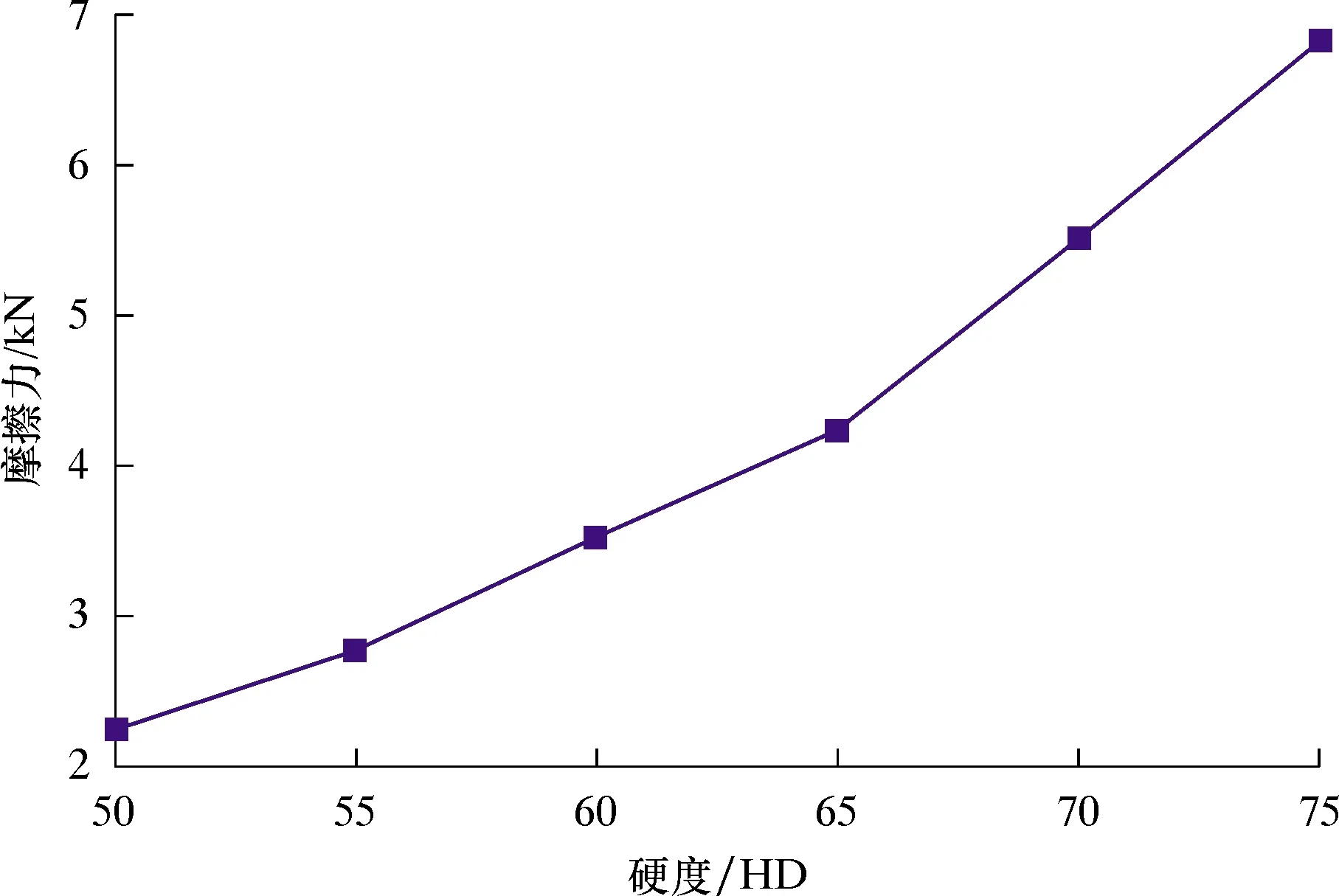
图8 不同硬度下的最大静摩擦力Fig.8 Maximum static friction force with different hardness

由图8可知：当橡胶压缩量相同时，最大静摩擦力随着材料硬度的增加而增大，且呈现出非线性，趋势近似于二次曲线；橡胶硬度为75 HD时，夹具能获得的最大静摩擦力约为6 815 N，此时橡胶施加在锚缆上的压力为18 271 N，其产生的应力为1.58 MPa。

不同硬度下的橡胶压力和螺杆轴力如图9所示。从图9可以看出，获得最大静摩擦力所需的橡胶压力和螺杆轴力(通过扭力扳手施加扭矩获得)随着橡胶硬度的增加，也呈现出二次增长趋势，且螺杆轴力始终大于橡胶压力，计算二者在不同硬度下的比值分别为0.626 2、0.624 7、0.626 2、0.621 6 、0.621 3和0.625 0。由此可见，螺杆预紧力能有效传给橡胶施加压力，从而产生摩擦力的效率大约为62%。

图9 不同硬度下的橡胶压力和螺杆轴力Fig.9 Rubber pressure and screw axial force with different hardness

3.3 不同橡胶压缩量的影响

压缩量是影响最大静摩擦力的另一重要参数。系泊锚链铺设完成后，上部锚缆段受水压及下部锚链的重力作用，锚缆直径必然变小，实际施工后锚缆直径很难准确界定，而锚缆直径又是夹具设计时的一个重要参数，因此有必要研究一定范围压缩量下的最大静摩擦力。本文选取硬度为50 HD，压缩量分别为1.5、2.0、2.5、3.0、3.5以及4.0 mm进行分析，该范围内橡胶的压缩率为6.67%～17.78%，此压缩率下，两参数的Mooney-Rivlin模型能够较好地模拟橡胶的力学特性。计算结果如图10和图11所示。

由图10可知：最大静摩擦力随着压缩量的增加而增大，且近似呈线性关系；当橡胶圈径向压缩量增加到4.0 mm时，夹具能获得的最大静摩擦力为2 832 N。相对硬度的增加，压缩量给最大静摩擦力带来的增加相对较小，即当压缩量在较小范围内时，最大静摩擦力也将维持在一个相对稳定的值，不会出现摩擦力剧烈增大的情况。由图11可知，随着压缩量的增大，螺杆轴力和橡胶压力呈线性增加，且螺杆轴力增加更快。计算二者在不同压缩量下的比值，分别为0.641 8、0.640 0、0.634 6、0.626 2、0.624 9和0.621 4，由此可见，螺杆预紧力能够有效传给橡胶施加压力，而产生摩擦力的效率随着压缩量的增加略微有所减小。

图10 不同压缩量下的最大静摩擦力Fig.10 Maximum static friction with different compression

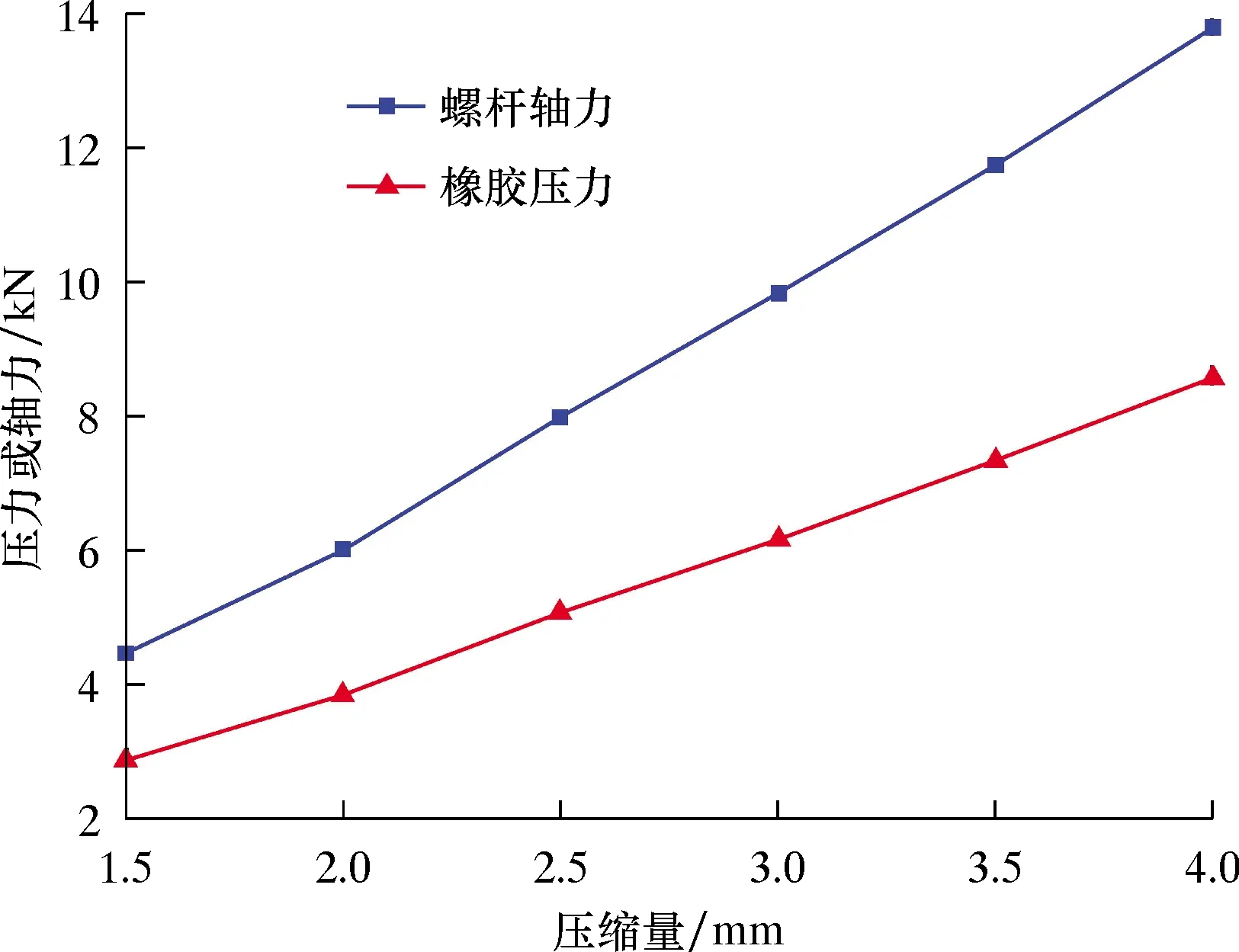
图11 不同压缩量下的橡胶压力和螺杆轴力Fig.11 Rubber pressure and screw axial force with different compression

4 结 论

根据锚缆倾角仪夹具的工程实践，采用有限元分析软件ANSYS对夹具进行数值模拟，研究了夹具和螺杆的应力分布情况，通过施加滑移，分析了橡胶的接触压力和接触摩擦应力，得到了夹具工作状态所能获得的最大静摩擦力。此外，进一步研究了橡胶材料的硬度和橡胶压缩量对最大静摩擦力的影响，以及对螺杆预紧力用于产生摩擦力效率的影响，得出以下结论：

(1)加强筋板外边缘处应力最大，一定程度上分散了夹具主体管件的应力，且夹具整体应力处于较低水平。

(2)选取邵氏硬度为50 HD，压缩量为3 mm的橡胶，对应压缩率为13.3%时，夹具产生的最大静摩擦力能使夹具承受约3.85G(G为夹具重力)的冲击载荷。

(3)最大静摩擦力和螺杆所需预紧轴力均随着橡胶材料硬度的增加而快速增大，其变化关系近似于二次曲线。随着橡胶压缩量的增加，最大静摩擦力、螺杆所需预紧轴力也呈线性增大。

(4)螺杆预紧轴力并不能全部用于挤压橡胶而产生摩擦力，其效率与模型参数有关，本文研究的夹具螺栓预紧轴力效率约为62%。结合扭矩输出轴力的效率，可以计算出最大静摩擦力对应夹具安装时所需施加于螺杆上的扭矩。