超高密度油基钻井液井筒循环温度场模型研究*

2021-11-16徐新纽甘仁忠

石油机械 2021年11期

阮彪黄鸿徐新纽甘仁忠张伟杨虎

(1.中国石油新疆油田分公司勘探事业部 2. 中国石油大学(北京)克拉玛依校区)

0 引言

我国新疆油田、塔里木油田、川东油气田和南海莺琼盆地等[1]都存在高温高压地层钻井时井底压力难以精确控制的问题。其原因就是超深井井筒内钻井液密度和流变性不再是一个常数，而是随钻井液温度和压力的变化而变化。因此，能否准确描述钻井液温度沿井深的变化规律及其对压力的影响，关系到钻井工程的成败。

准噶尔盆地南缘地区深部地层温度和压力分别达到164 ℃和133 MPa，油基钻井液是解决南缘巨厚泥岩安全钻井的有效手段[2-3]。但油基钻井液密度和流变性受温度和压力影响较大[3]。其中，高泉背斜高102井呼图壁河组(井深5 575.49 m)为高压窄密度窗口的含水薄砂层，预测地层压力系数为2.21～2.28，地层漏失压力系数为2.36。前期采用钻井液密度为2.21 g/cm3，依据传统地层温度代替循环温度的方法，计算出井底钻井液循环当量密度为2.30 g/cm3(若采用循环热交换温度，计算井底钻井液循环当量密度为2.26 g/cm3)，认为可以安全钻揭该地层。但该地层钻进时，钻时由18 min/m降至3 min/m，地层出水量为30 m3，造成井壁泥岩水浸后严重坍塌。随后将钻井液密度调整为2.25 g/cm3，实现安全钻井。因此，对于窄密度窗口的复杂地层，为确保高温高压深井井底压力的准确计算及安全施工，需要研究高温深井钻井液循环温度计算模型，从而精确模拟环空钻井液的实际温度，为井底当量密度和井底压力有效控制提供科学依据。

1969年，L.R.RAYMOND[4]研究了钻井循环过程中井筒钻井液及地层温度场的变化规律。R.J.SCHOEPPEL等[5]应用L.R.RAYMOND模型首次将温度对流体特性参数的影响引入计算过程，并研究了简单井身结构情况下钻井液及地层的温度分布规律。1973年，H.H.KELLER等[6]首次提出了多层套管结构下井筒循环钻井液温度的分布规律，并且详细地给出了井筒内各界面上对流换热系数的计算方法。1984年，B.CORRE等[7]为了探讨温度对井壁稳定性的影响，应用数值模拟方法研究了钻井井筒及地层温度场的变化规律。近10年来，杨虎、王轲和何淼等[8-10]在L.R.RAYMOND模型的基础上，考虑钻井液温度、密度及压力等3个参数相互关联，将深井井筒的温度场和压力场进行耦合处理，利用有限元等数值解法进行求解。但是，前人模型中的流体介质多为水基钻井液，并未考虑油基钻井液以及窄间隙环空在钻井液高返速条件下产生的摩擦内热源项，计算结果不满足窄安全密度窗口深井或超深井的钻井技术要求。因此，需要研究考虑摩擦内热源的油基钻井液的深井井筒循环温度计算模型。

1 油基钻井液井筒循环温度模型

钻井过程中，由于不同深度处地层温度不同，钻井液与地层之间存在温度差，钻井液与地层发生热交换，具体表现为钻井液和地层温度不断变化，所以井筒内温度场是一个非稳态的变化过程。

1.1 物理模型

首先建立井筒钻井液循环时井筒物理模型(见图1)，将整个井筒分为5个区域[8-10]，分别为钻柱内、钻柱、环空、套管和地层(包括水泥环)。区域1钻井液向下稳定流动，区域3钻井液向上流动。井筒径向区域间热量传递符合热力学与传热定律，轴向各区域内符合能量与物质守恒定律。

图1 钻井液循环时井筒物理模型Fig.1 Physical model of wellbore during drilling fluid circulation

为了研究循环过程中地层温度对钻井液性能的影响，将钻井液在井眼中的循环传热过程分为3个阶段：①由地面进入钻柱，经钻柱向下流动；②钻井液在井底通过钻头由钻柱进入环空；③钻井液通过环空向上流动到达地面。

在第1阶段，钻井液以给定的温度TD0进入钻杆向下流动，其温度由沿钻柱方向的热对流速率及钻柱与环空之间的热传递速率和时间决定；在第2阶段，如果忽略钻井液经过钻头时热能的增量，则认为井底的环空与钻柱内钻井液温度相同，即TD(H,t)=TA(H,t)；在第3阶段，钻井液向上流动，其温度由钻井液与钻柱及地层的热交换率和时间决定。

1.2 传热控制方程

假设条件：①钻井液的轴向热传导与轴向对流相比可以忽略不计；②钻井液的比热容、密度和热传导系数等参数随温度变化的程度不显著；③钻柱和套管均为钢材，热传导性好，传热过程中钻柱和套管无热量损失。于是，井筒钻井液及地层的温度场可由控制方程(式(1)～式(3))和补充方程(式(4))组成。

钻柱内：

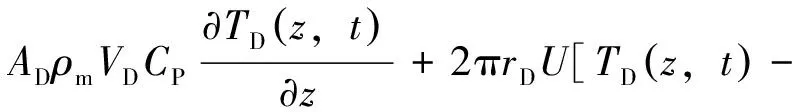
(1)

环空内：

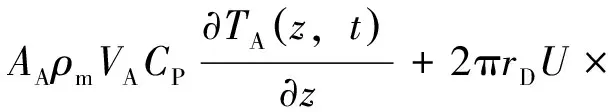
(2)

地层内：

(3)

井壁上：

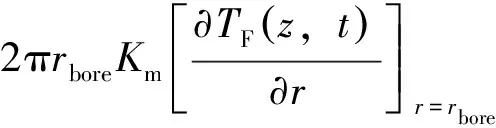
(4)

式中：TD为钻柱内钻井液温度，℃；TA为环空钻井液温度，℃；TF为地层温度，℃；AD、AA分别为钻柱内和环空横截面积，m2；vD、vA分别为钻柱内和环空内钻井液流速，m/s；ρm、ρf分别为钻井液密度和地层密度，kg/m3；CP、CPf分别为循环钻井液比热容和地层比热容，J/(kg·℃)；rD、rbore分别为钻柱中径半径和井眼半径，m；Km为地层热传导系数，W/(m·℃)；hf为井壁对流换热系数，W/(m2·℃)。

1.3 边界及初始条件

控制方程的边界条件如下。

钻井液入口温度已知，即：

TD(z=0,t)=TDo(t)

(5)

式中：TDo为钻井液地面温度，℃。

在井底，钻柱内钻井液温度与环空钻井液温度相等，即：

TD(z=L,t)=TA(z=L,t)

(6)

地层无穷远处温度等于同一深度原始地层温度，即：

TF(r∞,z,t)=TF(z)

(7)

初始条件：假设在初始时刻地层和井筒内的温度为原始地层温度，即：

TD(z,0)=TA(z,0)=TF(r,z,0)=TF(z)

(8)

1.4 补充方程

上述井筒循环物理模型和传热控制方程完全适用于不同配方的水基钻井液和油基钻井液。针对不同类型钻井液配方中各组分的热物理参数，利用各组分体积分数的复合函数关系，求解相应配方钻井液的热物理参数。笔者以准噶尔盆地南缘高探1井高密度油基钻井液为例，将钻井液的定压比热容和对流换热系数视为其主要组分(包括柴油、水和重晶石)热物理参数(见表1)的复合函数。

表1 油基钻井液各组分热物理参数Table 1 Heat conduction parameters of components in oil-based drilling fluid

1.4.1 定压比热容Cp

由于高探1井油基钻井液中油水比约为90∶10，油水混合物的Cp≈Cpo。加重钻井液的固相体积分数约为：

SF=0.037(ρm-1 000)

(9)

因此，加重油基钻井液的定压比热容公式为：

Cp=Cpo(1-SF)+CpsSF

(10)

式中：SF为钻井液固相体积分数；Cpo、Cps分别为油相和固相(加重材料)定压比热容，J/(kg·K)。

1.4.2 对流换热系数

钻柱与环空、环空与井壁(套管内壁)之间的对流换热系数Udp、Uann分别为[11-12]：

(11)

(12)

其中：

hdp=hann=(1-SF)ho+SFhs

(13)

式中：hdp为钻柱内钻井液的对流换热系数，W/(m2·℃)；hann为环空钻井液的对流换热系数，W/(m2·℃)；ho为钻井液中基油的对流换热系数，W/(m2·℃)；hs为钻井液中加重材料的对流换热系数，W/(m2·℃)；Ksteel为钢材热传导系数，W/(m·℃)；ri为钻柱内壁半径，m；ro为钻柱外壁半径，m；Ri为套管内壁半径，m；Ro为套管外壁半径，m；rbore为井壁半径，m。

2 内热源项的确定

钻井过程中，钻井泵和旋转系统分别提供水力能量和机械能量。其中，部分能量用于破碎岩石和携带岩屑返出井筒，剩余能量以热量的形式耗散，直接影响井筒温度分布[12]。热源项主要包括以下3部分：钻井液流动黏性耗散产生的热量、钻柱与井壁旋转摩擦产生的热量和钻头破岩产生的热量。

2.1 钻井液黏性耗散热

针对非牛顿流体的流动特性，钻井液黏性耗散产生的热量主要表现在循环摩阻压降，由钻柱旋转产生的螺旋流动使摩阻压降的计算更加复杂。依据樊洪海等[13-15]采用赫巴流变模式建立的摩阻压降模型和易灿等[16]、罗伟等[17]提出的钻柱摩阻扭矩模型，采用雷诺数Re及泰勒数Ta来描述旋转对摩阻压降产生的影响，建立了钻柱旋转与非旋转摩阻压降比值的经验校正方法。因此，钻井液黏性耗散热表达式为：

Qc=RwΔpfQ

(14)

式中：Qc为摩阻压降生热量，kW；Δpf为流动摩阻压降，kPa；Q为钻井液流量，m3/s。

钻柱旋转摩阻压降比值Rw的定义为：

(15)

式中：τ为赫巴流变模式的屈服值，Pa；v为钻井液流速，m/s；ε为偏心率；n为赫巴流变模式的流性指数；κ为井眼直径与钻柱外径的比。

2.2 钻柱与井壁摩擦生热和钻头破岩生热

EYMARD认为钻机提供的机械能一部分消耗于破碎岩石，占总机械能的10%。其余90%的机械能产生了热量，其中60%消耗在钻柱与井壁的摩擦上，40%消耗在钻头与地层的摩擦上[18-20]。钻机提供的机械能计算式为：

W=Tω

(16)

式中：W为机械能，W；T为转盘扭矩，N·m；ω为转盘转动角速度，rad/s。

3 数值求解

为了确保解的稳定性，采用全隐式差分方法对控制方程进行数值离散。井筒温度场有限差分的网格划分见图2。

图2 井筒温度场有限差分的网格划分示意图Fig.2 Mesh generation of finite difference method for wellbore temperature field

由于地层向井壁的径向热传导变化剧烈，而等距离散会造成井壁附近网格划分过于稀疏，势必影响求解精度，所以设r=rboreexp(x)，对地层内的非稳态热传导方程进行变换，对变量x进行等距离散，可实现对井壁周围地层合理的离散，井壁周围网格划分较密，随着向地层深部延伸，温度变化平缓，网格变得稀疏。

4 实例计算

高探1井为准噶尔盆地南缘地区的重要发现井。该井采用ø13 mm油嘴试油，日产原油1 213 m3、天然气32.17×104m3，成为国内陆相碎屑岩储层首口千吨井。高探1井储层为白垩系齐古组，储层压力为134 MPa，完钻井深5 920 m，采用四开井身结构(见表2)。

表2 高探1井井身结构Table 2 Casing program of Well Gaotan 1

4.1 模拟条件

预测四棵树凹陷高泉东断背斜每100 m地温梯度为2.21 ℃，高探1井井底地层温度为137.63 ℃。四开钻具组合为ø215.90 mm PDC钻头+ø158.75 mm钻铤2根+ø214.00 mm稳定器+ø158.75 mm钻铤20根+ø159.00 mm随钻震击器1根+ø158.75 mm钻铤1根+ø127.00 mm加重钻杆18根+ø127.00 mm钻杆75根+ø139.70 mm钻杆。油基钻井液密度为2.34 g/cm3，塑性黏度为132 mPa·s，动切力为17 Pa，排量为10～13 L/s，四开井段平均机械钻速为1.51 m/h。

4.2 模拟结果

高探1井四开钻进至5 920 m，排量为11 L/s，钻井液入口温度34.2 ℃时，钻井液循环达到稳态后，模拟钻井液出口温度为36.76 ℃，在井深5 311 m处环空钻井液温度达98.69 ℃(见图3)。

应用本文模型和L.R.RAYMOND模型分别计算了钻进至不同井深处的循环温度，将环空出口温度的计算值与实测值进行对比，本文模型的计算值与实测值误差较小(见表3)。

4.3 敏感性分析

当高探1井四开油基钻井液配方及性能不变时，井筒循环温度的主要影响因素为钻井液排量和密度。因此，分析了钻井液排量为13～28 L/s时，井筒达到稳态的环空循环温度变化情况(见图4)。由图4可知：当钻井液排量小于21 L/s时，随着钻井液流量增大，井底环空温度逐渐降低；当钻井液排量大于21 L/s时，下部环空钻井液循环温度出现由冷却效应向摩擦增温效应转变的“拐点”。井筒循环内热源的影响明显较大，流体与井壁、钻柱产生的黏性摩阻显著增加(尤其是窄间隙环空段)。其原因是井深4 900～5 430 m采用ø244.50 mm套管固井，环空间隙较窄，且裸眼井段的大尺寸钻铤使环空更窄。钻井液流量越大，这些窄间隙环空流速越高，井底环空钻井液温度逐渐升高。

图3 高探1井四开油基钻井液循环温度剖面Fig.3 Circulating temperature profile of oil-based drilling fluid in fourth spud of Well Gaotan 1

表3 高探1井四开钻井液出口温度模拟结果
Table 3 Simulation results of drilling fluid outlet temperature in fourth spud of Well Gaotan 1

井深/m排量/(L·s-1)入口温度/℃出口温度/℃实测值L.R.RAYMOND模型计算值本文模型计算值5 8001333.737.234.1335.375 8201233.937.233.4435.475 8401132.535.832.2133.675 8601232.335.133.0133.565 9001133.835.933.9834.355 9201134.236.134.1636.76

钻井液密度对环空循环温度的影响较大(见图5)。由式(10)和式(13)可知，钻井液密度越大，其固相体积分数越大，钻井液的定压比热容和对流换热系数增大，导致井筒钻井液温度升高。另外，井筒循环内热源模型(式(14))中，流体与井壁、钻柱产生的黏性摩阻与钻井液密度呈正相关。因此，同一井深处的钻井液循环温度随着密度的增加而升高。