电励磁凸极同步电机磁阻转矩及其利用率提升方法研究

付兴贺，江政龙，陈 锐

(东南大学 电气工程学院，南京 210096)

0 引 言

自20世纪80年代钕铁硼问世以来，永磁电机发展迅速，因其具有体积小、质量轻等优点,被广泛应用在电动汽车、航空航天等各个领域[1]。和电励磁电机相比，永磁电机存在一些结构和成本上的劣势，如永磁体高温退磁、永磁磁链固定不易调节、钕铁硼价格昂贵等。因此，近年来电励磁电机又重新进入人们的视野。传统的电励磁电机(以下简称WFSM)和永磁电机相比存在一些缺陷。一方面，WFSM在结构上存在电刷和滑环，而电刷和滑环由于机械和电气等方面的原因容易摩擦而致损坏；另一方面，WFSM转子侧绕线的存在增加了一部分转子铜耗。采用无线传输技术，WFSM可以免去电刷和滑环，并且励磁侧传输效率可以达到85%[2]。本文改进了传统WFSM的转子结构，提升电机磁阻转矩及其利用率，从而在输出总转矩一定的情况下减小励磁电流。

电励磁凸极电机的输出转矩由两部分组成：一是定转子磁动势相互作用形成的励磁转矩；二是d，q轴之间的电感差形成的磁阻转矩。励磁转矩和磁阻转矩达到最大值时对应的电流角不同，在传统WFSM(Ld>Lq)中，励磁转矩在电流角为0时达到最大值，磁阻转矩在电流角为-45°时达到最大值。在电流角一定的情况下，电机输出的总转矩是励磁转矩和磁阻转矩的代数和，因此提升磁阻转矩可以在定转子电流不变的前提下提升总转矩，从而提升转矩密度。磁阻转矩近似和d，q轴电感差成正比，因此，提高磁阻转矩可以转化为增大d，q轴电感差(或增大凸极率)，常用方法是在转子侧设置磁障[3-7]。Lipo T A教授团队提出三种带有磁障的转子结构拓扑，并对单磁障的情况做了深入分析。有限元分析表明，磁障宽度占转子极宽的7%时总转矩提升效果最佳[4]。实际上，磁障宽度到达一定值会加剧d轴磁路饱和程度，导致d轴电感下降明显，不利于磁阻转矩的提升[5]。因此，文献[6-7]在设置磁障的同时增加WFSM的转子极的宽度来缓解饱和对凸极率的影响。文献[8]研究转子肋宽和磁障宽度对d，q轴电感的影响。仿真结果表明，适当长度的肋宽和磁障宽度可以对d轴磁路产生隔磁作用，从而加剧d轴磁路的饱和程度，减小d轴电感，但磁障宽度过大又会加剧q轴磁路的饱和程度，减小q轴电感，影响转矩输出。除此之外，凸极率受磁障的条数和形状的影响较大，最高甚至能达到50%[9]。为了进一步提升总转矩，可以使用磁偏置技术，即通过改进电机的转子结构，减小励磁转矩和磁阻转矩达到最大值时的电流角差[10-12]，从而提升磁阻转矩的利用。文献[13]对一台混合励磁电机转子结构进行改进，使励磁转矩最大值和磁阻转矩最大值对应的电流角相等，从而总转矩得到提升。

本文研究一种带磁障的电励磁电机(以下简称WFSMFB)拓扑结构，并运用磁路法和相量图，推导WFSMFB的转矩表达式，定性分析了磁障宽度对磁阻转矩的影响。针对不同磁障类型，对单条磁障和双条磁障模型进行有限元仿真，在设置磁障的前提下给出d轴磁路导磁面积减小、d轴磁路导磁面积不变(对称转子)、d轴磁路导磁面积不变(不对称转子)三种情况下的仿真结果，对磁障宽度的选取进行了定量研究。在此基础上，在磁障内放入永磁体，通过调整永磁体的充磁方向实现磁偏置，减小励磁转矩和磁阻转矩达到最大值时的电流角差，从而提升磁阻转矩的利用率。

1 WFSMFB拓扑结构与转矩方程

1.1 WFSMFB结构

本文研究的WFSMFB定、转子结构如图1所示。该电机的极槽配合为4极36槽，定子侧绕组形式为分布式短距绕组，定子材料为DW310-35，转子材料为10号钢，磁障中心线和转子极中心线重合。WFSMFB的结构参数如表1所示。

表1 WFSMFB结构参数

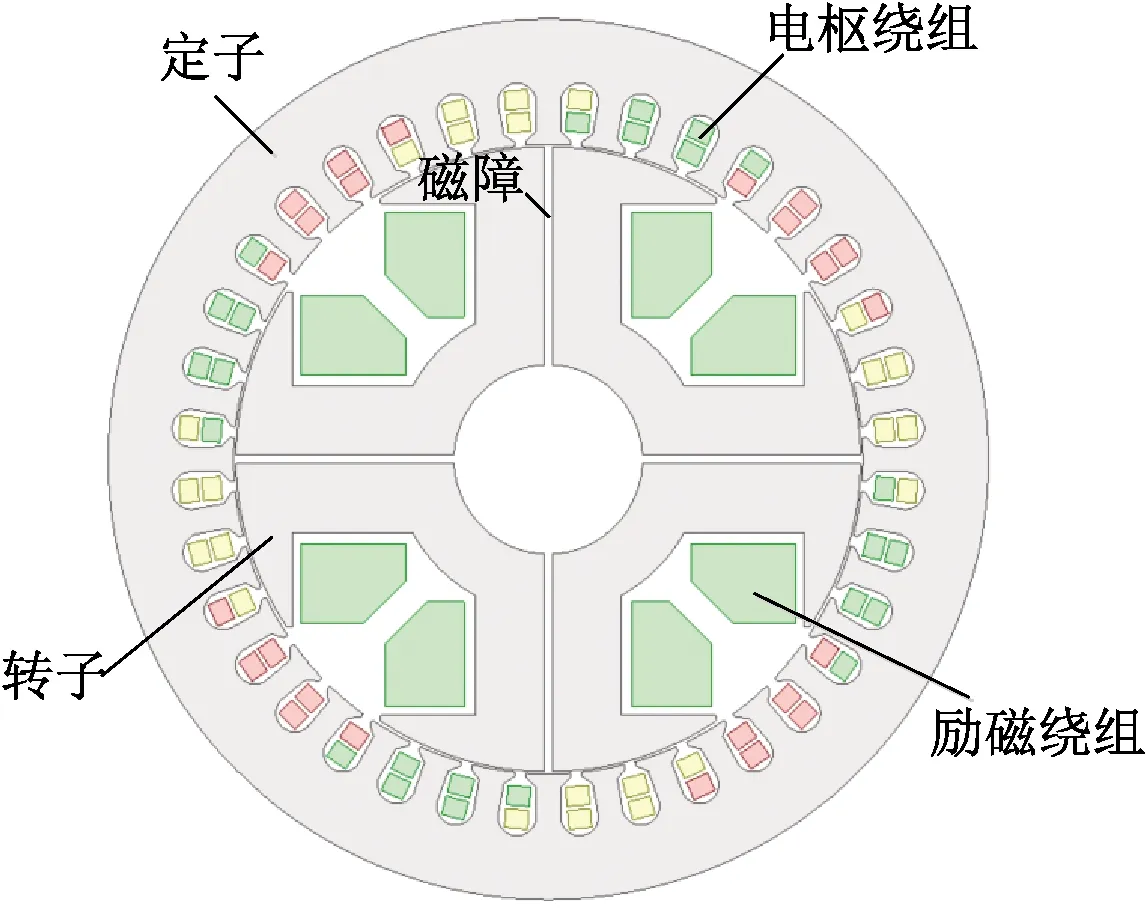
图1 WFSMFB定转子结构图

1.2 WFSMFB电磁转矩表达式

WFSMFB的d，q轴坐标系中，d轴方向为转子励磁绕组轴线的中心线方向，而q轴超前d轴90°电角度，d，q轴坐标系下的相量图如图2所示。

图2 WFSM在d，q轴坐标系下的相量图

在d，q轴坐标系下的功率方程如下：

(1)

式中：P为电机轴端的输出功率；ωe为电角速度；ψd,ψq为d，q轴磁链；id,iq为d，q轴电流。

由功率方程可推出转矩方程：

(2)

式中：T为转轴上的输出转矩；ψf为励磁磁链；p为电机极对数；is为电枢电流有效值；γ是电枢电流角；Ld,Lq为d，q轴电感。

为了定性分析磁障对磁阻转矩的影响，运用简化磁路法分析WFSMFB的d，q轴磁路，如图3所示。

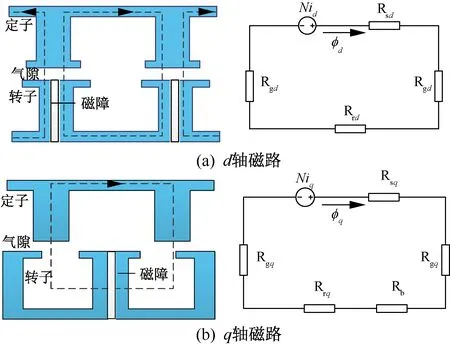
图3 WFSMFB的d,q轴简化磁路图

图3(a)中q轴磁动势可以表示：

Fq=Niq=φq(2Rgq+Rsq+Rb+Rrq)

(3)

式中：Fq为q轴磁动势；iq为q轴电流；φq为q轴磁通；Rgq为q轴磁路对应的气隙磁阻；Rsq为q轴磁路对应的定子侧磁阻；Rrq为q轴磁路对应的转子侧磁阻；Rb为磁障对应的磁阻。

若设置磁障时增加转子极两侧的宽度，则d轴磁动势可以表示：

Fd=Nid=φd(2Rgd+Rsd+Rrd)

(4)

式中：Fd为d轴磁动势；id为d轴电流；φd为d轴磁通；Rgd为d轴对应的气隙磁阻；Rsd为d轴磁路对应的定子侧磁阻；Rrd为d轴磁路对应的转子侧磁阻。

根据式(3)和式(4)可得d,q轴电感：

(5)

(6)

将式(5)和式(6)代入式(2)中，则磁阻转矩表达式：

(7)

从式(7)可以看出，磁障磁阻是影响WFSMFB磁阻转矩的关键因素。磁障磁阻可表示：

(8)

式中：μ0为真空磁导率；μr为相对磁导率；lb为磁障的长度；l为电机轴向长度；wb为磁障宽度。

本文设置的磁障贯穿转子极，磁障宽度是影响磁障磁阻的关键。

2 磁障设计及仿真分析

本文以输出转矩为目标，对单磁障和双磁障模型进行有限元仿真分析，计算以下三种情况的磁障的合理尺寸：d轴磁路导磁面积减小、d轴磁路导磁面积不变(对称转子)、d轴磁路导磁面积不变(不对称转子)。

2.1 d轴磁路导磁面积减小时的磁障设计

d轴磁路导磁面积减小时的转子结构如图4所示。图4中，wp为转子极宽度，wb为磁障宽度，wbg为两条磁障之间的宽度。

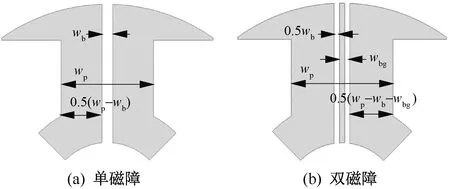
图4 不增加转子极宽度时的转子结构图

图5(a)为单磁障情况下总转矩和磁阻转矩随磁障宽度的变化趋势。磁障对q轴磁路有一定的隔磁作用，但磁障宽度过大会加剧d轴磁路和励磁磁路的饱和程度，d轴电感和励磁磁链都会减小。因此，总转矩和磁阻转矩都呈现先增大后减小的趋势。有限元分析表明，当磁障宽度为2 mm，即占转子极宽的5.7%时，总转矩相比于不设置磁障时提升最多。

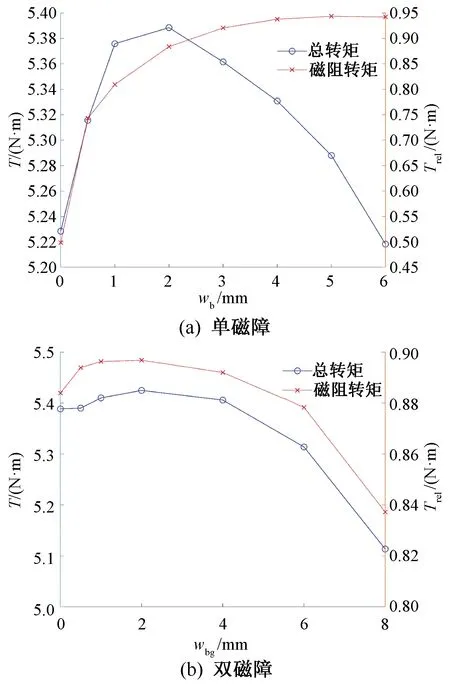
图5 不增加转子极极宽时的总转矩、磁阻转矩变化情况

双磁障情况的分析基于单磁障展开，磁障的总宽度为2 mm，两条磁障左右对称分布，对磁障之间的距离做参数化分析，如图5(b)所示。仿真结果表明，适当增加磁障之间的距离能提升总转矩，并且磁障之间的距离为2 mm，即占转子极宽的5.7%时，总转矩提升最多。通过对比两种情况发现，双磁障情况在总转矩提升方面优于单磁障。为了方便分析，在后两种情况中磁障之间的宽度取2 mm。

2.2d轴磁路导磁面积不变(对称转子)时的磁障设计

为了缓解磁障对d轴磁路的影响，设置磁障时固定d轴磁路的导磁面积，即在转子极两侧增加极宽，对应的转子结构如图6所示。

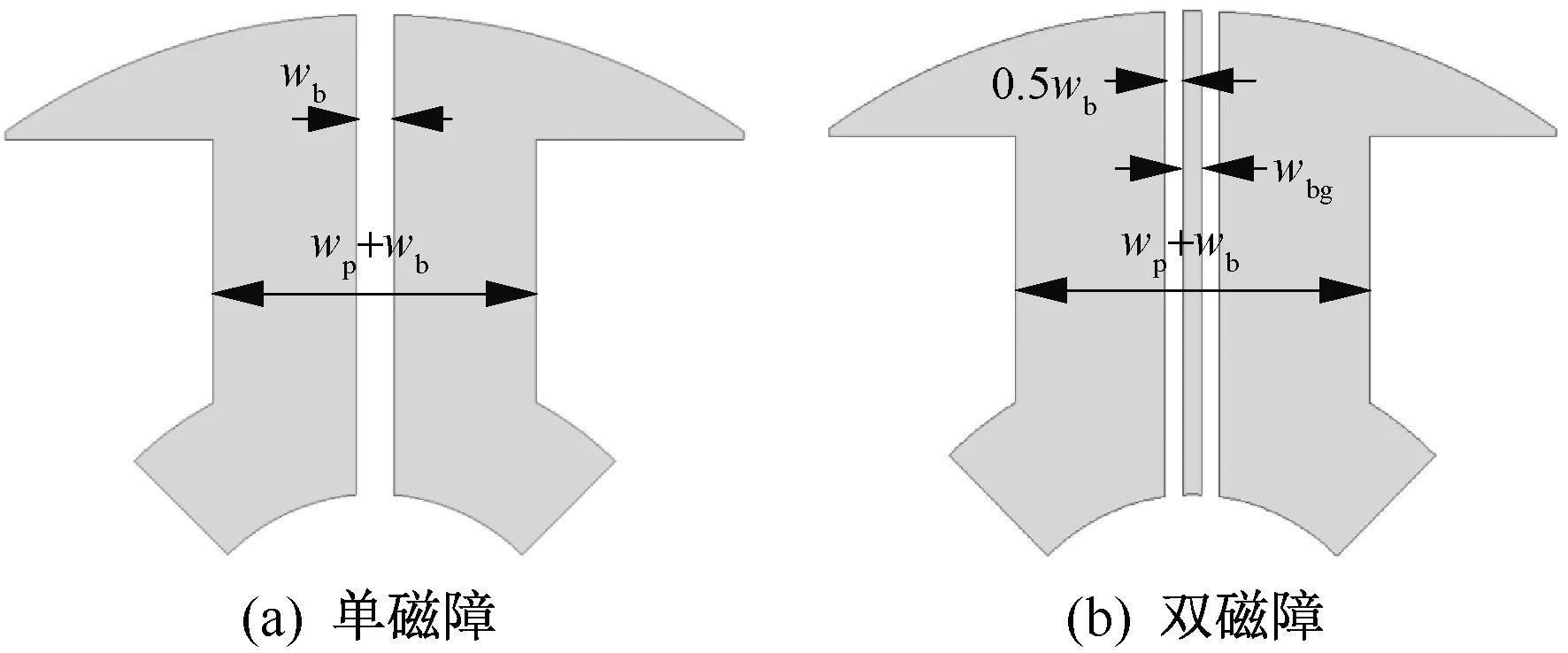
图6 转子极两侧增加宽度时的转子结构

以磁障宽度为参数进行有限元分析,如图7所示。单磁障宽度为5 mm，占转子极宽14.2%时，总转矩提升最多；双磁障宽度为3 mm，占转子极宽的8.5%时总转矩提升最多。

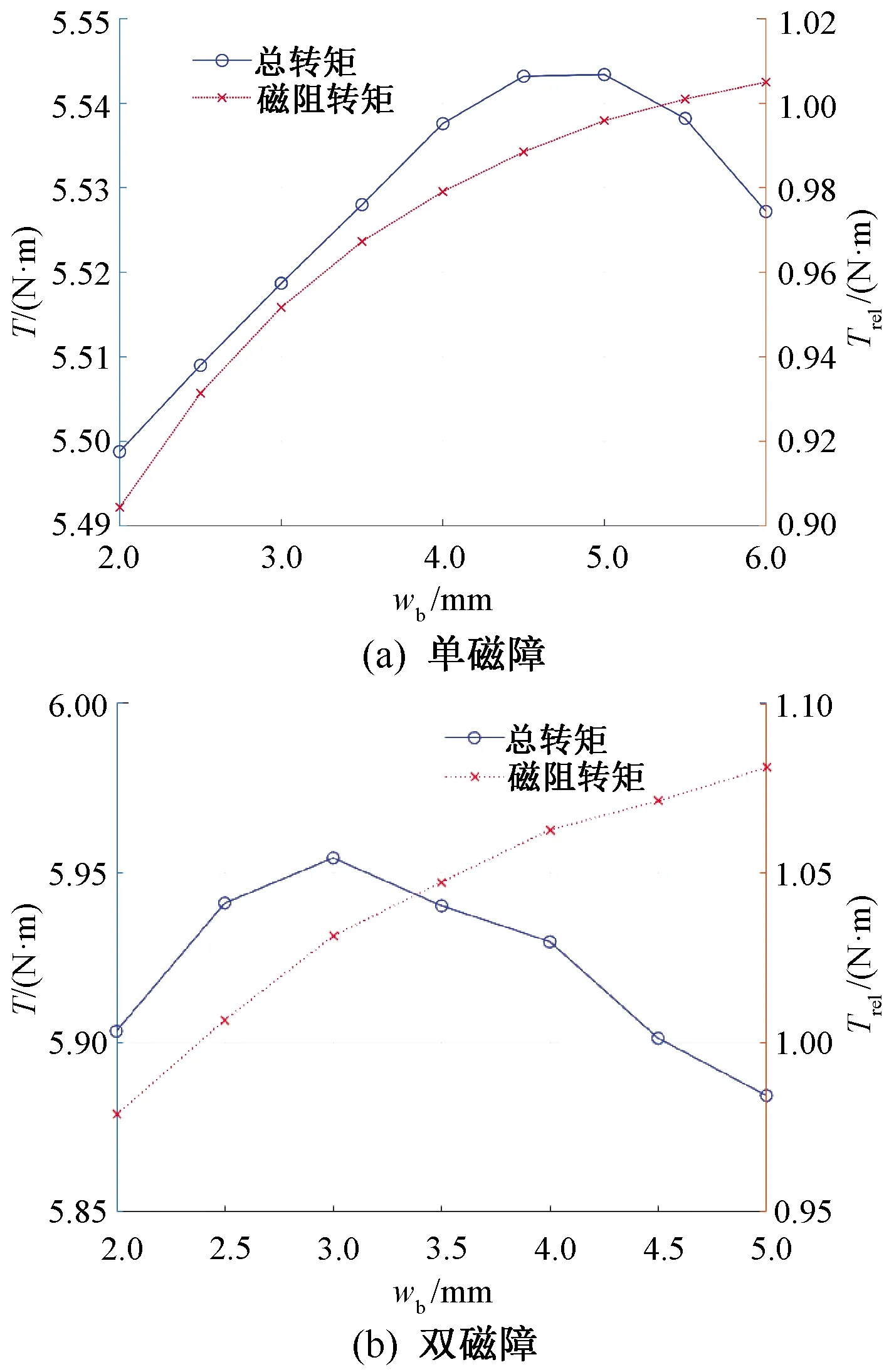
图7 转子极两侧加极宽时的总转矩、磁阻转矩变化情况

2.3d轴磁路导磁面积不变(不对称转子)时的磁障设计

为了分析在d轴磁路导磁面积不变的前提下不同转子结构对输出转矩的影响，本文在转子极一侧加转子极宽，转子结构如图8所示。图9为在转子极一侧加极宽时总转矩和磁阻转矩的变化情况。

图8 转子极一侧增加宽度时的转子结构

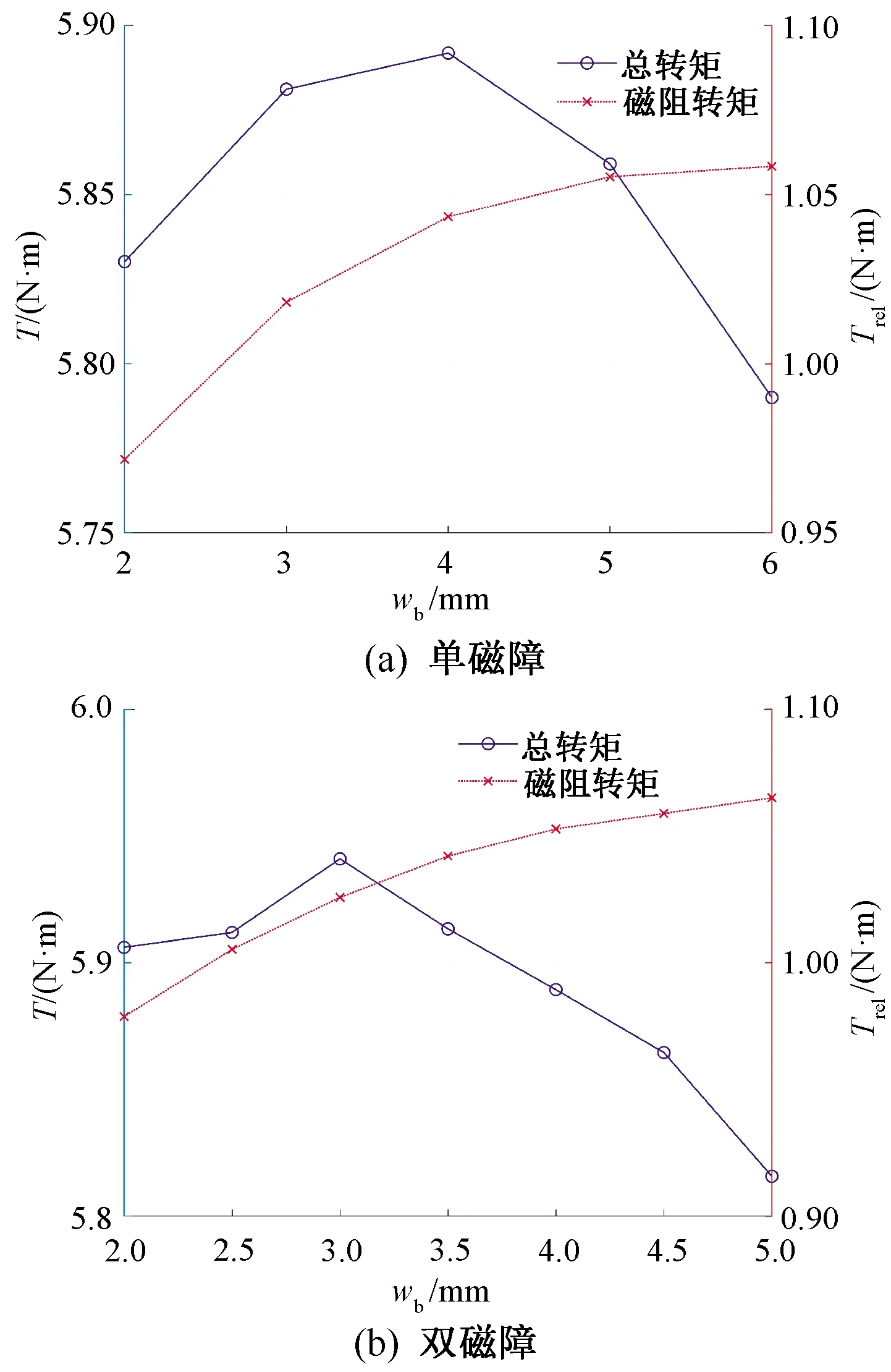
图9 转子极一侧加极宽总转矩、磁阻转矩变化情况

仿真结果表明，单磁障宽度为4 mm，占转子极宽11.4%时，总转矩提升最多；双磁障宽度为3 mm，占转子极宽8.5%时总转矩提升最多。

各类最优情况对应的总转矩和磁阻转矩如图10所示。图10表明,在d轴磁路导磁面积不变(对称转子)的前提下设置双磁障，总转矩提升最多；并且和传统电励磁电机相比，总转矩提升13.9%。

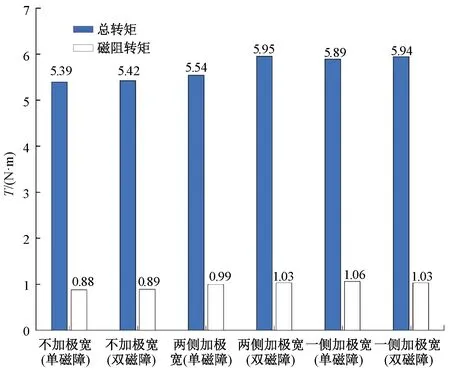
图10 各类最优情况下的总转矩和磁阻转矩对比

3 磁偏置原理及仿真分析

为了在设置磁障的基础上提升磁阻转矩的利用率，本文在磁障内放入永磁体，通过调整永磁体的充磁方向和q轴磁力线方向相反实现磁偏置，减小励磁转矩和磁阻转矩达到最大值时的电流角差，从而在设置磁障的基础上提升总转矩输出。

3.1 磁偏置原理

图11对加入永磁体后的WFSMFB各部分励磁单独分析。图11(a)为只有励磁线圈激励时的简化转子结构,dwinding表示为转子磁力线中心线方向，而凸极电机转子结构本身存在r-s轴来体现其具有的凸极效应[11]，r轴对应于磁阻最小的磁路方向，定义为dr，s轴对应磁阻最大的磁路方向，定义为ds。当转子侧只有励磁线圈激励时，转子磁链的相量方向和dr方向相同。当转子侧只有永磁体作用时，转子磁链的相量方向和dwinding方向相差90°电角度，定义为dPM，如图11(b)所示。当励磁电流和永磁体同时作用时，转子磁链的相量方向在dwinding和dPM之间，将其定义为df，如图11(c)所示。

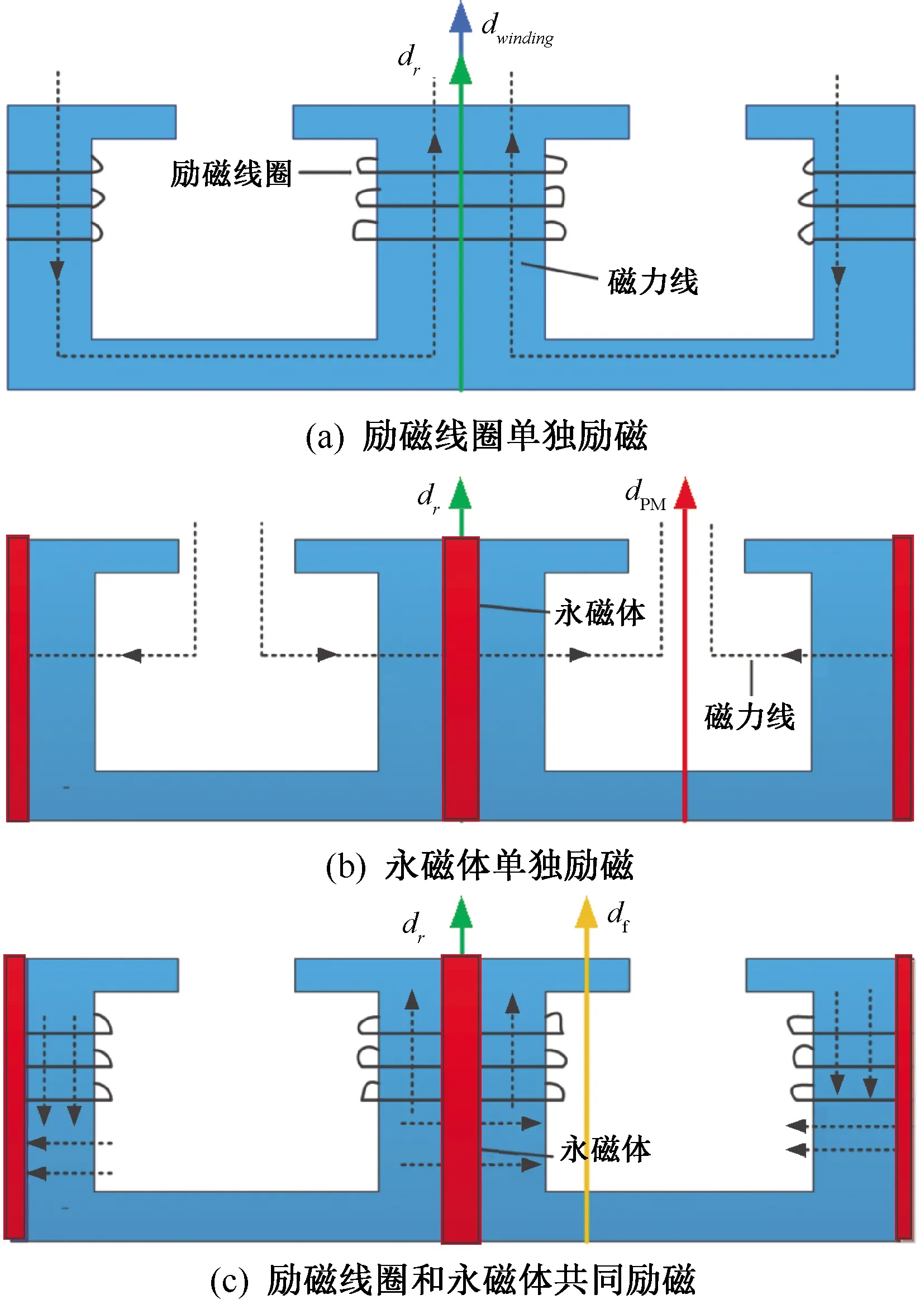
图11 加入永磁体后WFSMFB的各部分励磁

图12更直观地表现WFSMFB和在WFSMFB的磁障内放入永磁体后的d，q轴变化情况。在磁障内放入永磁体后q轴和ds轴之间存在一个电角度差δ,体现在转矩变化方面则是励磁转矩和磁阻转矩轴线之间的电角度差减小了δ,则磁偏置后的最大转矩相比于之前有所提升，如图13所示。

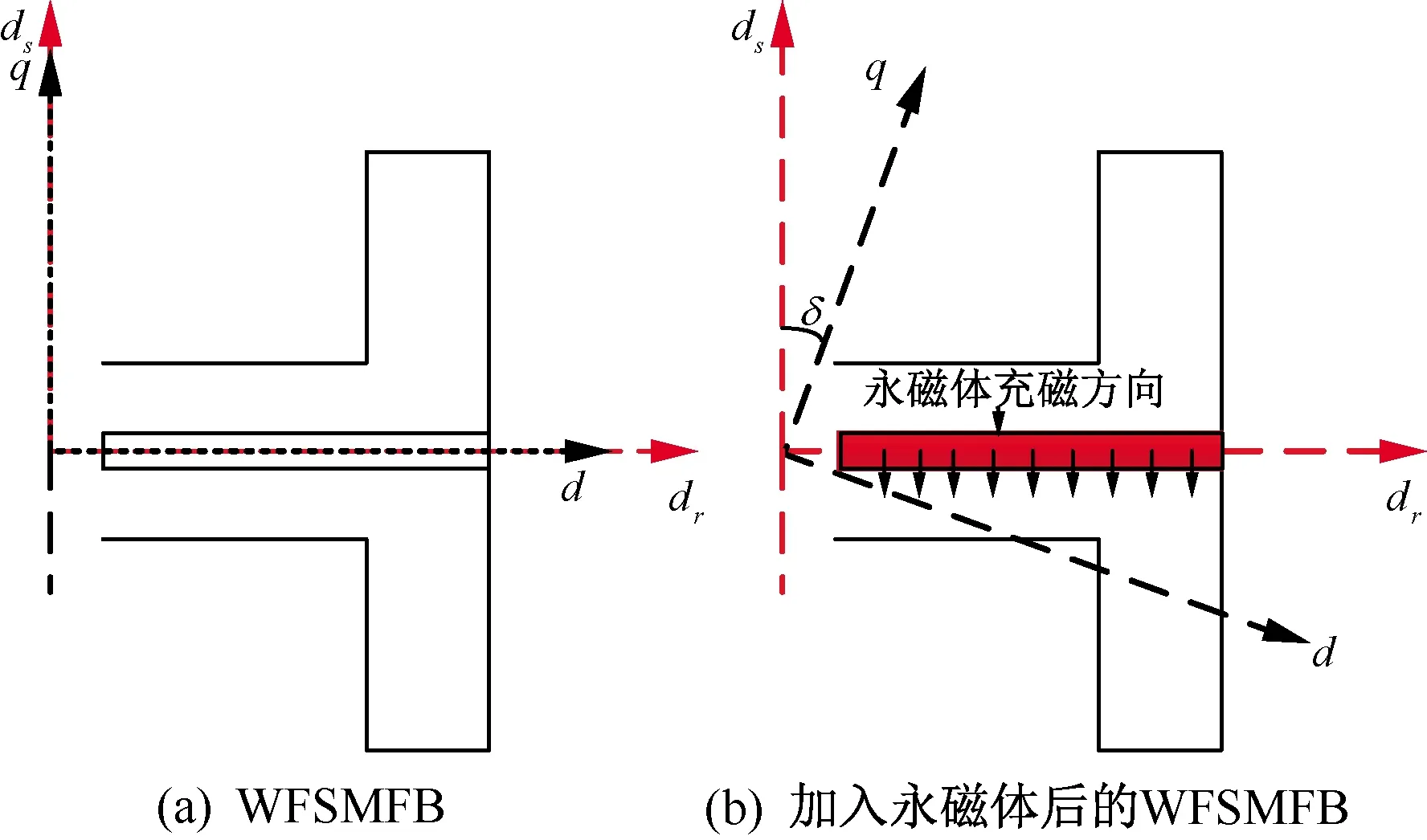
图12 d，q轴系统

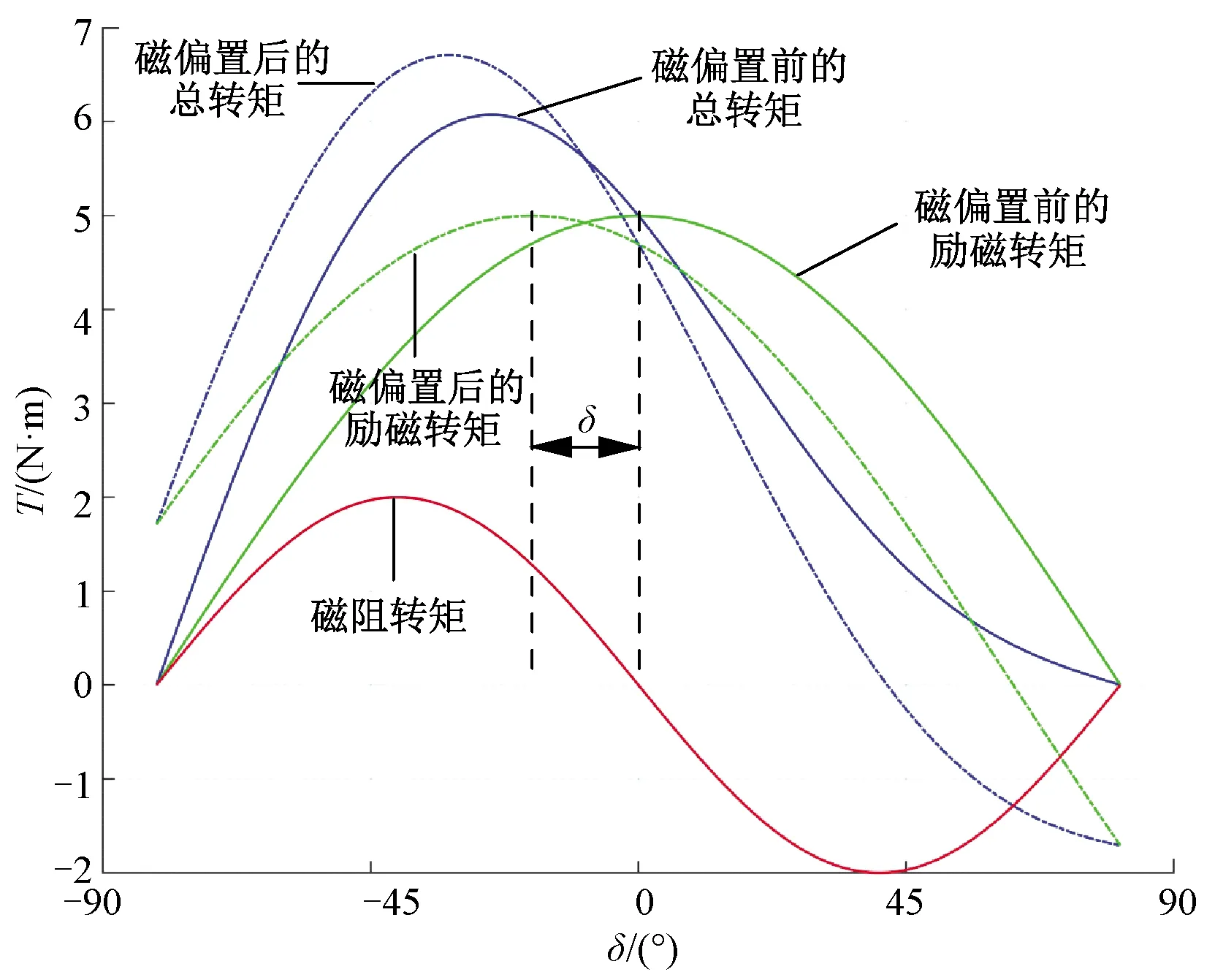
图13 磁偏置前后转矩对比图

3.2 磁偏置仿真分析

对d轴磁路导磁面积不变(转子对称)前提下的双磁障模型进行磁偏置仿真分析，如图14所示。永磁体材料选为铁氧体，永磁体宽度即为磁障宽度，利用有限元分析永磁体长度对输出转矩的影响。结果表明，当永磁体长度为40 mm时，平均转矩输出达到峰值。

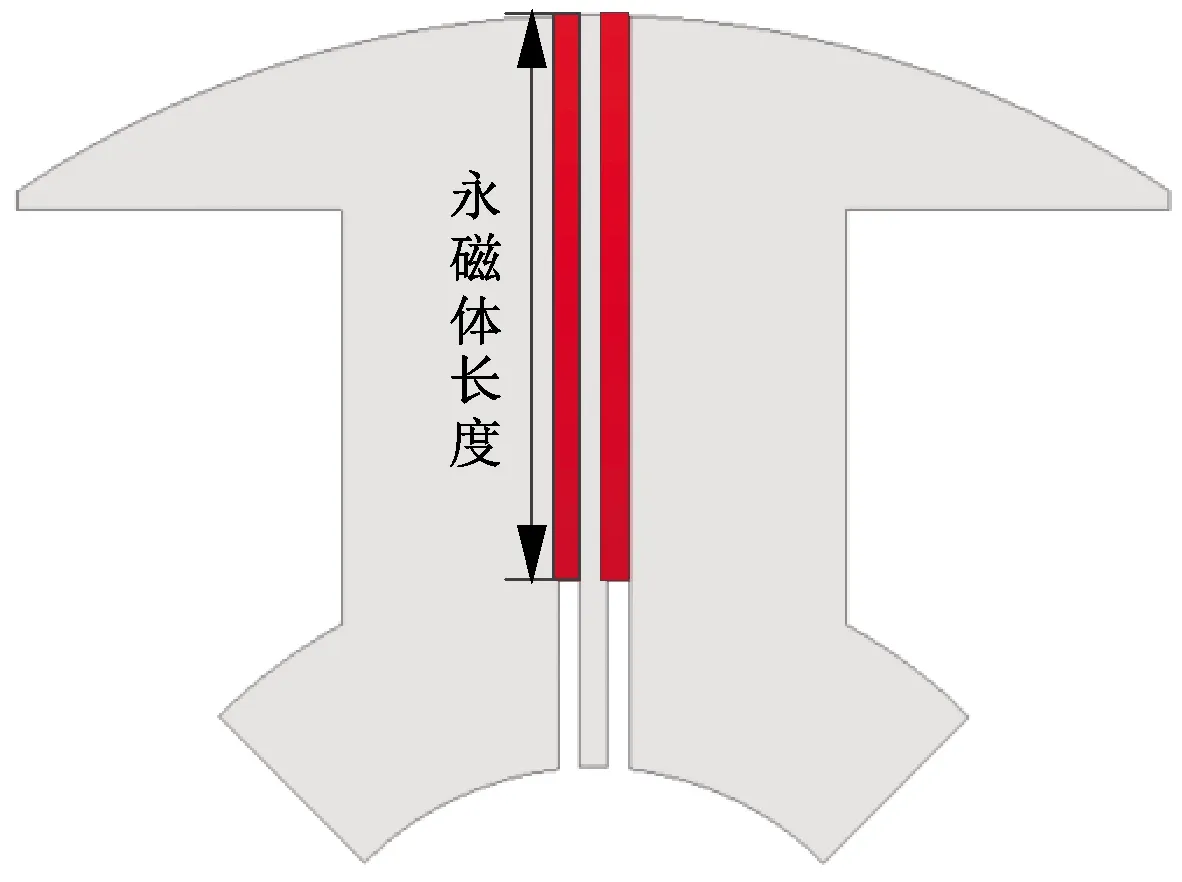
图14 磁障内加入永磁体后的WFSMFB转子结构图

定义磁阻转矩的利用率：

(9)

式中：Trel为最大输出转矩对应的磁阻转矩；Trelmax为磁阻转矩最大值。图15对比在磁障内加永磁体前后各部分转矩随电流角的变化情况，磁障内设置永磁体一方面能提升励磁转矩输出，另一方面也能提升磁阻转矩的利用率。

图15 转矩特性

表2将传统WFSM、WFSMFB、在磁障内放入永磁体的WFSMFB(简称加PM)三种电机模型的电磁特性进行对比。WFSMFB的总转矩相比于传统WFSM提升13.9%，原因在于磁障的设置带来了磁阻转矩的提升；在WFSMFB的磁障内加永磁体后，由于有永磁体充当励磁源以及磁偏置技术的利用，总转矩在设置磁障的基础上提升了14.5%。

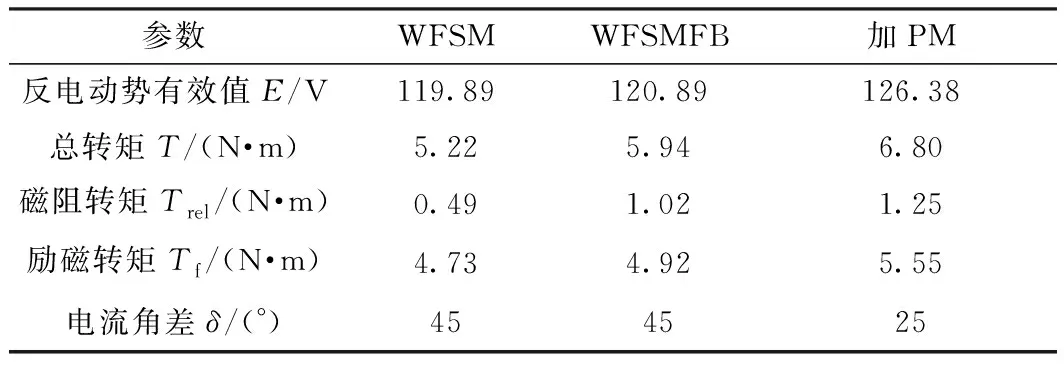
表2 三种电机模型结构的电磁性能对比

4 结 语

本文在传统电励磁电机的转子侧设置磁障提升磁阻转矩，并且在磁障内设置永磁体实现磁偏置，使励磁转矩和磁阻转矩最大值对应的电流角差从45°减小为20°，提升了磁阻转矩的利用率。有限元分析表明，在d轴磁路导磁面积不变(转子极对称)的情况下设置双磁障时总转矩提升最多，相比于传统电励磁电机提升13.9%。此时，磁障的总宽度为3 mm(占转子极宽8.5%)，磁障之间的距离为2 mm(占转子极宽5.7%)。在磁障内加入永磁体后，由于永磁体充当励磁源以及磁偏置技术的利用，总转矩在设置磁障的基础上提升14.5%。