Mavpd混沌系统的比例积分滑模同步控制
2021-11-16王东晓毛北行
王东晓,毛北行
(郑州航空工业管理学院 理学院,河南 郑州 450046)
最近20年来,混沌系统的滑模同步问题日益成为研究热点[1-12],孙宁,等(2010)[13]研究了一类不确定混沌系统的滑模投影同步问题,实现了主从系统的滑模投影同步.余名哲,张友安(2014)[14]研究了不确定混沌系统的滑模适应同步问题,能够使驱动-响应系统达到快速同步.仲启龙,等(2015)[15]研究了一类分数阶混沌系统的滑模同步问题,张燕兰(2014)[16]研究了分数阶Rayleigh-Duffling-like系统的追踪投影同步.文献[17]研究了一类不确定系统的滑模终端控制问题.文献[18]研究了一个新混沌系统的滑模控制问题,利用比例积分滑模方法研究了该系统的稳定性.文献[19]研究了比例积分追踪制导方法,为了保证追踪误差稳态值维持在较小的范围,采用了比例积分控制.而Mavpd混沌系统包含丰富的密匙参数,因此引起了控制界的广泛关注,例如:文献[20]研究了一类具有二次项的Mavpd混沌系统的动力学分析问题,讨论了该系统的平衡点,特征值和Lyapunov指数.本文在上述研究的基础上,研究了Mavpd混沌系统的比例积分滑模同步问题,基于比例积分滑模控制研究方法设计了滑模面和控制器,给出了系统取得同步的充分性条件.研究结果表明:选取适当的控制器与滑模函数,Mavpd系统的误差稳态值能够维持在较小的范围内.
1 主要结果
Mavpd系统如下[20]

(1)
当参数取值λ=100,μ=0.1,γ=1.6,β=200时,系统(1)呈混沌态.以该系统为主系统,设计从系统为

(2)
定义系统误差e1=x2-x1,e2=y2-y1,e3=z2-z1,两式相减得误差系统为

(3)
滑模控制的基本思想是选取适当的滑模函数和控制器,使系统的状态轨迹能够在有限时间内达到滑模面,并沿滑模面运动到指定状态,选取比例积分滑模函数

(4)
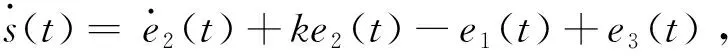

(5)
为使误差系统的状态轨迹能够在有限时间内达到滑模面,选取控制器,其中η为大于零的常数.
u(t)=-(k-γ)e2(t)-ηsgn(s(t))
(6)
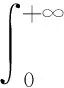
假设1|e1-e3| 所以s(t)可积且有界,根据引理1可知,因此不在滑模面上的点被驱动到滑膜面上. 由 再由假设2有,|x1x2|- 很容易得到s→0,e1→0,e2→0时e3→0,从而定理得证. 以下考虑整数阶Mavpd系统为主系统,亦可以实现积分滑模同步. (7) 从系统为 (8) (9) 假设3Δf(y)+d(t)=g(t), |g(t)|<ρ<η. 假设4|g(t)|<δ|e2|. 所以s(t)可积且有界,根据引理1可知s(t)→0,将等效控制器带入式(3)得到理想滑模方程 (10) 根据假设1,4得到 当M+δ 为了说明该方法的有效性,无妨利用MATLAB,采用预估校正算法进行数值仿真,系统参数取值λ=100,μ=0.1,γ=1.6,β=200,k=3,η=2,δ=1.5,M=1.2,ρ=1.5,N=0.5,主从系统初始值设置为(x1(0),y1(0),z1(0))=(2,1,3), (x2(0),y2(0),z2(0))=(1,2,2),不确定项Δf(x2,y2,z2)=0.2sin(x2y2z2),外扰d(t)=0.02/(1+5t),定理1,2中的系统误差曲线如图1,2所示,从图中可以看出,初始时刻系统误差曲线相距甚远,随时间推移,系统误差曲线在有限时间内趋于原点,且渐趋一致. 图1 定理1中的系统误差曲线Figure 1 The system errors of theorem 1 图2 定理2中的系统误差曲线Figure 2 The system errors of theorem 2 基于比例积分滑模控制研究方法研究了Mavpd混沌系统的滑模同步问题,设计了滑模面和控制器,给出了系统取得同步的充分性条件,并给出了严格的数学推理和证明过程,研究表明:选取适当的控制器与滑模函数,Mavpd系统的主从系统取得积分滑模同步.最后数值算例验证了该方法的可行性与有效性.












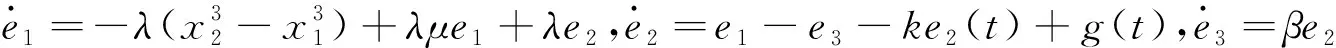

2 数值仿真


3 结 论
