状态调控下的脉冲多智能体系统一致性分析

王蒙蒙，李智勇，宾红华

(集美大学 理学院，福建 厦门 361021)

近年来，多智能体系统因其在信息融合[1]、传感器网络[2]、编队控制[3]等领域的广泛应用受到了众多研究者的关注.一致性作为多智能体系统中的核心问题已被广泛研究[4-6].到目前为止，有以下几种不连续的控制方案被应用于神经网络和多智能体网络:自适应控制[7]，量化控制[8]，脉冲控制[9-10]等.

近来，脉冲控制的多智能体系统一致性问题已有大量成果[11-13].同时，有许多学者已经研究了脉冲序列非状态依赖下的多智能体系统一致性问题.例如，文献[11]利用一种新型的脉冲控制策略研究了多智能体网络系统的一致性.文献[12]研究具有固定拓扑和切换拓扑的二阶多智能体系统的一致性.文献[13]研究脉冲多智能体系统，设计了基于牵制单个节点的控制策略，给出了一致性准则.同时，近年来也有学者研究了基于脉冲序列依赖状态或脉冲控制器中纳入时滞项下的动态网络系统的同步.例如，文献[14]通过牵制脉冲策略，研究了一种具有非线性耦合的随机动态网络，给出了随机网络的稳定性标准.文献[15]利用时滞脉冲牵制控制，研究了线性动态网络在时标上的同步.

然而，目前研究多智能体脉冲控制一致性问题时，脉冲序列依赖状态或者由状态来决定的研究较为少见，但是依状态来确定脉冲序列对探索多智能体的脉冲控制效果和收敛速度是一个极其重要的研究课题.与此同时，脉冲控制器中存在时滞的情况也引起学者的重视[15].受文献[14-15]的启发，结合文献[3]，本文研究基于状态调控下的时滞脉冲多智能体一致性问题，得到多智能体网络系统达到一致性的充分条件.其结果是对已有文献的推广与补充.

1 系统模型及预备知识

1.1 具有延迟性脉冲控制的多智能体网络系统

考虑以下多智能体网络系统

(1)

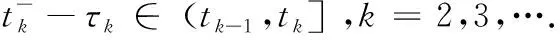
(2)

(3)

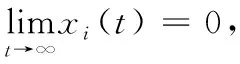
1.2 相关定义、引理及图论知识

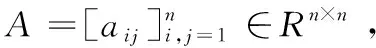
2)除了一个重数为1的特征值0，A的特征根的实部都是负数.则称A∈A1.

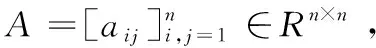
2)A是不可约的.则称A∈A2.显然A2⊆A1，同时可得以下引理.

引理1[13]若A∈A1，则以下项成立:

2)A∈A2当且仅当ξi>0对所有i=1,…,n都成立.

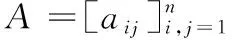
注2由引理1可知，对-L∈A2，令Ξ=diag[ξ1,…,ξn]是由-L对应于特征值0的左特征向量生成的对角矩阵，则-(ΞL+LTΞ)∈A2对称，其中ι>0是对角矩阵ΞL+LTΞ的最小特征值.

2 主要结论

为了得到本文主要结果，我们首先对以下引理进行证明.

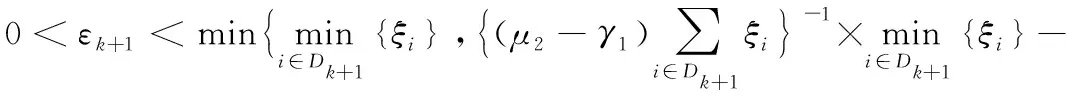
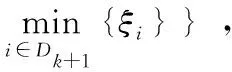
成立，x(t)是系统(1)的一个解.基于状态调控的脉冲策略，定义脉冲列{tk}满足:

(4)

则有

(5)

和

(6)

其中k=0,1,2,….

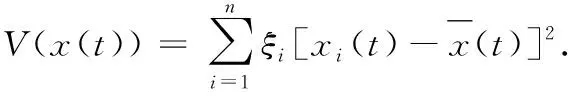
故有

(7)

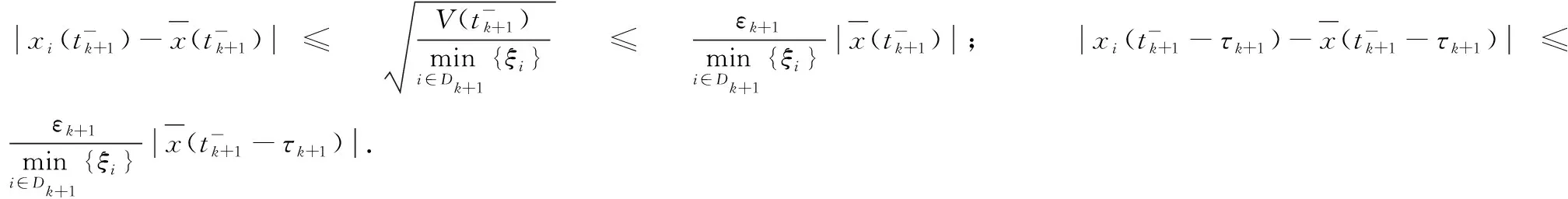
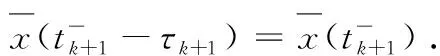
(8)

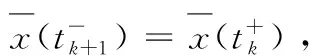
(9)

从而式(5)成立.另一方面，由

和式(7)，可得

(10)

(11)

(12)

故有

(13)

即式(6)得证.

注3目前大部分脉冲控制的多智能体一致性的研究都是基于给定脉冲序列，没有考虑状态或由状态来决定调控的脉冲[11-13]，由状态来调控脉冲的脉冲序列不仅影响脉冲调控的时间，而且会决定调控的效果和收敛速度.因此，本文考虑的这个脉冲调控不仅考虑状态影响，而且也考虑了时滞影响.

注4状态脉冲调控策略(4)是对每个脉冲点都要进行估计且状态脉冲调控策略是依赖于前一个脉冲点的状态.因此，如果我们根据初始状态可以计算出每两个脉冲点之间最小的调控区间，这在实际的脉冲控制上不仅可以节约计算成本并且提高了计算效率.

从引理2，可以由状态估计最小的脉冲控制区间，从而我们可以得到以下推论.

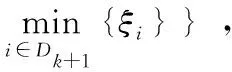
(14)

(15)

则对每个k，基于状态的脉冲调整策略式(4)满足Δtk≥Tk+1时有

(16)

下面给出本文的主要结果.

定理1若-L∈Α2，则对每个k,α1k∈[μ1,μ2],α2k∈[γ1,γ2]，且满足

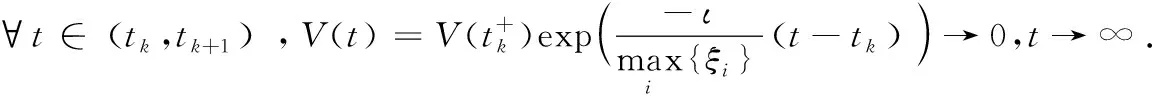
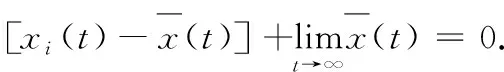
注5本文吸收了文献[14-15]对误差进行排序思想，提出了基于状态的脉冲调控策略，该策略不仅考虑了误差的排序并且考虑了时滞，是对已有文献的推广[13-15].

注6通过引入Dk，给出了新的牵制控制方案，当Numb(Dk)=n,α2k=0时，我们的结果推广和改进了文献[16].而如何来确定牵制多智能体的个数lk与脉冲调控序列的关系有待今后进一步研究.

3 数值模拟

对多智能体系统(1)，考虑拉普拉斯矩阵为

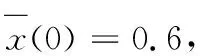
由于在脉冲时刻控制节点和节点个数不同，故(a)，(b)，(c)三种情形计算脉冲序列{tk}都需对脉冲时刻分类讨论.

情形(a)，由于在脉冲时刻没有添加控制器，故网络(1)的轨迹与脉冲时间间隔无关.

情形(b)，取γ1=γ2=0.(1)偶数时刻，取μ1=μ2=0.4,ε2k=0.1249,∀k∈N，则C2k==109.8753,T2k=26.9777.(2)奇数时刻，取μ1=μ2=0.55,ε2k-1=0.1249,∀k∈N，则当控制节点x1,x2,x3时，C2k=5126.1,T2k=23.4818.当控制节点x1,x2,x4时，C2k-1=5126.1,T2k-1=23.4818.当控制节点x1,x3,x4时，C2k-1=214.7366,T2k-1=16.4687.当控制节点x2,x3,x4时，C2k-1=25.1045,T2k-1=5.8622.

情形(c)，(1)偶数时刻，μ1=μ2=0.4,γ1=γ2=0.2,ε2k=0.1249,∀k∈N，那么C2k=136.8802,T2k=16.4734.(2)奇数时刻，μ1=μ2=0.55,γ1=γ2=0.25,ε2k-1=0.1249,∀k∈N.那么当控制节点x1,x2,x3时，C2k-1=55.3169,T2k-1=14.4706.当控制节点x1,x2,x4时，C2k-1=55.3169,T2k-1=14.4706.当控制节点x1,x3,x4时，C2k-1=198.7889,T2k-1=17.2982.当控制节点x2,x3,x4时，C2k-1=151.7249,T2k-1=8.8505.

数值模拟中取Δtk≥29.图1-3分别为(a)，(b)，(c)三种情况的仿真结果.由图1可以看出，为了使系统对某个值达到一致性，必须要对系统进行控制，即对每个k,α1k>0.再由图2，图3可以看出，脉冲控制器中时滞项的存在可使系统更快的达到一致性.

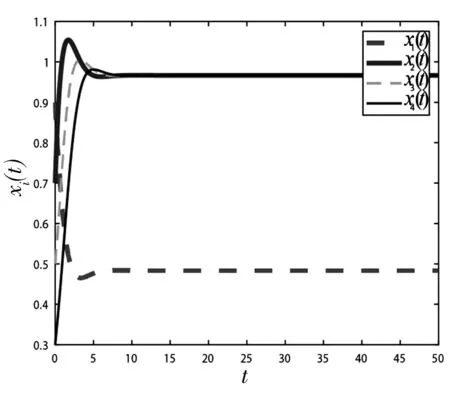
图1 系统(1)不添加控制器Figure 1 System (1) does not add Controller

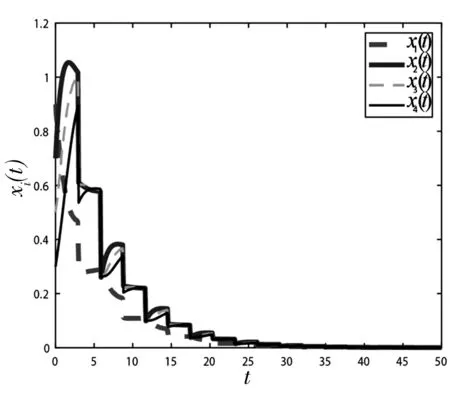
图2 系统(1)添加脉冲控制器Figure 2 System (1) add impulse Controller

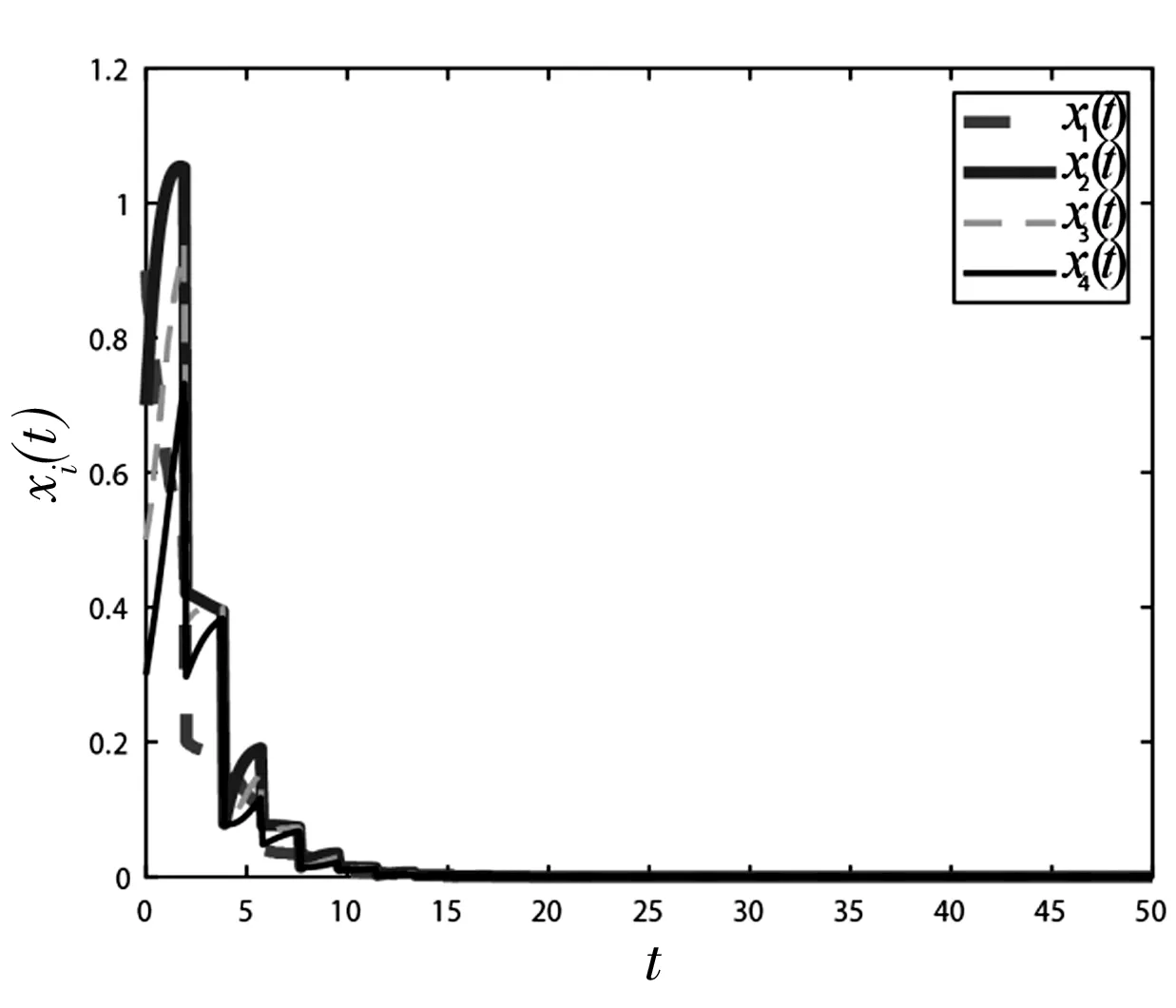
图3 系统(1)添加时滞脉冲控制器Figure 3 System (1) add time-delay impulse controller

4 小 结

本文通过提出基于状态的脉冲调控策略，给出了多智能体系统一致性标准，所得结果不仅推广了非状态依赖脉冲控制和误差排序牵制控制的已有结果，同时也提供了依赖时滞和状态调控的一致性新方法.数值模拟结果表明，控制方案有效，且时滞可以加快速度.