基于改进Hanning窗函数电力系统间谐波检测高精度简明算法
2021-11-16王震,陈卓
王 震, 陈 卓
(贵州大学 电气工程学院,贵州 贵阳 550025)
随着新能源战略的推进,大量风机、太阳能设备、电动汽车充电桩等投入运行。这些设备都采用了大功率电子电力变流器件,在它们运行使用过程中会产生大量间谐波。间谐波的产生,降低了电网电能质量,严重威胁着同电网下的用电设备安全,间谐波检测问题逐渐引起人们关注。
间谐波比谐波更容易受到频谱泄露的影响,因此对算法检测的精度要求更高,早期所研究的谐波检测算法无法满足间谐波检测要求。为了提高检测精度,许多专家、青年学者对传统谐波检测算法提出了改进方案,根据加窗函数不同和利用谱线的数量可分为四项窗双谱线插值算法[1]、五项窗三谱线插值算法[2]、六项窗六谱线插值算法[3]等。虽然多项窗函数可以很好地抑制频谱泄露,但是由于窗函数过于复杂,插值公式根本无法推导。为此,文献 [1,3-4]通过多项式拟合函polyfit进行拟合,文献 [2]采用MATLAB中的cftool工具进行函数逼近,文献 [5]则利用切比雪夫多项式进行函数逼近。拟合公式一方面计算量较大,另一方面拟合公式的残差也会限制检测结果的精度。一个好的算法应当尽可能简洁、精确,本文基于改进Hanning窗函数,构造一种具有简明插值公式的高精度插值算法,避免了采用拟合公式插值法的残差问题,同时因其简洁而节约了计算量。
1 改进Hanning窗函数插值算法
做谐波、间谐波检测时,需要考虑频谱泄露和栅栏效应两个问题。抑制频谱泄露的主要是加窗函数,针对栅栏效应则需要做插值计算。窗函数的优劣及插值公式准确性两者共同决定了检测结果的精度。
1.1 加窗插值算法基本原理及问题

图1 单信号频谱图Fig.1 Spectrum of single frequency signal
加窗插值算法基本流程:
首先,对于原始信号进行采样得到序列x(n),
x(n)=Acos (2πf0nTs+φ),
(1)
其中:n=0,1,2,…,N-1;Ts为采样时间。
然后,对采样序列x(n)加窗函数w(n),并做频谱变换:
(2)
频谱图如图1所示。由于加了窗函数,f0在其他频率附近的谱线得到抑制。
再利用待测频率f0附近谱线X(K)、X(K+1)的频谱值,引入参数U,
(3)
最后得到插值结果ΔK。
加二项窗Hanning窗时
(4)
其中n=0,1,2,…,N-1。准确的Hanning窗表达式余弦项分母为N-1,但实际做插值计算时表达式中分母为N要优于N-1,本文采样分母为N。
插值公式为[6]
(5)
加三项窗Blackman窗时
(6)
利用polyfit拟合到插值公式为
ΔK=-1.692 001+5.473 062U-8.768 038U2+12.879 910U3-
14.036 202U4+10.079 386U5-4.204 462U6+0.768 347U7,
(7)
加Hanning窗函数时插值公式简约明了,但Hanning窗函数抑制频谱泄露效果不如Blackman窗函数。Blackman窗函数虽然抑制频谱泄露效果好,但插值公式只能通过拟合得出,而拟合函数的精确度也会限制算法的精度。其他窗函数如四项Nutall窗、五项MSD窗同样也面临插值公式无法导出问题,拟合得到的插值公式不但表达式复杂,而且会因为残差问题算法精度受限。
1.2 改进Hanning窗插值算法
因为Hanning窗插值算法有准确的插值公式,因此可以对Hanning窗进行改进得到更高数项的窗函数,同时还可以导出插值公式。
矩形窗(不加窗函数)的频域函数为
(8)
WR(k)幅值连续图像如图2所示,可以看出其幅值图像成起伏式衰减。
加Hanning窗函数,物理意义是原频谱减去频谱左右平移的平均值,即
W(k)=WR(k)-0.5(WR(k+1)+WR(k-1))。
(9)
加Hanning窗连续频谱图像如图3所示。可以看出,加窗后频谱图能量向中间集中,两侧频谱泄露得到抑制,但仍然成起伏式衰减。因此可以二次加Hanning窗,实现进一步频谱泄露抑制。
对Hanning进行乘方运算
w2(n)=w(n)·w(n)。
(10)
得到一个新的窗函数
(11)
其中n=0,1,2,…,N-1,该窗函数是一种三项余弦组合窗函数。

图2 不加窗连续频谱图 图3 Hanning窗连续频谱图Fig.2 Continuous spectrum of rectangular window Fig.3 Continuous spectrum of Hanning window

图4 频谱特性图Fig.4 Spectral characteristic of window function
频谱特性图(图4)对比如下:
对比窗函数频谱特性图,可以看出:改进 Hanning 窗最大旁瓣比原Hanning窗小,且衰减快; 同样是三项窗函数,改进Hanning窗函数的衰减明显比Blackman 窗函数快,虽然Blackman窗函数最大旁瓣要比改进Hanning窗函数小,但在用于间谐波检测时并不具有优势。另外,主瓣变宽会影响频谱分辨率。m值不宜过大,应保证各次波不在彼此主瓣宽度内,避免影响各次波检测计算。
根据式(8)、式(9)可以得到x(n)加二次Hanning频谱表达式近似为

sin ((k-K0)π) ejφe-j(k-K0)π,
(12)
取-ΔK=K-K0,则
(13)
二次Hanning窗插值公式为
(14)
插值公式简单明了。Blackman窗函数插值拟合公式法需要进行21次乘法运算,而本文插值公式只需要一次乘法和一次除法,计算量明显比拟合公式小,且较拟合算法准确。
求得待测频率为
f0=(K+ΔK)fp,
(15)
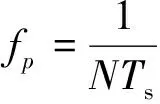
(16)
相位为φ=angle [X(K)]-ΔKπ。
(17)
通过归纳总结,可以得出m次Hanning窗函数
(18)
其插值公式为
(19)
即使是m次Hanning窗函数,插值公式计算量仍不变,计算量较小。
幅值公式
(20)
其中m=1,2,3,…m越大,频谱泄露抑制效果越好,但并不代表间谐波检测效果会越好,由于离散形式的频谱变换并非准确的积分运算,因此谱值会存在一定的误差。另外由于测量仪器的测量精度、计算模块对数据处理的精度等问题也会限制检测的精度。因此要选取合理的m值,既要保证精度,又要避免计算量的浪费。
2 算例分析
采样时间Ts=0.001 s,采样个数N=400。信号各次波参量的设置见表1。

表1 仿真参数设置Tab.1 The data of the simulated signal
分别利用加Hanning窗、加Blackman窗、改进Hanning窗(m=2,3,4)做双谱线插值对信号的各次波的频率、幅值等参量进行检测,频率测算相对误差百分比见表2,幅值测算相对误差百分比见表3。

表2 频率检测误差Tab.2 The error of frequency calculation %

表3 幅值检测误差Tab.3 The error of frequency calculation %
由分析检测结果可知,频率的精度比幅值精度高,这是因为频率可以根据插值公式直接得出,而幅值需要换算,换算时误差被放大; 无论是频率或幅值,基波测算精度要比谐波好,谐波测算精度要比间谐波好,各次波的测算精度受其含量影响。
算法之间的比较: 三项窗函数Blackman窗插值算法要比两项窗函数Hanning窗插值算法好,这是由于Blackman窗抑制频谱泄露能力强; 作为同样是三项窗函数二次Hanning窗插值算法在测算基波参量时要比Blackman窗效果好,这是因为二次Hanning窗插值公式没有误差; 在测量谐波、间谐波时参量时,二次Hanning窗插值算法误差要比Blackman窗插值小一个数量级,这主要是因为二次Hanning窗抑制频谱泄露能力强; 改进Hanning窗函数之间比较,m越大效果越好。
3 结论
本文提出的改进Hanning窗函数,改进方法简单明了,抑制频谱泄露抑制能力强。基于改进Hanning 窗构造的插值算法具有明确的插值公式,相比传统采用拟合公式插值法,计算过程简便快捷,计算结果精度高。从算例分析可以看出,归纳出的m次Hanning窗函数通用插值公式,随着m的增加,各次谐波、间谐波检测精度大幅提高,展现出了算法的巨大潜力。本文主要对双谱线插值算法进行了讨论,三谱线、四谱线等多谱线插值算法有待进一步研究。