笛卡尔与费马解析几何思想路径之比较与启示

2021-11-16陈惠勇

内蒙古师范大学学报(自然科学汉文版) 2021年6期

李慧, 陈惠勇

(江西师范大学数学与统计学院,江西南昌330022)

著名数学史家、中国科学院数学与系统科学研究院李文林先生认为“数学史研究具有三重目的,一是历史的目的,即恢复历史的本来面目; 二是数学的目的,即古为今用,为现实的数学研究与自主创新提供历史借鉴; 三是教育的目的,即在数学教学中运用数学史,这在当前已成为一种国际现象”[1]。莱布尼茨(G.Leibniz,1646—1716)曾指出:“知道重大发明特别是那些绝非偶然的、经过深思熟虑而得到的重大发明的真正起源是很有益的。这不仅在于历史可以给每一个发明者以应有的评价,从而鼓舞其他人去争取同样的荣誉,而且还在于通过一些光辉的范例可以促进发现的艺术,揭示发现的方法。”[2]

由此可知,数学史研究(特别是基于数学教育倾向的数学史研究)不仅对于数学研究本身,而且对于数学教育亦具有不可或缺的教育价值和现实意义。本文探究笛卡尔与费马创立解析几何的思想路径,并比较其异同及其对数学教育的启示与借鉴。

1 笛卡尔与《几何学》

近代数学本质上可以称为变量数学,而变量数学的第一个里程碑是解析几何的发明。1637年,法国数学家、哲学家勒内·笛卡尔(René Descartes,1596—1650)出版了《更好地指导推理和寻求科学真理的方法论》一书,此书包括三个附录《几何学》《折光学》和《论陨石》,解析几何这一数学分支就诞生于《几何学》中。

《几何学》全书分三编,围绕初等几何的作图问题展开,第一编“仅使用直线和圆的作图问题”,笛卡尔引进了“单位线段”的概念,定义了线段的加、减、乘、除及开方运算,解决了仅使用直线和圆的作图问题等“普通几何”问题(即相应方程中的未知量最高幂次不超过2次); 第二编“曲线的性质”,笛卡尔进一步发展解析几何方法,论述如何推导出具体代数方程并据以研究曲线的各种性质; 第三编“立体及超立体问题的作图”,以当时流行的代数问题为主题,其中包括了著名的“笛卡尔符号法则”。

可以看出笛卡尔早已被几何与代数结合的巨大力量所吸引,但他的目的在于通过几何方法构造代数方程的解,进而寻找解决作图问题的统一方法,真正体现其解析几何思想的内容源自对一个古希腊几何问题——帕普斯四线问题的解决。

帕普斯问题叙述如下: 设在平面上给定四条直线AG、GH、EF和AD,求从某点C作四条直线CB、CQ、CR和CS分别与已知直线交于已知角,且满足关系CB·CR=CS·CQ的点C的轨迹(如图1所示)。

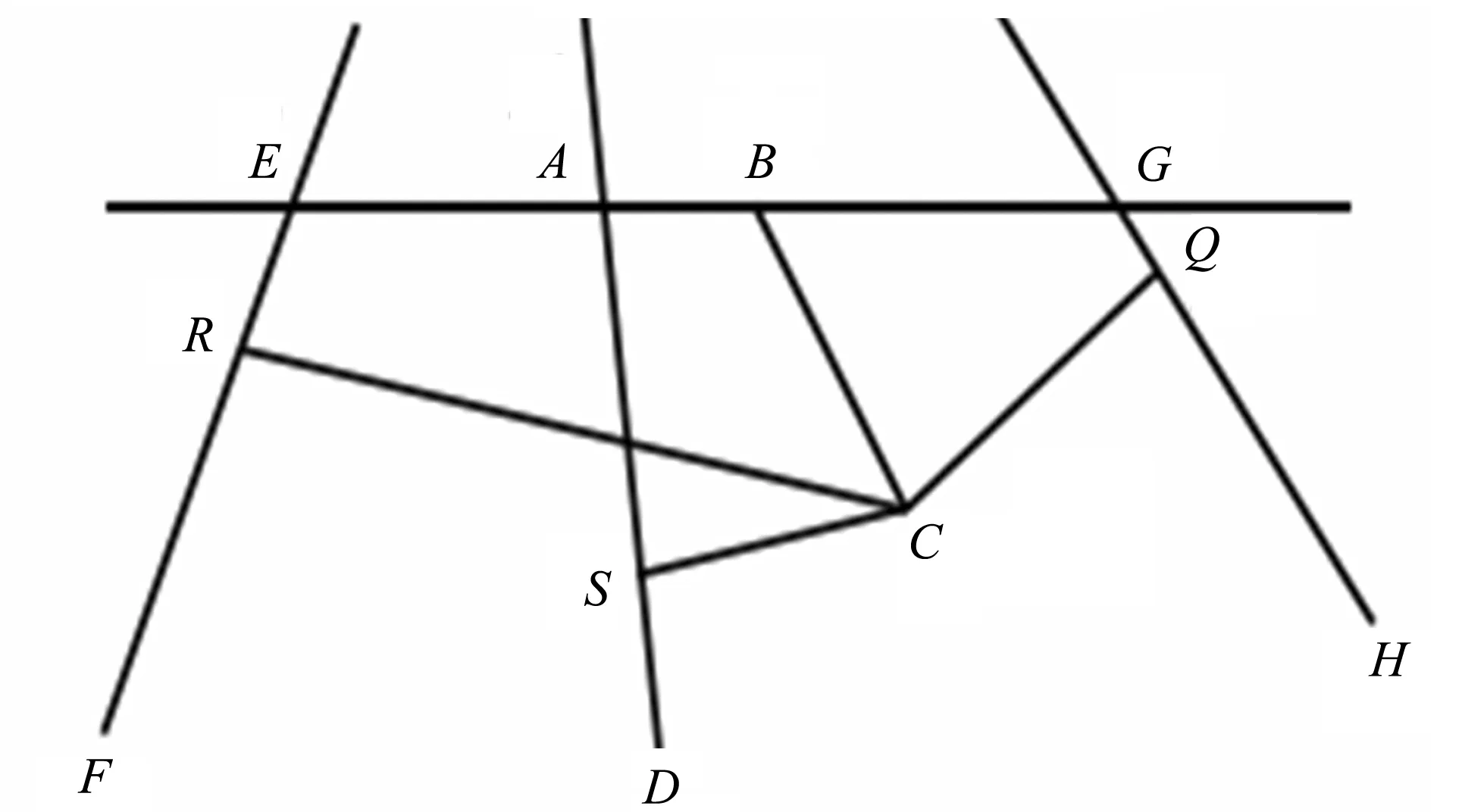
图1 帕普斯四线问题Fig.1 The problem of Pappus

笛卡尔首先阐明了解这类几何作图问题的一般原则:“于是,当要解决某一问题时,我们首先假定解已经得到,并给为了作出此解而似乎要用到的所有线段指定名称,不论它们是已知的还是未知的。然后,在不对已知和未知线段作区分的情况下,利用这些线段间最自然的关系,将难点化解,直至找到这样一种可能,即用两种方式表示同一个量。这将引出一个方程,因为这两个表达式之一的各项合在一起等于另一个的各项。”[3]

遵循这个原则,笛卡尔首先假设C点已找到,并将AB记为x,BC为y,然后根据已知条件和三角形的边角关系,分别将CR、CS及CQ用x和y表示出来,最后代入关系式CB·CR=CS·CQ中,整理后便得出了C点的轨迹方程(其中a、b、c、d是由已知量组成的简单代数式)

y2=ay+bxy+cx+dx2。

根据上述方程,对于任意给定的一个x,都可以立即找到一个y与之对应,线段BC的一个端点C随之画出一条曲线。由此,笛卡尔不仅成功寻找到了几何轨迹的代数方程,还使其几何代数化方法的可行性得以验证,点的“形”与方程的“数”统一起来,曲线与方程的概念也随之形成[4]。

尽管严格来说,笛卡尔根本没用到现代解析几何意义上的平面直角坐标系,而是以点B为坐标原点,AB间距离为x值,BC间距离为y值构造了一个斜角坐标系,但其中已经蕴含了解析几何的本质——用代数方程表示并研究几何曲线。

通过上述讨论,可以大致构造出笛卡尔解析几何思路为:几何作图问题(假设解已得到)→构造方程→方程求解。

在《几何学》一书末尾,笛卡尔给出了这样的结论:“对于复杂程度越来越高的问题,我们只要遵循同样的、具有普遍性的方法,就能完成其作图; 就数学的进步而言,只要给出前二三种情形的做法,其余的就很容易解决。”[3]这个结论表明,他设计的路线图旨在彻底解决几何作图问题,虽然低估了“遵循同样的方法”解决更高次方程的难度,但他创造性地把变量思想和坐标观念体现到了其几何代数化方法中,真正有意义地建立起代数与几何的本质联系,这也正是曲线与方程概念的雏形。笛卡尔的工作意义超出了他的最初预想,为后人提供了一个全新的思路,成为数学家们进一步研究的出发点。

2 费马与《平面与立体轨迹引论》

与笛卡尔不同,被称为“业余数学家之王”的皮埃尔·德·费马(Pierre de Fermat,1601—1665)是在试图恢复失传已久的阿波罗尼奥斯著作《论平面轨迹》的过程中发现了解析几何。费马的解析几何思想诞生于一篇仅有8页的重要论文——《平面与立体轨迹引论》,此文大约完成于1629年,但直到他去世后才在其子编辑的《数学论集》中发表出来。

在文中,费马用代数方法对阿波罗尼奥斯关于轨迹的一些失传的证明作了补充,对古希腊几何学,尤其是阿波罗尼奥斯的圆锥曲线论进行了整理和总结,对曲线作了一般研究。

笛卡尔大胆采用独具创造性的方法,从曲线轨迹出发寻找其方程。而费马则致力于完善阿波罗尼奥斯的工作,继承了希腊人的思想,即从方程出发寻找它的轨迹,其重点在于不定方程解法的图示。

费马在论文中这样描述其解析几何思想的基本原理:“每当在最后的方程中出现了两个未知量,我们就得到一个轨迹,其中一个未知量的端点描绘出一条直线或曲线。这条直线简单且唯一,曲线的种类无限多——圆、抛物线、双曲线、椭圆等。”[5]

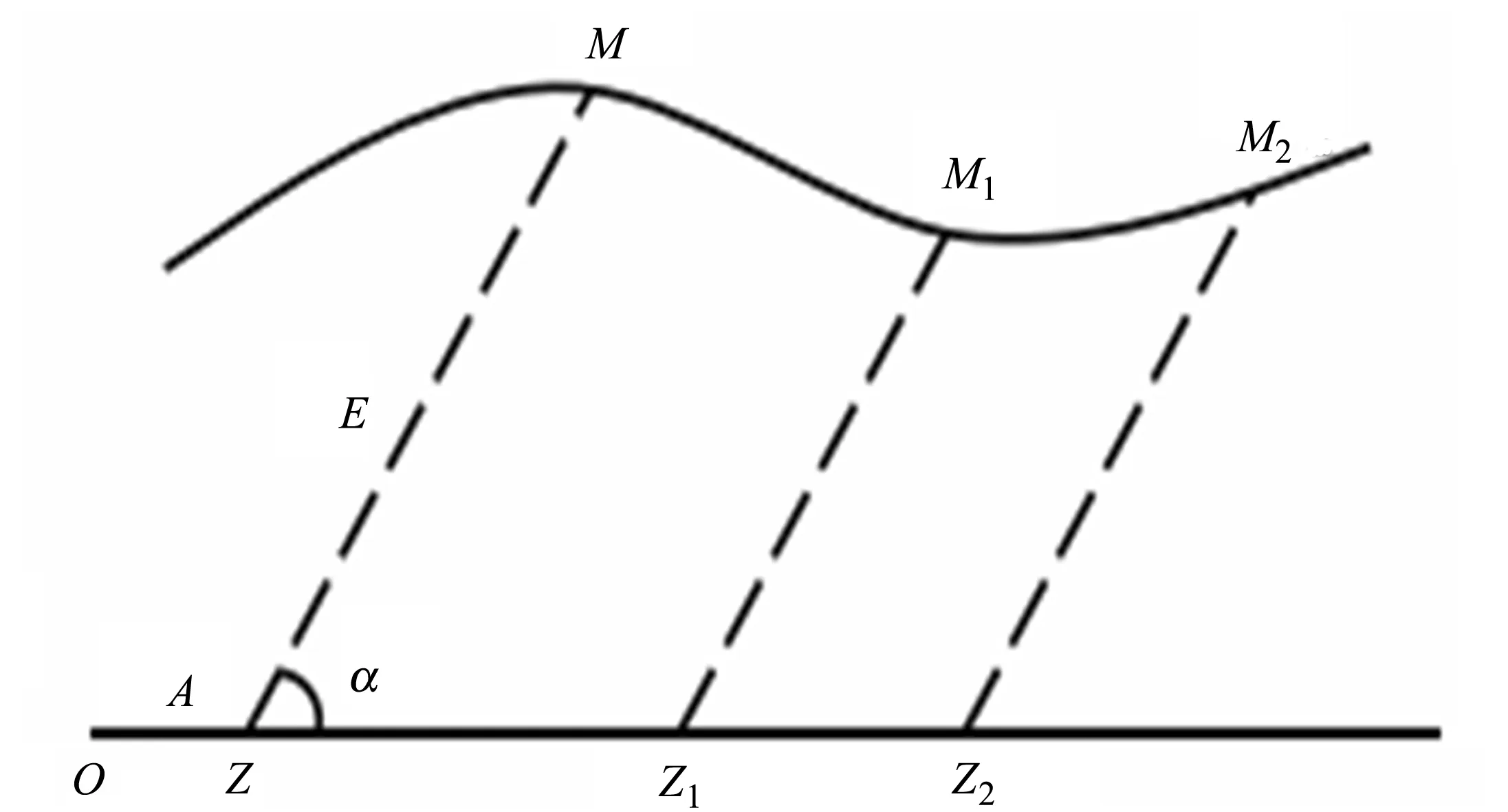
图2 费马的解析几何思想Fig.2 Analytic geometry of Fermat

为了有助于建立起方程的概念,费马引入一条水平直线OZ并确定直线上一固定点O,即将直线OZ看成x轴,固定点O为坐标原点,那么点M的位置可以由大写字母A和E来确定,其中A表示从原点O沿轴线到点Z的距离,E表示从点Z到点M的距离,其中线段ZM与轴线成固定角α。

随着A和E的不断变化,其末端M,M1,M2,…绘制出一条直线或曲线(图2)。根据这个方法,联系未知量A和E的各种方程都可以构造出相应的轨迹。

随后,费马从给定方程出发,分别研究了圆、椭圆、双曲线、抛物线等一系列曲线,例如xy=k2是一条双曲线,而形如xy+a2=bx+cy的方程通过坐标轴变换可以简化为xy=k2的形式; 证明了a2±x2=by是一条抛物线;x2+y2+2ax+2by=c2是一个圆;a2-x2=ky2是一个椭圆; 等等[6]。另外,费马还推广了阿基米德螺线r=aθ,并以代数方程定义了许多新曲线,例如被称为费马双曲线的xmym=a、费马抛物线yn=axm和费马螺线rn=aθ。

为了给出处理各种几何问题的一般方法,费马遵循前人用代数方法研究几何的思路,开创性地引进坐标工具,把曲线看成是点的运动轨迹,具有依赖关系的变量构成的方程得以被曲线表示出,解析几何思想路径为:方程(引入坐标)→点(点动成线)→轨迹。

尽管费马建立的坐标系只含一条坐标轴,但他遵循自己的思想路径揭示了解析几何的本质,即用代数方程来表示并研究曲线,其思想与现代解析几何是一致的。

对历史上积累起来的前人创造的有关科学成果的继承是科学发现的前提,没有继承就没有突破[7]。费马深深理解这一点,于是以前人的成果为出发点进行更深的数学探索,加之对问题发现的敏锐,成为解析几何的创立者之一。

3 笛卡尔与费马思想路径比较

3.1 研究目标

出于“通用数学”思想的指引,笛卡尔从帕普斯三线与四线问题出发,试图通过将几何问题转化为代数方程求解,总结出一种一般化、程序化的方法解决所有的几何问题。

费马为了修复阿波罗尼奥斯关于轨迹的一些失传的证明,继承了希腊人的思想,遵循前人用代数方法研究几何的思路,重点在于不定方程解法的图示。

3.2 研究方法

笛卡尔在处理几何问题时,首先假设解已找到,并根据已知量与未知量之间的关系构建方程,最后通过方程的求解达到解决作图问题的目的,这种从轨迹到方程的方法,正是从几何到代数的研究方向。

费马主要是完善了阿波罗尼奥斯的工作,并且沿用了韦达用字母表示数类的思想,为了寻找不定方程解法的图示,从方程出发引进坐标工具,把曲线看成是点的运动轨迹,正确叙述了解析几何的基本原理,其研究内容比较全面系统,更符合现代解析几何从代数到几何的方法[8]。

3.3 思想特点

出于其方法论原则,笛卡尔主张理性主义的直观和演绎推理,因此对传统欧氏几何方法采取摒弃态度,在解决几何作图问题过程中,巧妙地引入了变量思想和坐标观念,他的方法更具一般性,也适用于更广泛的超越曲线,从历史发展的角度看,更具有突破性[4]。

虽然费马沿袭希腊人思想的方法更为传统,但在他的工作中,用方程表示曲线的思想表现得更为明显,他对解析几何思想的阐述也比笛卡尔更系统全面,更具有启发性。

3.4 局限性

“一切问题都可归结为数学问题,一切数学问题都可归结为代数问题,一切代数问题都可归结为解方程问题。”这是笛卡尔创立解析几何思想的行动指南。由此,笛卡尔为建立普遍的、统一的“通用数学”引进了变量,并在他的《几何学》中解决了许多当时非常引人注目的几何与代数难题,为变量方法在数学中的应用开辟了一条崭新的道路,这是一项开创性的工作。法国数学家雅克·阿达玛评价道:“笛卡尔并不是修正几何,他创造了几何。”

但在另一方面,笛卡尔过于强调几何与代数的结合,对解析几何思想和方法的表述不及费马。同时,笛卡尔的数学观也造成了他在具体研究中消极的一面,他坚持亚里士多德关于“直”与“曲”有本质区别的观念,因而拒绝任何求曲线长度的探索,认为费马求极大极小值的方法和切线法则违反了严格的演绎推理的要求[9]。

与笛卡尔一样,费马建立的坐标系只含一条坐标轴,对纵坐标和如何依赖于横坐标的重视不够,因此他们所刻画的几何曲线都只是其中一部分; 同时,二人虽然都认识到了二维以上的解析几何,却没有进一步研究,三维几何直到18世纪才得到了有效的发展。

3.5 影响

解析几何把数学造成一个双面的工具,几何概念可用代数表示,几何的目标可通过代数达到; 反过来,给代数以几何的解释,可以直观地掌握那些语言的意义,又可以得到启发去提出新的结论。

17世纪中叶,笛卡尔的解析几何得到了范舒滕、沃利斯和牛顿等人的发展和传播,用代数方法研究几何问题的思想深入人心,为微积分的诞生奠定了几何学基础,扩大了数学研究的领域,从而改变了数学的面貌。

费马成功地发明了求切线、极值和面积的方法; 又用求极值的方法去求重心,将与切线有关的曲线求长问题化为一个求面积的问题; 在极其广泛的研究中应用无穷小量等,为揭示微分和积分的关系建立了良好的认识基础。牛顿在一封信中清楚地说,他从费马画切线的方法中得到了微分法的启示。费马的工作为后来欧拉、拉格朗日把几何学从现实空间图形拓展到抽象空间图形奠定了基础。后来的泛函分析、抽象代数、线性代数等的产生和发展,都由此受益[7]。正如贝尔的评价:“费马是一个第一流的数学家,一个无可指摘的诚实的人,一个历史上无与伦比的算术学家。”[10]

4 对解析几何教学的启示——数学史的教育意义

解析几何在整个中学数学中占据至关重要的地位,其思想和方法在培养学生的数学核心素养方面具有独特的意义和作用。解析几何是连接“形”与“数”两个自然界中具有普遍意义的对象的一门科学,解析几何的教学在培养学生“洞察”与“严格”的数学思维品质方面具有独特的意义和教育价值。遵循莱布尼茨的教导——“通过一些光辉的范例可以促进发现的艺术,揭示发现的方法”,通过对笛卡尔与费马创立解析几何思想路径的分析与比较,对于解析几何的数学,我们至少可以得到如下的启示与借鉴[11]。

4.1 遵循“从形到数和从数到形”的双向思维,注重几何本质

平面解析几何的基本思想有两个要点:第一,在平面上建立坐标系,平面上的点与一组有序的实数对相对应; 第二,在平面上建立了坐标系后,平面上的一条曲线就可由带两个变数(即坐标变量)的一个代数方程来表示。因此,解析几何的教学必须体现这一核心思想和方法,也就是必须遵循“从形到数和从数到形”这种双向思维的模式。这种思维模式在数学史上具有重要意义,如希尔伯特公理化体系相容性问题证明的基本思想,就遵循了这种“从形到数和从数到形”的双向思维模式,而使得非欧几何的相容性问题转化为实数算术公理的相容性问题。

基于上面的分析,解析几何有两大研究主题: (1) 如何求曲线的方程(几何问题代数化,由形到数); (2) 通过研究方程的性质(解的性质)来得到几何问题的性质(由数到形)。

4.2 突出“曲线与方程”的思想

由于解析几何的核心思想,本质而言是“曲线与方程”的思想,因而在解析几何教学中还应特别注重方程的理论及其方法的运用。在教学实践中,关于解析几何的基本思想,值得认真研究与思考的几个本质问题是: (1) 如何实现几何问题的代数化?即如何建立坐标系的问题; (2) 实现代数化的途径对其代数结论(即方程)有何影响?为什么?这就涉及坐标系之间的转化问题,即坐标变换,从而上述问题就转换为“在坐标变换下,所研究的几何问题的性质是否改变?或者说,我们所研究的问题是否是坐标变换下的不变量？”这就涉及几何学的分类问题,即F·克莱因著名的“爱尔朗根纲领”所提出的几何学分类思想。解析几何所研究的是在刚体变换群下的不变量理论,其本质仍然是属于欧氏几何的范畴,这就是为什么可以建立适当的坐标系的原因,所谓“适当”就是指不失一般性,从而不改变几何性质,将坐标系建立在最方便的位置,才有所谓的求曲线的标准方程以及将曲线的方程化为标准方程等问题。因而,所有几何性质的研究都可以在标准形式的意义下进行。上述思想在现代微分几何中得到的广泛而深入的运用,特别是在流形上的微分几何中,运用所谓的“活动标架方法”研究流形的内蕴不变量性质,可以看成是上述思想的深刻体现。

(3) 由上述方法得出的代数化的结论(方程)与几何问题(曲线)本身之间有什么样的内在关系?这就是解析几何的一个重要思想——曲线与方程的思想。研究要求这两者本质必须是一致的——即曲线是方程的曲线,而方程是曲线的方程。这就为用代数方法研究几何问题奠定了基础。