压力型锚杆灌浆体受压承载力的 计算模型与方法
2021-11-16冉孟吉涂兵雄刘超贾金青蔡燕燕张丽华
冉孟吉,涂兵雄,,刘超,贾金青,蔡燕燕,张丽华
(1.华侨大学 福建省隧道与城市地下空间工程技术研究中心,福建 厦门 361021;2.大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;3.华阳国际设计集团广州公司,广东 广州 510655;4.华侨大学 福建省智慧基础设施与监测重点实验室,福建 厦门 361021)
锚杆被广泛地应用于高边坡锚固[1-2]、深基坑支护[3-4]及抗浮结构[5-6]等工程中.根据锚杆灌浆体所受应力状态的不同,锚杆一般分为拉力型锚杆和压力型锚杆[7-8].压力型锚杆的筋体在全长范围采用套管包裹而形成全长无粘结状态,锚杆受到的荷载直接通过无粘结筋体传递至底端的承载体,承载体挤压灌浆体后,依靠灌浆体与岩土体界面的侧阻力提供承载力.因此,压力型锚杆的灌浆体处于受压状态,且承载体处的灌浆体受到的压力最大.由于压力型锚杆灌浆体处于受压状态,可采用在套管内充填油脂等防腐措施进一步提高防腐性能,故其在永久性边坡工程中得到广泛的应用[9].近年来,随着城市地下空间工程的进一步开发和利用,前期工程建设中超出建筑红线的基坑支护锚杆对地下工程建设的影响日益突出,促使压力型可回收锚杆在基坑支护等临时性工程中得到广泛的应用[10-11].压力型锚杆的破坏模式主要有筋体断裂破坏、灌浆体与岩土体界面破坏及承载体处灌浆体受压破坏[12-13].正常情况下,筋体可通过截面积设计来保证强度,极少发生断裂破坏,但灌浆体与岩土体界面破坏相对复杂,其破坏机理及界面的剪应力分布等受到学术界和工程界的较大关注,已取得较多的研究成果[14-17].在实际工程中,当压力型锚杆的锚固段较长或锚固段位于坚硬土层或风化岩层时,灌浆体因较高的抗拔承载力而难以发生灌浆体拔出破坏.此时,压力型锚杆受到的荷载可能大于钻孔中承载体处灌浆体的受压承载力,导致灌浆体发生受压破坏,继而危及工程安全[13].
压力型锚杆承载体处灌浆体的受压承载力计算是压力型锚杆承载力设计中极其重要的环节,文献[18-19]均引入有侧限锚固段灌浆体强度增大系数,以考虑承载体处灌浆体受压时,周围岩土体对灌浆体的约束效应而产生对灌浆体受压承载力提高的积极影响.然而,文献[18-19]要求该强度增大系数通过试验确定,计算取值及应用有较大困难,此外,还缺少相应的承载体处灌浆体破坏模式的分析与说明,基于围限体约束效应增强承载体处灌浆体承载力的力学机制及量化计算尚缺乏深入研究.因此,本文开展压力型锚杆灌浆体室内模型试验,分析围限体约束效应对压力型锚杆受压承载力的影响规律,并结合灌浆体受压破坏形态,探讨压力型锚杆灌浆体受压承载力的计算模型和方法.
1 试验设计
1.1 试验方案
试验方案,如表1所示.表1中:t为围限体环厚;N为试件的数量;试件组编号的G表示实心灌浆体,GH表示置孔灌浆体,数字表示试件直径(即围限体外径d1);8个试件组各包含3个试件,G50组3个试件的编号分别为G50-1~G50-3,其他类似.锚固段灌浆体采用水灰比为0.5的水泥净浆,灌浆体直径d=50 mm.灌浆体的设计有两种形式,分别为实心灌浆体(简化模型)与置孔灌浆体(实际浆体内包含有无粘结的钢绞线).实际工程中,常用的钻孔直径为130~150 mm,故配置3根直径为15.2 mm的钢绞线,按配筋率相等换算的中心置孔直径约为8.8~10.1 mm,试验取中心置孔直径为10.0 mm.围限体采用水灰比为0.4的水泥净浆进行制作,圆环状,共设计4组不同环厚的围限体(环厚分别为0,1.5d,3.0d,4.5d).试件高度参考前期研究成果的核心影响区范围,取3倍灌浆体直径,即150 mm.

表1 试验方案
试件制作方法如下.1)对于t=0的无约束围限体试件,直接在内径为50 mm的圆柱形管内灌注水泥净浆.2)对于有围限体的试件,先将外径为50 mm的聚氯乙烯(PVC)管插入底部模板的中心孔中,调整校正垂直度后,再按围限体厚度分别选用不同直径的半圆形复合模板,在两片对开半圆形复合模板外壁套设紧箍,组装成圆形模板,置于底模板,调整位置后固定;先浇筑围限体,养护28 d后拆模,缓慢旋转拔除中心的PVC管,再灌注灌浆体的水泥净浆.3)对于实心灌浆体,直接浇筑灌浆体的水泥净浆;对于置孔灌浆体,采用孔底托板固定外径为10.0 mm的PVC管后,再灌注水泥净浆.
试件的制作过程,如图1所示.

(a)制模 (b)浇筑 (c)灌浆 (d)拆模
1.2 加载方案
试验前,将灌浆体顶部加载端表面打磨至平整,然后,在围限体外壁呈180°方向对称粘贴两组应变片,每组沿试件高度按竖向间距40 mm粘贴3个应变片.加载设备采用万能试验机,加载前,在灌浆体中心安装直径为45 mm的圆柱形钢柱作为传力加载构件.对称布置两支位移计,测试加载位移,采用DH3816N型静态应变测试系统同步采集加载过程中的荷载、位移及应变数据.加载时,先以50 N·s-1的速率加载至1 kN后,卸载至0 kN,再统一以50 N·s-1的加载速率进行全程力控制加载,直至试件破坏.试件加载装置,如图2所示.

图2 试验加载装置
1.3 材料试验
制作不同规格的水泥浆试块,进行材料试验,用于测试水泥浆力学参数.材料试验,如图3所示.轴心抗压强度试验的试块尺寸为70.7 mm×70.7 mm×220.0 mm;立方体抗压强度试验的试块尺寸为70.7 mm×70.7 mm×70.7 mm;劈裂抗拉强度试验的试块尺寸为150 mm×150 mm×150 mm;三轴试验的试块直径为50 mm,高为100 mm.抗压、抗拉试验结果,如表2所示.表2中:fck,ftk,fcu,r分别为围限体的轴心抗压强度、劈裂抗拉强度和立方体抗压强度;fcu,g为灌浆体的立方体抗压强度.三轴试验共6个试块[20-23],其结果如表3所示.表3中:c为粘聚力;φ为内摩擦角.由表3可知:水灰比为0.4,0.5的试块粘聚力平均值分别为4.1,3.8 MPa;水灰比为0.4,0.5的试块内摩擦角平均值分别为42°,30°.

(a)轴心抗压强度试验 (b)立方体抗压强度试验 (c)劈裂抗拉强度试验 (d)三轴试验

表2 抗压、抗拉试验结果

表3 三轴试验结果
2 试验结果与分析
2.1 试验结果


表4 压力型锚杆灌浆体室内模型试验结果
由表4可知:除G200外,其余各组试验结果破坏荷载的相对极差最大为15.7%,最小为5.0%,整体离散性相对较小;G200-2,G200-3的灌浆体破坏荷载明显偏低,主要原因是在浇筑围限体时,因养护疏忽导致围限体开裂(图4),裂缝贯通壁环,尽管灌浆体水泥净浆渗入部分裂缝中,但该处围限体环向的抗拉承载力仍显著降低,导致围限体在内壁处为灌浆体提供的径向约束力大为减小,故试件破坏荷载明显偏低.综合对比各组数据,G200试验结果仅取G200-1为有效数据,并进行后续数据的对比与分析.
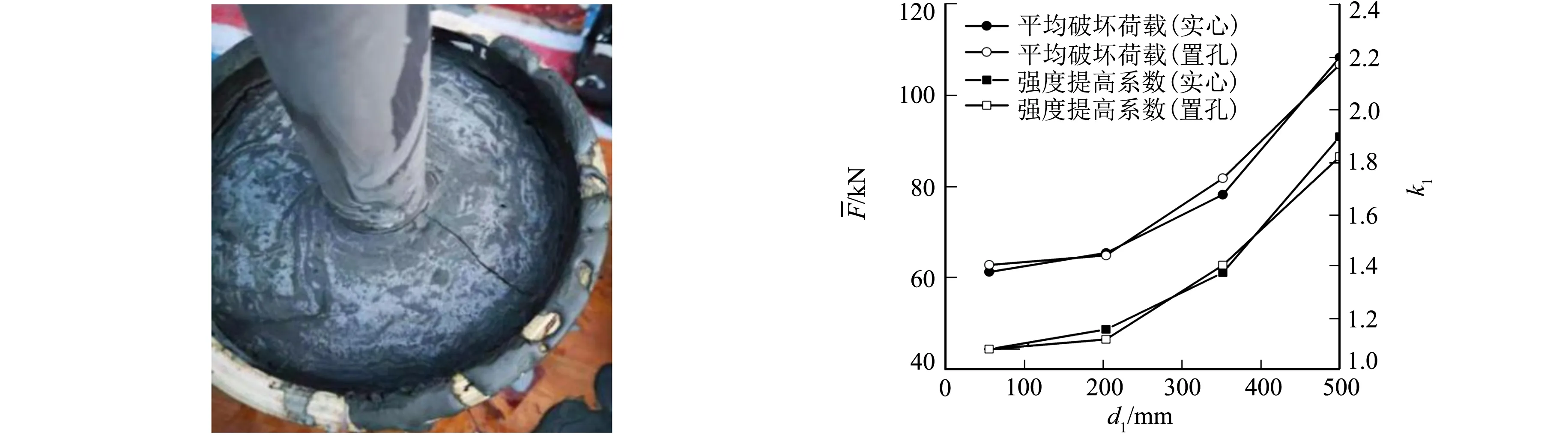
图4 围限体开裂 图5 围限体的约束效应
由表4还可知:置孔灌浆体与实心灌浆体试件的平均破坏荷载十分接近,表明灌浆体中心预留孔洞对灌浆体破坏荷载的影响几乎可以忽略;各组试件的平均破坏荷载随着围限体环厚的增加而增加.
围限体的约束效应,如图5所示.由图5可知:G200,GH200的围限体环厚仅为75 mm,尽管平均破坏荷载有所提高,但仅分别提高了8%,4%,曲线较为平缓;当围限体环厚达到150,225 mm时,实心(置孔)灌浆体试件的平均破坏荷载分别提高了31%(34%),86%(78%),围限体的约束效应导致灌浆体的受压承载力显著提高,这是因为内壁受径向应力作用的空心围限体的环厚越大,在内壁产生相同环向拉应力所需的径向应力越大,围限体内壁对灌浆体的约束作用越强,灌浆体的平均破坏荷载越大.
加载过程中,灌浆体的荷载-位移(P-s)曲线,如图6所示.
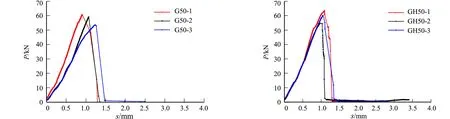
(a)G50 (b)GH50
由图6可知:对于设置围限体的灌浆体而言,荷载-位移曲线整体可分为初始弹性阶段、刚度强化阶段和破坏阶段;在初始弹性阶段,荷载随灌浆体轴向变形的增加近似呈线性增加,此阶段的灌浆体受力较小,侧向变形相对较小,围限体的约束作用尚未或较少发挥;在刚度强化阶段,荷载加载到一定程度,灌浆体侧向变形增大,围限体的约束作用得到较大发挥,灌浆体刚度有所增强,荷载-位移曲线的斜率明显增大;在破坏阶段,荷载-位移曲线迅速陡降至接近于零,表现出明显的脆性破坏特征.
2.2 破坏现象
试件的破坏过程极其短暂,破坏前,荷载-位移曲线没有明显的征兆,但部分试件的围限体出现了短暂的微小裂缝扩展过程,整体上试件的破坏具有突发性,属于脆性破坏.典型破坏现象,如图7所示.

(a)灌浆体 (b)围限体
灌浆体破坏时,圆柱形钢柱底部出现一个倒圆锥形的压密锥,压密锥的锥面有明显的破裂痕迹,小心取出灌浆体并剥离部分破碎体,在倒圆锥下方近似出现一个正圆锥,正圆锥与倒圆锥的母线近似连接成直线,且正圆锥及其底部灌浆体相对较为完好,而上部倒圆锥和下部正圆锥的锥面夹持部分沿轴向分裂成多个块体(图7(a)).由于钢柱底并不是光滑的面(实际工程中,承载体的板底也不是光滑的面),灌浆体受压后,在钢柱底部摩擦力的约束作用下,底部呈倒立的压密锥(核)形态,锥顶角为55.4°~63.8°.当荷载继续增加,随着轴向位移的增加,压密锥的锥面对四周的灌浆体产生剪切和挤压作用力,当围限体对灌浆体约束力及底部正圆锥表面的作用力无法与其平衡时,围限体开裂,灌浆体破坏.
试验过程中,荷载加载到一定值后,围限体内壁先出现数条微小裂缝,当荷载继续增大时,裂缝进一步扩展,直至出现“砰”的声响,试件迅速破坏,围限体裂缝贯穿外壁.围限体典型破坏主要表现为围限体被3条径向贯通裂缝分割为3块,相邻裂缝夹角近似呈120°(图7(b)).依据试验观测的现象,围限体破坏时并非沿环厚呈单纯的受拉破坏,而是在近内壁一定范围先出现受拉开裂,然后,在灌浆体对围限体内壁的径向压力作用下,对未开裂的围限体产生较大的劈裂作用,引发瞬间的劈裂破坏.
3 灌浆体受压承载力模型与计算
3.1 计算模型
结合试验中灌浆体的破坏现象,采用压锥模型计算压力型锚杆承载体底部灌浆体的受压承载力.当灌浆体破坏时,底部灌浆体可划分为压密锥(Ⅰ区)、破坏区(Ⅱ区)及弹性区(Ⅲ区),压锥模型图,如图8所示.图8中:σ为承载体作用在灌浆体上的压应力(即受压承载力计算值);σa为灌浆体受压后,受到围限体约束的压应力(内孔受均匀压应力);d0为为承载体直径;FG为承载体作用于灌浆体的界面;AB为灌浆体底面;AE,BD均为破裂面;点C为Ⅰ~Ⅲ区的交汇点.

图8 压锥模型图 图9 Ⅰ区受力图 图10 Ⅱ区微单元受力图
为了简化理论推导过程,对压锥模型做以下4个假定.1)Ⅰ,Ⅲ区均为刚性体,锥面上服从莫尔-库伦强度准则.2)Ⅱ区破裂前、后均为刚体,忽略破裂块体间的相互作用.3)Ⅱ区灌浆体与围限体界面间的切向应力为零,法向应力沿高度均匀分布.4)Ⅰ区压密锥的锥角为主动破裂角.
3.2 计算公式的推导
取Ⅰ区进行受力分析,其受力图如图9所示.图9中:τ1为灌浆体Ⅰ区锥面上的切向应力;α为Ⅰ区压密锥的锥角,α=45°+φg/2,φg为灌浆体的内摩擦角;σ1为灌浆体Ⅰ区锥面上的法向应力.
Ⅰ区竖向受力平衡方程为
σS1=σ1S2·cosα+τ1S2·sinα,
(1)
τ1=σ1tanφg+cg.
(2)
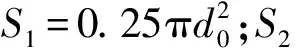
联立式(1),(2),可得
σ=cgtanα+(1+tanφgtanα)σ1.
(3)
取Ⅱ区微单元进行受力分析,受力图如图10所示.图10中:面BGG′B′为灌浆体底面微单元,过点C做面HCH′,面HCH′∥面BGG′B′;σ2为面ECE′上的法向应力;τ2为面ECE′上的切向应力;令∠HCH′=dθ.
面BCB′上法向应力σ1总合F1、切向应力τ1总合T1分别为
(4)
(5)
式(4),(5)中:r为线CH上的点到点C的距离.
面ECE′上法向应力σ2总合F2、切向应力τ2总合T2分别为
(6)
(7)
由Ⅱ区竖向受力平衡条件,可得
F1cosα+T1sinα-F2cosα-T2sinα=0.
(8)
令d0/d=m,联立式(4)~(7),并代入式(8),可得
(9)
Ⅱ区微单元面GG′E′E的法向应力产生的合力Fa为
(10)
由Ⅱ区水平向受力平衡条件,可得
T1cosα+T2cosα+Fa-F1sinα-F2sinα=0.
(11)
联立式(4)~(7)和(10),代入式(11),可得
(12)
联立式(9),(12),可得
(13)
将式(13)代入式(3),可得
(14)
3.3 围压的求解
取圆环状围限体,其内径(即灌浆体直径)为d,外径为d1,内孔受均匀压应力σa.由于假定Ⅱ区灌浆体与围限体界面间法向应力沿高度均匀分布,可简化为内孔受均匀压应力σa的圆筒.基于特定的极限状态,求得σa,将其代入式(14),即可求得灌浆体破坏时,承载体作用在灌浆体上的压应力.以下通过应变解法和应力解法对σa进行求解.
1)应变解法.对于内径为d,外径为d1,内孔受均匀压力σa的圆筒,依据弹性力学轴对称平面应力问题的极坐标解[24],有
εφ=uρ/ρ,
(15)
(16)
式(15),(16)中:εφ为环向应变;uρ为径向位移;ρ是以圆环围限体几何中心做极坐标系的极径;E,μ分别为围限体的弹性模量、泊松比.
将式(16)代入式(15),可得
(17)
当ρ=d1/2时,式(17)可变换为
(18)
将式(18)代入式(14),并令d1/d=n,可得
(19)
2)应力解法.依据弹性力学中内孔受均匀压应力σa的圆筒平面应力问题解答[24],在圆筒内壁处,环向应力与内孔压力的关系为
(20)
式(20)中:σφ为环向应力.
偏安全地,按围限体内壁环向应力达到围限体抗拉强度时,围限体破坏,同时灌浆体破坏.将式(20)代入式(14),可得
(21)
式(21)中:σt为灌浆体的抗拉强度.
3.4 对比分析
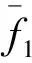

表5 受压承载力计算结果与试验结果的对比
由表5可知:G200,G350,G500应变解法计算值与试验值吻合较好;G200,G350,G500应力解法计算值中,G200的计算值偏大,G500的计算值明显偏低,G350的计算值与试验值吻合最好,表明围限体外径越大,应力解法计算值越低于试验值,理论计算结果偏于保守.应力解法与应变解法的结果存在差异的原因在于应变解法是基于实测围限体外壁环向应变进行求解,而应力解法是假定围限体内壁环向应力达到抗拉强度,对于内壁内孔受均匀压应力的空心圆柱围限体,G200,G350,G500在内壁处的内孔压力与环向应力比值分别为0.88,0.96,0.98.因此,应力解法分别求解的内孔压应力相差不大,计算的受压承载力变化不大,导致围限体直径越大,计算偏差越大.
在实际工程中,锚杆锚固段设置于地层中,灌浆体周围岩体可视为无限体,岩体不会出现试验中有限厚度围限体开裂的现象.因此,基于围限体开裂破坏的应变解法仅适用于室内模型试验,且能有效验证试验结果与应变解法结果的良好吻合性.应力解法是基于钻孔孔壁岩体的环向应力达到岩体抗拉强度(即内壁处于开裂的临界状态),所得到的灌浆体受压承载力,应力解法可同时适用于室内模型试验与工程实际情况.
受压承载力计算值与试验值,如图11所示.图11中:f为受压承载力.由图11可知:当围限体外径为350 mm时,应力解法计算值、应变解法计算值和与试验值十分吻合;当围限体外径为500 mm(围限体直径与钻孔孔径比为10)时,应力解法计算值比试验值、应变解法计算值偏低约29%,其主要原因是应力解法基于弹性理论厚壁圆筒理论,内壁环向应力随壁厚的增加存在临界现象.在实际工程中,综合考虑锚杆间距与钻孔直径的关系(锚杆间距一般约2.0 m,钻孔直径约为150~250 mm),以及岩体中包含节理和裂隙导致抗拉强度(浆液充填)一般低于相应岩石的抗拉强度,采用应力解法计算压力型锚杆灌浆体受压承载力仍是可行的.
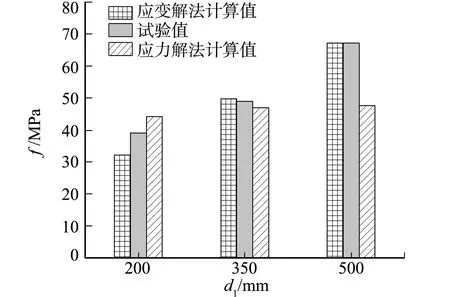
图11 受压承载力计算值与试验值
4 结论
1)压力型锚杆灌浆体的受压承载力随围限体直径的增大而明显增加,围限体对灌浆体的约束效应较为明显.灌浆体中心预留单孔洞对灌浆体的受压承载力影响很小,几乎可以忽略.
2)压力型锚杆灌浆体受压破坏时,灌浆体底部呈倒圆锥形破坏形态,围限体主要被3条径向贯通裂缝分割为3块,相邻裂缝夹角近似呈120°.
3)基于压力型锚杆灌浆体试验破坏形态,建立灌浆体受压承载力的压锥模型,应变解法的受压承载力计算值与试验值吻合较好;应力解法的受压承载力计算值随围限体直径的增大而低于试验值,但整体计算结果较为吻合,验证了压锥模型的合理性.
4)考虑锚杆实际施工工艺参数及岩体节理和裂隙的影响,基于应力解法的计算公式可用于估算实际工程中岩质地层压力型锚杆灌浆体的受压承载力.
