内齿轮刮齿刀修形设计及优化

苏进展, 王远庆, 魏刚, 杨羽, 常乐浩

(长安大学道路施工技术与装备教育部重点实验室, 710064, 西安)

采用滚、插一体的强力刮齿是一种高效、高精度的齿轮加工技术,其生产效率是插齿的4～4.2倍,加工精度可达DIN7级,特别适合于非贯通、无退刀槽的内齿轮加工[1-2]。近年来,国际上一些著名的齿轮公司都开发出先进的强力刮齿机床,例如Gleason公司的400/600PS、德国Pittler PV系列等,其配套的刮齿刀具与普通插齿刀在结构上十分相似,差别在于前刀面为空间平面且两侧刀刃不对称,以满足齿轮加工中连续滚切的工艺要求,从而形成原理性误差,增加刃磨的复杂性和制造成本。目前,国内外学者对刮齿技术的研究主要集中在刮齿原理和刮齿刀的设计上。毛世民等基于双自由度包络的理论,提出一种无误差刮齿刀切削刃的计算方法,并对刀具工作前角和后角进行了分析,引入一种改进的多边进给技术,减少刮削工具上凹边缘的磨损[3-6];李佳等根据空间交错轴啮合理论,提出了一种无理论误差刃形的直齿刮齿刀具设计与制造方法,并构造了剐齿机床的结构模型,进行了加工试验[7-8]。陈新春依据齿面形成原理,提出剐齿刀的数学模型,进行前、后刀面及前、后角设计。同时,提出剐齿刀齿廓修形及参数优化方法[9]。Shih等采用反向包络法计算无误差刀刃曲线,并用B样条拟合刀具齿面,再根据拟合曲面在多轴数控刃磨机上制造出无误差刮齿刀[10]。郭二廓等计算了车齿刀切削刃,并进行了刀具结构设计,提出一种多刃形刮齿刀,并对螺旋刮齿刀进行了改进,该结构可以避免摩擦和干扰,并使切削负荷均匀化[11-14]。尽管多刃形刀具的理论切削效率更高,但是其制造难度也十分大,很难实现量产。郭二廓等提出了一种用于加工渐开线齿形的锥齿刮齿刀刃形计算方法。之后针对强力刮齿技术中存在的单刃型刀具使用寿命短的问题,提出一种更为高效的新型锥形多刃刮齿刀具[15-17]。Tsai提出了一种基于共轭齿面重磨刮齿刀的方法[18]。Osafune等提出了一种用于内齿轮刮削的切削刃连续变化工作的评价方法[19]。Schulze等通过仿真分析刮齿运动的条件以及切屑形成机理,对工艺可靠性的影响进行了评估[20]。Klocke等研究了几何加工设置对刮齿切屑厚度及滑动速度的影响[21]。Moriwaki等对刮齿切削参数进行了详细的分析和设计[22]。Uriu等通过计算切削刀具参数对刮齿轴交角的有效性进行了研究[23]。Vargas等考虑局部前角对刮齿过程切削力进行了数值模拟[24]。Onozuka等提出了一种根据有效前角变化的影响来识别切削力系数的方法,并与实际测量力进行比较,将误差控制在15%以内[25]。

综上所述,国内外学者已掌握了刮齿原理,由于刮齿刀的几何结构和制造工艺的复杂性,使得高效率、高精度、低成本的刮齿刀设计与制造工艺逐步成为刮齿技术的关键。刮齿刀的切削刃是通过连续变位渐开线公式获得,称之为公式法,但是用该类型刀具加工的齿轮存在原理性误差。无误差刮齿刀设计方法是基于反向包络法,其基本原理为:从工件齿面出发,采用反向包络求出给定刃磨深度的刀刃曲线,再由一系列刀刃曲线拟合成刀具曲面;该方法计算过程复杂,刀具曲面拟合时会不可避免地产生误差,且刃磨工艺复杂,需要在多轴联动刃磨机上实现,因此在实际生产中应用较少。

首先,从齿条刀出发推导修形变位刮齿刀齿面,建立新型刮齿刀的实体模型,称之为修形齿条刀法;然后,比较由反向包络法、公式法和修形齿条刀法所建立的切削刃差异,通过修形优化减小由原理性误差造成的齿面偏差,为该新型刮齿刀的设计和开发奠定理论基础,同时也为基于刮齿技术的齿面修形提供新途径。所提出的新型修形刮齿刀是连续齿面,在刀具曲面的设计、制造工艺及刃磨等方面都容易实现。

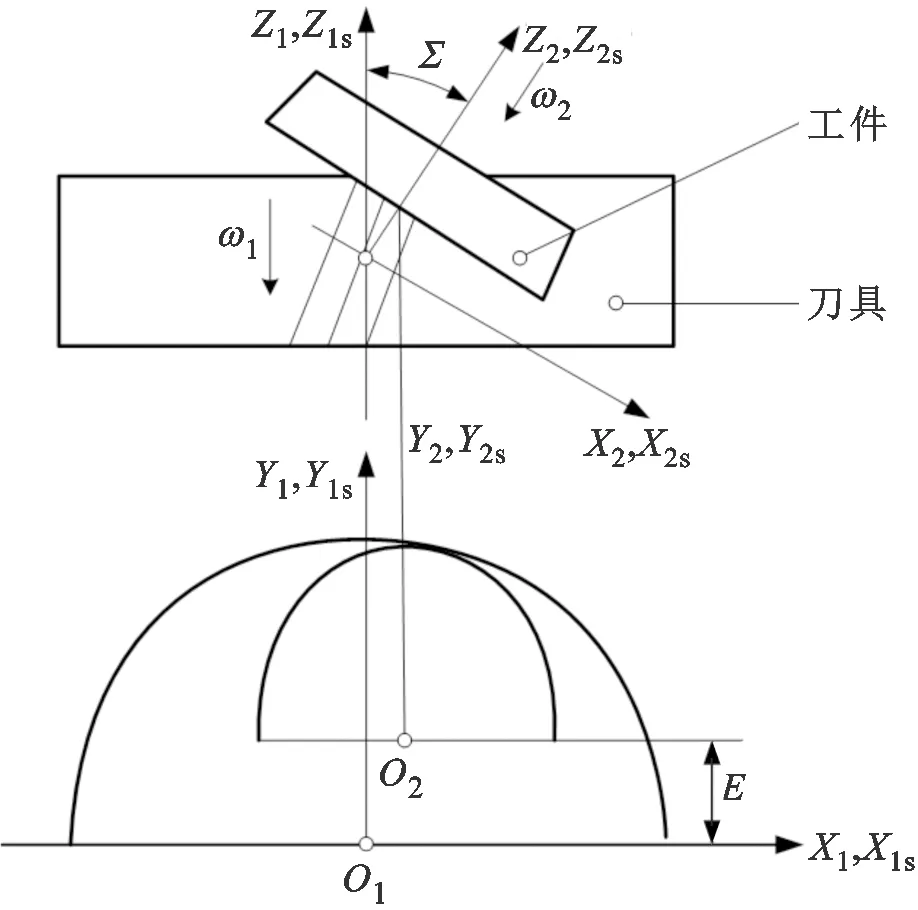
图1 刮齿原理坐标系Fig.1 Coordinate system of the gear skiving principle

1 刮齿原理

刮齿加工可视为刮齿刀与工件之间的滚插运动,即两者按照一定的滚比做滚切运动的同时,刀具沿着工件轴线做插削运动。图1为刮齿原理坐标系,表明了刀具和工件相对位置关系,S1为工件参考坐标系,S1s为工件动坐标系,S2为刀具参考坐标系,S2s为刀具动坐标系,Σ为刮齿刀和工件的轴线交角,E为中心距,ω1为工件角速度,ω2为刀具角速度,且满足

(1)

式中:z1、z2分别为工件齿数和刮齿刀齿数;vf为加工时刀具沿着工件轴向的走刀速度;p是螺旋参数。由上式可知,工件的角速度是由工件与刀具对滚的角速度和刀具轴向进给运动产生的附加转动角速度组成的。

2 刮齿刀设计

2.1 刮齿刀齿面

图2 修形齿条刀法向齿廓Fig.2 Normal tooth profile of rack-cutter with modification

将坐标St变换到Sc中得到齿条刀动坐标系的位置矢量为

rc(ut,lt)=McbMbtrt(ut,lt)

(2)

式中:Mbt为坐标系St到坐标系Sb的转换矩阵;Mcb为坐标系Sb到坐标系Sc的转换矩阵;β为齿轮螺旋角。进一步可推导出齿条刀的单位法向矢量为

(3)

图3为齿条刀加工连续变位刮齿刀的坐标系,Sa是刮齿刀的参考坐标系;Ss是刮齿刀动坐标系;齿条刀变位量xltmn中:xlt为不同齿向位置处的变位系数;变位系数xlt可由下式计算

xlt=x0cos(β)-lttan(α0cos(β))/mn

(4)

式中:x为前刀面上的最大变位系数;α为刮齿刀顶刃后角。

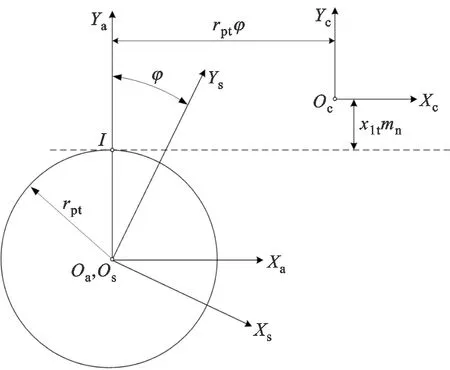
图3 齿条刀加工连续变位刮齿刀的坐标系Fig.3 Coordinate system of rack-cutter for machining skiving tool in continuous shifting

由渐开线齿轮的展成原理可知,工件转动φ,对应的齿条沿着节线移动rptφ,rpt为工件的节圆半径。由齿条刀推导刮齿刀的啮合条件为:齿条刀切削刃上的任一点与瞬心I的连线为该切削点的法向方向,即满足如下的空间直线方程

(5)

式中:xc、yc、zc为rc的坐标分量;ncx、ncy、ncz为nc的坐标分量;Xc、Yc、Zc为瞬心I在Sc中的坐标分量;Xc=-rptφ,Yc=-xltmn。可解得

φ=(xcncy-ycncx)/rptncx

(6)

通过式(6)消去工件转角φ,在Ss中刮齿刀齿面的位矢rs和法矢ns表示为

(7)

式中:Msc是Sc到Ss的转换矩阵;Lsc是矩阵Msc去掉最后一行和最后一列的矩阵。

2.2 切削刃方程

图4为刮齿刀结构示意图,与普通插齿刀的不同之处在于前刀面的定义上。刮齿刀前刀面是在前角γ的基础上,还绕着Y轴方向旋转螺旋角β,使得前刀面上的左右两侧切削刃出现不对称,切削刃在刀具端面上的投影不再是标准渐开线,从而形成了刮齿刀的原理性误差。

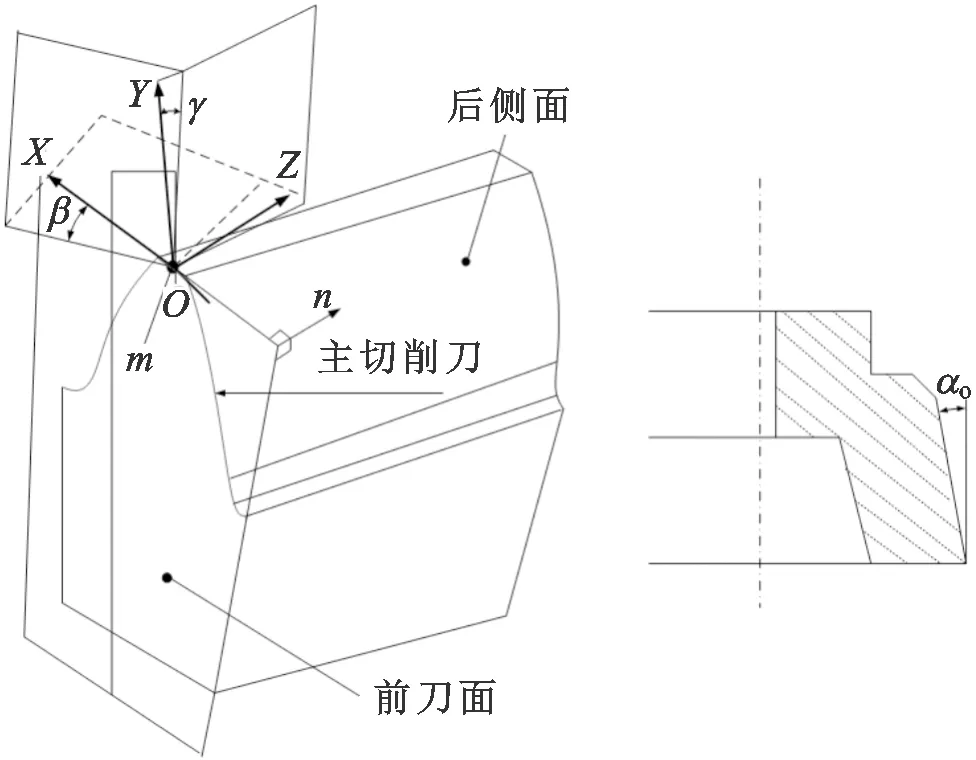
图4 刮齿刀结构Fig.4 Structure of skiving tool

取前刀面顶刃中点m为参考点,则点m的位矢rm及前刀面的法向量nm可由下式确定

(8)

其中

(9)

θ=2πh/Lt

(10)

式中:Lt为刮齿刀的螺旋导程。切削刃是前刀面和刮齿刀齿面的交线,可表示为

(11)

式中:xs、ys、zs分别为刮齿刀齿面的3个坐标分量;xm、ym、zm分别为前刀面上参考点的位矢坐标分量;r为切削刃位置参数。切削刃的切矢ts,可由刮齿刀齿面法矢ns和前面刀法矢nm得到

ts=ns(ut,lt)×nm

(12)

3 刮齿加工

图5是刮齿加工的坐标系,φ2是刮齿刀的转角;φ1是工件转角;E为中心距;v为刀具沿着工件轴向的位移;Σ为轴交角。

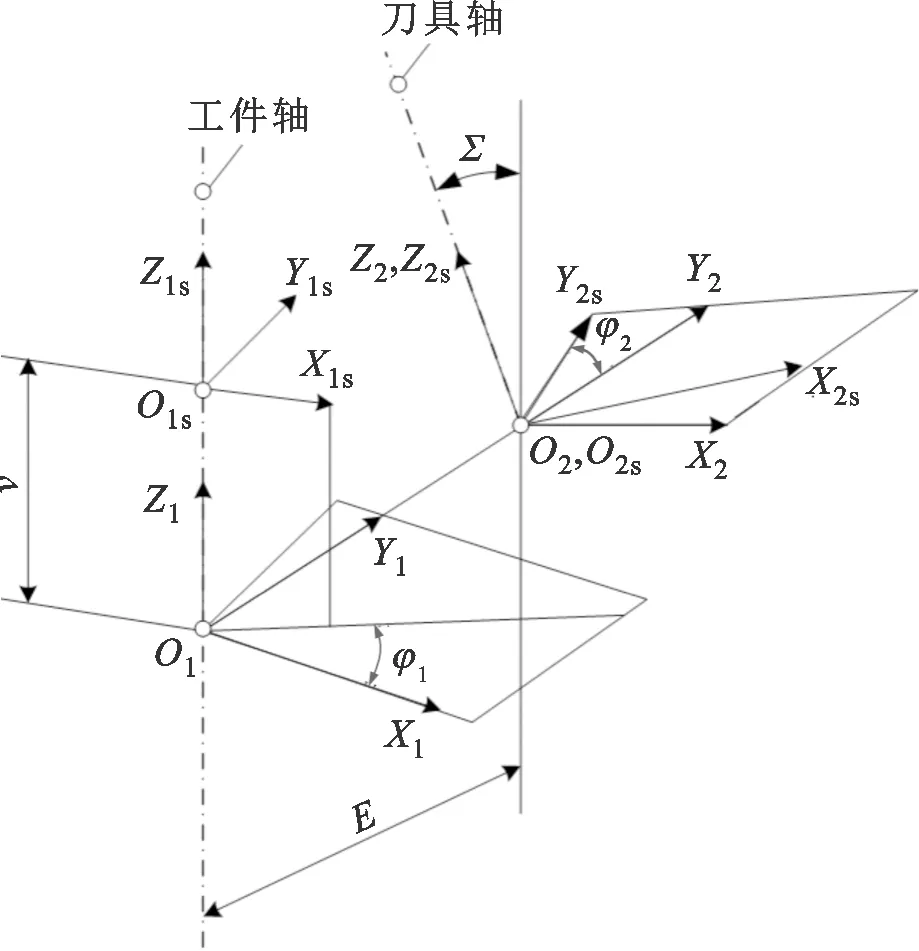
图5 刮齿加工坐标系Fig.5 Coordinate system of gear skiving

经过坐标变换,在工件动坐标系S1中,内齿轮的位矢r1和切矢t1为

(13)

式中:M2s为Ss到S2的转换矩阵;M12为S2到S1的转换矩阵;工件加工转角φ1=m21φ2+2πv/Lg;滚比m21=z1/z2;工件导程Lg=πz2mn/sinβ。根据双自由度包络原理,可得啮合方程[3]

(14)

式中:v为工件定系S1下刮齿刀与工件齿轮的相对回转运动的速度;k1为S1中z1方向的单位向量。联立式(11)(13)和(14)组成的非线性方程组,求出内齿轮的齿面方程。

4 算 例

表1为刀具和工件齿轮的基本参数,联合求解式(7)(11)得到刮齿刀齿面和切削刃上点坐标,将坐标点导入CATIA中,采用逆向建模得到刮齿刀实体模型,如图6所示。

表1 刮齿刀与内齿轮基本参数

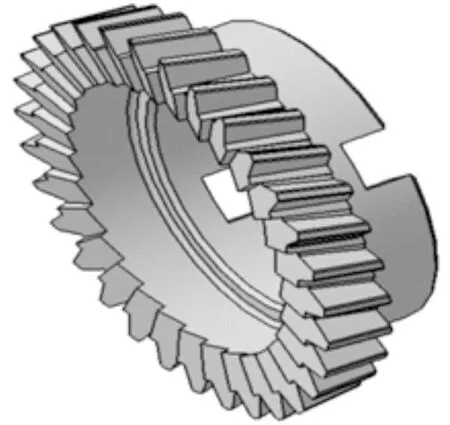
图6 刮齿刀实体模型Fig.6 Solid model of skiving tool

图7为齿条刀法、公式法和反向包络法求得的前刀面切削刃曲线。采用反向包络法可计算得到无误差刀刃曲线[8],以通过此方法求得的刀刃曲线为基准比较齿条刀法和公式法的齿面偏差。由图7切削刃曲线的局部放大图可知,齿条刀法、公式法下设计出的切削刃与无误差切削刃相比均有一定偏差,这也是导致加工时存在齿面偏差的主要原因。从图7可以看出,齿条刀法求得的刀刃曲线相比于公式法,更接近反向包络法得到的切削刃。在齿条刀法的基础上,建立以齿面偏差平方和最小为目标函数,取齿条刀的齿廓修形系数a为优化变量,采用一维黄金分割搜索法求解最佳修形系数。图7给出了修形后的刀刃曲线(a=0.001 2)与原刀刃曲线的对比,由图7的局部放大图可知,修形后的刀刃曲线更逼近反向包络法下求得的刀刃曲线。

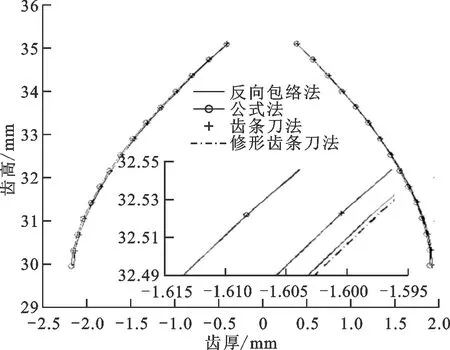
图7 切削刃曲线比较Fig.7 Comparison of cutting edge curves

以反向包络求得的工件齿面作为基准齿面,分别用公式法和齿条刀法求出内齿轮齿面,并与基准齿面比较形成齿面偏差。图8a为公式法下求得的齿面偏差图,图8b为齿条刀法下求得的内齿轮齿面偏差图,由图8可见,两侧齿面偏差均呈不对称分布,公式法的偏差最大值为24 μm,齿条刀法的偏差最大值为18 μm,采用齿条刀法获得的齿面偏差较小,这与图7中切削刃曲线接近程度相对应。图9为修形优化后的齿面偏差,显然齿面偏差最大值从原来18 μm降低到了3 μm,但仍存在两侧误差分布不均匀现象,这是由于刮齿刀的两侧切削刃不对称引起的。

(a)公式法

(b)齿条刀法图8 两种刮齿刀的齿面偏差Fig.8 Tooth surface deviations of two skiving tools

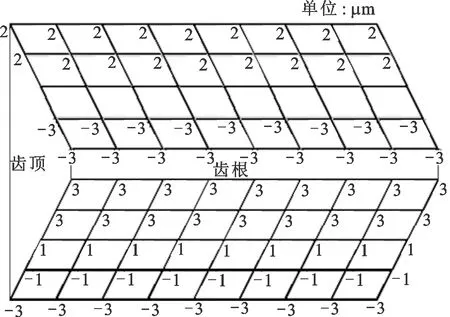
图9 修形优化后的齿面偏差Fig.9 Tooth surface deviation after modification optimization

5 结 论

以反向包络法求得的切削刃作为无误差切削刃,将其与文中采用的修形齿条刀法、齿条刀法以及公式法求得的3种切削刃进行比较分析,得到如下结论:

(1)相比公式法,齿条刀法求得的切削刃更接近反向包络法的切削刃,且获得的齿面偏差最大值较公式法降低了6 μm,这是由于两者渐开线的变位方式不同引起的。

(2)通过优化齿条刀的齿廓修形系数,使得修形齿条刀法获得的齿面偏差最大值由修形前的18 μm降低到了3 μm,修形齿条刀法能够有效地降低齿面偏差。

(3)由于刮齿刀前刀面上的左右两侧切削刃不对称,切削刃在刀具端面上的投影不再是标准渐开线。限于抛物线齿廓修形对齿面修整能力和两侧刃具有相同的抛物线系数,因此仅从齿廓修形优化很难实现将两个齿面误差同时降低到很小甚至消除。进一步,若两侧采用不同的样条曲线修形,理论上能够同时完全消除齿面偏差,其实质类似于反向包络法,但增加刮齿刀制造成本。