带参数识别的永磁同步电机多虚拟信号注入最大转矩电流比控制
2021-11-16殷凯轩高琳陈锐付文华冯智煜
殷凯轩, 高琳, 陈锐, 付文华, 冯智煜
(1.西安交通大学电气工程学院, 710049, 西安; 2.东南大学电气工程学院, 210096, 南京)
内嵌式永磁同步电机(IPMSM)体积小、结构简单,具有效率高、调速范围宽等优点[1-2],被广泛应用于电动汽车领域。如何进一步提高电动汽车的效率是目前的研究热点,最大转矩电流比(MTPA)控制充分利用磁阻转矩,可提高单位定子电流下的转矩输出能力,现有实现方法包括公式法、拟合法、信号注入法等。文献[3]给出了传统公式法的推导流程,采用拉格朗日乘子法,引入了一元四次方程的求解问题,计算复杂,不便于工程实现。文献[4]提出以去磁电流为基准将电机参数进行标幺化,通过查表得到符合MTPA控制的交、直轴电流,系统实时性得到提高,但占用了控制芯片大量的存储空间。文献[5-7]分别采用线性分段控制和拟合法对MTPA进行工程近似求解,但引入了误差项,无法实现效率最优。在实际电流中注入高频信号,对响应信号进行处理,即可得到MTPA工作点[8-9],但由于电流中含有固定频率的谐波,定子电流畸变率会显著提高,响应速度也有所降低。文献[10-11]提出了虚拟信号注入法,避免了实际信号注入带来的高频抖动等问题,但MTPA工作点跟踪精度下降。基于完整功率信息的多虚拟信号注入法(MVSI)通过数学运算求解MTPA工作点,无需带通及低通滤波器,提高了系统的响应速度[12],但多虚拟信号注入法与电机的电感、磁链参数相关,当电机参数不准确时会偏离最优工作点。因此,在多虚拟信号注入MTPA控制系统中引入适当的参数识别方法,能有效地提高控制系统的运行效率。
常见的参数在线辨识方法有最小二乘法[13-14]、扩展卡尔曼滤波法[15-16]、模型参考自适应法[17-18]等。最小二乘法计算量大,容易出现数据饱和问题。扩展卡尔曼滤波法可有效辨识电机运行状态和参数,但算法迭代需要进行大量的矩阵运算,应用领域有限。模型参考自适应参数识别(MRAS)结构简单,采用自适应律来保证各参数的收敛性,但受限于实际控制系统精度,可调模型的离散步长通常设置为10-4s,与实际电机存在精度差异,常导致辨识结果收敛至错误的值甚至发散。此外,模型欠秩问题与电感参数间的交叉耦合都会造成辨识系统的不稳定。因此,对MRAS的研究长期停留在仿真与半实物仿真阶段,实际工程领域只能对少量参数或状态变量进行在线辨识。
本文提出一种简化的多虚拟信号注入MTPA控制策略,定义了新的虚拟电压以及不完整虚拟功率,通过计算虚拟电压进而对虚拟功率进行求解,去除了基于完整功率信息的多虚拟信号注入法中的无效计算量,将算法复杂度大幅降低,但改进的多虚拟信号注入法仍然与电机电感、磁链参数相关,考虑到电机参数测量偏差以及运行时的磁路饱和效应会使电机偏离MTPA的最优运行轨迹,因此需要引入电机参数的在线辨识。为此,进一步提出改进的MRAS多参数识别算法,将自适应律分割为不同周期的函数,在Lq辨识周期内,降低Ld、ψf的辨识次数,剩余周期内固定辨识结果以减少辨识参数数量。改进的MRAS策略在一定程度上规避了模型欠秩问题,在保证三参数识别准确的同时,提高了辨识算法的稳定性,并将算法复杂度大幅降低,以适用于实际控制系统。最后,利用辨识的电机参数在线更新MTPA工作点,使电机能够始终运行在最优控制轨迹上,以达到最高运行效率。
1 IPMSM的MTPA控制原理
1.1 传统的MTPA控制方法
IPMSM在d-q坐标系下的电压方程为
(1)
电磁转矩方程为
(2)
式中:id、iq,ud、uq分别为定子d-q轴电流和电压;Ld、Lq分别为定子d-q轴电感;Rs为定子电阻;ψf为永磁体磁链;ωe为电角速度;Te为电磁转矩,np为极对数。
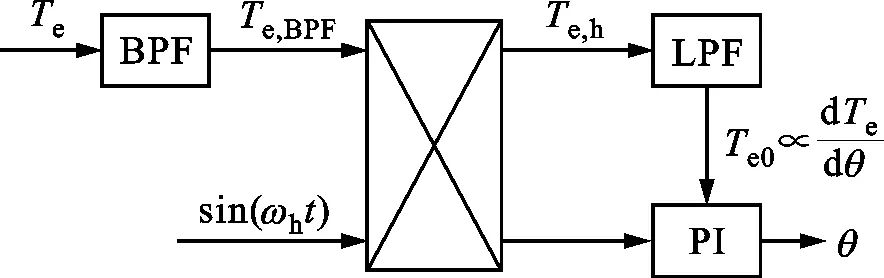
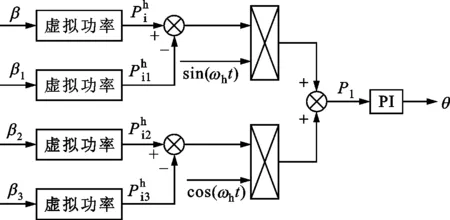
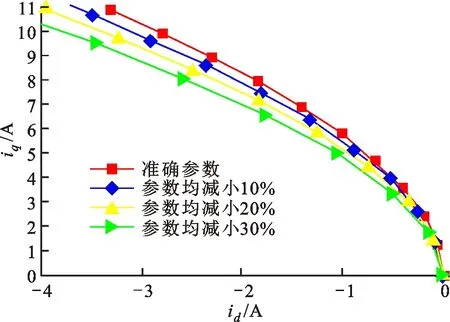
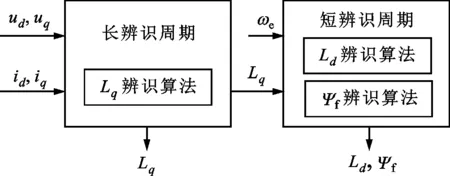
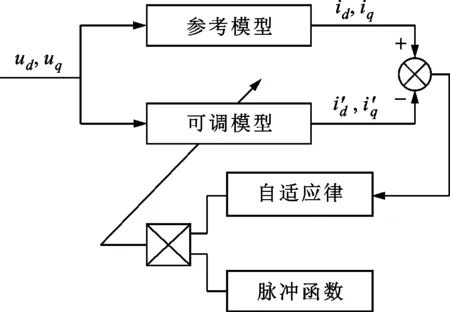
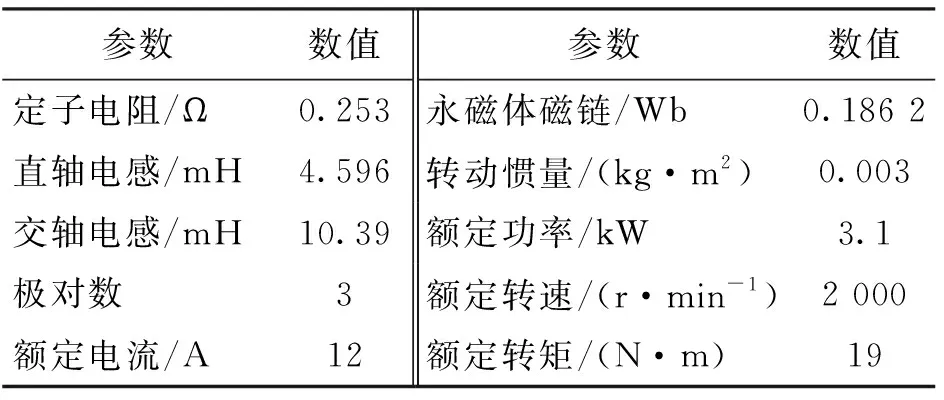
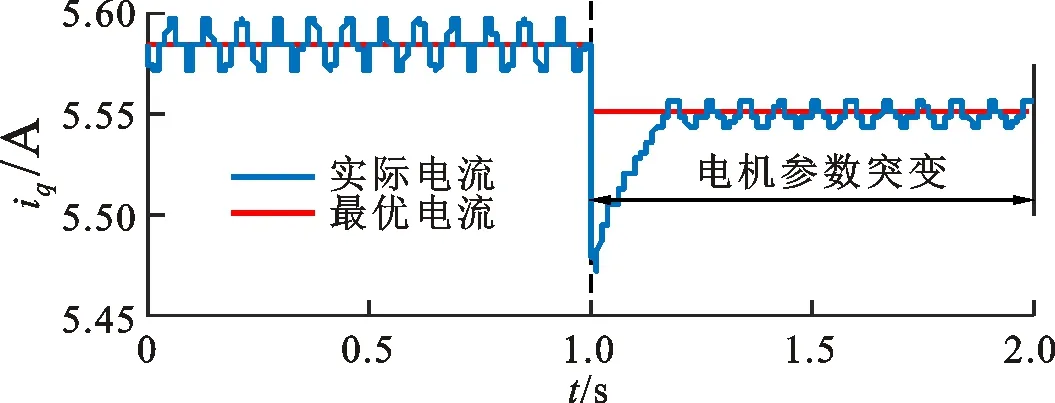
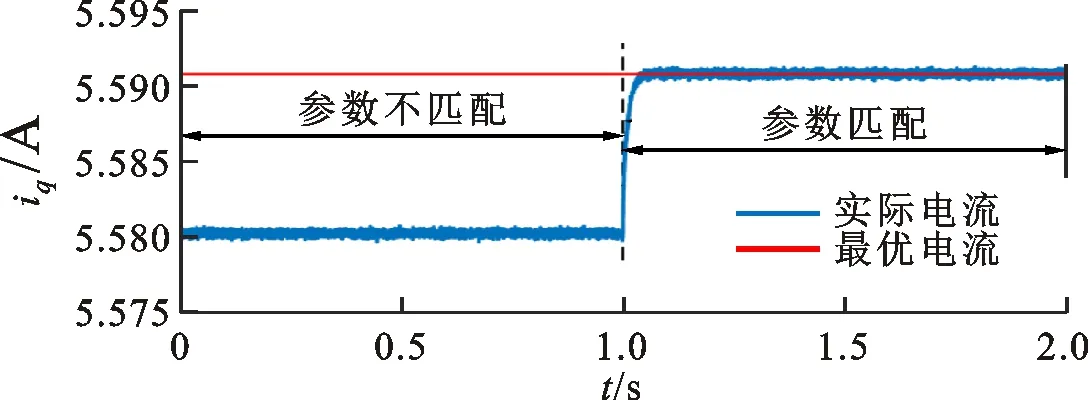
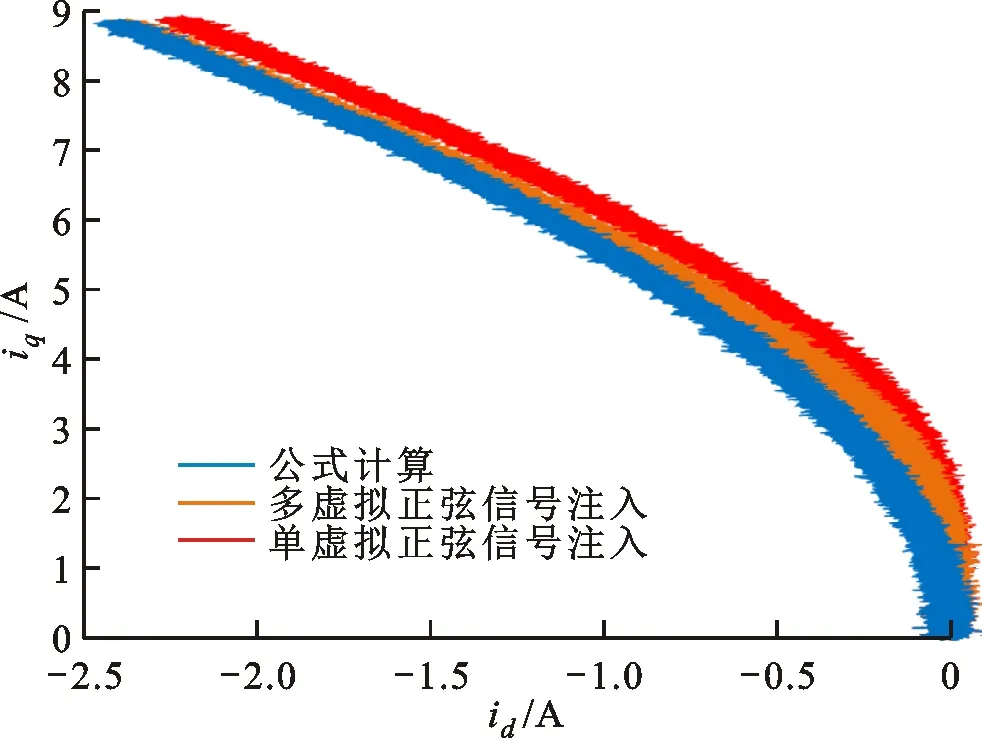
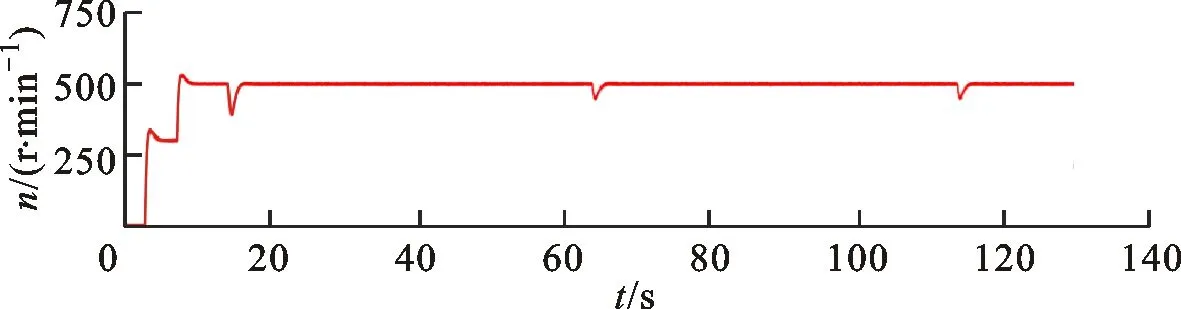
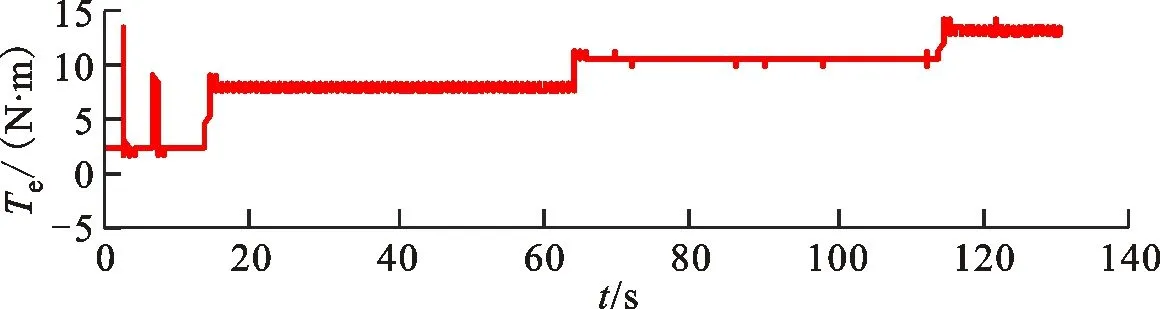
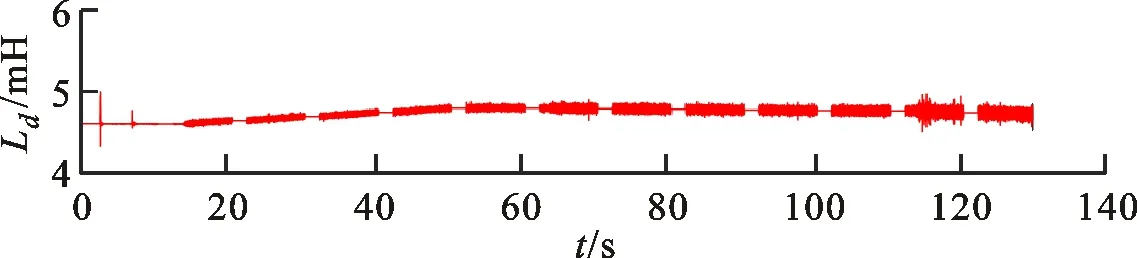
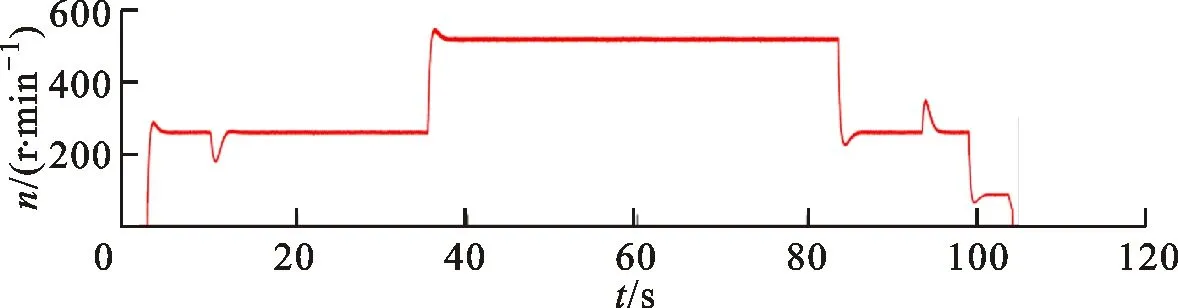
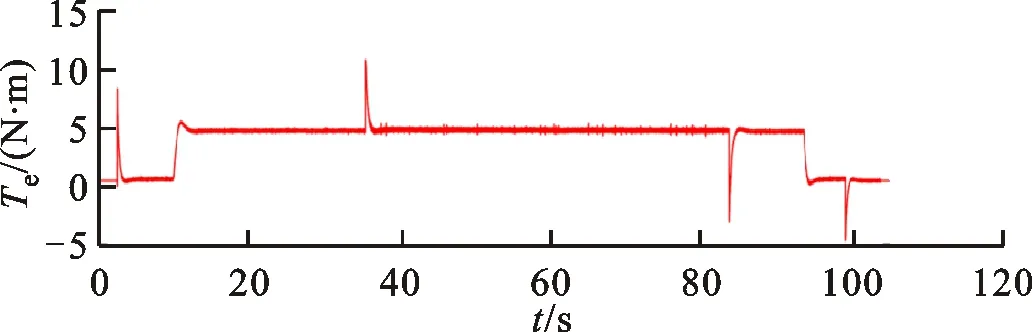
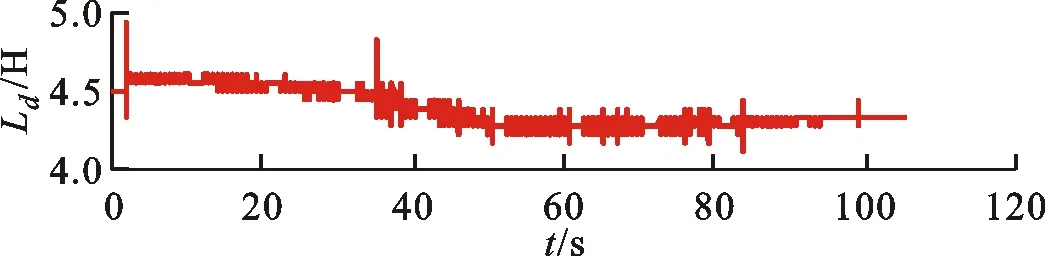
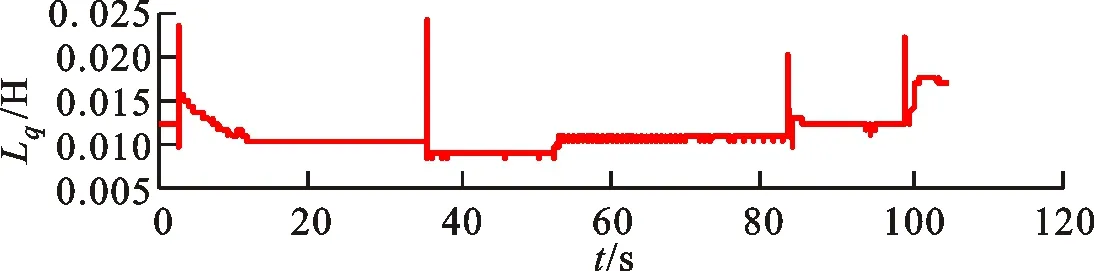
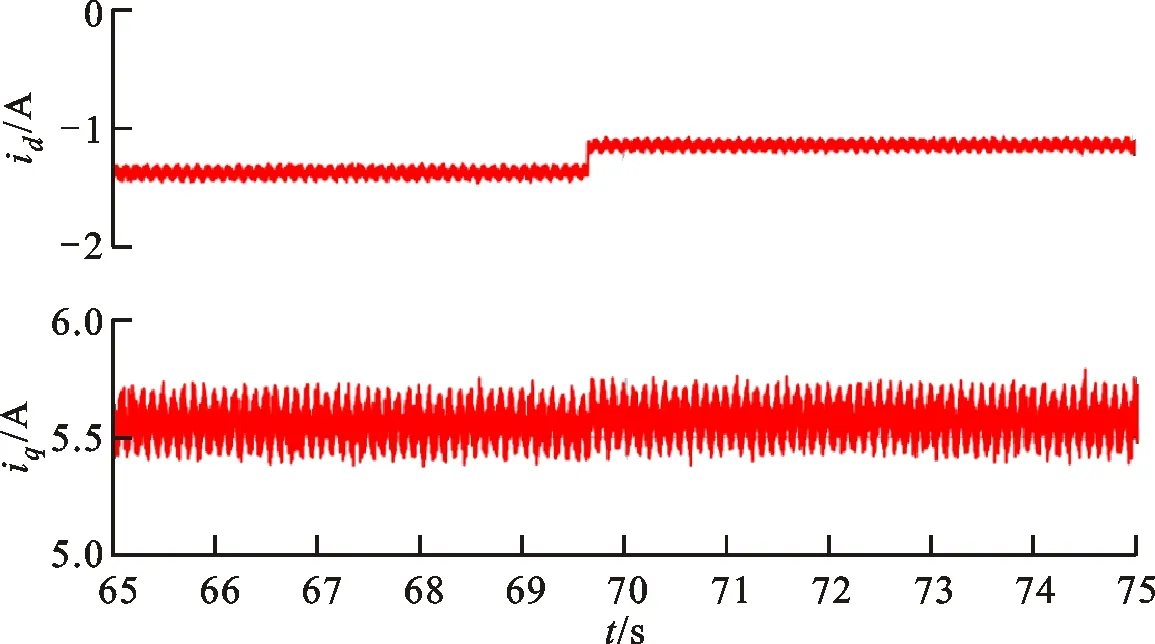
区别于表贴式永磁同步电机,IPMSM由于交直轴磁路不对称,其定子d-q轴电感不同(Ld 在输出转矩一定的条件下,通过改变d-q轴电流使得维持IPMSM正常运行所需的定子电流最小,称之为MTPA控制。此时,定子绕组铜耗最小,可以有效提高电机的运行效率。 为实现MTPA控制,传统方法是将其等效为一定输出转矩条件下求取定子电流极小值的问题,根据拉格朗日乘子法可得如下表达式 (3) 由式(3)可见,根据极值求解方法可以计算出对应MTPA状态下的d-q轴电流关系,称之为公式法。公式法求解MTPA工作点涉及一元高次方程的运算,所求d轴电流是由多参数构成的复杂、高阶函数,实用性较低,在实际工程中应用较少。 为简化MTPA工作点求解,定义转矩角θ如下 (4) 式中is为定子电流。 将式(4)代入式(2),并对θ求微分可得 (5) 结合式(2),当定子电流一定时,电磁转矩是关于转矩角的函数。以一台实际电机为例,电机参数如下:ψf=0.186 2 Wb,Ld=4.596 mH,Lq=10.39 mH。给定is=10 A,电磁转矩与转矩角的关系如图1所示,电磁转矩的最大值点即为所对应的MTPA工作点。此时,以转矩角为变量对转矩表达式进行微分运算,所求值为0(dTe/dθ=0)。 图1 电磁转矩与转矩角的关系Fig.1 Relationship between Te and θ 为避免类似于公式法的复杂计算,在实际控制系统中采用PI调节器,控制dTe/dθ为0,可以实现MTPA在线控制。采用实际信号注入法[19-20]可以获取dTe/dθ,其原理如图2所示。信号注入法(SI)通过注入高频信号并测量输出转矩,利用带通和低通滤波器提取dTe/dθ用于MTPA控制,但系统响应速度慢,对复杂工况应用效果较差。高频信号的注入导致系统中的谐波增加,电机运行时产生高频抖振。 图2 基于信号注入法的MTPA转矩角控制器Fig.2 MTPA torque angle controller based on SI 针对上述问题,多虚拟信号注入法展现出明显优势。虚拟信号对电机运行不产生任何影响,而多虚拟信号的注入使得无需采用带通和低通滤波,只需根据简单的数学运算即可获取dTe/dθ,充分利用了数字处理器运算速度快的优势,可加快系统响应速度,但该方法在计算完整虚拟功率时存在大量冗余运算,会造成运算资源的浪费。 本文提出一种基于不完整虚拟功率的MVSI方法,用于求取MTPA工作点对应的转矩角,进而实现对电机的MTPA控制。不完整虚拟功率的MVSI方法是通过定义新的虚拟电压的方式获取不完整的虚拟功率(下文简称为虚拟功率),去除基于完整功率信息的多虚拟信号注入法中的无效计算量,实现对该方法的简化。 向转矩角中注入一个幅值较小的虚拟高频信号Asin(ωht)后,对应产生的虚拟电流为 (6) 由于高频信号幅值较小,cos(Asin(ωht))≈1,sin(Asin(ωht))≈Asin(ωht)。为避免计算dTe/dθ过程中的无效计算量,定义虚拟电压为 (7) 根据输入功率表达式,推导出类似的含有高频信号的虚拟功率信息为 ωeis[ψfcosθ+(Ld-Lq)iscos2θ]Asin(ωht)+ (8) 为便于分析,可将上式写为 (9) 在同一时刻,分别注入4种不同的虚拟高频信号β=Asin(ωht)、β1=-Asin(ωht)、β2=Acos(ωht)、β3=-Acos(ωht),所得虚拟功率分别为 (10) 对所得的4个虚拟功率两两相减,可得 (11) 对得到的虚拟功率进一步处理,得 (12) 上述信号计算过程取代了传统信号处理方法中的多个滤波器滤波过程,实现原理如图3所示。 图3 多虚拟信号注入法原理Fig.3 Principle of MVSI 由式(7)~(12)可见,多虚拟信号注入法在求取MTPA工作点对应的转矩角过程中需要电机参数ψf、Ld和Lq,但是准确的电机参数通过常规的计算和实验测量往往难以获取,同时电机参数还会随运行工况实时变化。假设受温升及磁路饱和影响,电机参数ψf、Ld和Lq同时减少10%~30%,则MTPA控制轨迹也相应改变,如图4所示,不同的参数值对应于不同的MTPA控制曲线。 随着MTPA控制策略所用电机参数偏离电机实际参数越远,电机的实际运行轨迹偏离MTPA的理想运行轨迹越严重。从式(7)~(12)可以看出,改进的多虚拟信号注入MTPA控制根据不准确的电机参数求得的MTPA极值点,不再是实际电机的最优工作点,因此获取准确的电机参数在基于MVSI的MTPA控制中是非常必要的。 图4 MTPA控制轨迹随参数的变化Fig.4 MTPA control trajectory changing with parameters 考虑到MVSI对参数的依赖性,采用MRAS对IPMSM的d-q轴电感以及磁链进行辨识。MRAS系统由参考模型、可调模型和参数自适应律构成。设定实际电机为参考模型,使之与可调模型具有相同的电压输入,通过实时比较电流输出以产生误差信号e。采用合适的自适应律对可调模型的参数进行修正,当误差信号衰减为0,可调模型的参数收敛至实际值。 传统算法中,MRAS采用式(1)搭建可调模型,但受限于实验条件,可调模型的步长通常设置为10-4s,而实际电机可视为连续系统。较大的步长差异,使得相同电压输入下的两种模型存在输出误差,辨识系统本身存在的欠秩问题使得辨识结果无法收敛至准确值,因此MRAS的研究长期停滞在理论阶段,缺乏工程意义。 为了更加准确地模拟实际电机,提高可调模型的精度,离散步长带来的误差需要被进一步降低。本文提出采用四阶RungeKutta方法对IPMSM的电压方程进行离散化,原理实现如图5所示。 图5 MRAS算法原理图Fig.5 Schematic diagram of MRAS algorithm (13) 式中:id(k+1)、iq(k+1)为下一时刻可调模型的输出电流;id(k)、iq(k)为当前时刻的电流,且 由于辨识模型存在欠秩问题,可能导致辨识结果收敛错误或发散。此外,IPMSM交直轴之间存在交叉耦合,辨识结果相互干扰,使得无法对多参数同时精确辨识。为解决该问题,通常采用的方法为减少参数的辨识数量或采用复杂算法对多参数进行分步辨识。电机参数中,Lq受电机运行工况的影响最大,应在整个辨识周期内辨识,Ld受电机运行工况的影响次之,可在部分辨识周期内辨识,而ψf主要受温度影响,变化速率远低于电感,可进一步降低辨识次数。本文提出一种改进的MRAS算法,采用更连贯的方法,将自适应律分割为不同周期的函数,算法辨识流程如图6所示。 图6 所提算法的辨识流程图Fig.6 Identification flow chart of proposed algorithm 设电感的辨识周期为T,在整个周期内q轴电感以10 kHz频率进行高频次辨识。在相同的辨识频率下,d轴电感的辨识时间设定为0.8T,剩余的0.2T周期内,其辨识结果被固定以减少总的辨识参数。磁链的辨识周期设为5T,其只在0.8T周期内参与辨识,在剩余的4.2T周期内,固定其辨识结果以增加系统的稳定性。改进的MRAS策略在保证三参数识别准确的同时,提高了辨识算法的稳定性,并将算法复杂度有效降低,以适用于实际控制系统。 在参数自适应律中引入脉冲函数,利用积分的叠加性质,通过设置脉冲周期、导通时间及延迟信号,实现3个参数在不同设定周期下的辨识。改进后的MRAS算法原理如图7所示。 图7 改进的MRAS算法原理图Fig.7 Schematic diagram of improved MRAS algorithm 根据式(1),参考模型可以被简化为 (14) (15) 式(14)减去式(15),可以得到误差信号的状态方程 (16) 式(16)可以被视为标准的负反馈系统,其正向通道线性定常,反馈通道存在非线性环节。为保证系统的全局稳定,采用Popov超稳定性理论对参数自适应律进行设计,则传递函数矩阵H(s)=(sI-A)-1必须严格正定,并有以下不等式 (17) 式中r0为有限正实数。 以Lq的辨识为例,将W与e分别代入式(17),展开并分解得到 (18) 采用PI形式设计自适应律,求解式(18)可得 (19) 同理,可得 (20) 仿真与实验采用的IPMSM参数如表1所示。 实际的高频信号注入法在控制过程中无需电磁参数,因此对参数变化不敏感,仿真结果如图8和图9所示。仿真中,0~1 s内电机参数不变,第1 s时电机参数突变(变化幅度为30%)。由图可以发现,电机参数变化前后的实际d-q轴电流均围绕最优值波动,电机运行效率较高,但由于电流中含有固定频率的谐波,因此定子电流畸变率升高,并且电机运行也会出现振荡现象,因此影响了电机的控制精度。 表1 电机主要参数 图8 信号注入法d轴电流波形Fig.8 d-axis current waveform of signal injection method 图9 信号注入法q轴电流波形Fig.9 q-axis current waveform of signal injection method 图10 改进多虚拟信号注入法d轴电流波形Fig.10 d-axis current waveform of improved MVSI 多虚拟信号注入法在计算过程中需要采用IPMSM的电磁参数,若所采用的参数与实际参数不同,则最终MTPA控制结果与最优解之间也会存在偏差,如图10和图11所示。仿真中,0~1 s内模拟电机参数非线性变化的工况,将MTPA控制器中的参数改变(变化幅度为30%),在第1 s后引入参数识别结果作为控制参数。由图可以发现,0~1 s内实际d-q轴电流与最优电流存在差别,采用不准确的电机参数时定子电流约为5.75 A,引入参数识别结果后定子电流约为5.7 A,即电机参数不准确导致定子电流增加了约1%,电机运行效率降低,而通过参数识别获取准确的电机参数可解决该问题。 图11 改进多虚拟信号注入法q轴电流波形Fig.11 q-axis current waveform of improved MVSI 从仿真对比可知,实际信号注入法对电机运行影响较大,在追求高精度、高稳定性的应用领域实用价值不高。本文所提出的多虚拟信号注入法控制性能较好,但采用该方法时,电机参数的准确性决定了电机的运行效率。因此,需要采用参数识别方法实时更新多虚拟信号注入法中的定子d-q轴电感以及磁链来克服其参数依赖性。 进一步对所提出的多虚拟信号注入法的控制精度进行分析,电机参数固定为准确值,负载转矩从0斜坡上升至8 N·m。通过仿真对传统公式法、单虚拟信号注入法和所提出的多虚拟信号注入法的控制精度进行对比,分别计算3种MTPA控制策略所对应的d-q轴电流,绘制如图12所示的MTPA控制轨迹图。 图12 MTPA控制轨迹图Fig.12 Control trajectory of MTPA 当电机参数准确时,公式法对应的MTPA控制轨迹为最优轨迹。从图12可知,轻载状态下,多虚拟信号注入法的控制精度略低于公式法。随着负载增加,所提出方法的控制精度与公式法基本一致,并且全工况下的多虚拟信号注入法的控制精度均优于单虚拟信号注入法。综上,本文所提简化MTPA策略,既降低了算法复杂度又具有较高的控制精度,因此在保证控制性能的同时可以降低控制系统的硬件成本。 搭建如图13所示的基于dSPACE的永磁同步电机控制平台,对本文所提出的策略进行实验验证。转速环与电流环均采用PI控制器,电流分配策略采用所提的改进多虚拟信号注入法MTPA控制。 图13 永磁同步电机控制平台Fig.13 Control platform of PMSM 实验平台总体框架如图14所示。在MATLAB中搭建RTI模型,并导入dSPACE中,进一步通过ControlDesk软件进行调试与采样信号的调理,最终进行实验并记录实验波形。 图14 实验平台总体框架Fig.14 Overall framework of experimental platform 首先在频繁变速、变载的复杂工况下,对所提MRAS参数识别算法的稳定性及辨识效果进行探究。给定转速n=300 r/min,电机空载启动,运行稳定后再升速至500 r/min,此后一段时间内,分别施加载荷4、6及8 N·m。实验波形如图15所示,可以看到,随着载荷的增加,受磁路饱和影响,Lq和ψf均有所减小,所提MRAS参数识别算法在复杂工况下能够保持稳定,同时可以快速准确地辨识出电机参数。 (a)转速响应波形 (b)转矩响应波形 (c)Ld辨识波形 (d)Lq辨识波形 (e)ψf辨识波形图15 不同载荷工况下的实验波形 Fig.15 Experimental waveforms under different load conditions 在不同载荷工况实验中,将辨识参数与表1所示电机额定工况参数分别代入所提MTPA控制策略中,对定子电流幅值进行定量分析并用于验证MRAS参数识别算法的有效性,结果如表2所示。 表2 不同载荷下的定子电流幅值 从表2可以看到,由于不同载荷下电机参数是变化的,与采用表1参数的控制性能相比,将辨识参数代入MTPA控制策略后的定子电流均减小,说明电机的控制轨迹更接近MTPA的最优控制轨迹,本文所提MRAS参数识别算法是有效的。 下面,进一步探究引入MRAS参数识别后的多虚拟信号注入MTPA控制算法的控制性能。给定转速n=300 r/min,电机空载启动,运行稳定后突加负载转矩4 N·m,并升速至600 r/min,将控制参数增大至1.4倍,用以模拟受磁路饱和影响,电感、磁链减小30%的工况。待参数识别结果收敛后,实时更新MTPA工作点,提高IPMSM的运行效率。 图16为电机运行时的实验波形,可以看出,采用所提出的多虚拟信号注入MTPA控制策略,在控制参数与实际电机参数不匹配时,仍能保持较好的动态响应速度和较小的电流畸变率。 (a)q轴电流响应波形 (b)d轴电流响应波形 (c)转速响应波形 (d)转矩响应波形图16 电机运行时的实验波形Fig.16 Experimental waveforms of motor in operation (a)Ld辨识波形 (b)Lq辨识波形 (c)ψf辨识波形图17 改进后的MRAS实验波形Fig.17 Experimental waveforms of proposed MRAS 图17为所提出的改进后的参数识别算法的实验波形,辨识周期T设为10 s,可以看到,在参数失配、加载、变速等复杂工况下,所提出的算法虽然在辨识d轴电感时收敛较慢,但可以实现对多参数精确、稳定地辨识。 图18为基于MVSI的MTPA控制算法在引入辨识参数前后d-q轴电流输出波形。在参数失配工况下,MTPA输出的d-q轴电流分别为-1.367 9 A和5.583 6 A,总定子电流为5.748 7 A。采用MRAS参数识别,待三参数均辨识稳定后,分别代入基于MVSI的MTPA控制算法中,最终采样得到的d-q轴电流分别为-1.124 8 A和5.592 7 A,总电流为5.704 6 A。可见,参数识别算法的引入克服了多虚拟信号注入法对电机参数的依赖性,将输入电流降低0.7%,提高了IPMSM的运行效率。 图18 基于MVSI的d-q轴电流波形Fig.18 d/q axis current waveforms based on MVSI 本文针对内嵌式永磁同步电机现有MTPA控制策略所存在的问题进行了理论分析,提出了一种简化的多虚拟信号注入MTPA控制策略,去除了基于完整功率信息的MVSI中的无效计算量,在保证控制精度的基础上,将算法复杂度大幅降低。简化的多虚拟信号注入法与改进的MRAS参数识别相结合,利用辨识的参数更新MTPA工作点可以使电机始终运行在最高效率。仿真与实验结果表明,所提策略在参数摄动、负载突变以及高低速运行等复杂工况下均能保持较好的控制性能。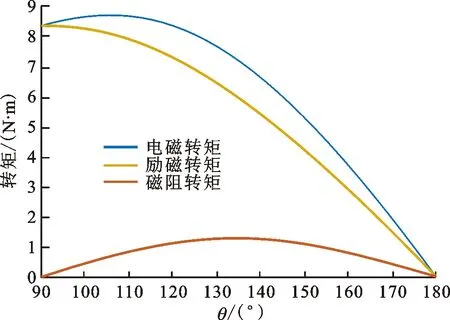
1.2 改进的虚拟多信号注入MTPA控制方法
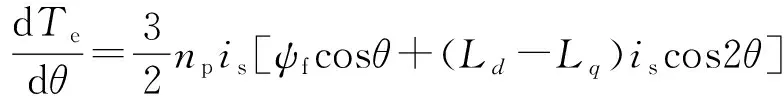
2 改进的MRAS参数识别
2.1 改进的可调模型


2.2 改进的参数识别算法
2.3 求解参数自适应律

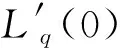
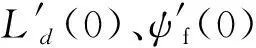
3 仿真与实验验证
3.1 仿真验证


3.2 实验验证



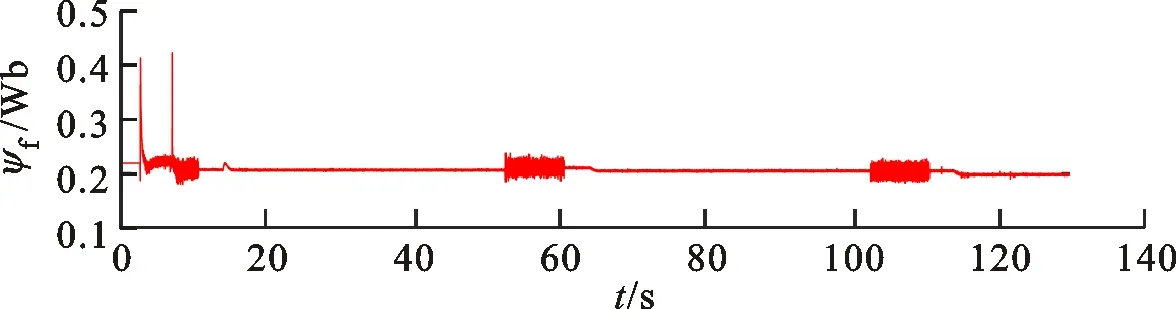
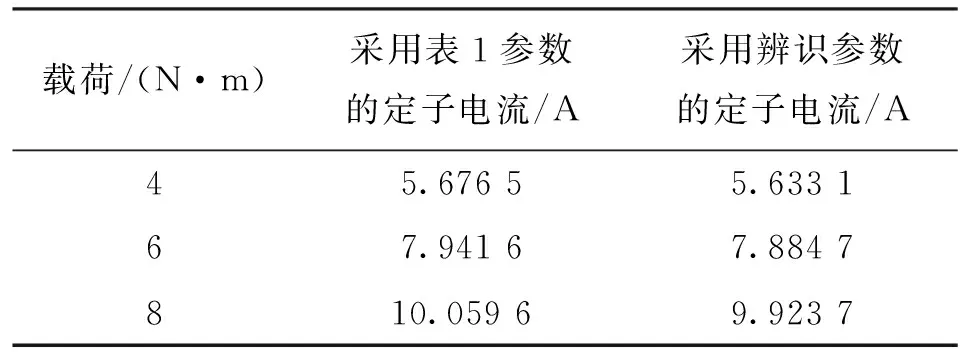
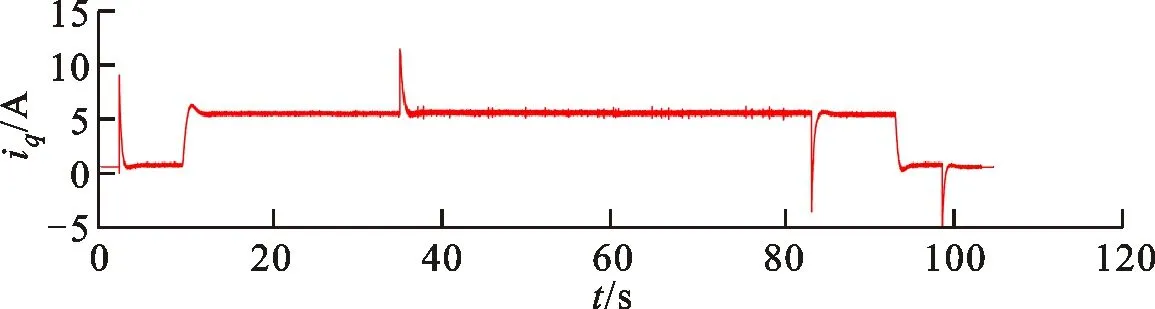
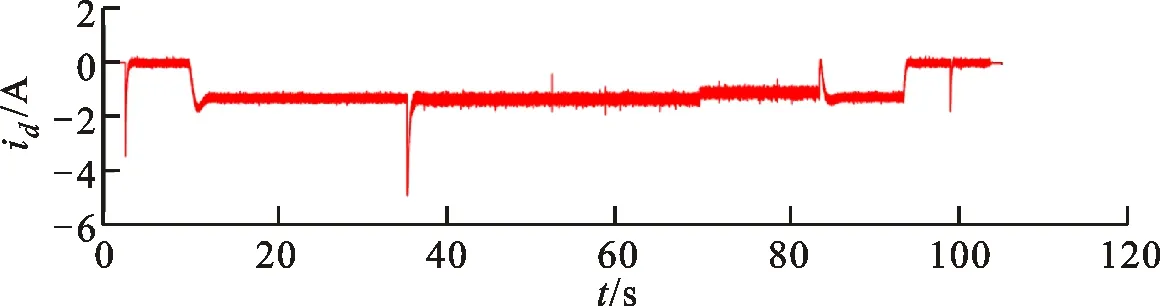

4 结 论
