基于对象和基于属性的三支概念格合并方法比较

苏 新 陈永平 杨思春

1(马鞍山职业技术学院电子信息系 安徽 马鞍山 243000) 2(安徽工业大学计算机学院 安徽 马鞍山 243000)

0 引 言

形式概念分析，又称概念格理论(一般称为经典概念格)，1982年由德国数学家Ganter等[1]提出，该理论是根据数据集中二元关系建立的一种概念层次结构，是数据分析与规则提取的一种有效工具。目前形式概念分析已在决策分析、信息检索、数据挖掘、软件工程和知识发现等领域得到了广泛的应用。

三支概念格[2]是由三支决策理论[3]与经典概念格理论相结合而产生的一种用于知识发现的理论。三支决策理论将决策问题分为三种：接收、拒绝和延迟决策；经典概念格理论只考虑某些对象共同具有内涵中的属性或者某些属性被外延中的所有对象共同拥有，而没有考虑某些对象共同不具有的属性或某些属性不被哪些对象所拥有。Qi等将这两种理论有机地结合起来，提出了负算子(共同不具有)的概念，而把经典概念格中的运算称为正算子(共同拥有)，由此可以将对象域或属性域分成三个不相交的部分，分别是正域、负域和边界域(部分拥有)。在此基础上可以得到三支概念和三支概念格，分别是由对象导出的三支概念和三支概念格、由属性导出的三支概念和三支概念格。

三支概念格提出以来，受到了学者的广泛关注，并取得了不错的研究成果。文献[4]简述了形式概念分析的优劣与三支决策理论的意义,并阐述了三支概念格产生的思想，从理论和应用两个方面梳理了三支概念格的研究成果，并对三支概念格的今后研究方向进行了展望；文献[5]给出了三支概念格的四种约简方法，并对它们之间的关系进行了讨论；文献[6]分别从元素、集合和序的角度对由对象和属性导出的三支概念格与经典概念格之间的关系进行了研究。目前对三支概念格的研究主要集中于属性约简[5,7-8]、三支概念格的构造[9]和规则的提取[10-11]等方面，而对三支概念格的合并研究较少。虽然文献[12]利用规则提取方法，通过对对象导出的三支概念格和属性导出的三支概念格的合并，给出了合并后的三支概念格的规则提取算法，但也仅仅是为了规则提取而给出一种合并方法，没有给出合并后的三支概念格的相关性质。因此，本文在文献[12]的研究基础上，提出一种基于属性为主的三支概念格的合并和基于对象为主的三支概念格的合并方法，并给出合并后三支概念格的性质，也就是对合并后的三支概念格与合并前的三支概念格和经典概念格之间的关系进行了研究。同时也对两种方法(基于属性为主的三支概念格的合并和基于对象为主的三支概念格的合并)所得到的三支概念格之间的关系进行了研究，并给出基于属性为主的三支概念格的合并和基于对象为主的三支概念格合并的算法，最后通过实例对本文提出的理论进行验证。

1 基本知识

定义1[1]设(U，M，R)为形式背景，其中U={a1，a2，…，am}，每个ai(i=1,2,…,m)称为对象,M={b1，b2，…，bn}，每个bj(j=1,2,…,n)称为属性,对于a∈U、b∈M,如果(a,b)∈R,则称对象a拥有属性b。

定义2[1]设(U，M，R)为形式背景，对于A⊆U,B⊆M，一对算子定义如下：

*:P(U)→P(M)，A*={b∈M|∀a∈U,(a,b)∈R}

(1)

*：P(M)→P(U)，B*={a∈U|∀b∈M,(a,b)∈R}

(2)

定义3[1]设(U，M，R)为形式背景，若A*=B且B*=A，则称(A，B)是一概念，A称为该概念的外延，B称为该概念的内涵。

对于任意概念(A1，B1)、(A2，B2)，定义偏序关系为(A1，B1)≤(A2，B2)⟺A1⊆A2⟺B2⊆B1，则形式背景(U，M，R)的所有概念在该偏序关系下是完备格，称为概念格，记为L(U，M，R)。

以上定义的算子是形式背景中的正算子，下面给出负算子的定义。

定义4[2]设(U，M，R)为形式背景，对于A⊆U,B⊆M，一对负算子定义如下：

(3)

(4)

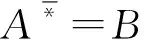
在形式背景的正算子和负算子定义的基础上，定义三支算子如下：

定义5[2]设(U，M，R)为形式背景，对于A⊆U,B⊆M，三支算子定义如下：

(5)

(6)

进一步定义该三支算子的逆算子如下：

≥：DP(M)→P(U)：(A,B)≥={a∈U|a∈A*

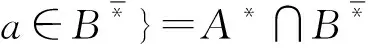
(7)

≥：DP(U)→P(M)：(X,Y)≥={b∈M|b∈X*

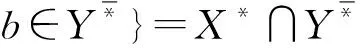
(8)

式中：DP(U)=P(U)×P(U)；DP(M)=P(M)×P(M)。

在此基础上，下面可以定义三支概念和三支概念格。

定义6[2]设(U，M，R)为形式背景，X⊆U，A,B⊆M，若X≤=(A,B)且(A,B)≥=X，则称(X，(A，B))为对象导出的三支概念，简称为OE-概念，其中X和(A，B)分别称为OE-概念(X，(A，B))外延和内涵。

若(X，(A，B))、(Y，(C，D))为形式背景(U，M，R)的OE-概念，定义偏序关系(X，(A，B))≤(Y，(C，D))⟺X⊆Y⟺(C,D)⊆(X,Y)，形式背景(U，M，R)所有OE-概念在该偏序关系下是完备格，称为对象导出的三支概念格，记为OEL(U，M，R)。

类似地，可以定义由属性导出的三支概念和三支概念格。

定义7[2]设(U，M，R)为形式背景，X,Y⊆U，A⊆M，如果(X,Y)≥=A且A≤=(X,Y)，则称((X，Y)，A)为属性导出的三支概念，简称为AE-概念，其中(X，Y)和A分别称为AE-概念((X，Y)，A)的外延和内涵。

若((X，Y)，A)、((Z，W)，B)为形式背景(U，M，R)的AE-概念，定义偏序关系((X，Y)，A)≤((Z，W)，B)⟺(X,Y)⊆(C,D)⟺B⊆A，形式背景(U，M，R)的所有AE-概念在该偏序关系下是完备格，称为由属性导出的三支概念格，记为AEL(U，M，R)。

例1在形式背景(U，M，R)中，U={1，2，3，4,5}，M={a，b，c，d},任意(u，m)∈R时，用1表示，任意(u，m)∉R时，用0表示，其对应的概念格用L(U，M，R)表示，如表1所示，其对应的概念格L(U，M，R)={(1245，a)，(123，bd)，(12，abd)，(4，ac)，(U,∅),(M,∅)}，L(U，M，R)对应的哈斯图如图1所示，而(U，M，R)的补概念格L(U，M，Rc)={(1 235，c)，(45，bd)，(5，bcd)，(3，ac)，(U,∅),(M,∅)}，其对应的哈斯图如图2所示。表1对应的AEL(U，M，R)和OEL(U，M，R)分别如图3和图4所示。

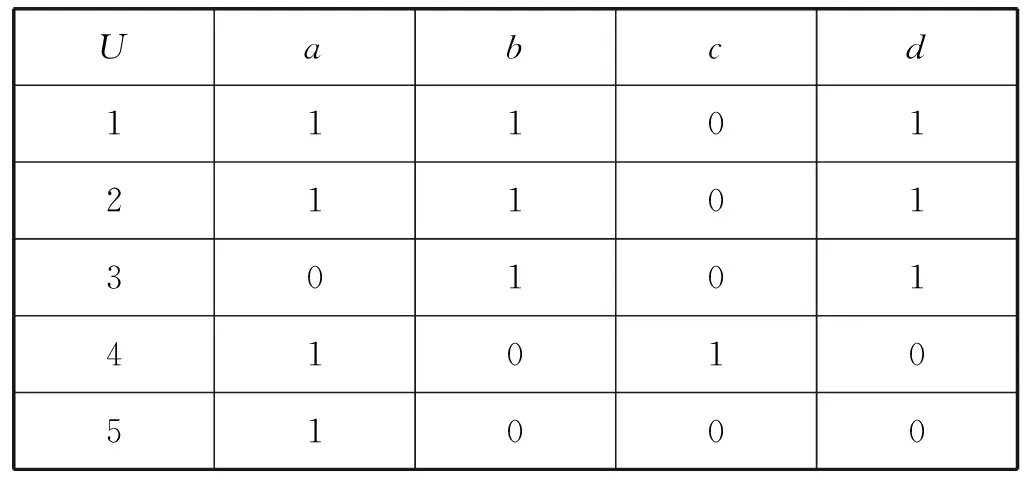
表1 形式背景(U，M，R)

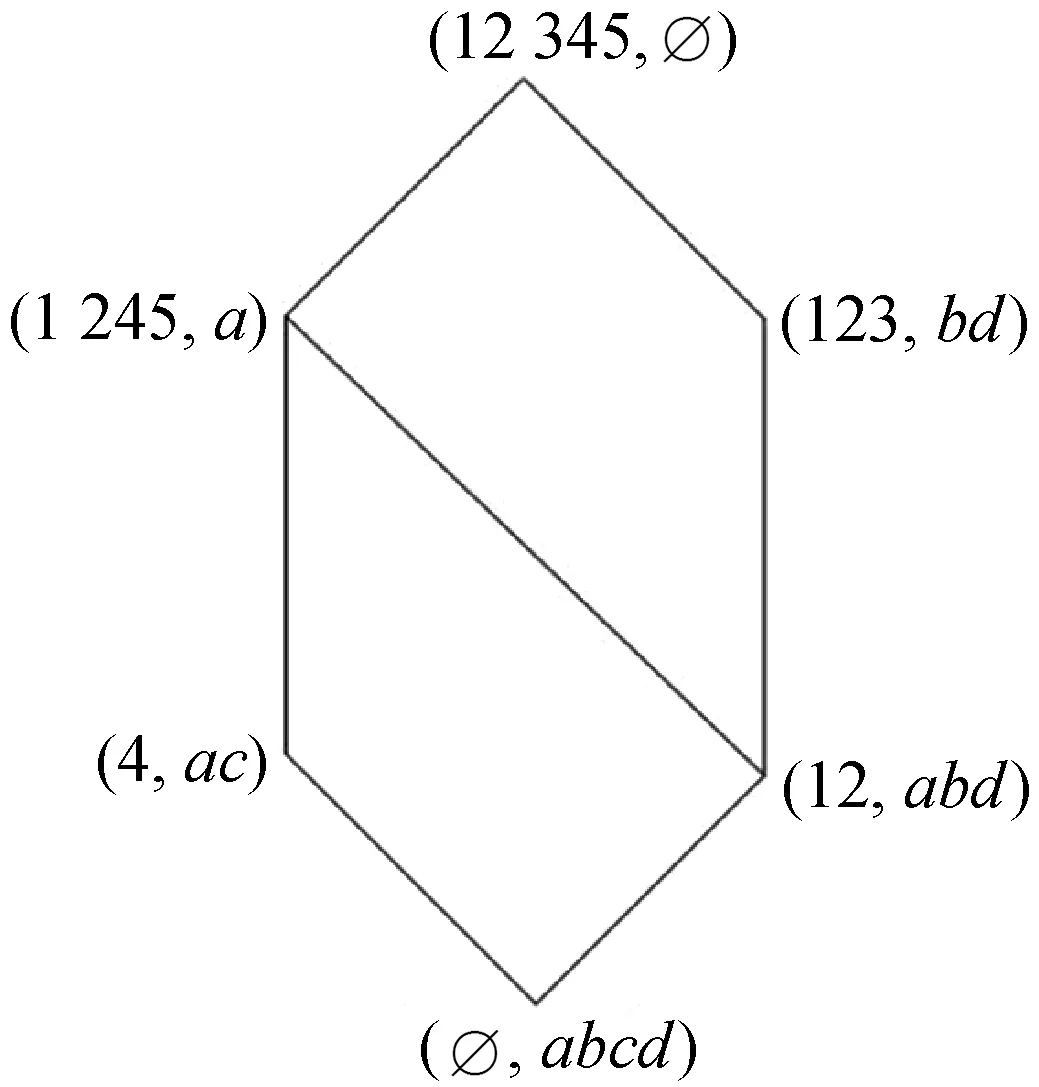
图1 L(U，M，R)

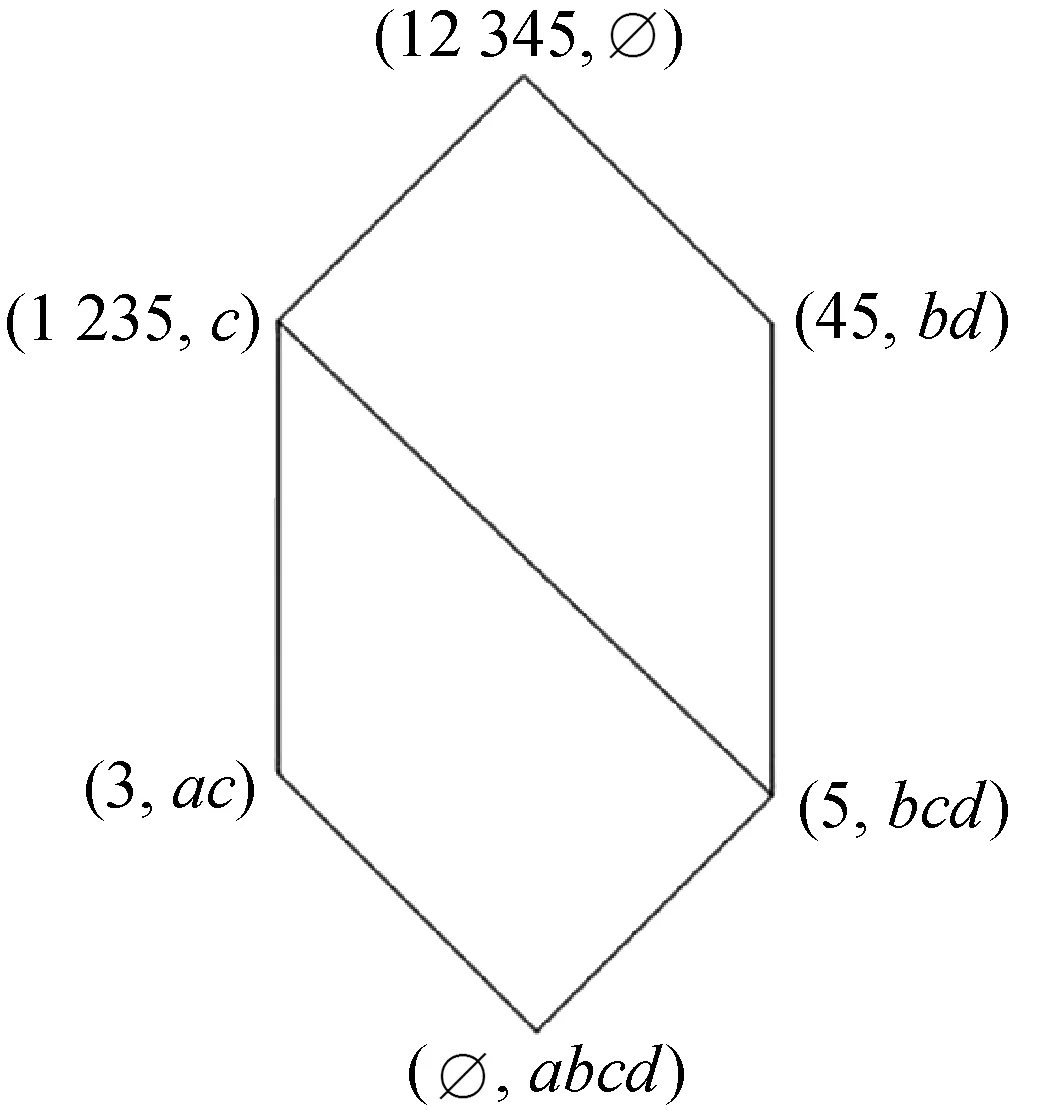
图2 L(U，M，Rc)

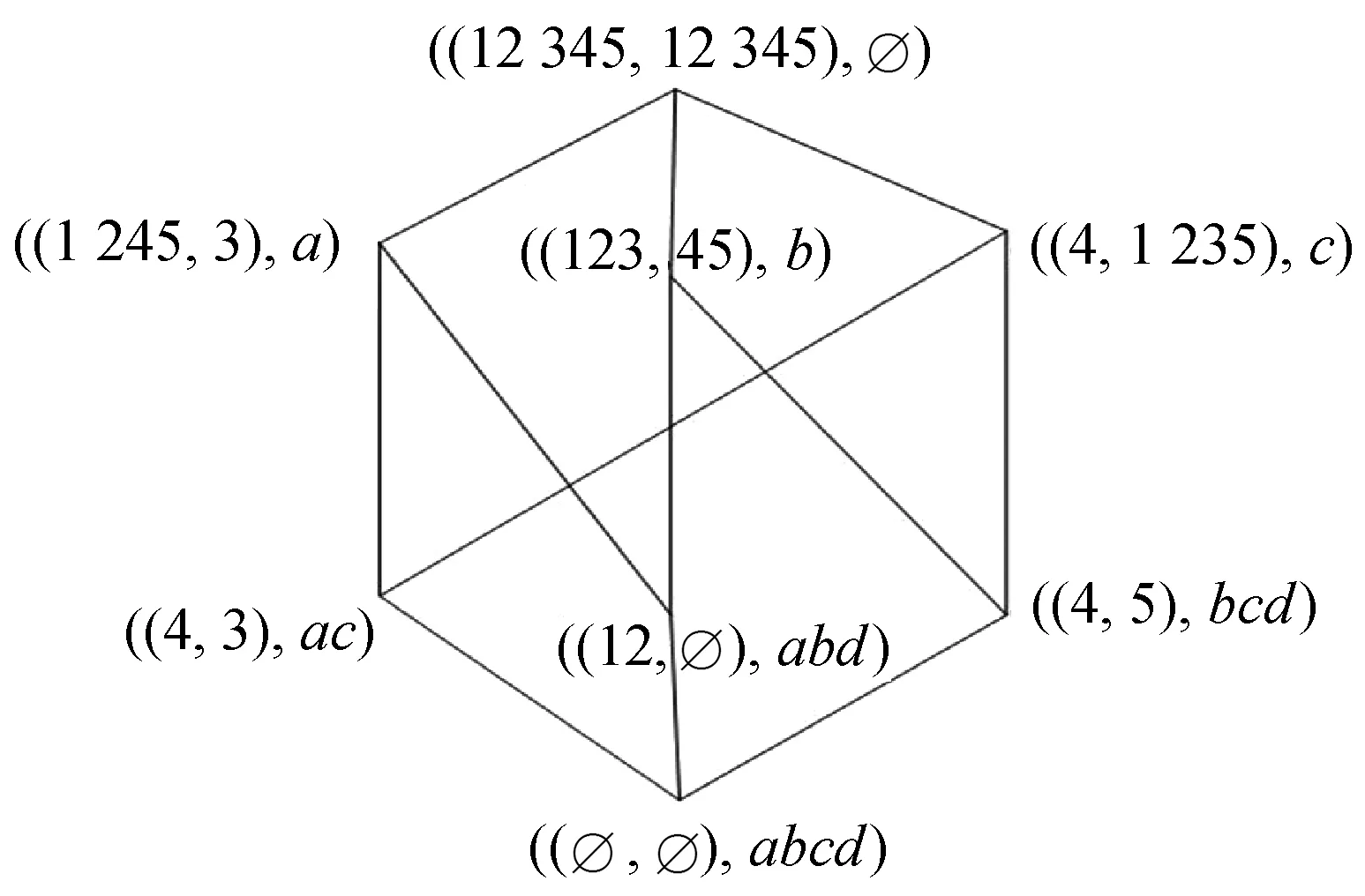
图3 AEL(U，M，R)

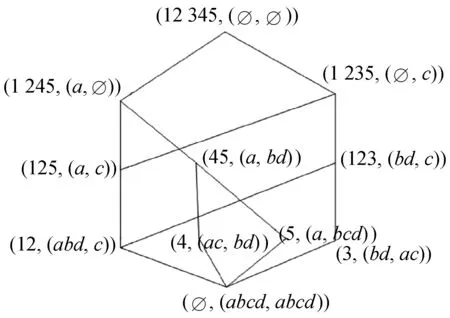
图4 OEL(U，M，R)

文献[6]给出了经典概念格与三支概念格的关系，下面给出经典概念格和由对象导出的三支概念格的关系，在此记：

定理1[6]设(U，M，R)为形式背景，(U,M,Rc)为其补背景，其中Rc=U×MR，则下列式子成立：

①LU(U,M,R)⊆OELU(U,M,R)

②LU(U,M,Rc)⊆OELU(U,M,R)

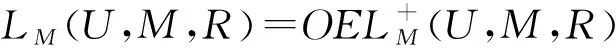
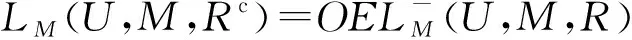
下面再给出经典概念格和由对象导出的三支概念格的关系，在此记：

定理2[6]设(U，M，R)为形式背景，(U,M,Rc)为其补背景，其中Rc=U×MR，则下列式子成立：

①LM(U,M,R)⊆AELM(U,M,R)

②LM(U,M,Rc)⊆AELM(U,M,R)

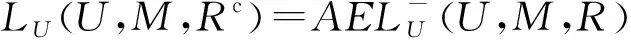
2 三支概念格的合并

2.1 基于属性为主的三支概念格合并

定义8设(U，M，R)为形式背景，若((X，Y)，A)∈AEL(U，M，R)，(X，(A，B))∈OEL(U，M，R)或(Y，(B，A))∈OEL(U，M，R)，则((X，Y)，(A，B))为基于属性为主的三支概念格合并，简称为AOE-概念。这里(X,Y)≥=A且A≤=(X,Y)，X≤=(A,B)且(A,B)≥=X，或者(X,Y)≥=A且A≤=(X,Y)，Y≤=(B,A)且(B,A)≥=Y，X⊆U,Y⊆U,A⊆M,B⊆M。(X，Y)和(A，B)分别称为AOE-概念的外延和内涵。

对于((X，Y)，(A，B))、((Z，W)，(C，D))，定义其上的偏序关系为((X,Y),(A,B))≤((Z,W),(C,D))⟺(X,Y)⊆(Z,W)⟺(C,D)⊆(A,B)，则形式背景(U，M，R)的所有AOE-概念在该定义的偏序关系下是完备格，记为AOEL(U，M，R)。

2.2 基于对象为主的三支概念格合并

定义9设(U，M，R)为形式背景，若(X，(A，B))∈OEL(U，M，R)，((X，Y)，A)∈AEL(U，M，R)，或((Y，X)，B)∈AEL(U，M，R)，则((X，Y)，(A，B))为基于对象为主的三支概念合并，简称为OAE-概念。这里X≤=(A,B)且(A,B)≥=X，(X,Y)≥=A且A≤=(X,Y)或X≤=(A,B)且(A,B)≥=X，B≤=(Y,X)且(Y,X)≥=B，X⊆U,Y⊆U,A⊆M,B⊆M。(X，Y)和(A，B)分别称为OAE-概念的外延和内涵。

对于((X，Y)，(A，B))、((Z，W)，(C，D))，定义其上的偏序关系为((X,Y),(A,B))≤((Z,W),(C,D))⟺(X,Y)⊆(Z,W)⟺(C,D)⊆(A,B)，则形式背景(U，M，R)的所有OAE-概念在该定义的偏序关系下是完备格，记为OAEL(U，M，R)。

根据定义8和定义9分别得到AOEL(U，M，R)和OAEL(U，M，R)如图5和图6所示。

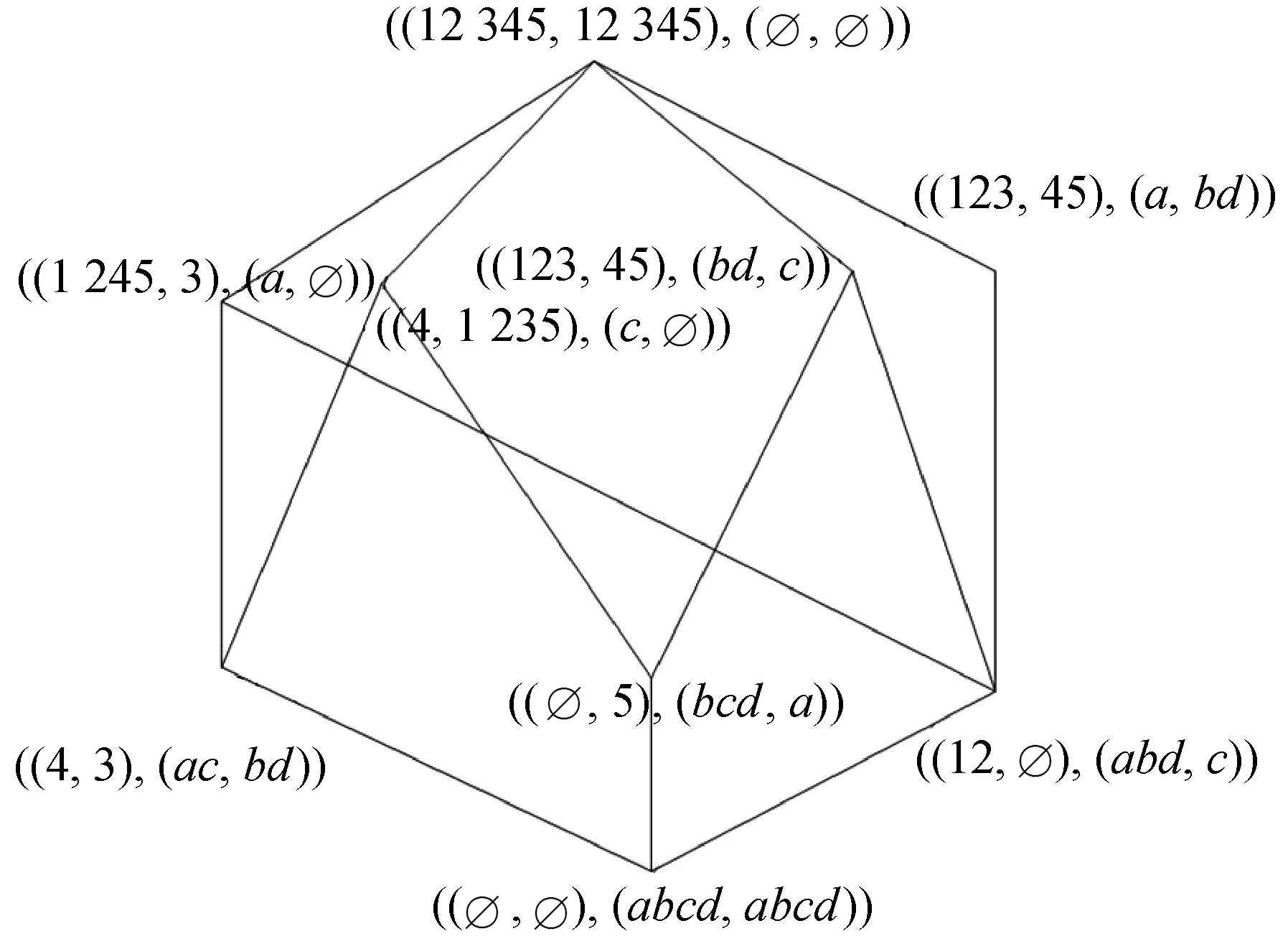
图5 AOEL(U，M，R)

根据基于属性为主和基于对象为主的三支概念格合并定义条件，在AEL(U，M，R)和OEL(U，M，R)中可能会存在一些概念，因不符合合并定义条件，在合并后的概念格中，不存在这样的概念，如例1的OEL(U，M，R)中的概念(125，(a，c))。

3 合并前后三支概念格及经典概念格之间的关系

在此先说明AOEL(U，M，R)与AEL(U，M，R)的关系，记：

定理3设(U，M，R)为形式背景，(U,M,Rc)为其补背景，其中Rc=U×MR，则下列式子成立：

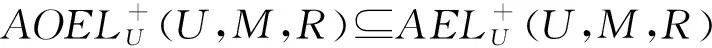
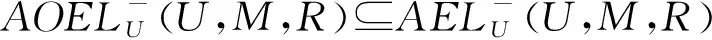
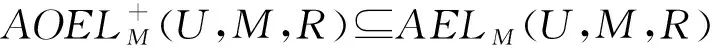
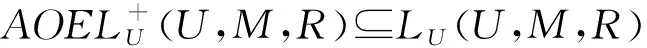
同理可证得②和③成立。

而由定理2、①、②可证得④和⑤成立。

同样对于合并后的三支概念格OAEL(U，M，R)与合并前的三支概念格的关系有以下结论成立，在此记：

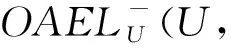
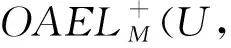
定理4设(U，M，R)为形式背景，(U,M,Rc)为其补背景，其中Rc=U×MR，则下列式子成立：

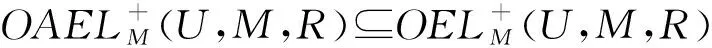
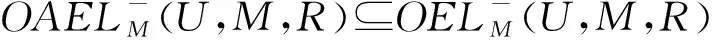
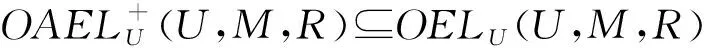
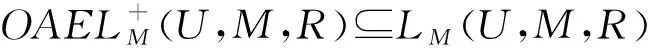
同理可证得②和③成立。

而由定理1、①、②可证得④和⑤成立。

上面两个定理说明了合并后的概念格和合并前的三支概念格及经典概念格之间的关系，下面研究合并后的三支概念格之间的关系。

定理5设(U，M，R)为形式背景，AOEL(U，M，R)为基于属性为主的三支概念格合并所得的三支概念格，OAEL(U，M，R)为基于对象为主的三支概念格合并所得的三支概念格，则对于任意((X，Y)，(A，B))∈AOEL(U，M，R)，有((X，Y)，(A，B))∈OAEL(U，M，R)或者((Y，X)，(B，A))∈OAEL(U，M，R)。

证明：∀((X,Y),(A,B))∈AOEL(U,M,R)，则由定义8知，((X，Y)，(A，B))满足下列两个条件之一:

条件1：(X,Y)≥=A且A≤=(X,Y)，X≤=(A,B)且(A,B)≥=X，

条件2：(X,Y)≥=A且A≤=(X,Y)，Y≤=(B,A)且(B,A)≥=Y。

若满足条件1，则由定义9易知，((X，Y)，(A，B))∈OAEL(U，M，R)。

若满足条件2，由将X与Y互换，A与B互换，那么((X，Y)，(A，B))就变成((Y，X)，(B，A))，同样条件将(X,Y)≥=A且A≤=(X,Y)，Y≤=(B,A)且(B,A)≥=Y也做出相应的变化得到X≤=(A,B)且(A,B)≥=X，B≤=(Y,X)且(Y,X)≥=B，则根据定义9知((Y，X)，(B，A))∈OAEL(U，M，R)。证毕。

由定理5可知，AOEL(U，M，R)和OAEL(U，M，R)中的概念数应该相等，而本文中AOEL(U，M，R)比OAEL(U，M，R)中的概念要少一个，这是因为((4，3)，ac)∈AEL(U，M，R)，(4，(ac，bd))∈OEL(U，M，R)，根据定义8生成的属性/对象概念是((4，3)，(ac，bd))；而((4，3)，ac)∈AEL(U，M，R)，(3，(bd，ac))∈OEL(U，M，R)，按照定义8生成的三支概念也是((4，3)，(ac，bd))，所以AOEL(U，M，R)和OAEL(U，M，R)中的概念数可能是不相等的。

4 三支概念格的合并算法

合并算法流程如下：

输入：由属性导出的三支概念格AEL(U，M，R)和由对象导出的三支概念格OEL(U，M，R)。

输出：由基于属性为主的三支概念格合并的三支概念格AOEL(U，M，R)和由基于对象为主的三支概念格合并的三支概念格OAEL(U，M，R)。

1.AOEL(U，M，R)={}，OAEL(U，M，R)={}

2.for(i=1；i≤m,i++)

/*m表示AEL(U，M，R)中的概念个数*/

3.{for(j=1；j≤k;j++)

/*k表示OEL(U，M，R)中的概念个数*/

4.{ if

((Xi,Yi)≥=Ai&&Ai≤=(Xi,Yi)&&Xi≤=(Ai,Bj)&&(Ai,Bj)≥=Xi≤)

{AOEL(U，M，R)=AOEL(U，M，R)∪((Xi,Yi),(Ai,Bj))

OAEL(U，M，R)=OAEL(U，M，R)∪((Xi,Yi),(Ai,Bj))}

5.elseif

((Xi,Yi)≥=Ai&&Ai≤=(Xi,Yi)&&Yi≤=(Bj,Ai)&&(Bj,Ai)≥=Yi)

{AOEL(U，M，R)=AOEL(U，M，R)∪{((Xi,Yi),(Ai,Bj))

OAEL(U，M，R)=OAEL(U，M，R)∪((Yi,Xi),(Bj,Ai))}

/*根据定理5生成OAEL(U，M，R)*/}

6.for(i=1；i≤s-1；i++)

/*s表示AOEL(U，M，R)中的概念个数*/

7.for(j=i+1；j≤s；j++)

8.if((Xi,Yi),(Ai,Bi))=((Xj,Yj),(Aj,Bj))则删除概念((Xj,Yj),(Aj,Bj))

9. 同样的方法删除OAEL(U，M，R)中的相同概念。

该算法中的第1行-第5行是根据定义8和定理5生成AOEL(U，M，R)和OAEL(U，M，R)，而第6行-第9行是分别删除AOEL(U，M，R)和OAEL(U，M，R)中相同概念。算法的时间复杂度主要体现在AOEL(U，M，R)和OAEL(U，M，R)生成和删除AOEL(U，M，R)和OAEL(U，M，R)中相同概念时，根据算法描述，AOEL(U，M，R)和OAEL(U，M，R)生成时的时间复杂度为O(mk)，而删除AOEL(U，M，R)和OAEL(U，M，R)相同概念的时间复杂度为O(s2)，如果设n=max(m，k，s)，n为m、k、s中的最大值，则本文算法的时间复杂度为O(n2)。

5 结 语

三支概念格是将经典概念格理论和三支决策理论相结合而发展起来，它使得形式概念分析更具体、更完善，而随着大数据和计算机网络的快速发展，需要对多个形式背景进行合并处理。因此，本文提出基于属性为主的三支概念格的合并和基于对象为主的三支概念格的合并的定义，并给出合并后三支概念格的性质，也就是合并后的三支概念格与合并前的三支概念格及经典概念格之间的关系，以及对两种方法合并后的三支概念格之间的关系进行了研究，在此基础上给出三支概念格合并算法，并通过实例验证本文提出的理论。后续将对合并后的三支概念格的属性约简做更深入的研究。