基于长度信息和深度卷积神经网络分类建模的蛋白质二级结构预测方法
2021-11-15朱树平刘毅慧
朱树平 刘毅慧
(齐鲁工业大学(山东省科学院)计算机科学与技术学院 山东 济南 250353)
0 引 言
蛋白质二级结构预测是预测三维结构的基础,而三维结构的盘旋所形成的构象将决定其发挥的生物学功能,因此确定蛋白质二级结构将对研究人体内蛋白复合物以及医学疾病的防治有很大的帮助。二级结构的预测可以从输入特征和预测方法方面改进,除了基于氨基酸本身特征之外,很多其他的特征也被引入二级结构的预测中,如:基于非担保残余能量构建自相关方程、功能域、复杂性度量因子和位置特异性差分矩阵(Position specific scoring matrix,PSSM)等[1]。主要方法有支持向量机(Support vector machine,SVM)[2-4]、深度学习[5-6]、隐马尔可夫模型[7]、贝叶斯算法[8-9]、K最近邻[10]和模糊聚类[11]等。
近年来,通过结合不同的特征和不同的方法,准确率获得不断的提高,可达到80%,其中,深度学习方法表现出很好的预测性能。文献[12]采用长短期记忆双向循环神经网络(LSTM-BRNN)的模型来捕获蛋白质氨基酸之间的非局部相互作用,预测蛋白质二级结构的Q3准确率接近84%。文献[13]将氨基酸的物理化学特性、HHBlits特征和PSI-Blast特征结合为一个58位的特征,作为一种名为深度起始-内部-起始(Deep3I)网络的输入特征,建立了在线预测服务器,在预测蛋白质二级结构方面取得了较好的结果。在文献[14]也提及今后对蛋白质二级结构预测的方向应当从大数据、模板的使用和深度学习的方向进行。文献[15]采用基于数据划分和半随机子空间的方法预测蛋白质二级结构,在25PDB和CASP类上都取得了超过80%的准确率。基于此基础,本文首先选取了大数据集Astral[16]和cullPDB[17]组成的15 666条蛋白质作为训练集,按照蛋白质长度将其划分为4组;然后在每一组数据上,都使用深度卷积神经网络调整超参数进行实验;最后得到4个最佳的独立预测模型块,进而又将这4个模型块组合成一个整体网络模型(称为LIM-DCNN4)。模型建好后,使用CASP类数据和CB513数据进行测试,在测试过程中,测试集中每一条蛋白质会根据自己的长度,选择合适的模型块进行预测,最终得到整个数据集的预测结果。为了使实验结论更加充分,又按照相同的原理,将测试集划分为6段并进行实验,得到6分段的模型(称为LIM-DCNN6)。实验结果表明,适当增加划分段数,对于提升预测准确率是有效的,因为它能让蛋白质更好地选择与其局部信息相似度高的模型进行预测,并且本文设计的LIM-DCNN模型也得到了较优的CB513准确率。
1 数据和模型
1.1 数据和特征选择
获取蛋白质结构常用的数据库是蛋白质数据库(PDB),但在该数据库中存在着许多具有相似序列和结构的数据,这样就为蛋白质结构的划分带来很多困难。为了能够解决该问题,产生了蛋白质结构分类(SCOPe)数据库。它是根据蛋白质结构和进化关系从层次结构中的大多数已知结构的蛋白质手动策划的域的排序,并且它也是唯一一个手工标识蛋白质不同层次关系和定义域的数据库,包含了超过65%的PDB中的结构[18]。本文中使用的ASTRAL数据是从SCOP数据库中选取出来的,实验时使用了6 892条蛋白质,除此之外还选择了CullPDB数据,两者在实验中合称为AstraCull,共15 666条蛋白质。对于测试集,本文基于蛋白质同源相似度低于25%,选择了CASP9[19]、CASP10[20]、CASP11[21]、CASP12[22]和CB513[23]数据,具体的实验数据如表1所示。

表1 测试和训练数据表
在实验中,对于蛋白质特征选取了20位的PSSM矩阵,它是由PSI-BLAST多序列比对技术产生。通过PSI-Blast设置特定的收敛参数e-value为0.001,进行3次迭代,使用BlOSUM62作为氨基酸替换矩阵得到的,它存储了每个位置上所有氨基酸的保留分数,能够很好地捕捉长短距离信息特性[24]。为了捕获更多蛋白质的局部信息,对于该特征进一步处理,设滑动窗口数为13,此时假设一条蛋白质长度为L,则每条蛋白质都会按照自身长度将特征设置为20×13×L,本文以该特征作为神经网络的输入。
1.2 模型建立过程
氨基酸序列的折叠构像决定了蛋白质的二级结构,而氨基酸序列的折叠构像在一定程度上受序列长度的影响。因此本文主要是按照蛋白质长度对数据进行划分,然后调整深度卷积神经网络超参数,寻找参数最优值建立模型的过程。该模型能够让蛋白质选择与其长度相近的模型进行预测,从而提高了预测的准确率。
1.2.1数据划分
首先把上文中提及的所有数据集按照蛋白质长度划分为i组,每组的数据为Di。4分段按照长度介于0到150、150到250、250到350和350以上划分,划分后的蛋白质数据分别可以表示为D1={B|0

表2 LIM-DCNN4蛋白质条数数据表

表3 LIM-DCNN4氨基酸个数数据表
为使实验结果更加充分,又按照长度介于0到100、100到200、200到300、300到400、400到500和500以上划分为6组后,同理,每组数据可以表示为:D1={B|0
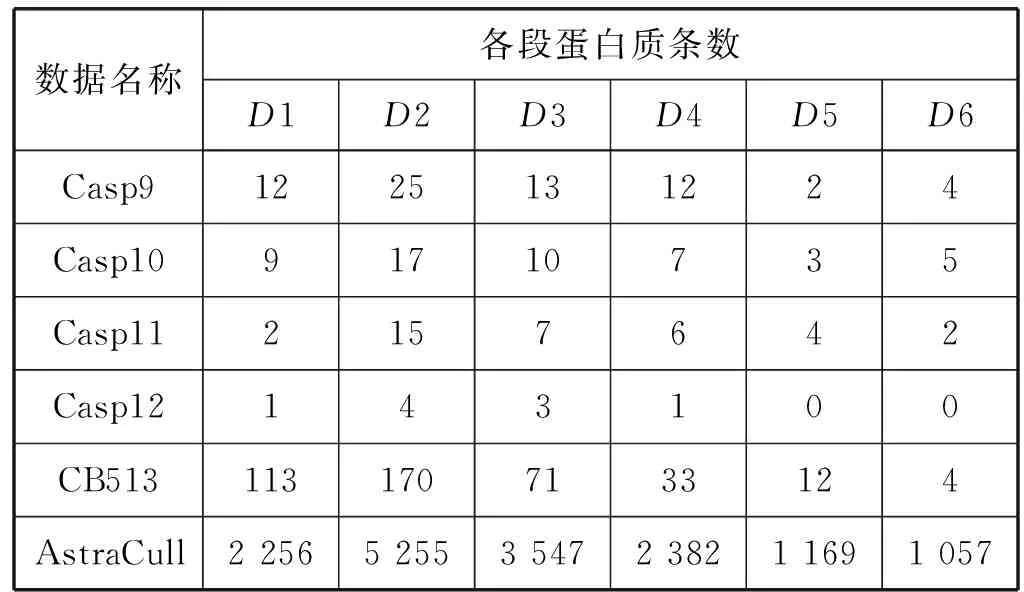
表4 LIM-DCNN6蛋白质条数数据表
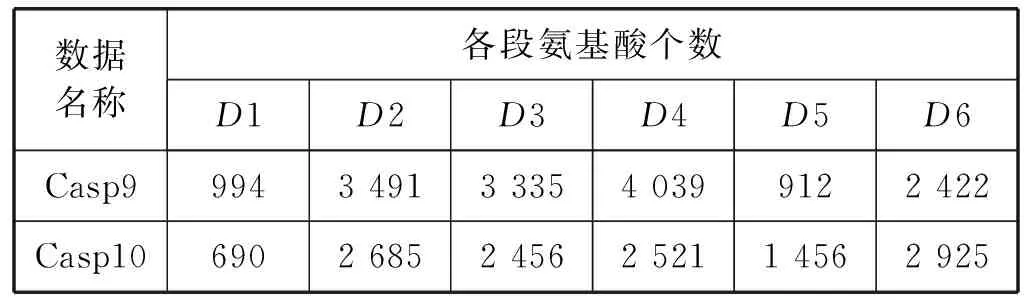
表5 LIM-DCNN6氨基酸个数数据表

续表5
1.2.2深度卷积网络建模
对于4分段的模型,使用表2中AstraCull的D1、D2、D3和D4数据,建立LIM-DCNN4模型;对于6分段模型,使用表4中AstraCull的D1、D2、D3、D4、D5和D6数据,建立LIM-DCNN6模型。下面以4分段为例进行说明:若假设每一个数据集中,氨基酸的个数为ni,输入特征矩阵为P(i),标签矩阵为T(i),则有:
(1)
(2)

若用model代表DCNN建模过程,则该过程可以表示为:
Mi=model(P(i),T(i))
(3)
以D1段为例,第一段数据的输入P(1)具体值为:
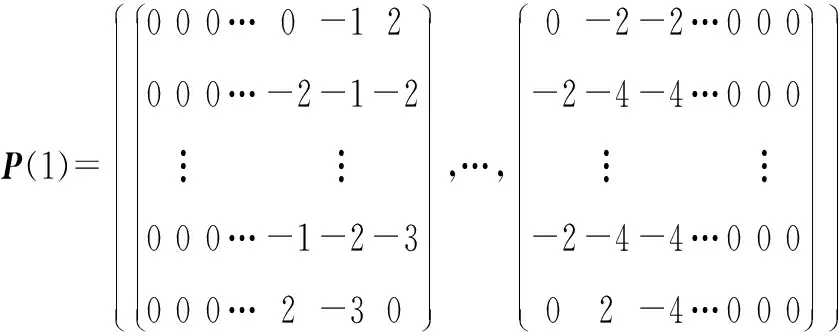
第一段数据标签T(1)的具体值为:
T(1)=(1,…,1)(1,527 862)
第一段数据模型M1可以表示为:
M1=model(P(1),T(1))
其余三段可以根据类似的原理依次得到。该过程如图1所示。
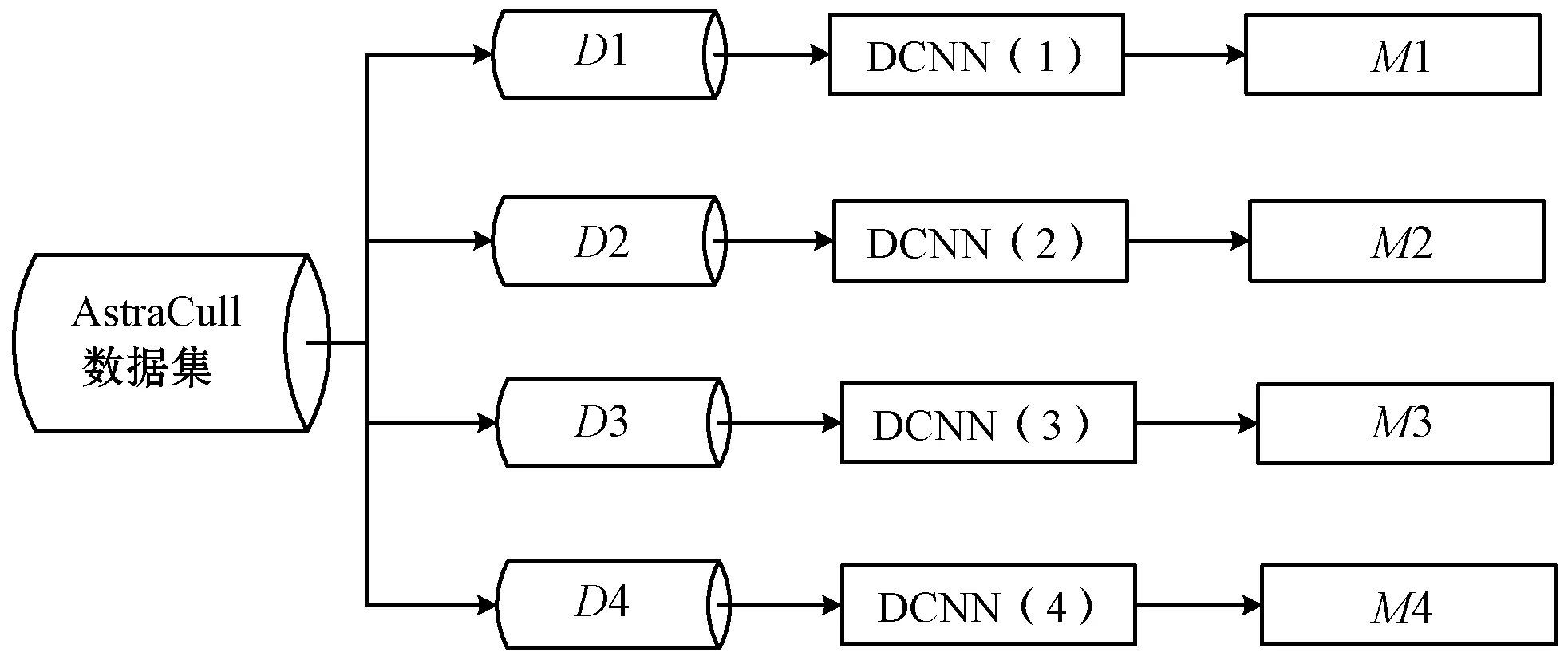
图1 LIM-DCNN4建模过程图
具体而言对于一个20×13的特征矩阵,通过实验得到,它在图1中DCNN具体过程如图2所示。

图2 DCNN过程
(4)
式中:e、f为输入特征矩阵的行和列;u、v为卷积核的行和列下标;b代表偏置;φ为激活函数;K代表第t层的卷积核;k代表卷积核的大小。实验中使用的是线性整流激活函数(ReLU)。
在反向传播的过程中,为保证获得的训练模型要做的就是最小化损失函数ψ。寻求误差的表达式用损失函数对卷积核和偏置求偏导数,ψ对卷积核的偏导符合式(5),ψ对偏置的偏导符合式(6)。
(5)
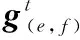
(6)
(7)
得到误差项以后,便可以计算权值W,权值的更新计算符合以下公式:
W←W+α×θ(e,f)×X(e,f)
(8)
式中:α代表学习率;“←”代表左边数值随右边数值的变化进行更新。
为了防止过拟合,在损失函数中加入了正则化因子λ,加入正则化因子后的损失函数ψ可以表示为:
(9)
在实验中选择25PDB[25]数据作为调参数据,基于超参数的取值范围,依次给定合理的卷积核大小、卷积核个数、学习率和正则化大小等范围,然后使用随机梯度下降算法,寻找每个范围内,上述超参数实验结果具体的最佳值,从而得到最优的网络模型。
1.3 测试过程
上述4个模型建好以后,使用Casp9、Casp10、Casp11和CB513进行测试。可以有两种方法测试:一是不对测试集数据进行划分,让蛋白质逐条进行测试;二是先对测试数据集的蛋白质划分再测试。
1) 测试一 测试数据中的蛋白质依次进入到LIM-DCNN4模型中,根据自身长度选择模型进行测试,此时假设一条长度为L的蛋白质,在进入LIM-DCNN4模型时的特征矩阵为B,输出为Y,则有:
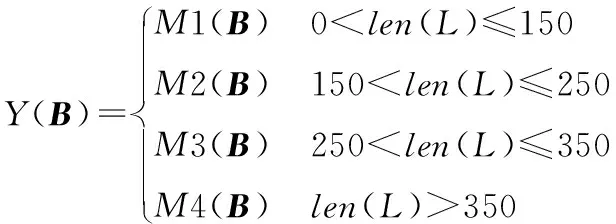
(10)
式中:M1、M2、M3和M4分别代表LIM-DCNN4中每个模型的测试过程;B为20×13×L的矩阵;len(B)代表计算蛋白质的长度;该过程如图3所示。
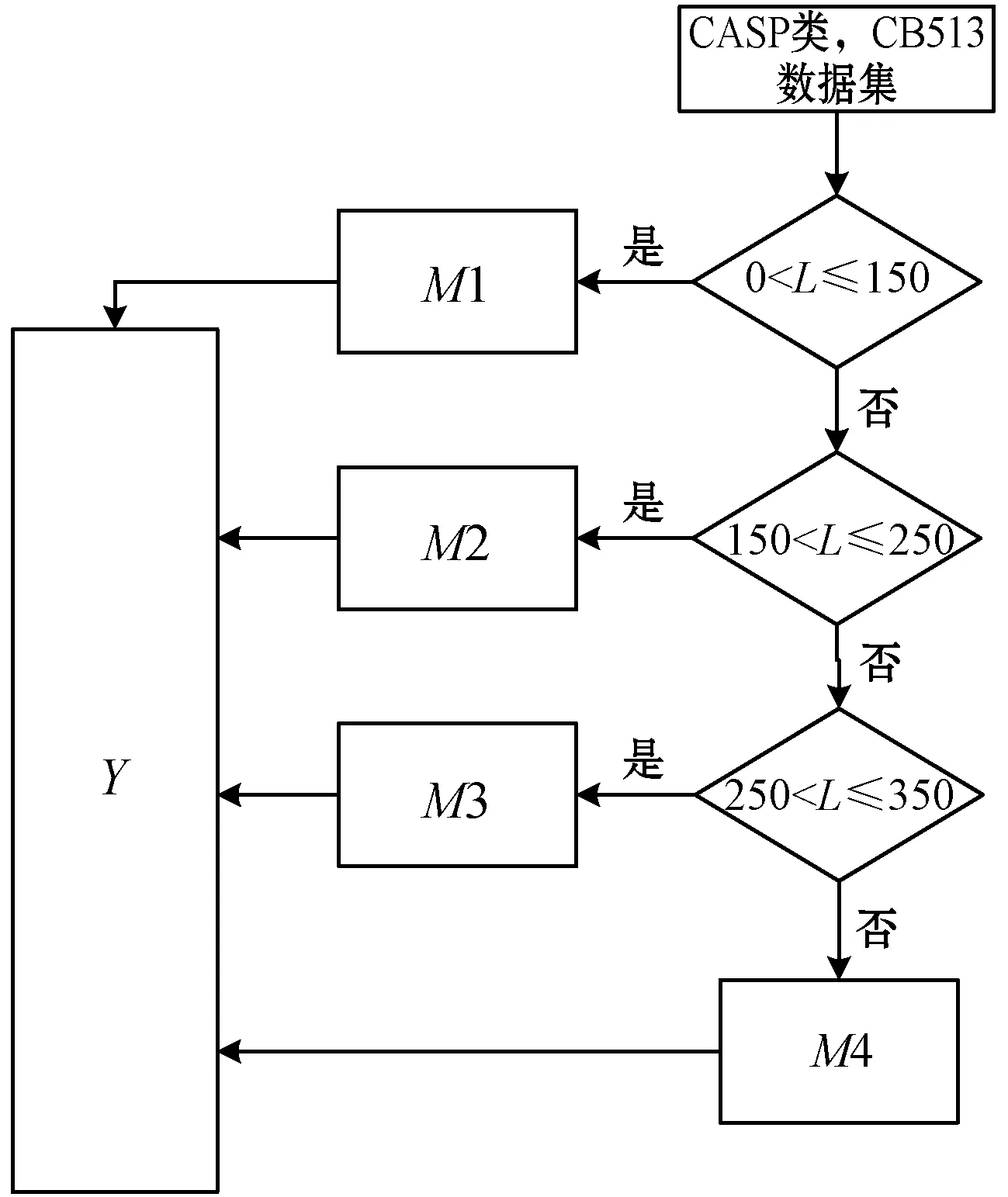
图3 LIM-DCNN4测试流程图(1)
2) 测试二 先将测试数据进行划分,然后把每一段的数据分别放在对应模型上进行测试,最后把结果整合起来。CASP类和CB513数据分组后分别对应表2中的D1、D2、D3和D4数据,提取每一个数据中的特征矩阵P(1)、P(2)、P(3)和P(4),它们的含义与式(1)相同,都是特征20×13×ni的矩阵,此时ni代表测试集中每一段氨基酸的个数,即表3数据。P(1)、P(2)、P(3)和P(4)分别会选择M1、M2、M3和M4进行预测,得到测试集中n条蛋白质的输出结果Y,该过程表示为:

(11)
Y=Y1∪Y2∪Y3∪Y4
(12)
式中:M1、M2、M3和M4分别代表LIM-DCNN4中每个模型的测试过程;Y1、Y2、Y3和Y4分别代表每一部分的测试结果;Y是将测试结果求并集得到的1×L的矩阵,Y∈{C,H,E}。该测试过程如图4所示。

图4 LIM-DCNN4测试流程图(2)
最后将实验得到预测结果与数据集中的正确标签结果相比较得到了预测准确率。这两种测试方法的区别在于是否先对测试集进行数据划分,不进行数据划分的直接使用总模型LIM-DCNN4预测,进行数据划分的使用单一模型M1、M2、M3和M4分别预测,两者的预测结果并无差别。对于6分段的数据,按照相同的原理进行测试即可。
2 判别标准和实验结果
实验使用判别标准是计算三态蛋白质Q3和每一类的准确率,即C类蛋白质、E类蛋白质和H类蛋白质的准确率QC、QE和QH。在进行实验的过程中,分i段可以得到i个模型,首次得到的是4分段的4个模型:M1、M2、M3和M4。另外还有6分段的6个模型:M1、M2、M3、M4、M5和M6。其次得到的是每个模型中卷积神经网络的层数和相关参数,最后得到Casp9、Casp10、Casp11、Casp12和CB513训练在4个模型上的实验结果1和在6个模型上的实验结果2。
2.1 判别标准
按照H,G,I→H,E,B→E,其他→C将一条氨基酸序列转化为H(螺旋)、E(折叠)和C(卷曲)三种形态,关于Q3、QC、QE、QH计算符合以下公式:
(13)
(14)
式中:numr()表示计算预测正确的个数;num()代表单纯计数;len(SS)表示蛋白质的长度;Z∈{C,H,E}代表三种取值情况;b代表氨基酸的下标,即num(SSb=B)计算SS符合某一类蛋白质的氨基酸个数。
2.2 模型参数
在实验过程中,使用25PDB数据作为调整参数的测试集,依次设置超参数的范围,在保证25PDB实验结果Q3准确率高的情况下,寻求超参数的最优值。以M1模型为例,学习率变化对于准确率的影响如图5所示,在学习率取值为0.003 5时25PDB的Q3准确率最高。其他模型的参数设置与上述原理相同。经过多次实验调整LIM-DCNN4和LIM-DCNN6的超参数,得到的具体超参数结果如表6和表7所示。这两个模型的区别在于由于基于不同的蛋白质长度划分,LIM-DCNN6划分得更为细致,因此每一段模型训练的时间会缩短,并且更能够让蛋白质可以选择与自己相似度更高的蛋白质进行预测,准确率会更高。但是,蛋白分段长度的选择也不是越细越好,要根据训练数据中蛋白质长度合理评估确定。

图5 学习率对M1准确率影响图像

表6 LIM-DCNN4网络模型参数

续表6
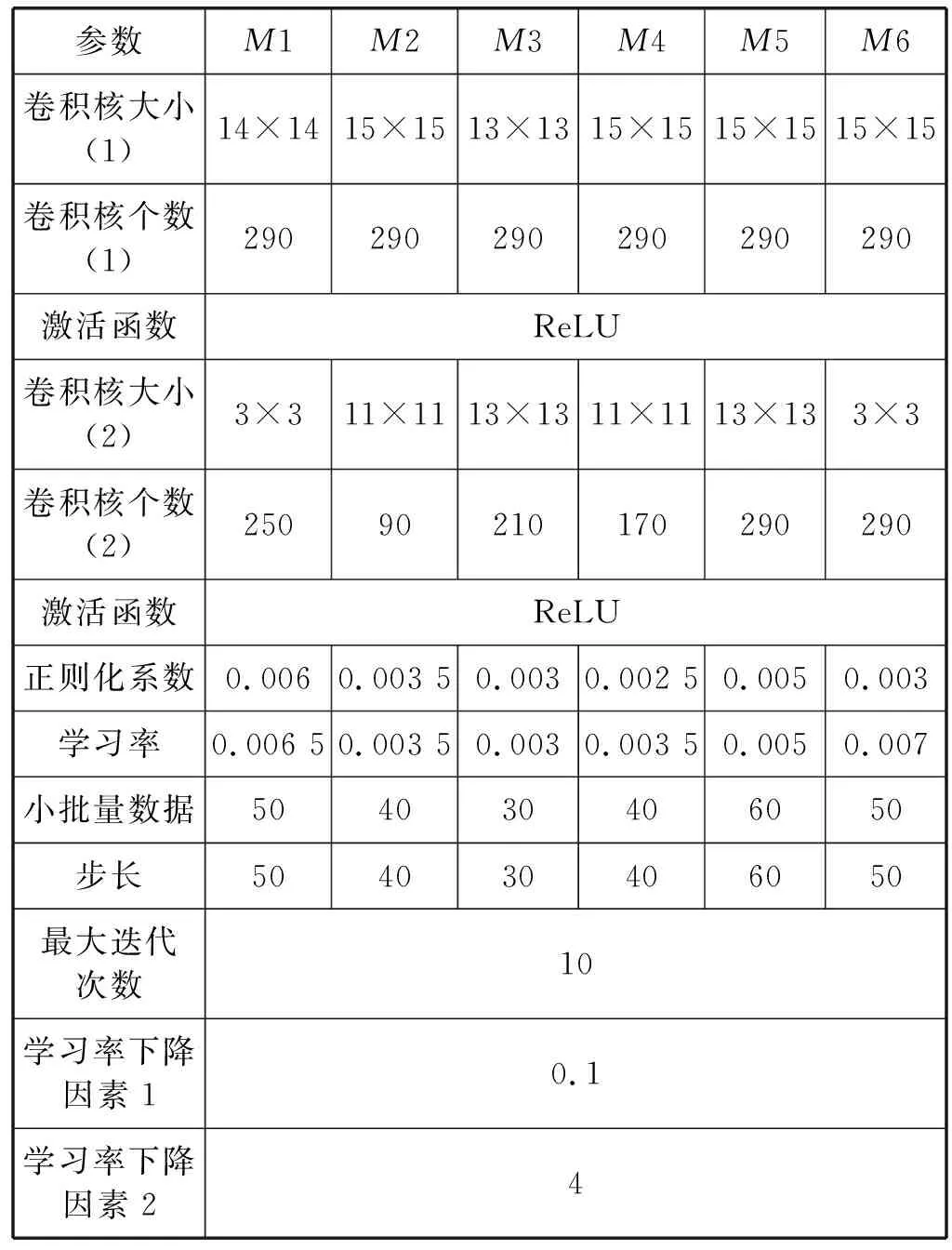
表7 LIM-DCNN6网络模型参数
在4分段模型中,如表6所示,M1中使用了3个卷积层,3个激活层,加上输入层、全连接层、Softmax层和分类输出层,共10层网络结构。其中,学习率α设置为0.003 5,正则化系数为0.005,最大迭代次数为10,每隔4次,将学习率变为α×0.1,每隔40个小批量数据进行权值的更新调整。M2、M3和M4都使用2个卷积层和2个激活层,共有8层网络结构。对于M2,其学习率α设置为0.007,正则化系数为0.003,最大迭代次数为10,每隔8次,将学习率变为α×0.1,每隔80个小批量数据进行权值的更新调整;对于M3,其学习率α设置为0.005 5,正则化系数为0.002 5,最大迭代次数为10,每隔3次,将学习率变为α×0.1,每隔30个小批量数据进行权值的更新调整;对于M4,其学习率α设置为0.005 5,正则化系数为0.003 5,最大迭代次数为10,每隔3次,将学习率变为α×0.1,每隔30个小批量数据进行权值的更新调整。
在6分段模型中,如表7所示,预测模型M1、M2、M3、M4、M5和M6都使用2个卷积层,2个激活层,加上输入层、全连接层、Softmax层和分类输出层,共8层网络结构。所有模型的最大迭代次数为10,每隔4次,将学习率变为α×0.1。对于M1学习率α设置为0.006 5,正则化系数为0.006,每隔50个小批量数据进行权值的更新调整;对于M2学习率α设置为0.003 5,正则化系数为0.003 5,每隔40个小批量数据进行权值的更新调整;对于M3学习率α设置为0.003,正则化系数为0.003,每隔30个小批量数据进行权值的更新调整;对于M4学习率α设置为0.003 5,正则化系数为0.002 5,每隔40个小批量数据进行权值的更新调整;对于M5学习率α设置为0.005,正则化系数为0.005,每隔60个小批量数据进行权值的更新调整;对于M6学习率α设置为0.007,正则化系数为0.003,每隔50个小批量数据进行权值的更新调整。
2.3 实验测试结果
得到上述2个大的深度卷积网络结构模型后,分别使用Casp9、Casp10、Casp11、Casp12和CB513进行测试。4分段网络模型LIM-DCNN4得到的实验结果如表8所示,6分段网络模型LIM-DCNN6得到的实验结果如表9所示。
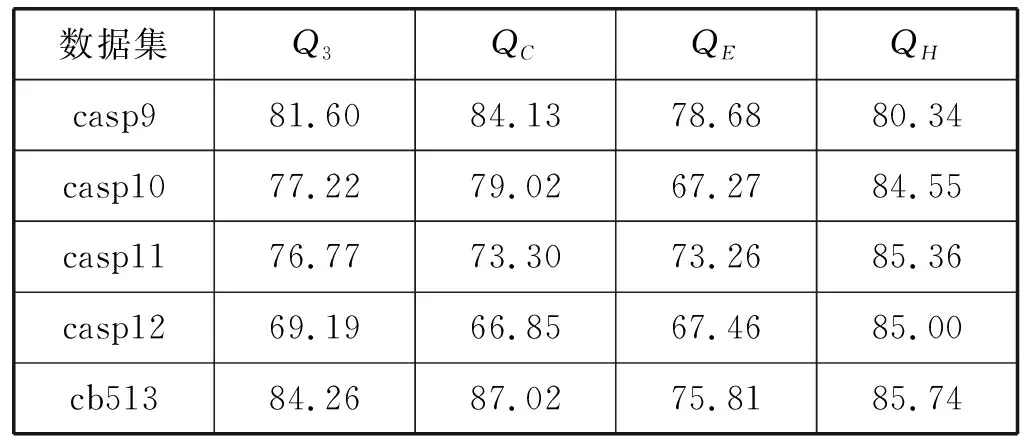
表8 LIM-DCNN4实验结果(%)
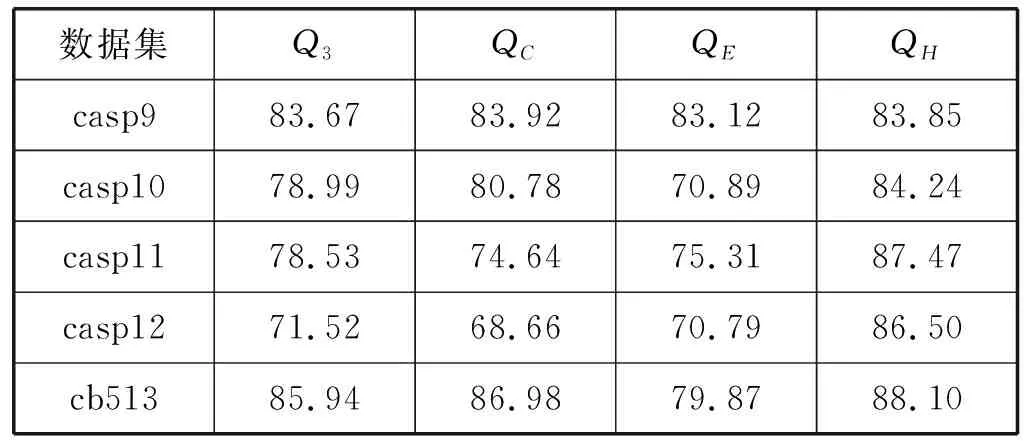
表9 LIM-DCNN6实验结果(%)
可以明显看到,任何数据集6分段的Q3准确率都比4分段要高很多,说明了依据蛋白质长度划分数据进行预测的有效性。这是因为,在合理范围内划分数据段越细致,越能够考虑到蛋白质本身的序列特点和长短距离信息,从而能让蛋白质更好地选择适合自身的预测模型,进而能达到更好的预测效果。
本文设计的LIM-DCNN6方法与使用两个阶段神经网络的PSIPRED[26]方法、使用非冗余蛋白质数据库训练的两层反馈神经网络的PHD Expert[27]方法、使用神经网络和线性判别分类器设计网络模型的Prof[28]方法,使用双轨隐马尔可夫模型的SAM[29]方法、使用JNet算法结合隐马尔可夫模型进行7倍交叉验证的Jpred[30]方法、使用相关序列对预测的序列的局部成对比对的Predator[31]方法、使用内部认知机制(KDTICM)理论建立复合金字塔的CPM[32]方法、使用双向朴素神经网络的SSpro(without template)[33]方法、使用迭代地将二级结构预测与溶剂可及性和主链扭转角的预测耦合起来以开发多步神经网络算法的SPINE-X[34]方法、使用条件随机场的RaptorX-SS8[35]方法、使用条件随机场和浅层神经网络组合为深度卷积场的DeepCNF-SS[36]、使用小波提取特征和支持向量机建模的6GTPCs[37]方法和使用卷积和长短期记忆神经网络的NetSurf-2.0[38]方法和使用长短期记忆双向递归神经网络的SPIDER[39]方法,上述各类相比较的实验结果如表10所示。
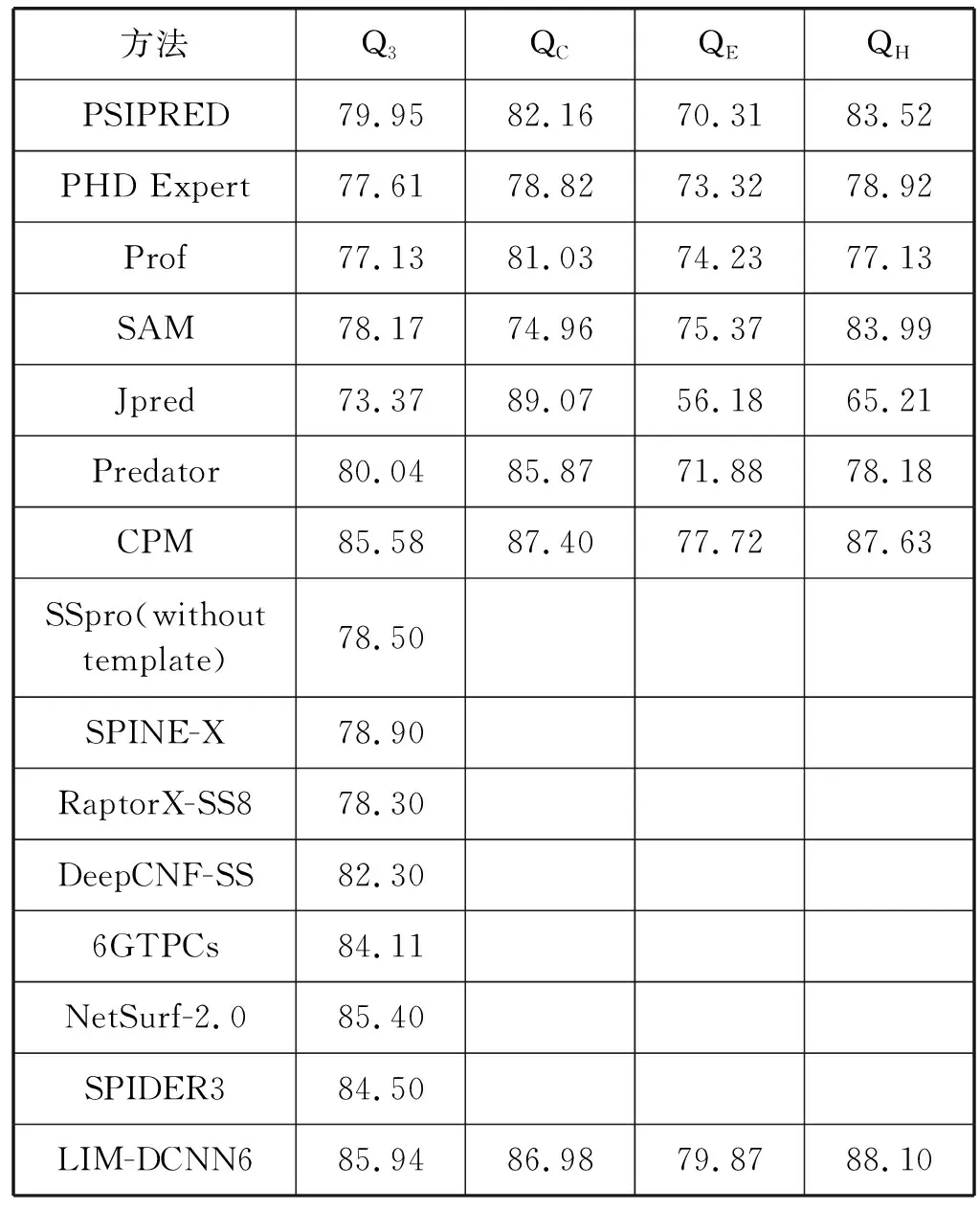
表10 实验结果比较表(%)
可以看出,本文建立的LIM-DCNN6模型,预测CB513的Q3、QC、QE和QH准确率,除了QC低于CPM的87.40%之外,其余都取得了最好的预测效果,说明了基于蛋白质长度和深度卷积神经网络分类建模是有效的。
3 结 语
本文提出基于蛋白质长度划分数据并使用深度卷积神经网络(LIM-DCNN)分类建模的蛋白质二级结构预测方法,取得了较好的预测效果。通过实验得到了两种不同的预测模型:LIM-DCNN4和LIM-DCNN6,两个模型都是基于蛋白质长度进行划分后建立的,这种分段的方法能够很好地缩短模型训练的时间。LIM-DCNN6结果比LIM-DCNN4结果好的原因是在合适范围内增加分段数,能够使蛋白质更好地选择与其长度相近的蛋白质进预测。LIM-DCNN模型优于其他经典模型的原因在于它使用了大数据、模板和深度学习方法,这也就为下一步蛋白质二级结构预测的研究进一步指明了方向。当然,后续的工作也可以通过设置不同的滑动窗口,来获得更具体的蛋白质特征,或者结合其他深度学习的方法来实现预测,有望能够进一步提升蛋白质二级结构预测的准确率。
