基于改进多目标HQPSOGA求解武器目标分配问题

邱少明 冯江惠 杜秀丽 王建伟

(大连大学通信与网络重点实验室 辽宁 大连 116622)

0 引 言

武器-目标分配问题(Weapon Target Assignment, WTA)提供武器资源的分配方案，是一种非确定性多项式(Non-deterministic Polynomial, NP)完全问题，目前重点研究多个判别标准下求解最优分配方案的问题，因此常看作多目标优化问题(Multi-objective Optimization Problem, MOP)。启发式随机搜索智能优化算法，如粒子群算法(Particle Swarm Optimization, PSO)[1]、蚁群算法[2]和差分进化算法[3]等极大地提高了WTA求解效率。PSO及其派生算法在WTA的研究主要从求解效率和解的质量两方面展开，文献[4]根据超鞅收敛定理证明静态粒子群优化算法(Static Particle Swarm Optimization, SPSO)的收敛性在概率上达到全局最优，且量子行为粒子群算法(Quantum-behaved Particle Swarm Optimization, QPSO)也是一种全局收敛算法。Clerc等[5]、Kadirkamanathan等[6]和Cleghorn等[7]给出稳定收敛时加速因子的取值范围，丰富了PSO的理论研究。

目前PSO的应用研究更丰富，算法迭代中种群的多样性求解质量好坏是重要衡量指标。基于此，文献[8]提出一种“反向预测器”资源规划粒子群算法，迭代时将粒子位置进行扰动，增加粒子多样性；文献[9]提出的算法中，设置程序挑选引导粒子更新种群，保证算法多样性和快速收敛性。近年来，量子计算为智能计算的优化提供了新思路，孙俊[10]提出基于δ势阱的QPSO，给出描述量子空间中粒子行为的量子模型，粒子具有更强的不确定性；针对QPSO的早熟收敛现象，提出多样性控制的QPSO；文献[11]根据聚集度判断早熟停滞，并用慢变函数克服早熟收敛,保持了种群多样性；文献[12]针对QPSO粒子间信息共享机制单一等问题，利用社会学习策略和莱维飞行策略提高算法的收敛精度和速度。在多目标QPSO方面，文献[13]将QPSO与遗传算法(Genetic Algorithm, GA)相结合，提出混合量子行为粒子群和可调节遗传算法(Hybrid Quantum-behaved Particle Swarm Optimization and self-adjustable Genetic Algorithm, HQPSOGA)，作用于雷达干扰资源优化多目标分配模型，为干扰机的形成提供了更好的整体干扰能力。但是QPSO在求解多目标优化问题时，收敛速度快也易过早丧失解的多样性，陷入早熟收敛[14]。

本文首先引入一种多样性判别方法，提出粒子多样性贡献度的概念，基于随机选择的聚类算法(CLARANS)和模糊贴近度原则，从目标函数和决策空间两个角度综合度量粒子间相似性，从而判别粒子多样性贡献度。该方法用于HQPSOGA的QPSO部分，根据粒子多样性贡献度和适应度值比较随机新增粒子与旧有粒子的优劣并更新个体最优解，最终引导粒子找到Pareto最优解。HQPSOGA充分利用了QPSO和可调节遗传算法(Adjustable Genetic Algorithm, AGA)在寻找全局最优解上的优势，在解决方案质量、稳定性、收敛速度和可信度方面具有更优越的性能[13]，因此提出基于多样性贡献度的HQPSOGA(Diversity Contribution Improved HQPSOGA, DCI-HQPSOGA)，在QPSO部分引入多样性判别，通过性能测试函数，可更直观地展现所提方法对QPSO与HQPSOGA求解质量及种群多样性的影响，便于对比分析。最后，改进算法应用于两目标模型下的静态武器-目标分配问题(Static Weapon Target Assignment, SWTA)，提升战场环境下的求解精度。

1 相关理论

1.1 多目标优化问题

MOP由一组目标函数和约束组成，数学描述如下：

(1)

s.t.gi(X)≤0i=1,2,…,p

式中：X=(x1,x2,…,xn)T是Rn空间的n维向量。X所在空间Ω是问题的决策空间，当且仅当所有目标上的决策向量X1不比另一个决策向量X2差时，叫作X1支配X2；fi(X),i=1,2,…,m为问题的子目标函数，各子目标间相互冲突，即不存在X∈Ω使f1(X),f2(X),…,fm(X)在X处同时取最小值，这样的折中解的集合叫作Pareto最优解集、非劣解集或非支配解集；m维向量(f1(X),f2(X),…,fm(X))所在空间为问题的目标空间，gi(X)≤0,i=1,2,…,p为约束函数；所有Pareto最优解组成的曲面为Pareto前沿。

1.2 基于随机选择的聚类算法

CLARANS算法是大型应用聚类算法(Clustering LARge Applications, CLARA)和k-中心点聚类算法(Partitioning Around Medoid, PAM)的结合，该算法选择数据的小部分作为样本，可拓展数据处理量的伸缩范围，提高聚类效率，在一定程度上克服了K-means聚类算法对“噪声”数据敏感以及模糊聚类算法求解效率低的问题，也避免了密度聚类算法DBSCAN需调整参数带来的高计算复杂度。

CLARANS的基本流程：随机选k个对象作为聚类中心，剩余对象就近分配给对应聚类中心，得到k个簇，聚类中心随着迭代进行更改：在每个簇中，随机选一个非聚类中心点，计算该点与其他点的距离之和，如果该和比当前聚类中心与其他点的距离之和小，则该点作为新聚类中心，继续迭代直到随机选择的次数满足要求为止。

1.3 模糊贴近度原则

模糊贴近度在模糊模式识别中描述两个模糊集的接近程度，贴近度越大接近程度越大。文献[15]采用贴近度识别发信号的雷达，采用特征参数集的标准差反映特征参数的影响程度。本文模式识别的聚类过程采用CLARANS，用模糊距离贴近度计算簇中粒子到聚类中心的接近程度[16]，聚类中心即已知模型，其他粒子与聚类中心的距离贴近度即两个模型的相似度。欧氏距离和余弦距离等相似度计算公式不适用于粒子决策空间维数较多的情况，且不能表示粒子在决策空间中各维度的相似性。

2 基于多样性贡献度的混合量子行为粒子群和可调节遗传算法

2.1 量子行为粒子群算法

QPSO以更多样化的方式重新定义PSO中粒子的位置和速度[17]，算法假设在局部吸引点的每个维度上存在一维δ势阱，且种群中每个粒子都具有量子行为，粒子的量子态由波函数描述。粒子的位置由蒙特卡罗模拟方法更新如下：

(2)

2.2 DCI-HQPSOGA及求解步骤

DCI-HQPSOGA在HQPSOGA的基础上改进，在粒子群位置更新后加入本文的多样性判别方法，程序流程如图1所示。本文所指算法均为多目标算法，改进的QPSO部分记为DCI-QPSO。

图1 DCI-HQPSOGA流程

2.3 DCI-HQPSOGA具体实现

多样性贡献度的计算分两步：第一步，先用CLARANS将粒子分为k类，计算粒子与聚类中心的距离，作为粒子的第一部分多样性贡献度。距离越小，相似性越大，多样性贡献度越小。CLARANS聚类过程中，k为当前非劣解个数，每个非劣解代表一个多样性的方向，为找到多个多样性的方向，用非劣解初始化各聚类中心，使得每个多样性方向上相似性大的粒子归为一簇。

从簇中随机选择非当前点，更新聚类中心，为平衡解的质量和求解效率，用参数δ计算每个簇中选择聚类中心的次数tRand，计算式表示为：

tRand=δ×cl

(3)

式中：cl表示当前簇中粒子的数量；tRand∈[1,cl]。

粒子到聚类中心的距离D计算式表示为：

(4)

式中：第一项和第二项表示粒子到聚类中心的余弦距离和欧氏距离；D即目标函数上粒子的多样性贡献度。

第二步，利用式(5)的距离贴近度计算粒子的第二部分多样性贡献度。

(5)

用第一步的聚类中心作为模型，同一个簇中的其他粒子作为待识别对象，计算结果表示粒子与聚类中心的相似程度。

综上，粒子多样性贡献度表示为：

(6)

式中：β表示两种距离所占比例，通常β=0.5。

通过综合比较多样性贡献度小的粒子与引入的随机新增粒子来改善个体最优解，先计算多样性贡献度的界限值b，计算式为：

b=(max(divContri)-min(divContri))×

(MAX_Iter-iter+1)/MAX_Iter

(7)

式中：iter是当前迭代次数;divContri是粒子多样性贡献度矩阵。b保证在增加多样性的同时，不破坏粒子向最优方向移动。记录贡献度小于b的粒子，将这些粒子组成的种群称为pop，引入随机新增粒子popR，令popR与pop的规模相等，计算两者对应位置粒子的适应度值，保留较优粒子。

3 用DCI-HQPSOGA求解SWTA问题

3.1 SWTA问题模型

在经典SWTA场景[19]下构建SWTA多目标优化数学模型：

式中：xij表示分配给目标j的第i种武器的数量。

构建两个目标函数：目标生存概率最小函数f1和武器弹药消耗最少函数f2，第i种武器对目标j的毁伤概率为pij，第i种武器打击目标j时目标j的生存概率为qij=1-pij、价值为Vj。f1计算式表示为：

(8)

式中：目标价值Vj是对战术、目标威胁度等指标的综合考量[20]。

设武器消耗量取决于武器使用个数与其对于目标的价值，则f2计算式表示为：

(9)

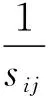
(10)

综上，SWTA模型表示为：

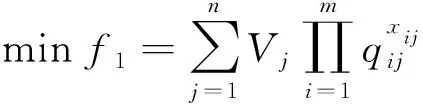
(11)

3.2 用DCI-HQPSOGA实现WTA

实现步骤参考图1，初始化参数包括武器数weaponNum、目标数Dim、毁伤概率矩阵p、DCI-HQPSOGA初始参数的设置。

4 实验与结果分析

4.1 DCI-HQPSOGA性能测试

首先，采用两目标测试函数ZDT1-ZDT4对比分析QPSO[10]、DCI-QPSO、NSGA-II、HQPSOGA和本文算法的性能，四个测试函数是两目标最小化问题，其中ZDT4具有局部最优值，干扰全局Pareto前沿的搜索，可检测算法克服陷入局部最优的能力[23]；再用GD(世代距离)、IGD(反世代距离)、HV(超体积指标)和Spacing(均匀性度量指标)检测算法收敛性和多样性，GD度量解的收敛性，Spacing度量解分布的均匀性，IGD和HV综合度量解的收敛性和多样性。多样性包括体现粒子分布均匀程度的均匀性和整个解集在目标空间中分布广泛程度的广泛性，GD、Spacing和IGD值越小越好，HV值越大越好。实验种群数和迭代次数均为100，取20次运行的最好结果，所求Pareto前沿如图2所示，四种性能指标结果如表1-表4所示。

(a) ZDT1

(b) ZDT2

(c) ZDT3

(d) ZDT4图2 五种算法在ZDT1-ZDT4上的Pareto前沿

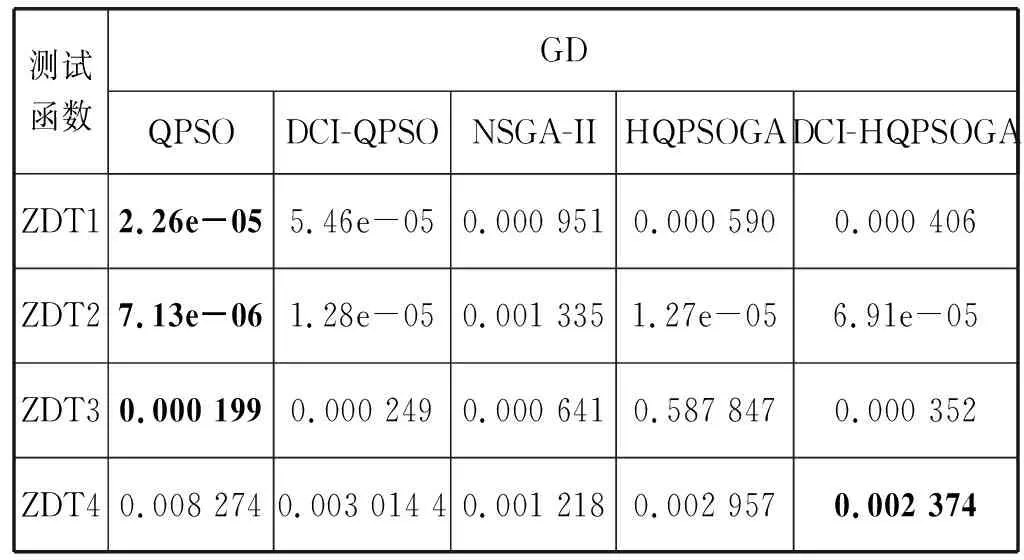
表1 五种算法在GD指标上的比较

表2 五种算法在IGD指标上的比较

表3 五种算法在HV指标上的比较

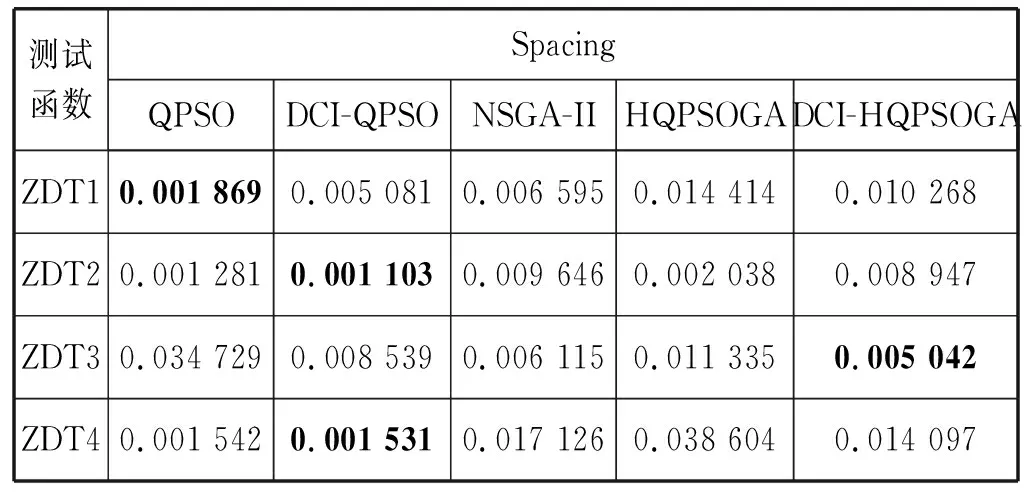
表4 五种算法在Spacing指标上的比较

对比图2可知：五种算法在ZDT1-ZDT4都能找到Pareto前沿，在ZDT4上，QPSO只找到少量最优解，DCI-QPSO、NSGA-II和HQPSOGA的解分布不均匀，DCI-HQPSOGA的解在Pareto前沿均匀分布。

结合表1-表4中数据分析，GD指标中，QPSO在ZDT1-ZDT3值最小，说明QPSO的收敛性最好，但在ZDT4中效果较差，说明多目标条件下的QPSO易陷入局部最优，DCI-HQPSOGA在ZDT4表现最优，说明DCI-HQPSOGA在易陷入局部最优的环境下收敛性最好；IGD和HV指标中，NSGA-II在ZDT4优于QPSO，但不如HQPSOGA和DCI-HQPSOGA，DCI-HQPSOGA在ZDT4表现最优，且DCI-QPSO在ZDT4优于QPSO，说明本文多样性判别方法有效提高了算法多样性，不易陷入局部最优；Spacing指标中，NSGA-II优于HQPSOGA，说明NSGA-II中拥挤距离排序方法使种群在目标空间上分布更加均匀，DCI-QPSO表现最优，说明DCI-QPSO分布性较好，且DCI-HQPSOGA的分布性优于HQPSOGA，说明在本文多样性判别方法的影响下，DCI-HQPSOGA的分布性有所提高。

综上，DCI-HQPSOGA在种群多样性保持方面的各项指标上有明显优势，可较好克服粒子陷入局部最优的缺点，但在收敛过程中打乱了部分粒子飞行方向，影响了粒子的收敛速度。

4.2 DCI-HQPSOGA在WTA中的应用

各类型武器对目标的毁伤概率表和目标价值表如表5和表6所示[24]，其中Wi表示第i种武器。迭代次数MAX_Iter=3 000，武器种类数m=10，每种武器数对应为C=[3, 1, 1, 5, 1, 1, 1, 8, 1, 10]，目标数n=8。第iter次迭代的膨胀-收缩系数φ(iter)采用线性减小策略，phe∈[0.5,1]，phemax=1，phemin=0.5，φ(iter)计算如下：

φ(iter)=phemax-(phemax-phemin)×

iter/MAX_Iter

(12) 表5 武器对目标毁伤概率值表

表6 目标价值表

由于CLARANS嵌套在QPSO迭代过程中，为降低算法整体复杂度，δ分别取0.1、0.25、0.5、0.75和1，计算平均求解时间和算法收敛情况，所花时间如表7所示，收敛情况如图3所示。

表7 δ取不同值时所花时间表

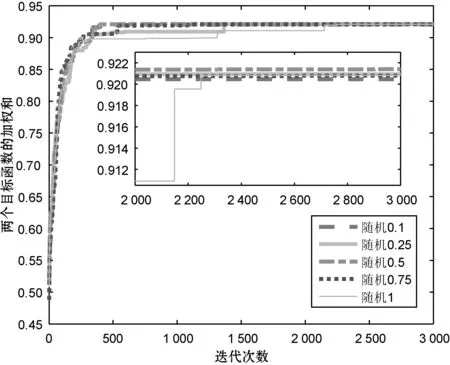
图3 非线性递减参数控制策略、不同CLARANS随机 次数下DCI-HQPSOGA的收敛效果

图3中，δ=0.5时结果最好，其次是δ=0.25、δ=0.75、δ=1，虽然δ=0.1效果较差，但与δ=0.5的差值小于0.002。考虑对求解效率的要求，δ=0.1是最好的选择策略，因此取δ=0.1，用DCI-HQPSOGA求解WTA问题。表8展示了非劣解对应的4种方案。

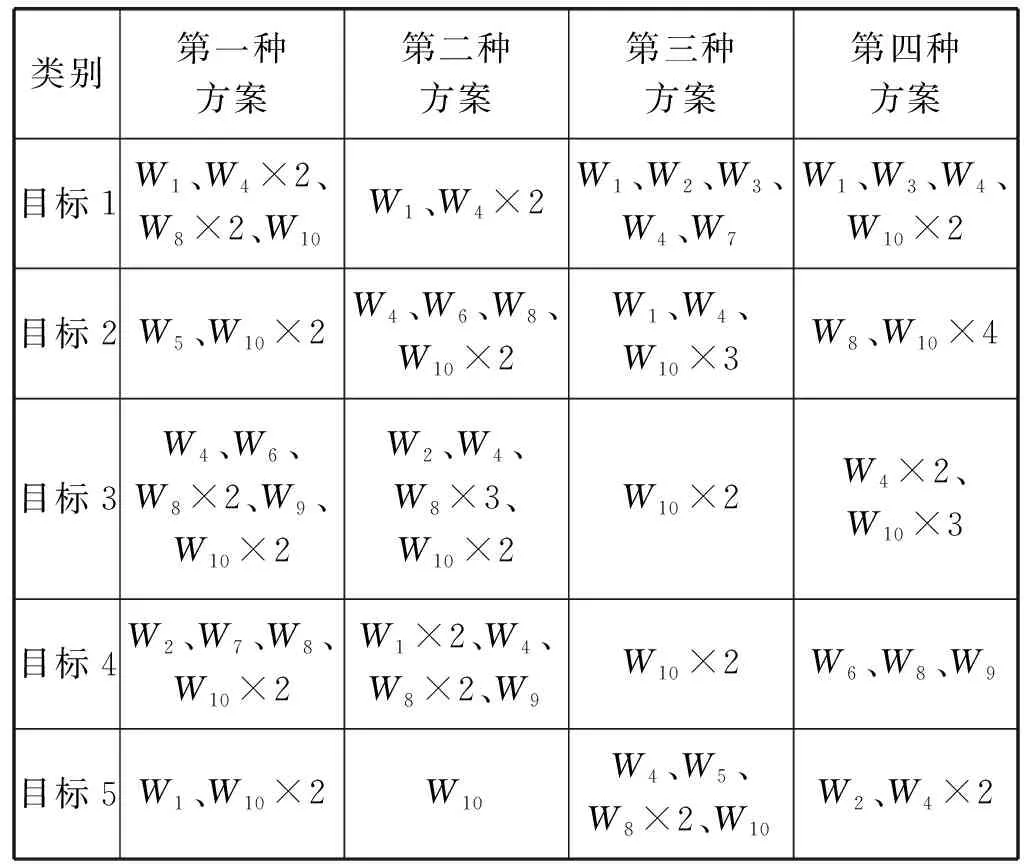
表8 DCI-HQPSOGA求解WTA问题的分配方案

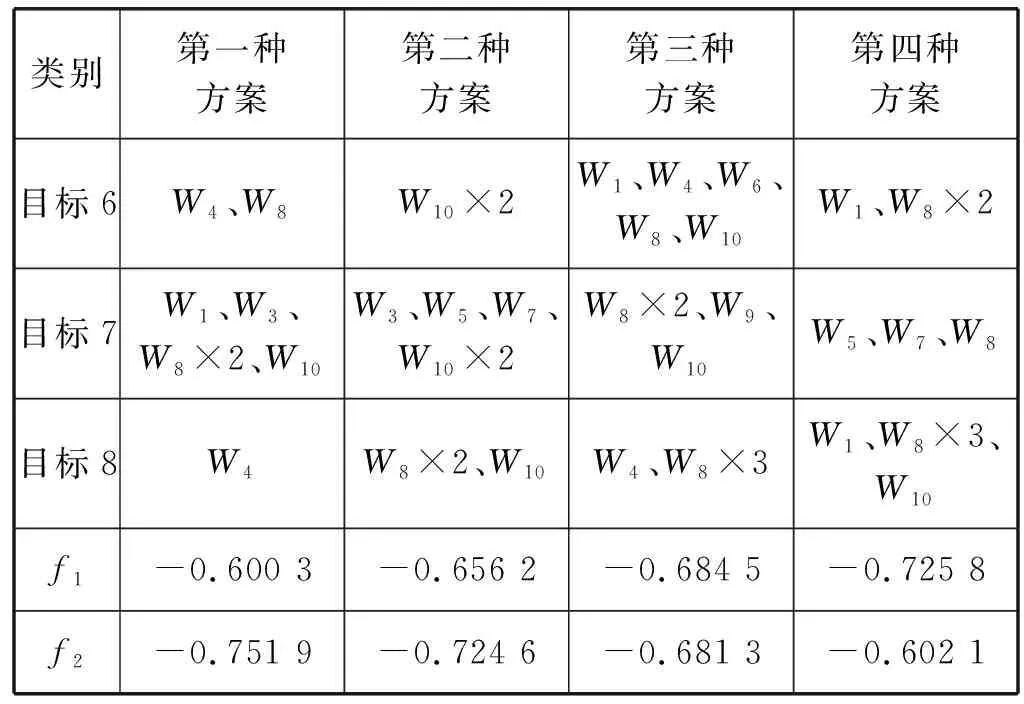
续表8

对比DCI-HQPSOGA与QPSO、DCI-QPSO、NSGA-II、HQPSOGA的Pareto分布曲线，观察各算法的收敛情况，结果如图4所示。

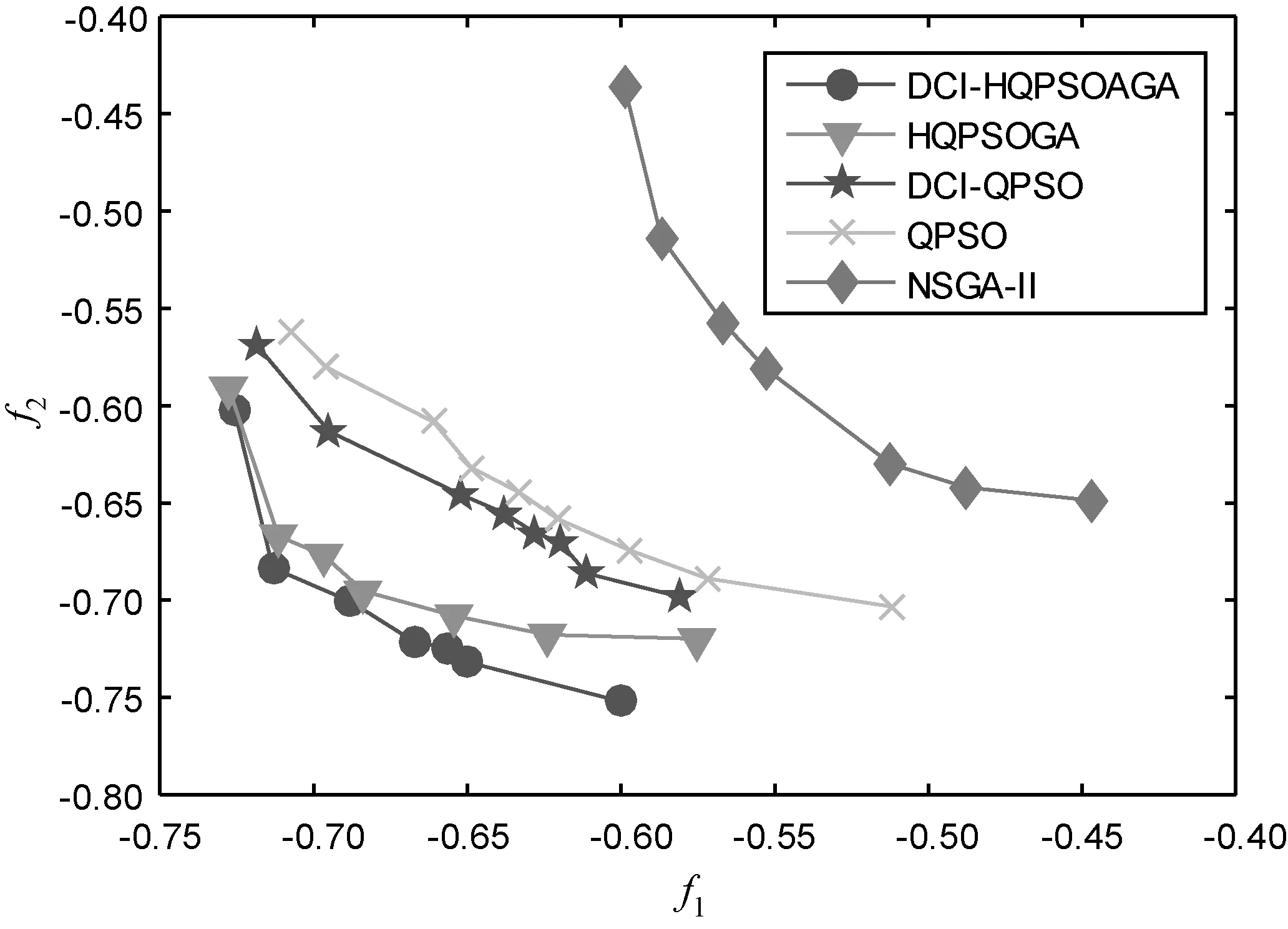
图4 δ=0.1情况下5种算法的目标函数收敛情况

可以看出，NSGA-II最差，可能的原因是分配矩阵较为稀疏，减弱了交叉和变异过程，使迭代寻优过程减慢；DCI-QPSO的解优于QPSO；DCI-HQPSOGA和HQPSOGA都可以取得较好的解，优于其他三种算法，且DCI-HQPSOGA的解最优，说明文中多样性判别方法的有效性。并且在DCI-HQPSOGA中引入文中多样性判别方法后，在WTA问题中具有较好的寻优能力，有效提高了求解精度。

5 结 语

本文先提出多样性贡献度的概念，利用CLARANS和模糊贴近度原则对HQPSOGA中QPSO的粒子进行多样性判别，形成了一套多样性维护机制。通过在ZDT1-ZDT4测试函数中对比分析，表明本文方法对算法多样性保持有一定改进。将改进算法DCI-HQPSOGA应用到SWTA问题，仿真结果表明该算法相比QPSO、DCI-QPSO、NSGA-II和HQPSOGA，能够提供更有效的WTA方案，为更精确的火力打击提供了更多可能。本文算法的不足是牺牲了一定的求解效率换取求解精度，所以如何在保证求解精度的同时，提高求解效率将是今后研究的方向。