基于小数量贴片天线的信号波达方向测试方法
2021-11-14侯天为龚文飞赵起超孙昕
侯天为 龚文飞 赵起超 孙昕
北京交通大学 电子信息工程学院,北京 100044
0 前言
信号波达方向(Direction of Arrival,DoA)估计是阵列信号处理领域的一个重要方向,其被广泛应用于军事领域及民用领域。DoA估计可以判断信号源的几何方向,并在无线通信中提高波束成形的效率和准确度。DoA估计也可以被用于干扰源定位、无线通信、无线传感网络和地震学中[1-3]。总之,一种准确且高效的来波信号方向估计系统在工程应用中具有重要作用。
目前,经典的来波信号方向估计方法主要有传统法、子空间类算法、最大似然算法以及综合类算法[4]。文献[5]提出了基于多重信号分类(Multiple Signal Classification,MUSIC)的子空 间 算 法。MUSIC算法在低信噪比小快拍数的情况下分辨率降低,在实际工程应用中实现难度较大;文献[6]提出了一种改进的MUSIC算法,可在低信噪比小快拍数的情况下改善分辨率,但需要进行大量的矩阵运算,计算复杂度较高;文献[7]提出了基于旋转不变信号参数估计技术(Estimating of Signal Parameter Via Rotational Invariance Techniques,ESPRIT)的DoA估计算法。ESPRIT算法需要偶数个天线阵子,天线阵子利用率低,而且不能估计相干信号的方向;文献[8]提出了一种基于Toeplitz矩阵集重构的相干信源二维DoA估计算法,可以解决相干信号的DoA估计问题,但是需要的阵子较多,阵子效率低;文献[9]提出了基于子空间拟合的最大似然算法,该算法提高了矩阵处理的维度,增加了计算量,降低了DoA估计的实时性;文献[10]提出的基于切比雪夫方法的综合法和文献[11]提出的基于凯瑟泰勒方向图综合法需要较多的天线阵子,不能降低民用领域DoA估计的成本,也不能将其应用于便携式终端中;文献[12]提出了一种三维空间比幅测向算法,该方法需要6个天线,而且当俯仰角较高时,估计误差增大。
由于地面通信普遍忽略用户和基站的高度差,故传统的利用平面天线进行DoA估计的算法只进行一维到达角估计,没有考虑二维到达角估计的问题。在第五代移动通信系统中,例如无人机通信系统中发射机和接收机的俯仰角较大,所以来波信号俯仰角的估计对信号源的确定具有重要意义。此外,传统的DoA估计系统需要较多的天线阵子,阵子利用率低,且多阵子DoA估计系统对终端的外形尺寸要求也更高。基于以上局限,我们研究了小数量天线的来波测向问题。
本文提出了基于小数量贴片天线的来波测向方法,利用比幅测向原理对DoA进行准确估计。该系统可在民用方面实现DoA估计的功能,适用于便携的用户终端,如手机和手表等。
综上所述,本文的贡献如下:
(1)针对基于子空间算法DoA估计复杂度高的问题,我们提出了基于比幅测向[10]进行DoA估计的方法,通过建立空间查找表,对每个区域的来波信号方向进行精确估计。针对传统的DoA估计算法阵子数较多,占用空间大的问题,我们提出了利用贴片天线阵列,利用其对空间不同来向信号增益不同的特点实现对来波信号二维DoA估计;
(2)基于传统信号方向估计算法阵子利用率低的问题,我们提出将空间分为3个区域,先对来波信号到达区域进行粗估计,再在每个区域中精确估计DoA。此方法提高了天线阵子效率,利用3个贴片天线可实现对半空间来波信号方向的准确估计;
(3)本文利用Matlab完成了对小数量贴片天线来波测向系统的仿真验证与结果分析。结果显示,该系统可以对空间任意方向来波估计,且随着仿真次数的增加,估计结果趋于稳定,估计误差在0.5°左右。
本文的章节安排如下:第一节主要阐述了信号方向估计的研究意义和传统信号方向估计算法的局限,并对本文研究成果进行了介绍;第二节主要分析了信号建模方法与天线阵列建模方法;第三节主要阐述了比幅测向算法的基本原理与改进的基于空间查找表的信号估计方法;第四节主要验证了小数量贴片天线系统对来波信号方向估计的准确性;第五节总结了本次研究结论。
1 阵列模型与信号模型
1.1 阵列模型
在DoA估计系统中,为了获得准确的估计结果,实际工程应用中通常采用平面螺旋天线。理想情况下,为了方便分析问题,通常用高斯函数近似平面螺旋天线的方向图。平面螺旋天线在水平面的方向图表达式为:

其中,θ——来波方向与天线波束轴的夹角;
G(θ) ——天线增益;
K——比例常数;
θB——天线方向图3 dB带宽。
理想情况下,平面螺旋天线二维方向图的直角坐标和极坐标表示如图1和图2所示。平面螺旋天线二维方向图对各个方向的增益进行了归一化,即方位角为90°时天线增益最大为1。
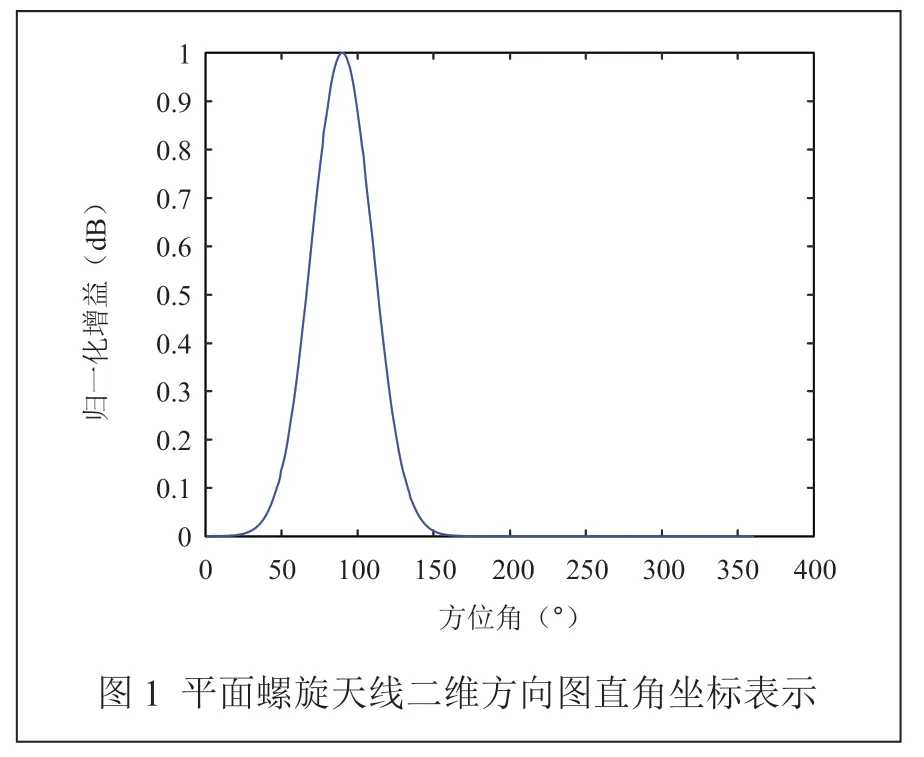

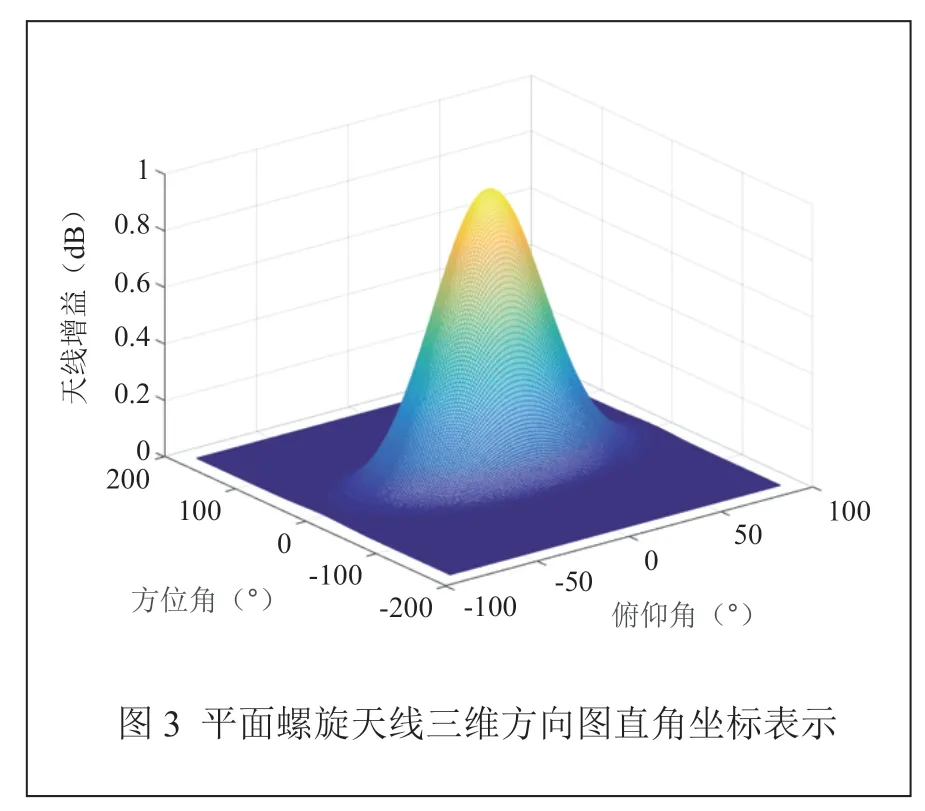
平面螺旋天线的三维空间极坐标方向图可由平面螺旋天线二维空间极坐标方向图绕轴线旋转一周得到。平面螺旋天线三维方向图直角坐标表示如图3所示。下文天线方向图与图3类似,将以此天线方向图为基础,对小数量贴片天线的来波测向系统展开研究分析。
传统的比幅测向算法只考虑了天线的二维方向图,只能对来波信号方位角估计,没有估计来波信号俯仰角的能力。由图3可知,方位角相同俯仰角不同时,天线增益不同,所以三信道贴片天线来波测向系统可以通过采用3个相邻的贴片天线实现对来波信号的二维到达角的准确估计。
三信道贴片天线来波测向系统天线阵列图如图4所示。天线阵列中共有3个贴片天线,每个天线对应一个通道,3个天线均匀分布在x-o-y平面。1号天线位于x轴上,逆时针方向依次为2号、3号天线,且天线之间夹角为120°。
由于3个贴片天线均匀分布在一个圆周上,故可将三阵子贴片天线来波测向阵型等价成均匀圆阵,以坐标原点为参考点,信号到达不同阵子时会产生一个时延τ。当来波的方位角为θ时,即来波在x-o-y平面投影与x轴正方向的夹角为θ,俯仰角为φ,即来波方向与z轴正方向的夹角为φ时,信号到达阵列天线中第m个阵子与到达参考点之间的传输时延τm0为:


其中,R——均匀圆阵半径,一般为半波长;
c——真空中光速。
小数量贴片天线增益受来波信号方位角和俯仰角的影响,所以天线阵列中第i个阵子对来波方向为(θ, φ)的信号的天线增益可表示为Si(θ, φ)。
由式(2)可得,贴片天线的来波测向阵列导向矢量a(f0)为:

1.2 信号模型
为建立完整的信号模型,模拟的窄带信号需满足以下要求:为使阵列流型矩阵满秩,令信号源个数不大于阵子个数,本文假设只有一个信号源;为使接收信号共面,令接收信号为远场平面波;为忽略天线阵列的边界效应与阵子互耦,假设接收阵子为理想天线阵子;为使阵子可近似为一点,假设接收天线阵列阵子间距远大于阵子的几何尺寸。
假设在自由空间中天线阵列阵子个数为M,干扰源个数为P,窄带信号为s(t),信号的复包络s(t)为:

其中,u(t) ——信号的幅度谱;
ω0——信号频率;
φ(t) ——信号的相位。
在空间中传播时延经过实验τ后,信号的复包络s(t-τ)为:
由于信号为窄带远场信号,短时间内信号包络基本不变,故可得:

将式(6)带入式(5),可得:

天线阵列中第k个阵子接收的数据xk(t)为:

其中,P——远场信号个数;
Ski——天线阵列中第k个阵子对第i个信号的天线增益;
τki——来波第i个信号到达第k个阵子与参考位置的传输时延;
nk(t) ——空间中噪声。
则天线接收数据的矩阵表示为:

则式(9)的矢量形式为:

其中,X(t) ——天线阵列接收的数据矩阵;
A——窄带远场信号的阵列流行矩阵;
S(t) ——信号矩阵;
N(t) ——天线阵列接收的噪声信号矩阵。
2 比幅测向算法原理
小数量贴片天线的来波测向系统采用相邻的3个贴片天线,通过比较贴片天线接收的来波信号功率来估计来波信号方向,从而实现对任意来向信号精确DoA估计功能。
小数量贴片天线的来波测向系统天线波束覆盖图如图5所示。以x轴正方向为参考方向,相邻的天线轴线之间的夹角为120°,1号天线的轴线方向与x轴重合,2号天线轴线方向与120°角方向重合,3号天线轴线方向与240°角方向重合。由图5可知,每个天线覆盖120°方位角的范围,将空间分成a、b、c3个区域。区域a的覆盖范围为空间角241°~60°,区域b的覆盖范围为空间角61°~180°,区域c的覆盖范围为空间角181°~240°。
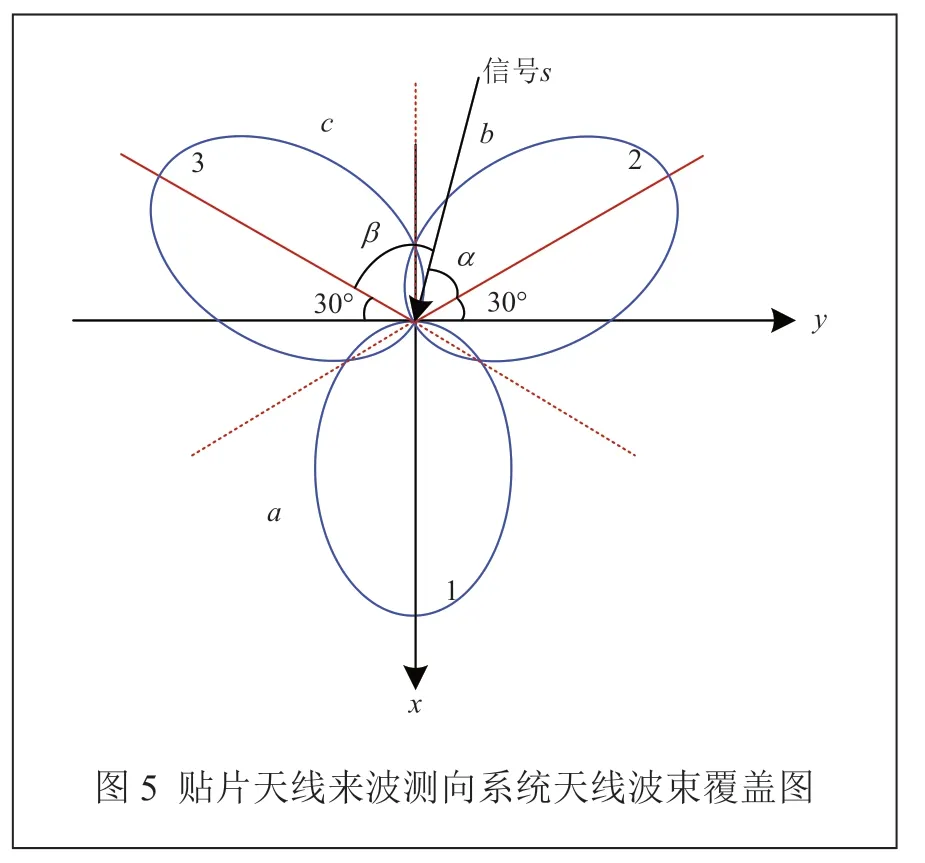
该系统将空间分成3个区域,通过比较3个天线接收信号的功率即可粗估计来波范围是区域a、区域b还是区域c。
假设天线i接收的信号功率为Gi,当3个天线接收的信号幅度关系为G2>G3,G2>G1,则可以判定来波大致方向为区域b,确定来波信号大致区域后需要精确估计来波方向,来波信号方向的精确估计需要进一步比较天线1、天线2和天线3接收信号的功率值。因此,比幅测向算法可以分成来波信号方向粗估计和来波信号方向精估计两步。
以平面贴片天线为例,当来波信号的角为θ,且来波方向与天线2和天线3轴线的夹角分别为α和β时,3个天线接收信号的功率可表示为:
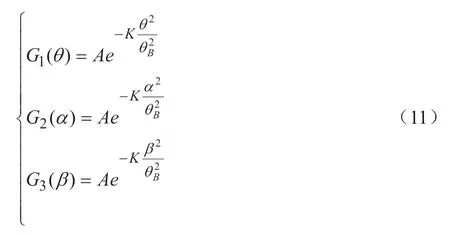
由式(11)可知,天线2接收的信号功率与天线1接收的信号功率比S21为:

天线2接收的信号功率与天线3接收的信号功率比S23为:

由图5可知,来波信号到达角θ与来波信号和天线2轴线的夹角α的关系可以表示为:

由式(12)、式(13)和式(14)可得方程组,解得信号到达角。
由于在工程应用中存在各种干扰,而且数据处理过程中计算误差较大,故估计结果的准确不高。因此,可以对传统的比幅测向算法的结果校正,进一步提高比幅测向精度。
常用的比幅测向校正方法是建立空间查找表。通常将贴片天线来波测向系统置于暗室中,记录不同来波方向下每个天线阵子接收信号的功率,计算贴片天线接收信号的功率比,从而在每个信号到达角下得到一组天线接收信号功率比值的对照表。在实际应用中,计算出实际天线接收信号的功率比,与标准查找表对照,找出差距最小的一组作为来波信号方向估计的结果。通常对于来波信号的二维到达角的估计也可用上述方法。假设来波信号来自区域b,当信号的到达方向为(θ, φ)时,来波信号DoA估计步骤如下:
(1)在暗室中记录每个来向下天线阵子接收信号的功率比值,得到3个区域的任意来波信号到达角的查找表;
(2)接收待测信号,获取3个天线接收信号的功率G1(θ, φ)、G2(θ, φ)、G3(θ, φ);
(3)寻找天线接收信号功率的最大值,粗估计来波信号到达的大致方向为区域b;
(4)计算查找表中不同天线接收数据的功率比s21(θ, φ)和s23(θ, φ);
(5)设估计误差S为:

在区域b的空间查找表中查找使估计误差S最小的一组方向作为精估计结果。
算法结构如表1所示。

表1 基于空间查找表的比幅测向算法
3 仿真实验与结果分析
为验证基于小数量贴片天线系统对来波信号DoA估计的准确性与有效性,本节对不同方向来波信号的DoA进行了仿真验证与结果分析。
假设仿真环境理想,天线阵列中的阵子无幅相差异,且各向同性,建立如图4所示的贴片天线来波测向系统天线阵列图。
首先,在实验之前建立分辨率为1°的空间查找表,为量化仿真误差,设均方根误差MSE(θ, φ)为:

(θi,φi) ——来波信号准确到达角。
假设信号数P为1,信号方向(65°,40°),干噪比SNR为20 dB,干扰频率f为4.44 GHz,快拍数K为1,000,仿真结果为(64.8°,39.6°)。在理想条件下,当信号源单一时,小数量贴片天线系统可以精确搜索到信号到达角度,可以以较高的分辨率估计信号二维到达角。
图6验证了小数量贴片天线系统对空间中任意来波角度估计的准确性。假设信号源数P为1,信噪比SNR为20 dB,其他参数不变,来波信号俯仰角从1°逐渐增加到90°,来波信号方位角从1°逐渐增加到360°,遍历全向空间各个来向角的估计均方误差,全向空间到达角估计结果如图6所示。
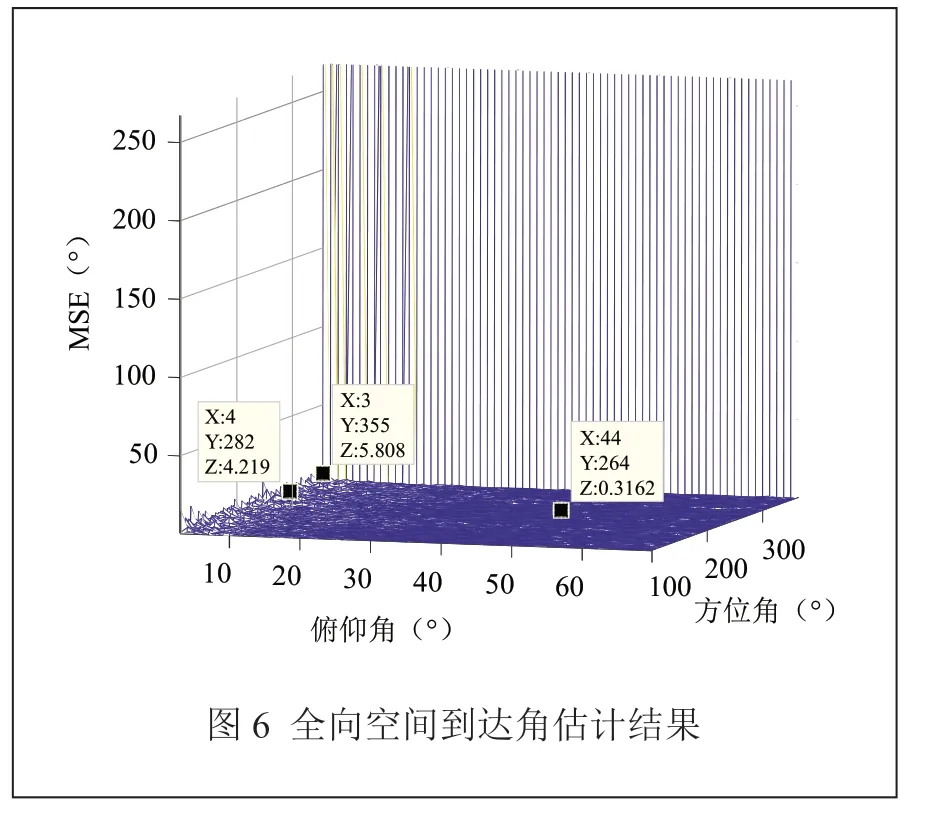
由图6可知,当方位角为360°时不能准确估计来波信号方向;当方位角低于360°,俯仰角低于5°时,估计误差较大,为5°左右,因为当俯仰角小于5°时,来波信号几乎垂直天线阵列,系统中每个天线接收的信号功率几乎相等,所以估计误差较大;当来波信号方位角低于360°,俯仰角大于5°时,不同阵子接收的信号功率差异较大,系统可以准确估计信号到达角,误差在0.3°左右。
图7和图8验证分析了方位角和俯仰角分别对系统估计准确度的影响。仿真分析系统估计误差随俯仰角变换曲线,计算在每个俯仰角下,各个方位角来波信号估计误差的均值。估计误差随俯仰角变换曲线如图7所示。仿真分析系统估计误差随方位角变换曲线,计算在每个方位角下,各个俯仰角来波信号估计误差的均值,估计误差随方位角变换曲线如图8所示。


由图7可知,当俯仰角小于5°时,估计错误,因为俯仰角小于5°时,信号方向垂直阵列,各阵子接收的信号功率几乎相等,所以估计错误;当俯仰角大于5°时,估计误差较小,约为1.5°,且随着俯仰角的增加估计精度逐渐趋于稳定,因为随着俯仰角的增加,不同阵子接收的信号功率差异逐渐增大,所以比幅测向算法可以利用阵子间功率的差异准确估计来波信号方向。
由图8可知,当方位角大于355°时,随着角度的增加,估计误差越来越大;当方位角小于355°时,估计比较准确,误差约为2°左右,因为方位角接近360°时与方位角为0°时各阵子接收信号功率相近,所以容易引起估计错误。
图9验证了小数量贴片天线系统对空间中任意来波角度估计的稳定性。假设信号数P为1,信号方向(65°,40°),信噪比SNR为20 dB,干扰频率f为 4.44 GHz,快拍数K为1,000,进行500次仿真,计算并分析系统随着估计次数的增加对来波信号方向估计准确性的影响,估计误差随估计次数的变化曲线如图9所示。

由图9可知,当估计次数小于50次时,估计误差较大,在0.56°左右,随着估计次数的增加,估计精度稳定在0.46°左右。因为估计次数较少时结果容易出现偶然性,所以估计误差波动较大。因此,为了获得准确的估计结果,可以对来波信号进行50次DoA估计,取结果的平均值。
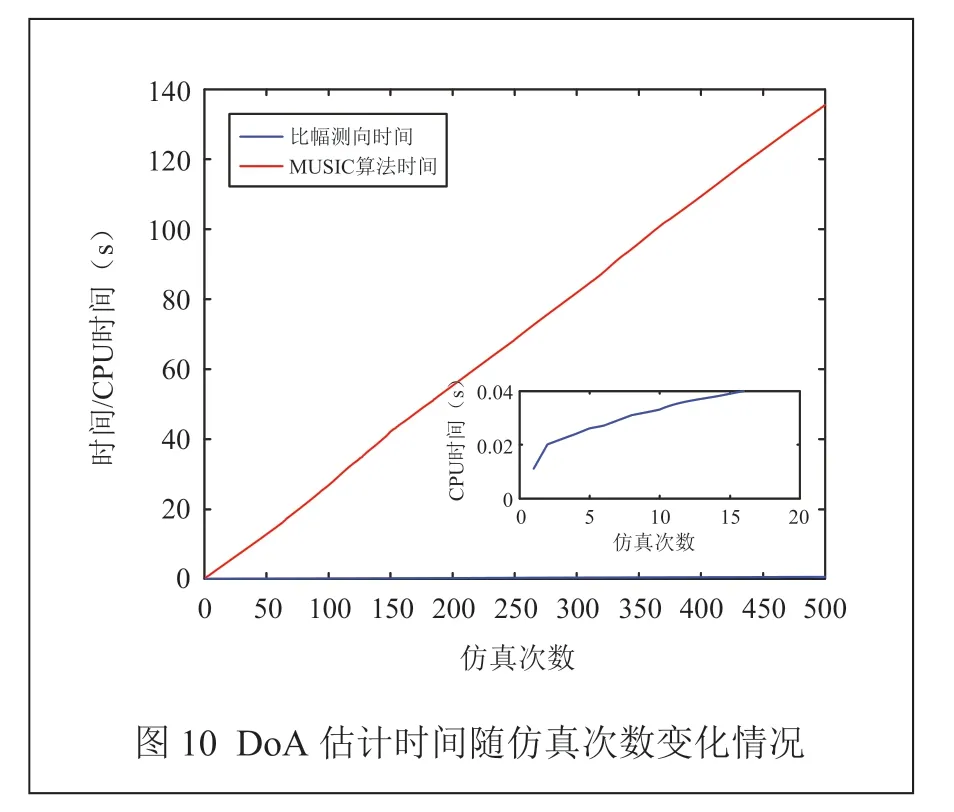
图10验证了该系统对DoA估计的时效性。假设信号数P为1,信号方向(65°,40°),干噪比SNR为20 dB,干扰频率f为4.44 GHz,快拍数K为1,000,进行500次仿真,计算并分析该系统与MUSIC算法统随着估计次数的增加对来波信号方向估计的时间累积结果,估计时间随仿真次数变化情况如图10所示,估计时间单位为CPU时间。
由图10可知,基于小数量贴片天线的来波测向系统和MUSIC算法随着估计次数的增加,时间也逐渐增加。从图10分析可得,MUSIC算法消耗的时间是比幅测向算法消耗时间的1,000倍,这是因为MUSIC算法需要进行如矩阵求逆等复杂的矩阵运算,所以MUSIC算法需要耗费更多的时间。
4 结论
在传统的比幅测向算法的基础上,本文进一步提高了阵子效率,利用3个全向贴片天线实现了来波信号DoA的准确估计,可以将该系统应用于较小的用户终端或者民众中。鉴于传统的比幅测向算法只能估计来波信号的一维到达角,本文提出的基于小数量贴片天线的来波测向系统可以实现对来波信号的二维到达角的准确估计。在此基础上,本文提出了利用空间查找表的方法查找信号到达角,极大地增加了方案的可行性,并且提高了方案的工程应用可行性。
