基于判别分类和回归计算的传感器节点定位
2021-11-14朱东进
朱东进,王 婷
(1.江苏电子信息职业学院 计算机与通信学院,江苏 淮安 223003;2.大连海洋大学 应用技术学院,辽宁 大连 116300)
0 引言
在传感器节点定位问题中,无线电或光信号强度的一个重要特性是信号衰减与距离的函数关系[1-4],这种关系构成了大量定位算法的基础。这些算法大致包含2个主要步骤:① 基于2个传感器之间发送/接收信号的信号强度来估计2个传感器之间的距离;② 通过三角测量或最小二乘误差方法,基于距离估计值来获得传感器节点位置[5-8]。近年来,已经提出了各种方法通过无线传感器网络跟踪区域中移动的一个或多个目标的算法[9-12]。
传感器网络可以看作是一种分布式模式识别系统。在模式识别方法中,不是将传感器位置和传感器读数转换为世界坐标系中的欧氏坐标,而是直接采用物理传感器给出的非欧氏读数。这些读数可以看作是对核函数的近似,而且所得到的函数空间可以看作是一个用于预测各种外部感兴趣量的协变量空间,可采用统计算法进行回归和分类。文献[13]提出了采用基于机器学习回归模型直接寻找移动用户在网络中的地理坐标。文献[14]提出了一种标签多伯努利目标跟踪与分类算法,把分类算法用于跟踪移动车辆。文献[15]在深入分析了RSS信号分布特性的基础上,提出了基于RSS信号变化率的子区域划分算法以及改进的AP近邻传播算法。文献[16]利用核方法进行统计分类和回归,从而为任意一对传感器位置提供一种广义的相似性度量。文献[17] 针对现有室内定位算法存在低精度,低实用性和低传感器利用率等问题,提出了一种基于多传感器融合的粒子滤波室内定位技术。
本文提出了一种完全绕开测距步骤的方法。首先将粗粒度定位问题作为一种判别分类问题,采用统计机器学习工具如支持向量机(Support Vector Machine,SVM)来求解,然后通过第二次应用粗粒度定位技术来实现细粒度定位。具体来说,定位算法包括2个阶段:首先,是一个训练阶段,选择一个合适的判别函数来使用任意构造的边界对位置进行分类。此阶段在少量位置已知的传感器(本文称为基本传感器)上在线或离线进行;其次,一旦训练阶段结束,其他位置未知的大量低功率传感器可以通过回归计算来局部确定自己的位置,从而实现传感器网络的节点定位。
1 核分类算法原理

对于核分类算法(如SVM),其核心是核函数K(x,x′)的概念,它给出了X中2个数据点x和x′之间的相似性度量。从技术上讲,要求K是一个对称的半正定核。对于平移不变核,即K(x,x′)=h(x-x′),对于某个函数h,如果h的傅里叶变换是非负的,则K是半正定核。对于这样的函数,Mercer定理指出,一定存在一个特征空间{Φ(x)|x∈X},在这个特征空间中,K为内积,即K(x,x′)=〈Φ(x),Φ(x′)〉。然后,SVM和基于核的相关算法在这个特征空间中选择一个线性函数f(x)=〈w,Φ(x)〉,使得对于某个常数B有‖w‖≤B,并使得训练误差最小,即:
(1)
式中,φ表示一个为凸的合适的损失函数,且对于0-1损失,指示函数II(y≠sign(f(x)))是一个上界。指示函数II(·)定义为如果A为真,则II(A)=1,否则为0。如SVM算法基于损失φ(yf(x))=(1-yf(x))+(下角标“+”表示x+=max(x,0))。f(x)也可以直接用核函数K表示:
(2)
存在大量核函数满足SVM算法所要求的半正定特性,如对于衰减参数σ和常数γ的高斯核:
K(x,x′)=exp[-(‖x-x′‖2/σ)],
(3)
以及多项式核:
K(x,x′)=(γ+‖x-x′‖)-σ。
(4)
这2个核函数随距离‖x-x′‖的增加而衰减,这是大多数基于信号强度模型共有的一个特性。特别地,无线电信号模型式(1)具有类似于多项式核的形式。文献[9]表明采用声能模型进行定位是合适的,该模型具有高斯核的形式。这就激发了直接采用信号强度来构造一个合适的半正定核函数,然后将它用于寻找一个判别函数,以达到定位的目的。由于仅对训练和测试数据点的K(x,x′)的值感兴趣,所以只需要确保Gram矩阵K=(K(xi,xj)ij)为半正定矩阵。
核方法的使用也使得合并多模态信号变得简单明了。实际上,假设有D种类型的感知信号,每种都可以用于定义一个核函数Kd(x,x′)(d=1,2,…,D),则Kd的任何二次组合都会得到一个新的半正定核:
(5)
根据经验,通常选择参数βd>0。
2 基于判别分类和回归的定位算法
2.1 算法描述
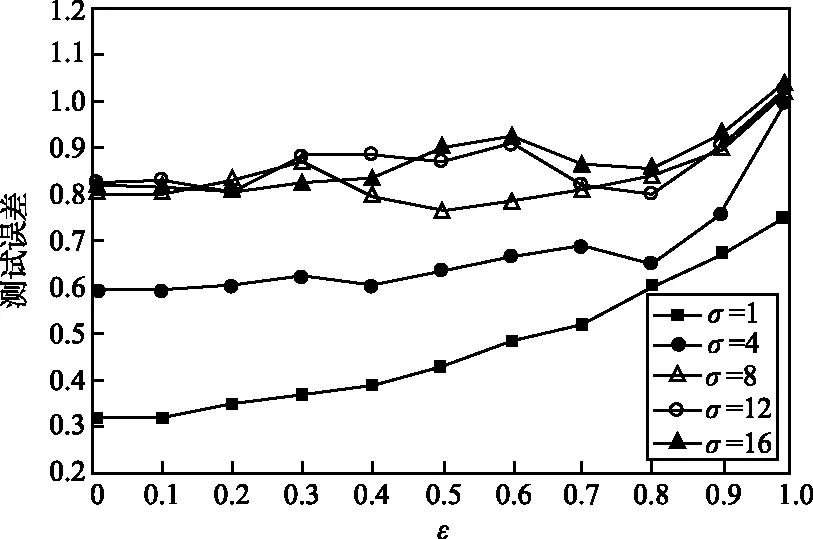
本文研究的定位问题是基于少量传感器(称为基本传感器)的已知位置来确定大量位置未知的传感器的位置,所以算法不需要关于网络拓扑的假设。假设有大量的传感器密集部署在一个地理区域。算法的输入是一组m个传感器,令X1,X2,…,Xm表示m个传感器的位置,即xi表示传感器Xi在R2(二维)中的位置。假设前n个传感器位置已知,即X1=x1,X2=x2,…,Xn=xn(n< (6) 注意,f(xj)的值是已知的,因为核K(xi,xj)的值是已知的,尽管现在还不知道xj本身的位置。 下面来确定核矩阵K=(K(xi,xj))1≤i,j≤m。对于传感器节点的定位问题,本文选择: (1) 简单地定义K(xi,xj)=s(xi,xj),将它称之为第一层核。这隐含地假设矩阵S=(s(xi,xj))1≤i,j≤m是一个Gram矩阵(即对称半正定)。这对于真实的信号矩阵是一个合理的近似; (2) 定义K=STS,称之为第二层线性核,K总是对称半正定的。也可以说K是欧氏特征空间{Φ(x)}的内积,数据点xi的特征空间定义为: Φ(xi)=(s(xi,x1),s(xi,x2),…,s(xi,xm))。 (7) (3) 可以在欧氏特征空间{Φ(x)}上计算任何半正定核(如高斯核)。这将得到一个对称半正定矩阵,称之为第二层高斯核。 上述分类构建的特点是,训练点对应于基本传感器,因此在数量上是有限的,由于可以自由选择区域C来学习,因此问题实际上变得容易求解。 其次,获得定位的细粒度估计。用前面获得的粗粒度解作为传感器Xj(j=n+1,…,m)的定位算法的子过程,具体实现为:在传感器网络中生成许多重叠区域Cβ(β=1,2,…,U),对于每个β,对类Cβ构建一个相应的分类问题,并预测是否Xj∈Cβ。因此,Xj必须位于包含它的区域的交叉部分,例如,可以将它的位置xj指定为这个交叉部分的中心。假定为区域Cβ选择合适的粒度和形状,如果大多数分类标签是正确的,那么就能够获得对xj的良好估计。 在与每个粗粒度定位子过程相联系的训练阶段,即关于固定区域Cβ的分类,基于前面描述的基本传感器位置构建训练数据集。在系统级,通过使全部基本传感器将信号矩阵记录s(xi,xj)及其已知位置发送给中心站来实现,它包含在中心站接收和存储n2+n个数和中心站调用定位算法。需要求解以下最优化问题: (8) 式中,f(x)=〈w,Φ(x)〉;φ(yf(x))=(1-yf(x))+;c是一个固定的参数。这是一个凸优化问题,其对偶形式如下[9]: (9) 一旦训练阶段完成,每个基本传感器需要存储n个参数(α1,α2,…,αn),以便对新的(位置未知的)传感器进行分类。如果采用第一层核,新的传感器Xj(j=n+1,…,m)接收来自ns个基传感器i∈{1,2,…,n}的信号s(xi,xj)以及非零值αi,导致在时间和存储上的成本为O(ns);如果采用第二层线性核或第二层高斯核,则新的传感器Xj从ns个基本传感器i∈{1,2,…,n}接收有n个元素的信号向量(s(xi,x1),…,s(xi,xn)),导致在时间和存储上的成本为O(nns)。然后,K(xi,xj)可以从接收到的信号s(xi,xj)中以O(1)、O(n)、O(n2)的时间分别计算出第一层核、第二层线性核和第二层高斯核,再通过一个简单的计算(式(6))确定传感器Xj是否位于区域C。显然,定位步骤在局部(以分布式方式)进行,只需线性(对于第一层和第二层线性核)或二次(对于第二层高斯核)时间和存储空间(以n表示)。由于定位是根据需要进行的,其时间和存储成本不依赖于网络中传感器的总数目m。 (10) 假设大小为L×L的传感器网络被半径为R的k2个圆盘均匀覆盖,则传感器网络中任意给定点被大约π(Rk/L)2个圆盘覆盖。每个圆盘用于确定区域分类问题的区域。为了获得全部剩余传感器Xj(j=n+1,…,m)的细粒度位置估计值,需要求解k2个区域分类问题。令eβ(β=1,2,…,k2)为训练误差,则: (11) 由于区域的大小和形状由算法来决定,例如,圆/椭圆形状特别适合于高斯或多项式核。定义ε为全部训练误差的上限: (12) 因此,定位误差的预期上界为: (13) (14) 如果基本传感器位置对于全部k2个圆盘在特征空间{Φ(x)}中是线性可分的,即ε=0,则定位误差为O(L1/3R2/3n-1/6)。 上述分析保证了随着传感器的更加密集分布,定位性能得到改善。此外,分析还揭示了R和k对定位误差的影响:定位误差随着R的减小而减小。由于随着R的减小,k的最优值增大,导致计算量增加,因为有k2个圆盘需要分类。因此,R的改变意味着算法的定位精度和计算复杂度之间的权衡。这在后面的仿真中也得到了证实。 3.1.1 仿真设置 考虑一个大小为10×10平方单位的网络,基本传感器均匀分布在类似网格的结构中,总共有n2个这样的传感器,沿每个维度的基本传感器数量为n。目标是识别一个由信号读数s(xi,x)(i=1,2,…,n)给出的传感器位置x是否位于待确定的区域C中。 首先定义信号模型,在该模型的基础上产生传感器接收到的信号值。假设位置x1的传感器从位于x2的传感器接收到一个遵循衰落信道模型的信号值: s(x1,x2)=exp[-(‖x1-x2‖2+N(0,ε))/σ], (15) 式中,N(0,ε)表示独立生成的具有标准偏差ε的正态随机变量,这个信号模型是高斯核的随机形式,而信号强度模型是多项式核的随机形式: s(x1,x2)=[‖x1-x2‖+N(0,ε)]-σ。 (16) 其次,确定待识别的区域C。C由全部位置x构成,满足(x-v)TH1(x-v)≤R且(x-v)TH2(x-v)≤R,其中v=[5 5]T,H1=[2 -1;-1 1],H2=[2 1;1 1],这些特定的选择意味着C是一个相当复杂的形状,半径R用来描述C的大小。对于每个仿真设置(n,R,σ,ε),学习一个判别函数f,采用基本传感器位置提供的训练数据来描述区域C。一旦学习到f,就在网络中均匀分布的传感器位置上对分类进行测试。 3.1.2n对定位性能的影响 图1所示为采用随机高斯核模型得到的与网络中部署的基本传感器数量相关的测试误差,横轴表示沿网络每个维度的传感器数目,纵轴表示测试误差,测试误差定义为在网格中均匀分布的位置中,错误识别点数与位于C(R)内的点数之比。仿真中固定噪声参数ε=0、影响核函数随距离的增加而衰减的衰减参数σ=1和σ=7,改变n。图1表明,随着传感器网络的密集分布,定位误差减小。如果需要识别一个特定的区域,只需在边界周围的区域放置基本传感器,因为这些区域是支持向量的可能位置。 (a) 衰减参数σ=1 (b) 衰减参数σ=7图1 采用随机高斯核模型的仿真结果Fig.1 Simulation results using random Gaussian kernel model 3.1.3σ和ε对定位性能的影响 衰减参数σ用来描述信号强度关于传感器距离的灵敏度。对于高斯核,小的σ值意味着对于远距离的传感器,信号衰减就快。信号噪声参数ε描述信号强度的噪声,它不是关于距离的确定性函数。图2所示为ε和σ对定位性能的影响。 图2 衰减参数σ和信号噪声参数ε对定位性能的影响Fig.2 Effects of attenuation parameter σ and signal-noise parameter ε on positioning performance 在这组仿真中,将每个维度上的基本传感器数目固定为10,C的半径R=2,同时改变ε和σ。可以看到,随着噪声参数ε的增大,定位性能会下降,而对于更敏感的信号即σ较小时,退化越严重。此外,在固定ε时,当σ变小时,定位性能会提高。 3.2.1 仿真设置 网络设置与前面相同,只是n2个基本传感器现在整个区域内随机均匀分布,这意味着每个基本传感器最初放置在L×L(L=10单位长)正方形的一个网格点上,然后受到高斯噪声N(0,L/2n)的扰动。剩余的其他位置未知传感器的位置将采用本文的算法来确定。同样假设信号强度遵循高斯核模型的随机形式,信号噪声参数ε=0.2。 将第2节的算法应用于细粒度定位。算法包括对覆盖整个网络的多个区域重复应用粗粒度定位。选择这些区域为半径为R的圆盘,并在整个网络中均匀分布。令k为沿每个维度的圆盘数量,因此总共有k2个圆盘需要识别。仿真研究R、k和基本传感器数目n对定位性能的影响。 3.2.2n对定位性能的影响 图3所示为得到的仿真结果。可以看到,随着网络中增加更多的基本传感器,定位误差均值减小,这与2.3的理论分析相吻合,说明算法特别适用于足够密集的传感器网络。 图3 基本传感器数目对细粒度定位误差均值的影响Fig.3 Effect of the number of basic sensors on the mean value of fine-grained positioning error 3.2.3R和k对定位性能的影响 图4所示为得到的R和k对定位性能的影响。定位误差均值是在随机生成的20个传感器网络上仿真求平均得到。实验中保持ε=0.2、σ=2和n=10不变,改变R和k。2.3节的分析表明,对于每个R值,存在一个最佳的k值随着R的减小而增大。由于有k2个分类问题需要求解,计算成本一般会随着R的减小而增加;另一方面,最佳定位误差均值随R的减小而减小,这在图4中得到了证实。通过R和k的特性,可以清楚地看到计算成本和定位精度之间存在的权衡。 图4 圆盘半径R和圆盘数量k2对细粒度定位误差均值的影响Fig.4 Effects of disk radius R and disk number k2 on the mean value of fine-grained positioning error 3.3.1 实验设置 实验中采用TE Connectivity 微型传感器模块构建一个真实的传感器网络来比较本文算法和文献[8]的基于测距的定位算法的定位性能。具体是根据网络中的一些基本传感器接收到的光信号强度来估计光源的位置。硬件平台由25个基本传感器构成,放置在5×5的网格上,彼此相距10 cm。每个传感器模块由一个运行于3.5 MHz的Intel 8位处理器(具有128 Kb 的闪存和4 Kb 的RAM)、RFM TR1000 无线电、EEprom和一个传感器板(包括光、温度、麦克风传感器和一个探测器)构成。放置在基本传感器上的光源位置给出训练数据,把需要估计的81个光源位置均匀分布在9×9的网格中,网格分布在整个网络上。 3.3.2 实验结果 文献[8]的算法包括2个主要步骤:① 测距过程,建立基本传感器接收到的信号强度与到光源的距离之间的映射;② 定位过程,采用最小二乘法得到距离估计值。本文算法采用3种核,第一种是采用信号矩阵的第一层对称半正定近似,第二种和第三种是从信号矩阵构造的特征向量上定义的第二层线性核和高斯核。对于细粒度定位,将粗粒度定位重复应用于半径R=20 cm的圆盘,覆盖部分网络区域。这些圆盘中心在2个维度上相距5 cm,沿每个维度有10个圆盘(即k=10)。 表1所示为对于全部81个未知位置,本文算法采用3种不同核所得到的定位误差和文献[8]的基于测距算法得到的定位误差比较。可以看到,本文算法的定位误差明显低于文献[8]的算法的定位误差;在3种可供选择的信号核中,从信号矩阵构造的特征向量上定义的第二层线性核和高斯核要比简单的第一层核的定位效果要好。 表1 定位误差比较Tab.1 Comparison of positioning errors 本文针对自组织无线传感器网络提出了一种基于判别分类和回归计算的定位算法。算法避免了复杂的测距计算和传感器网络建模,测距计算需要精确的信号模型且很难校准。相反,本文算法采用信号强度或者直接为基于核的分类算法定义基函数,或者通过在信号强度测量值之上生成派生核间接地定义基函数;算法特别适合密集分布的传感器网络,在基本传感器上执行预处理,而定位步骤可以以线性时间在每个位置未知的传感器上进行。
2.2 算法实现细节和计算成本分析
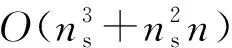
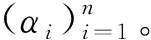
2.3 算法定位误差分析
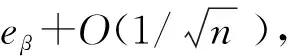
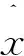
3 算法实验结果
3.1 粗粒度定位
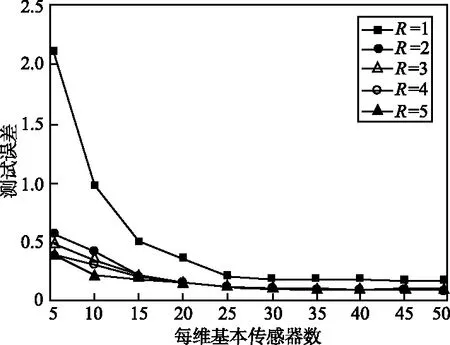

3.2 细粒度定位
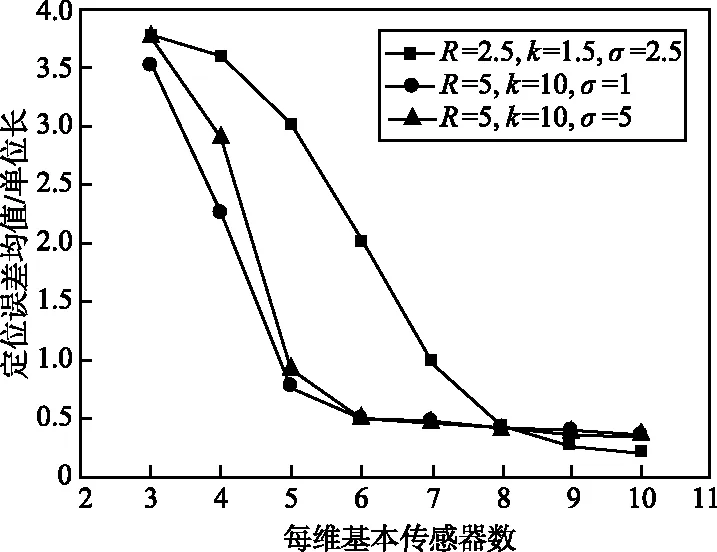

3.3 与采用基于测距的定位算法的比较
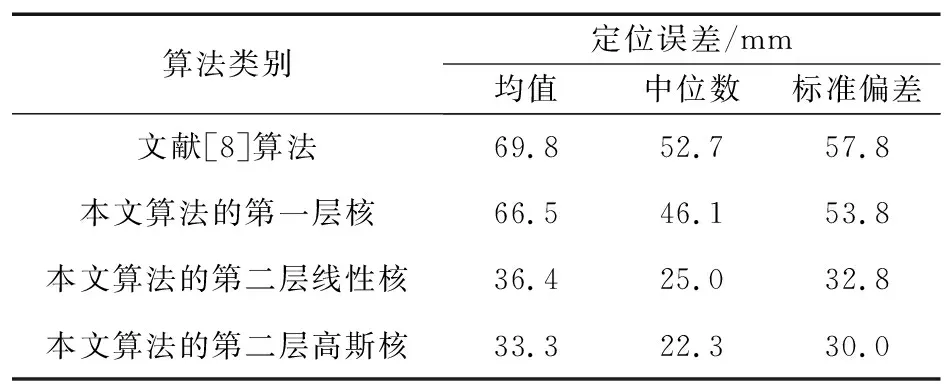
4 结束语
