基于LSTM模型的降雨短临预报

王式太,张定红,殷 敏* ,张博宇,程 波

(1.桂林理工大学 测绘地理信息学院，广西 桂林 541006；2.广西空间信息与测绘重点实验室，广西 桂林 541006；3.山东省地质测绘院，山东 济南 250002)

0 引言

降雨作为最常见的气象活动之一,对人们的生产生活产生着重要影响。虽然降雨现象在不同的气候、区域和季节会表现出一定的差异性[1]，但目前一般认为降雨是在温度、气压、相对湿度和大气可降水量(Precipitable Water Vapor,PWV)等多种要素的综合影响下发生，且PWV在很大程度上决定降雨强度[2]。相比探空站、微波辐射计等传统PWV测量手段，全球导航定位系统(Global Navigation Satellite System,GNSS)反演PWV由于能得到低成本的连续观测值[3-4],在降雨短临预报中得到了广泛的应用。文献[5]通过最小二乘方法拟合GNSS-PWV时序，通过分析PWV变化阈值达到预报强降雨的目的，并指出仅使用PWV阈值作为预报降雨的方式会导致误报率偏大；文献[6]通过对浙江地区连续运行参考站数据的分析，在不同月份设定不同PWV阈值作为判断降雨的条件建立模型，达到80%降雨准确预报率；神经网络模型由于能够拟合复杂过程被广泛应用于降雨预报[7-9];文献[10]通过基于PWV的多种数据，逐个月份构建多隐层的反向反馈神经网络预报降雨模型，能够预报出95%以上的降雨，并且误报率与传统方法相当。

然而在降雨发生的过程中,PWV数值会产生规律性变化，基于单个时段内PWV数值的降雨预报可能会忽视PWV连续变化的时间特性对于实际降雨现象的影响。因此，本文提出使用LSTM神经网络拟合PWV时序数据，在顾及时序变化的基础上，试图分析多种气象要素对构建模型的影响，来提高模型的预报能力；并在不同的时间尺度下分别构建预报模型，以评估模型对不同时间尺度降雨信息的敏感性，得到一个基于局部地区的最优预报模型。

1 PWV计算

由地基GNSS接收文件可解算得到对流层天顶总延迟(Zenith Total Delay,ZTD)，并使用Saastamoinen模型计算天顶干延迟(Zenith Hydrostatic Delay,ZHD)，结合式(1)、式(2)即可求得天顶湿延迟(Zenith Wet Delay,ZWD)和测站上空的PWV[11]：

ZWD=ZTD-ZHD,

(1)

(2)

为计算PWV,还需要得到测站实时的大气加权平均温度(Tm)，Tm真实值是由测站上空水汽压和绝对温度沿天顶方向积分计算，整理可以得到如下形式：

(3)

式中，T为地表温度；e为水气压；dH中的H为位势高度；Δhi表示第i层大气的高度差，n表示层数；Ti和ei分别表示第i层大气的平均温度和水汽压数值[12-14]。

水汽压为：

(4)

式中，es为饱和水汽压;Td为大气温度;RH为大气湿度。

使用探空站计算的Tm时间间隔为12 h，因此需要拟合Tm模型，用于解算逐小时观测的GNSS数据[15-16]。

由于在实际的气象活动中降雨发生的时刻远少于不发生降雨的时刻，因此选取降雨较为频繁的海南省海口市作为研究区域，减弱神经网络训练中过拟合现象。2015—2017年海口探空站的Ts和Tm的如图1所示。

图1 海口站Ts和Tm散点Fig.1 Scatter plot of Ts and Tm at Haikou station

从图1中的散点分布可知,Ts和Tm存在明显正相关的线性关系，利用最小二乘法拟合Ts和Tm，得到的Tm模型:

Tm=109.24+0.60×Ts。

(5)

将Tm模型应用于海口陆态网站点，结合式(1)和式(2)即可获取1 h分辨率的高精度PWV序列。

2 降雨现象的特性分析

使用2015—2017年海口陆态网站点的观测数据，分4个季节验证单个PWV数值对于降雨的影响。将同一季节所有降雨发生时刻前一小时PWV的均值作为阈值条件判断是否降雨，当PWV数值大于阈值时判定为发生降雨，使用阈值重新判断未发生降雨的历元，当未发生降雨历元的PWV大于阈值时，即认定为误报降雨，以误报降雨的历元和实际不降雨的历元的比值作为评价标准，当其数值越小则表明PWV数值对降雨的影响越大。结果如表1所示。

表1 PWV预报降雨方法的错误预警率Tab.1 Error warning rate of PWV rainfall forecasting method

由表1可以看出，在不同季节，PWV数值存在较大差异，如在2—4月中降雨PWV均值为36.29 mm，在8—10月中降雨PWV均值为60.34 mm，因此，在分析PWV对于降雨的影响时需要分季节验证。使用PWV阈值方法总体的错误预警率为28.3%，此种统计方法还未算入实际发生降雨，但PWV小于阈值被错误判断为不降雨的现象，因此仅仅使用单个PWV数值作为判断是否降雨的依据缺乏可靠性。

通过构建4个不同季节降雨过程中PWV和降雨量的时序对比，初步分析PWV变化特征与实际降雨发生时间的关系，PWV和实际降雨的时序对比如图2所示。

由图2可知，在降雨发生前一定时间内PWV会迅速增加，表现出峰值，在峰值出现后的一定时间内发生降雨，当降雨实际发生时PWV会由于冷凝现象减少，而且PWV的降低会随着降雨持续时间和降雨强度的增加表现出更大的幅度，如年积日为11的降雨现象中，由于降雨的持续时间近36 h，导致PWV数值在此时间段内表现出持续的降低。整体而言，PWV在降雨发生时伴随着降低的趋势，且PWV数值的减小先于降雨发生，因此利用PWV与降雨的负相关关系来预报降雨具备可行性。

(a) 年积日

(b) 年积日

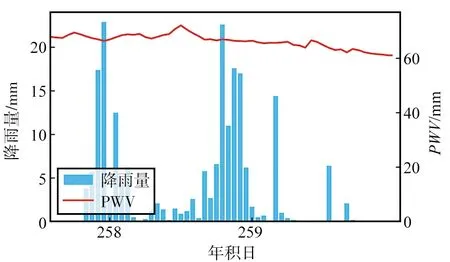
(c) 年积日

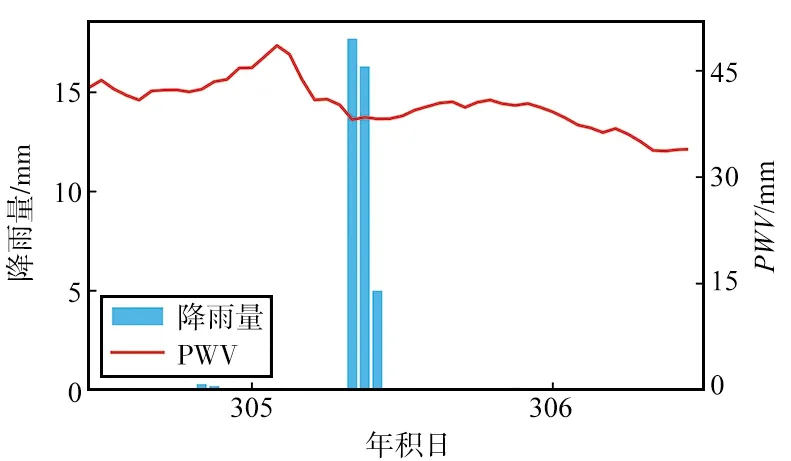
(d) 年积日图2 2015年PWV和逐小时降雨量的时序对比Fig.2 Time series comparison of PWV and hourly rainfall in 2015

为了验证PWV出现峰值与发生降雨的确切关系，通过延长对比时间构建PWV逐小时的变化量与实际降雨量的时序对比，如图3所示。

(a) 年积日

(b) 年积日

(c) 年积日

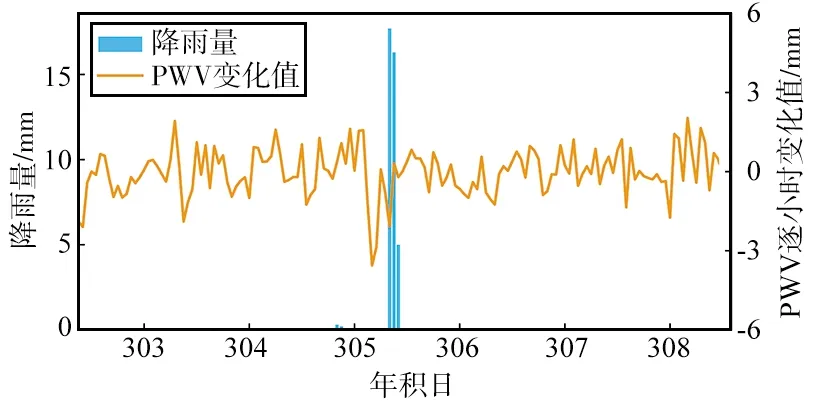
(d) 年积日图3 2015年PWV逐小时变化值和逐小时降雨量的时序对比Fig.3 Time series comparison of hourly variation of PWV and hourly rainfall in 2015

当降雨发生前一定时间内PWV变化值存在一个迅速增加，继而迅速减小的过程，但是当实际无降雨发生时PWV也会因为大气活动(如大气环流)而出现类似的波状起伏。虽然无降雨发生时PWV波动相比于强降雨时的PWV波动幅度较小，但仍会对普通降雨产生干扰。这一结论表明,降雨现象作为一个复杂的大气演变结果，PWV单一数值难以准确预报降雨，因此在LSTM降雨短临预报模型的构建中还应加入地面温度、地面气压、大气湿度、PWV变化值等其他参数输入，以达到提高预报降雨准确率的目的。

3 降雨预报

3.1 LSTM模型介绍

LSTM是一种计算时间序列的神经网络，通过对存在时序特征的数据样本训练，能够达到对数据拟合和预测的目的[17]。LSTM神经网络的输入数据为一个指定长度的时序信息，相邻时间步的隐含层分别计算权重，具备前后时间相连的特点；在模型回归过程中通过忘记门机制抑制梯度消失，从而更好地收敛；LSTM还具备记忆性，能够匹配时序数据长期特征的同时顾及短周期的变化特征，这一拟合机理与实际降雨现象的季节性周期变化具有类似的特点。

3.2 数据处理

实验中地面温度、地面气压、大气湿度3种数据从气象站获取，由于海口气象站和海口陆态网站点高度不同，使用气温垂直插值公式和气压垂直插值公式[18]将温度和气压归算至陆态网站点同一高度，PWV变化值通过2个相邻的时刻数值相减得出，逐小时降雨量采用气象站观测数据。

对数据的预处理包括剔除存在数据缺失的序列，并且由于LSTM模型需要输入连续12个时刻的观测值，所以对于存在空缺值的时序数据都需要剔除，避免错误数据对模型产生干扰。

以海口陆态网站点2015—2016年的观测数据作为训练样本，通过输入连续12个时序的地面气压、地面温度、大气湿度、PWV和PWV变化值5种参数训练模型，用2017年的数据作为测试集，检验LSTM神经网络模型短临预报降雨的能力，最终的数据样本数量如表2所示。

表2 数据样本量Tab.2 Data sample size

3.3 模型训练

用准确率(True Detection,TD)和误报率(False Alarm,FA)两个参数来评估LSTM模型预报降雨的可靠性、稳定性，其计算方法如式(6)和式(7)所示。其中错误预报降雨次数指实际没有发生降雨，但模型预报该时段发生降雨的次数；错误预报不降雨次数指实际发生降雨，但模型预报该时段不发生降雨的次数，即：

(6)

(7)

通过控制变量的方法依次剔除地面温度、地面气压、大气湿度和PWV变化值训练短临降雨预报模型，以全部5种数据输入的样本训练作为对比，比较分别缺失4种数据对于LSTM模型构建短临降雨预报的影响，训练中均已1～2 h尺度内是否降雨作为预测结果，预报降雨的能力如图4所示。

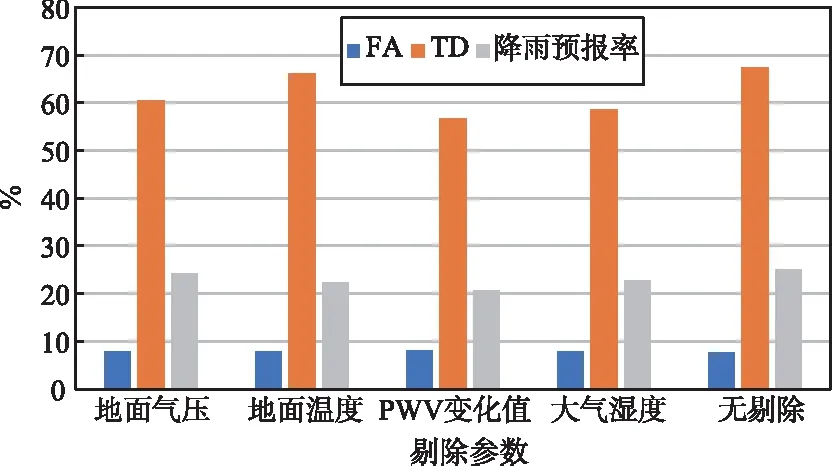
图4 不同气象数据对降雨预报的影响Fig.4 Influence of different meteorological data on rainfall forecast

由图4可知，气压、地面温度、PWV变化值和大气湿度均能一定程度上提升LSTM模型短临预报降雨的能力。其中地面温度对于模型的改善较弱，在准确率和误报率基本相同的情况下仅能略微提升降雨预报率；PWV变化值和大气湿度均能明显增加准确率；气压的加入能全面提升预报能力。因此将地面温度、地面气压、大气湿度、PWV变化值和PWV五种数据作为训练样本的输入参数能提高模型的可靠性。

为了探究海口地区LSTM网络模型对于预报降雨的最佳预警时间，在以相同的输入数据的前提下，分别以输入时序的1～2 h内是否降雨、1～3 h内是否降雨、1～4 h内是否降雨、1～5 h内是否降雨、1～6 h内是否降雨一共5种时间尺度的预报作为训练结果，比较不同时间尺度预报对应的准确率、误报率以及准确预报降雨次数，从而得出最佳的预报时间。训练模型的准确率、误报率、准确预报降雨次数和降雨预报率如表3所示。

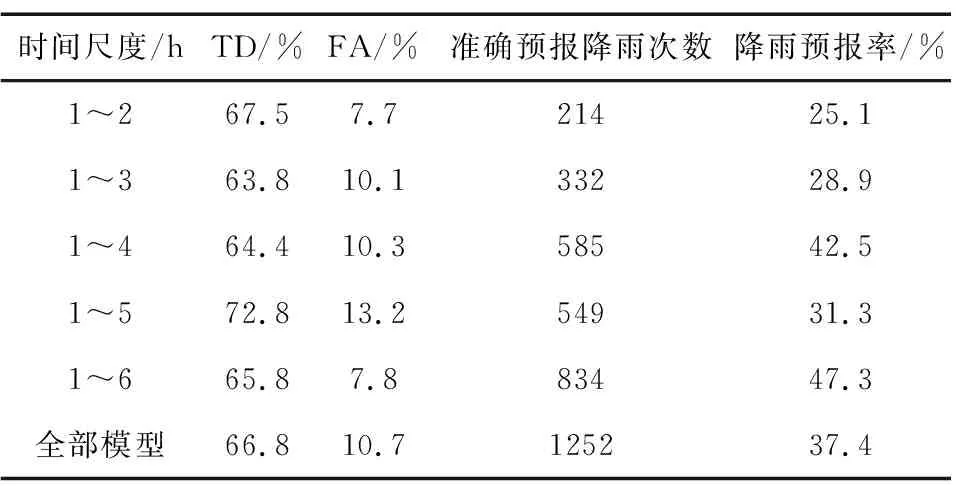
表3 不同时间尺度预报对应的TD和FATab.3 TD and FA corresponding to different forecast time scales

从表3中可知,使用LSTM预报降雨，其平均准确率为66.8%，略优于传统方法63%的准确率；平均误报率为10.7%，相较于传统方法36%有较大改善，但总体准确预报目标区域降雨的比例偏低，约37.4%，分析其原因可能为热带气候的水汽变化迅速，具备一定混沌性，LSTM模型在训练过程中存在部分过拟合现象。从表中可知针对海口地区的LSTM神经网络短临预报降雨模型，当预报时间设为1～6 h的情况下，其总体预报能力最优，准确率65.8%与传统方法相当，误报率为7.8%，能够准确预报47.3%的降雨；设置预报时间为1～5 h的情况下，预报能力次优，准确率和误报率都有所改善，能够预报31.3%的降雨；当设置预报时间为1～2 h的情况下，准确率达到最大值67.5%，同时维持较低的误报率，但只能预报25.1%的降雨；1～4 h预报时间到得的模型各项指数都比较均衡；1～3 h预报时间的模型整体性能最差。

通过对比不同时间尺度对应的准确率和误报率可知,1～6 h预报时间训练得出的模型整体预报降雨性能最优，1～5 h的预报模型性能较优。

4 结束语

本文构建了基于多气象参数的连续12个时序数据输入的LSTM神经网络降雨短临预报模型，结论如下：

① 通过分析不同季节降雨发生过程中PWV的变化特性,均发现PWV在目标区域具有较为明显的引导降雨作用，在降雨发生前约1～6 h PWV呈现规律性升高，表现出峰值，其中峰值突出越明显则预示着实际降雨量越大，使用PWV作为预报降雨的参数具备可行性。并且相比使用单个时刻的PWV数值预测降雨，一个连续时序的PWV数据预测降雨具有更优的可靠性。

② 地面温度、地面气压、大气湿度和PWV变化值均能增加模型可靠性，使用连续12个时间序列的地面温度、地面气压、大气湿度、PWV和PWV变化值作为LSTM模型输入参数，以预测时段内是否发生降雨作为训练结果，得到的所有模型的平均准确率和平均误报率2个参数分别优于传统阈值方法约5%和25%。通过设置不同的预警时间进行训练，最终得出针对目标区域1～6 h的预警的整体预报能力最优，1～5 h预报能力次优，整体误报率下降显著。