The interference between a giant atom and an internal resonator
2021-11-13XiaoPeiYangZhiKunHanWenZhengDongLanandYangYu
Xiao-Pei Yang,Zhi-Kun Han,Wen Zheng,Dong Lan and Yang Yu
National Laboratory of Solid State Microstructures,School of Physics,Nanjing University,Nanjing 210093,China
Abstract The Jaynes–Cummings model plays an important role in quantum entanglement and state measurements.Here,we discuss how to realize it in a waveguide-mediated interaction system,which comprises a giant atom and a resonator.We show the vacuum Rabi splitting and discuss how to achieve a unidirectional transport.We extend the Purcell effect in cQED to this waveguide QED system,showing how to control the giant atom decay rate.Our design can further be built experimentally and has application in quantum manipulation.
Keywords: interference,quantum optics,waveguide QED
1.lntroduction
Quantum computing based on circuit quantum electrodynamics(cQED)has made progress in recent years.We can use a resonator to realize quantum nondemolition measurement or control the qubit decay by the Purcell effect [1–4].However,due to the lithographic scalability,the number of superconducting qubits increases and could reach the noisy intermediate-scale quantum computing [5],limitation like chip size makes it hard to expand a quantum network.Beyond the cQED,one promising candidate scaling up the circuit is waveguide QED,which helps exchange information between distant components.
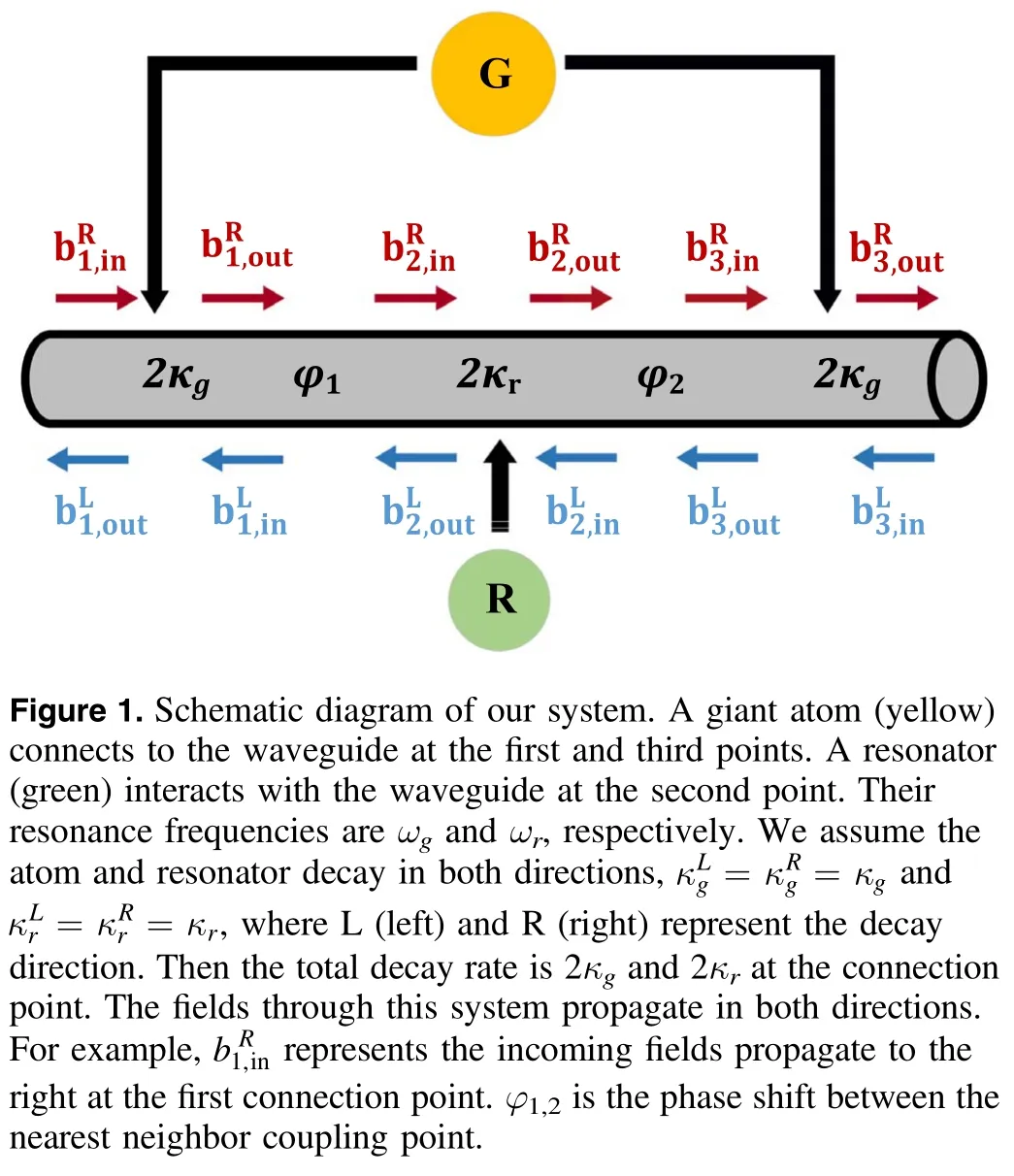
We can observe some optical phenomena like electromagnetically induced transparency(EIT)and Fano resonance in the waveguide-mediated interaction system [6–10].These interference effects depend on the frequency detuning and positions of qubits,holding the promise for application in quantum storage and quantum information.We can further put the qubits in specific separation,realizing atom-like mirrors or spatially entangled itinerant photons [11,12].However,the decay losses from the open environment limit the waveguide-mediated gate fidelity.As a potential solution,some theories and experiments based on “giant atom” attract attention [13–21].Here,the qubit has several connection points to the waveguide and is protected from decoherence by the interference effect.This design can also be extended to a large-scale quantum network.Beyond cQED and waveguide QED,some experiments based on the hybrid system show a nontrivial effect.For example,the interference between direct and indirect coupling paths helps to realize unidirectional transport [22,23].
Inspired by the discussion above,we explore a platform to realize these interference effects in a pure waveguidemediated interaction system.It helps understand the differences between these coupling regimes.In this Letter,we first introduce our model,where a resonator and an internal giant atom are coupled to the waveguide.Then we provide a theoretical analysis by using the single-photon scattering and input–output formalism.We show the interference effect,finding the Rabi splitting,complete transmissions,and EIT.We discuss their relationship with other coupling systems.In the end,we provide how to control the effective decay rate of the giant atom and compare the results with the direct coupling system.Our analytic results can be built experimentally and have applications in quantum manipulation.
2.Model and Hamiltonian
The system comprises a giant atom and a resonator,as shown in figure 1.The giant atom has two connection points to the waveguide,while the resonator has one.The Hamiltonian of the system is H=Hg+Hr+Hw+Hint,where Hg,Hr,Hw,and Hintrepresent the Hamiltonian of the giant atom,the resonator,the bosonic field in the waveguide,and the interaction terms,respectively [24,25].Under the rotating-wave approximation,it can be expressed as
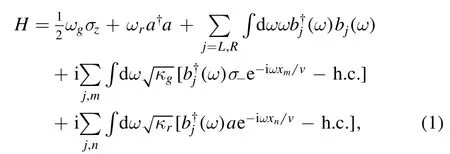

3.Single-photon scattering model
To obtain the information on this system,we consider the single-photon transport regime.According to the theory[26],S-matrix describes the relationship between the incoming and outgoing states,which satisfies

where∣ω〉describes the input state with frequency ω,∣ν〉describes the output state with frequency ν.We assume these free states exist long before t0→-∞and long after t1→∞their interaction with the giant atom and the resonator.Then the operator S can be expressed as

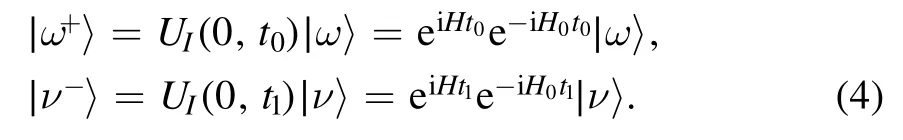
We assume the system is initialized in the ground states ∣0〉 .For the field towards right,the outgoing operator satisfies
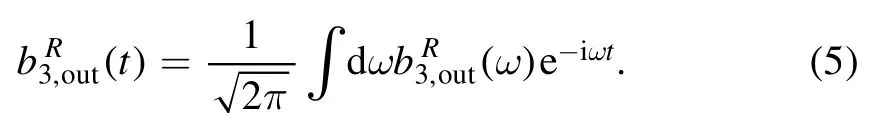
Using the equation above,we can rewrite the single-photon scattering matrix as
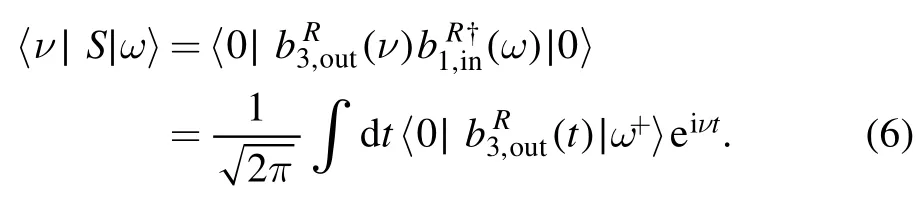
The transmission spectra is determined byIn the following,we will discuss how to get it by the input–output formalism.
4.lnput-output formalism
Now,we consider the device works in the weak coupling limit and the Markovian regime,where we can neglect the field propagation time between the connection points.The equation of motion for the giant atom is
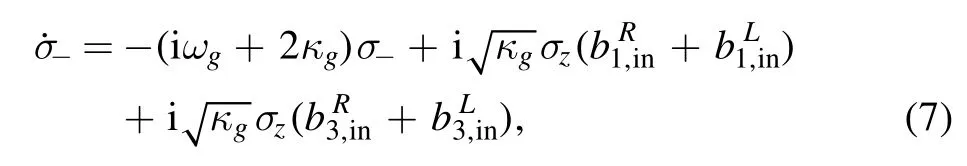
whererepresents the right-propagation field at the first connection point.The equation of motion for resonator is
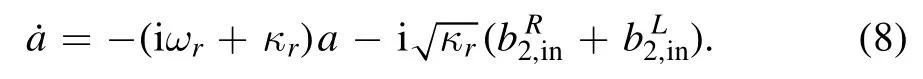
According to the input and output theory [26,27],we can further obtain the field toward right as
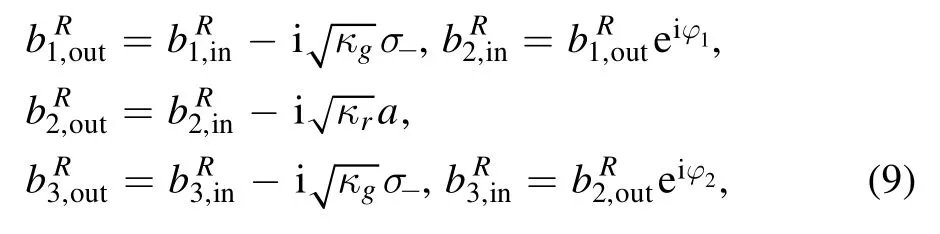
φ1,2is the phase shift arising from the separation distance d1,2.It satisfies φ1,2=k(ω)d1,2,where k(ω)describes the dispersion relation.The field toward left is similar.It should be noted φ1,2is determined by the giant atom’s frequency.For example,φ1=π/2 means the separation between the first and second connection point is λg/4,where λgcorresponds to the wavelength of ωg.
Using the left-right propagating field and the singlephoton scattering model to simplify equations (7),(8),we have
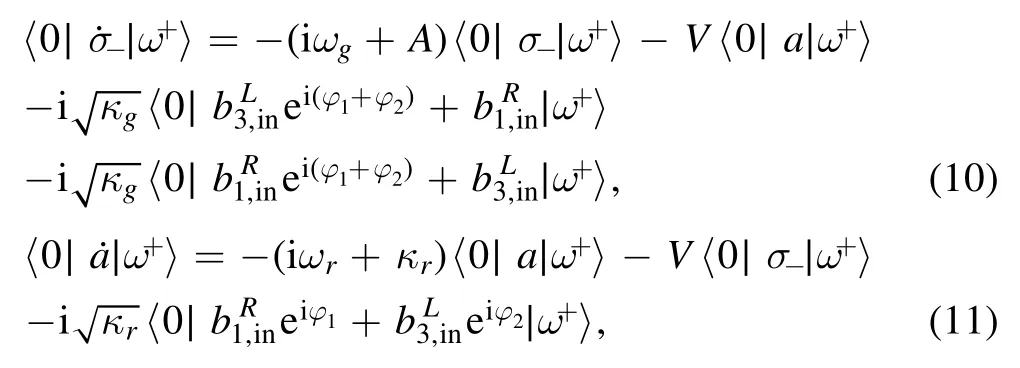

From equation (9) and the left propagating one,we can obtain the input–output relations as
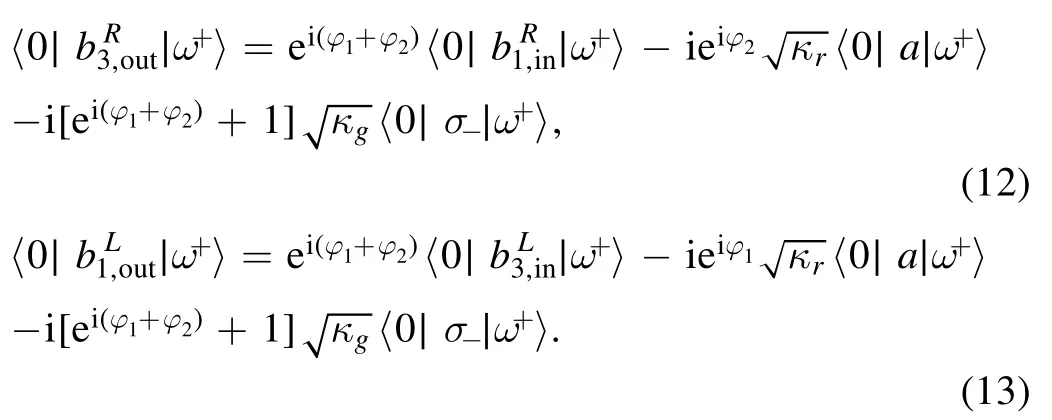

5.Transmission spectroscopy
In this section,we classify the transmission spectra into three types by waveguide-mediated interaction parameter V.We will analyse the transmission spectra,compare the results with other coupling regimes,and introduce some applications.A similar work is in [28].
5.1.V is an imaginary number
We first consider φ1,2=π/2 withbeing an imaginary number.As confirmed in experiments,the giant atom can be protected from decoherence= 0[14].However,the waveguide-mediated interaction will lead to some interesting interference effects.The transmission coefficient is
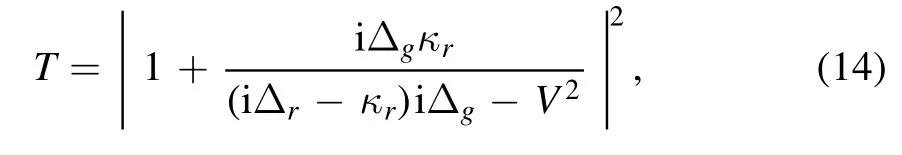
where Δg=ωg-ω is the frequency detuning between the giant atom and the probe field,Δr=ωr-ω is the frequency detuning between the resonator and the probe field.
Figure 2(a) shows the transmission spectra at κr=κg,where the resonator frequency is tuning across the giant atom.To further characterize it,we keep the waveguide-mediated interaction parameter fixed,changing the ratio of κr/κg.Figure 2(b) describes the resonance regime Δg=Δr.The separation between the transmission peaks is 2|V|,and the spectral lines broaden as κr/κgincreasing.Figure 2(c)shows the non-resonance regime.The asymmetry lines around Δg=0 arise from the Fano-like resonance [6,29],their bandwidth has changed as well.These results indicate we can use the resonator to control the effective decay rate of the giant atom.For example,we can change the frequency detuning between the components,as well as increasing κr.The numerical calculation is in the next section.
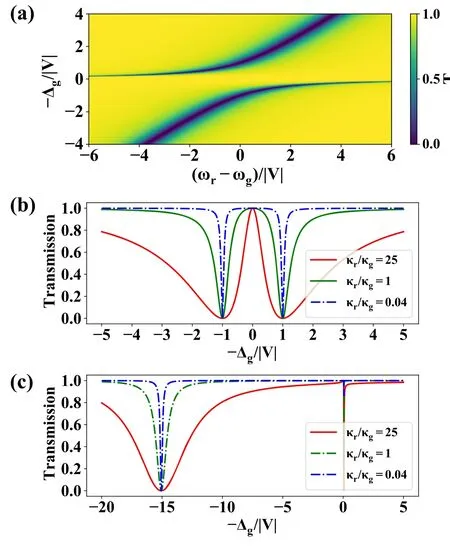
Figure 2.The transmission spectra with φ1=φ2=π/2,the axes are in the unit of |V|.(a) κr=κg.The ordinate axis represents the frequency detuning between the resonator and the giant atom.(b)ωr=ωg.The transmission coefficient with different decay ratio κr/κg.(c)ωr-ωg=-15|V|.The transmission coefficient with different decay ratio κr/κg.
In general,we find these figures are similar to the studies based on the Jaynes–Cummings (JC) model,the JC Hamiltonian is [30]
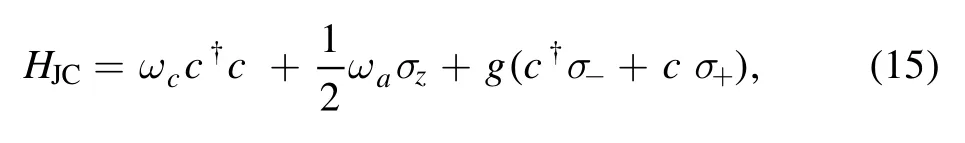
where ωcand ωaare the frequency of the resonator and atom,respectively.c†(c) is the creation (annihilation) operator of the resonator.σzis the Pauli operator of the atom.g is atomresonator coupling strength.Its master equation can be obtained by former studies [31,32].As for our open system,the master equation is
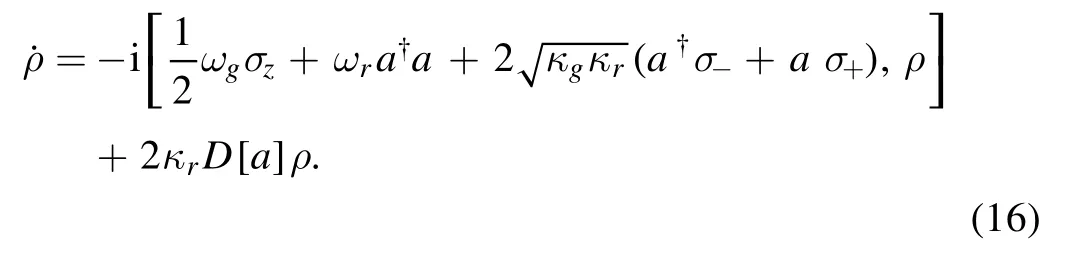
The first line describes the Hamiltonian of our system,which is similar to the direct coupling one.Herecorresponds to g in equation (15).After the comparison,we find these coupling regimes are similar.So we can extend the results in cQED to this waveguide QED system.For example,figures 2(a) and (b) describe the vacuum Rabi splitting between the giant atom and the resonator[28,33–35].We can further use the resonator to obtain the qubit state when the components are far detuned [1].
5.2.V is zero
When φ1=π/2 and φ2=3π/2,the waveguide-mediated interaction parameter becomes V=0,andgets the maximum value= 4κg.The transmission coefficient is
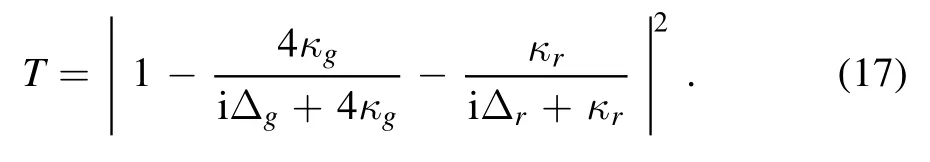
When the components are on resonance ωg=ωr(see figure 3(a)),we can find two transmission peaks,which widen and lighten with the increase of κr/κg.A full transmission is realized at κr/κg=4 (red curve) and vanish as κr/κgfurther increasing.To characterize its difference with the vacuum Rabi splitting,we tune the resonator frequency across the giant atom,as shown in figures 3(b) and (c).The master equation of our system is
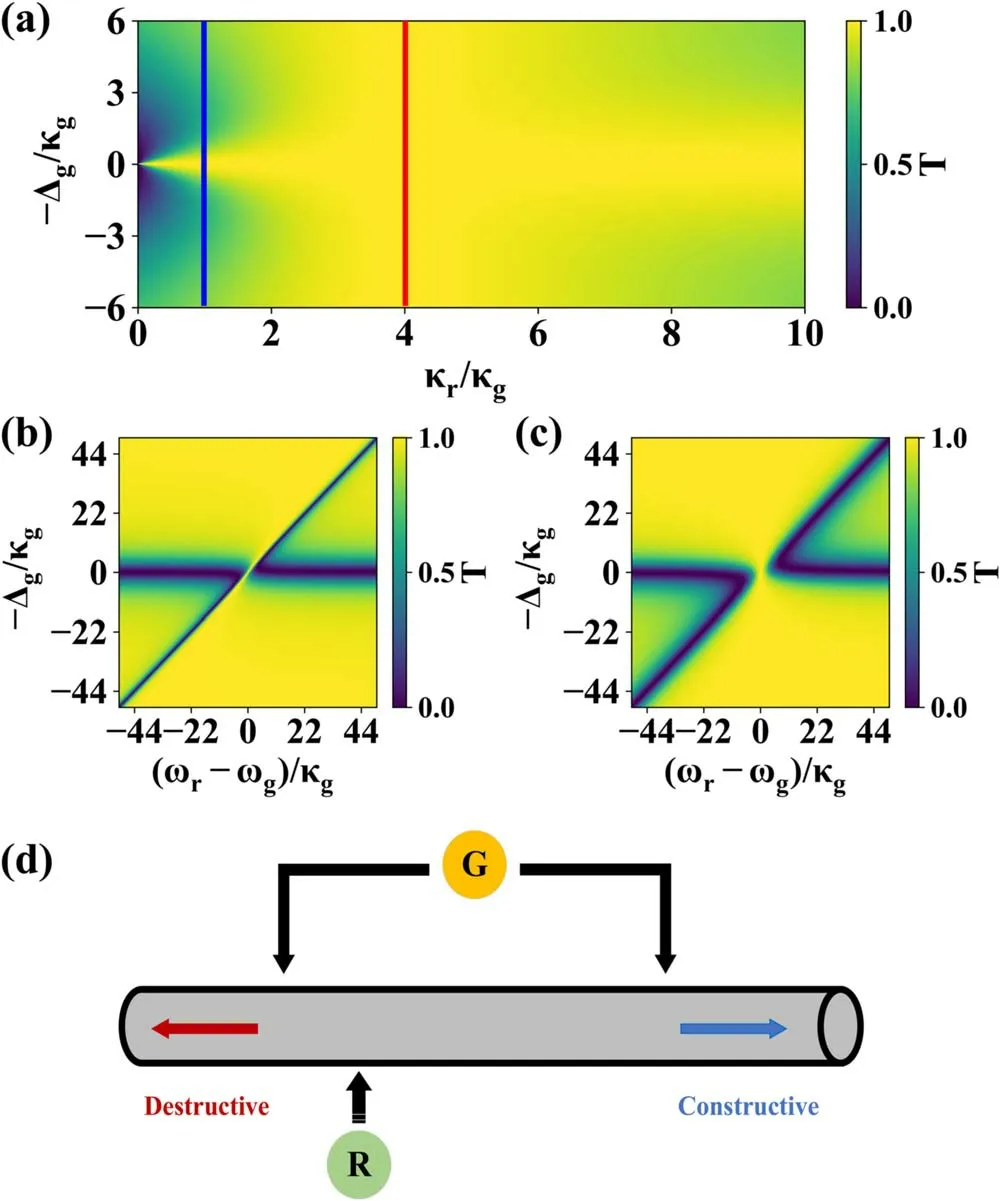
Figure 3.φ1=π/2 and φ2=3π/2.(a) ωg=ωr,the transmission coefficient with different κr/κg.The blue and red curve correspond to κr/κg=1 and κr/κg=4,respectively.(b) κr/κg=1,the resonator is tuning across the giant atom.(c) κr/κg=4,the resonator is tuning across the giant atom.(d) When the components are papered in the entangled statethe interference effect leads the photon propagates towards right (blue arrow).
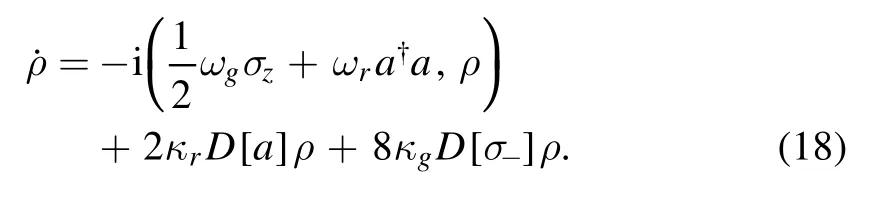
It is similar to a hybrid coupling system,where two qubits connect to the waveguide a quarter wavelength apart,and a direct coupling helps cancel the waveguide-mediated interaction [22,23].Here we generalize the conclusion,introducing the forward (right) decaying mode operator
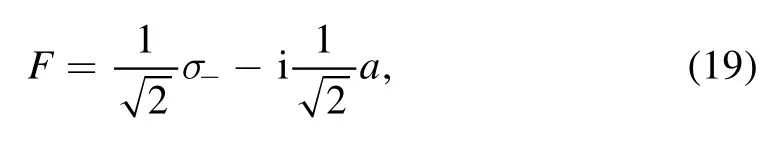
where the backward decay mode is the conjugate of it.Using equations (19) to simplify (10)–(12),the equation of motion and input–output relation of F are

These equations indicate the forward decay mode only couples with the forward traveling modes (and.We can also use them to obtain the transmission coefficient in equation (20).Some related studies in the resonator-waveguide coupling system help better understand it[36,37].Just like the hybrid coupling system,we can use the interference effect to generate the unidirectional transport [22,23].We assume the giant atom and the resonator are in the entangled state
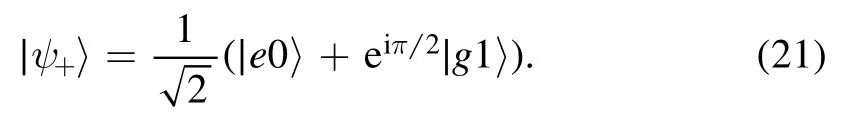
The leftward emission photon,decaying from the resonator,accumulates a π/2 phase shift before it reaches the left connection point of the giant atom.The destructive interference leads the leftward-propagating photon vanish (the red arrow in figure 3(d)).While the rightward emission photon,decaying from the resonator,is on the contrary (the blue arrow in figure 3(d)).So this system has the potential to realize unidirectional transport.Some experiments,based on building non-Hermitian Hamiltonians,can also help realize unidirectional reflectionlessness.While they add an internal loss item to the Heisenberg equation of motion [38,39].
5.3.V is a real number
In this section,we assume φ1,2=π with V being a real number.The individual decay rate of the giant atom is= 4κg,and the transmission coefficient can be expressed as
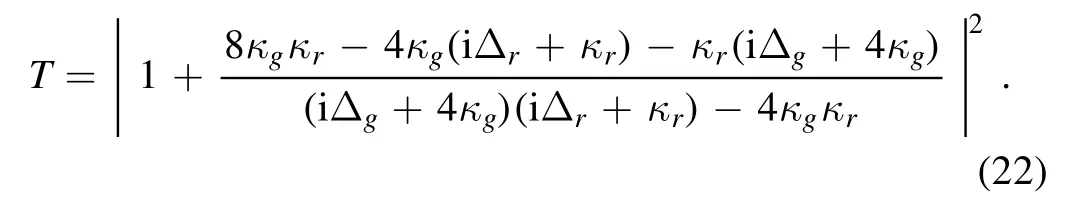
When the components are on resonance ωg=ωr,there is one transmission peak.The variation of κr/κgonly changes its bandwidth,as shown in figure 4(a).The master equation for our system is
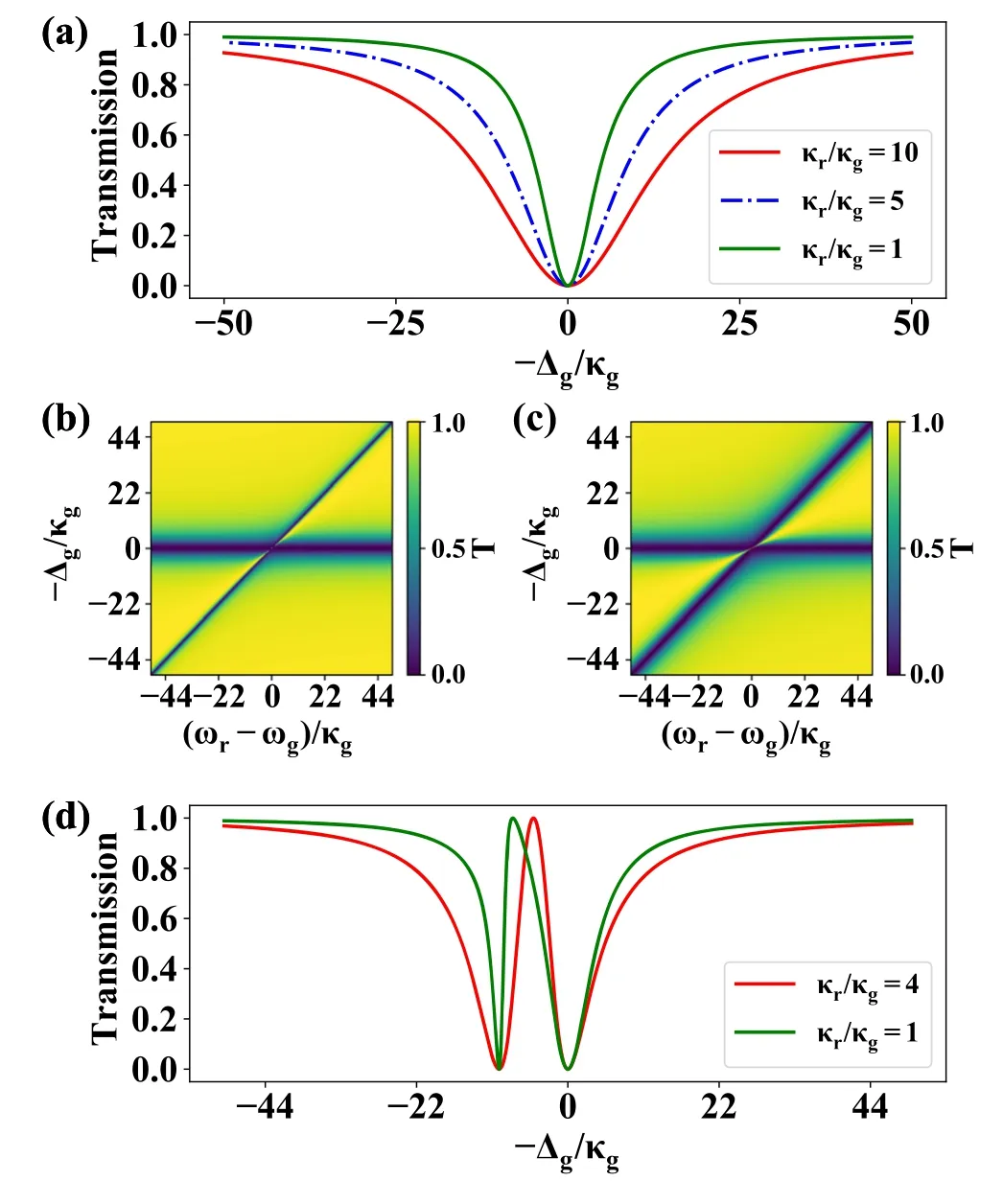
Figure 4.The transmission spectra with φ1=φ2=π.(a) ωg=ωr,the transmission coefficient with different κr/κg.(b) κr/κg=1,the resonator is tuning across the giant atom.(c) κr/κg=4,the resonator is tuning across the giant atom.(d) Δg/κg=10,the transmission coefficient with different κr/κg.
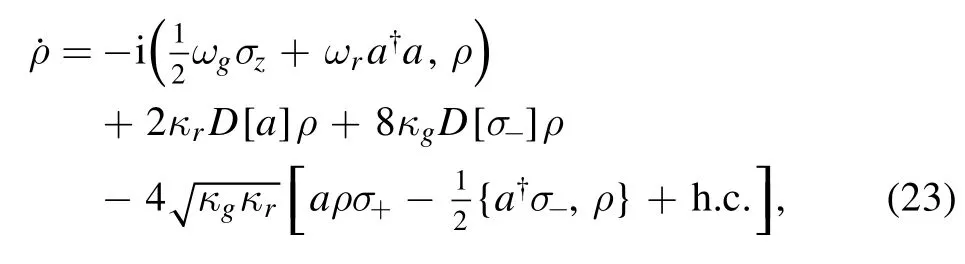
which is similar to small atoms with half wavelength apart[8,24].The last term in equation(23)describes the collective decay effect.When κr/κg=4,it corresponds to the superradiant process in the atom-waveguide coupling system [10,24].
When the resonator is detuned from the giant atom,as shown in figures 4(b) and(c),we can find a transparent peak between ωgand ωr.For the case of κr≈4κg,the peak locates in the middle of the two resonance frequencies,which can be explained by the EIT effect.In other situations,the peak locates near the narrow mode,and this is from the Fano resonance (see figure 4(d)) [6,7].These interesting interference effects helps reduce the group velocity of the microwave,which holds the promise for application in quantum storage and quantum information.
6.Decay rate
In a direct atom-resonator coupling system,the atom suffers a decay losses via the resonator.This effect is found by Purcell and has been observed in many systems [2].We assumein equation (15) and the resonator decay rate is 2κr.The atom decay rate by Purcell’s theory is given by[2–4]
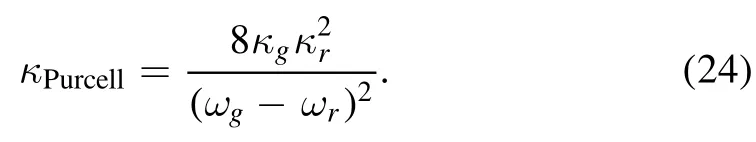
Now we explore the effective decay rate κeffof the giant atom.We firstly assume the input fields are in the vacuum state andκ≫In the single-excitation subspace,the evolution of the resonator is faster,and thus it is in the steadystate 〈˙a〉 =0.Under the rotating wave approximation,we can obtain the expression of 〈a〉 by equation (11)
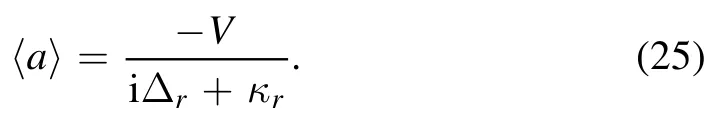
Insert 〈a〉 to 〈˙σ〉-(obtained by equation (10)),we get the equation of motion for the giant atom.The real part determines its effective decay rate
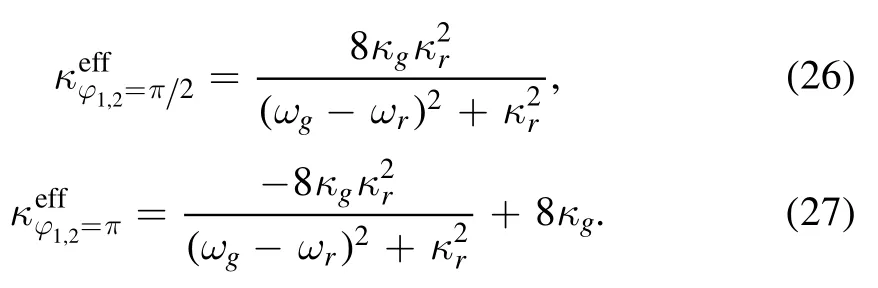

7.Conclusion
In conclusion,we place a giant atom and a resonator to the waveguide,investigating the interference effect between them.The transmission spectra show different characteristics.In the resonance regime,we find the vacuum Rabi splitting,total transmission,and the superradiant-like state.When the components are detuned,we can observe the EIT or Fano resonance.These effects have applications in the waveguidemediated quantum gate,unidirectional transport,and atom decay suppression.Looking forward,our approach can be extended to a larger quantum network,which has the potential in exploring many-body physics.
Acknowledgments
This work was supported by the NKRDP of China(Grant No.2016YFA0301802),NSFC (Grant No.61521001,No.12074179 and No.11890704),and the Key R&D Program of Guangdong Province (Grant No.2018B030326001).
杂志排行
Communications in Theoretical Physics的其它文章
- How polar hydroxyl groups affect surface hydrophobicity on model talc surfaces
- Optical soliton in a one-dimensional array of a metal nanoparticle-microcavity complex
- Impurity effects of the Λ hyperon in the hypernuclear systems Mg and Si
- Constraint on nuclear symmetry energy imposed by f-mode oscillation of neutron stars
- Wormhole solutions and energy conditions in f(R,G) gravity
- Valley-resolved transport in zigzag graphene nanoribbon junctions
