基于部分三阶邻居信息的一致性算法

严志强 葛磊 张跃跃 窦磊

1.南京理工大学瞬态物理国家重点实验室南京210094

多智能体系统控制在近些年发展迅速,广泛应用于无人机编队、传感器网络、机械臂装配、多导弹的联合攻击等领域[1-2].因此,一致性问题成为多智能体系统研究中的核心问题.一致性[3]的定义为:随着时间的演变,多智能体系统中的所有个体的某一个或者几个状态趋于一致.一致性协议是人为规定的智能体之间的通信原则,它描述了各个智能体与其他智能体的通信规则和通信过程.

本文研究的三阶多智能体系统具有一定的工程意义.对加速度求导得到急动度,也称为力变率,用以描述加速度变化率.特别地,在交通运输设计上往往需要急动度来解决问题.例如:汽车工程师可用急动度作为衡量乘客舒适度的指数[4];Lorens 通过特殊的变形后,即用具有一个独立变量的三阶微分方程描述问题,可以把蝴蝶效应变成一个类似的一维突变运动;JW2-3D 型加加速度计主要用于强地震观测等等.此外,三阶系统在日常生活和工程中又是常见的,其性能指数比较复杂,因此,三阶多智能体系统的研究有着十分重要的意义.

学者们最早研究的是一阶多智能体系统,结果颇多，理论相对完善,其中具有代表性的是2004年Olfati-Saber 等[5]研究的一阶多智能体系统在切换网络拓扑下的一致性问题,该文献在一致性问题研究上具有开创性意义,为多智能体一致性问题研究奠定了基础.在二阶多智能体一致性问题研究上,目前也取得了大量研究成果.例如,2007年,Sun 等[6]研究了二阶多智能体系统在拓扑分别为固定和切换的条件下的均匀一致性问题;2009年,Lin 等[7]探究了带有不均匀时滞的离散时间二阶系统在动态交换拓扑条件下的一致性问题;2010年,Yu 等[8]探究了在有向图的假设条件下带时滞和不带时滞的二阶系统一致性问题等.

对于三阶多智能体系统,许格升等[9]研究了在有向图中,利用分段连续可微的向量表示理想时变编队,将编队问题转化为一致性问题,再通过使用复系数的Hurwitz 多项式证明了三阶系统设计编队的充要条件;董滔等[10]研究了基于事件触发控制的三阶离散多智能体系统,利用位置、速度和加速度的测量误差,设计了具有创新意义的事件触发控制机制,然后通过不等式运算给出了多智能体系统达到一致的充分条件;文献[11] 针对三阶多智能体系统提出了一种计算控制输入中的加权系数的算法,并通过Hurwitz 多项式证明该系统的一致性;文献[12-13] 研究了三阶时延多智能体系统,通过矩阵理论和Nyquist 准则,着重建立了最大可容忍通信延迟与非零特征值和图拉普拉斯矩阵之间的对应关系.

对于高阶多智能体系统,2006年,Ren 等[14]研究了在有向图中多车辆系统的协同控制一致性问题;2014年,Zhu等[15]探究了高阶系统在切换拓扑前提下的一致性问题等.

目前对于特定三阶多智能体系统的研究还相对较少,并且随着智能体的增加,系统达到一致的时间和通讯线路数量也大大增加,针对这个问题,通过新规定的近邻原则,合理地减少通讯线路,优化系统收敛速度,提出了基于部分邻居信息的一致性算法.

本文安排如下:第1 节对相关图论和矩阵理论作了初步的介绍;第2 节给出并证明了典型三阶一致性算法,并且提出近邻规则,进而得到两种不同的算法,新算法能够加快系统收敛速度,减少通信负担;第3 节为了验证理论结果,进行了三种算法的仿真并给出数值比较;最后,第4 节对全文进行了总结.

1 基础知识

图论是一致性算法研究的基础知识.一个加权的有向或无向图G定义为G=(V,E,A),其中,V={v1,···,vn}是节点集,E ⊆V ×V是一组边,用来描述多智能体之间的联络关系.此外,n是节点数目,属于边集合E的eij,定义为eij=(vi,vj)∈E,其中,vi表示边E的起始端,vj表示边E的末端,图可以分为两类,有向图和无向图.如果图的边是有向的,则图是有向的.那么(vi,vj)∈E ／=(vj,vi)∈E,则eij=(vi,vj)表示第i个智能体向第j个智能体传输信息;如果拓扑图的边是无向的,那么图是无向的,那么(vi,vj)∈E=(vj,vi)∈E,则eij=(vi,vj)表示第i个智能体与第j个智能体之间互相传输信息.

2 一致性协议与分析

2.1 一致性协议

2.2 一致性分析

2.2.1 TNI 分析

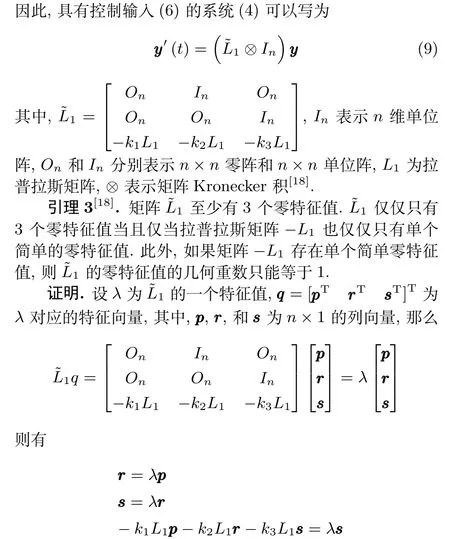
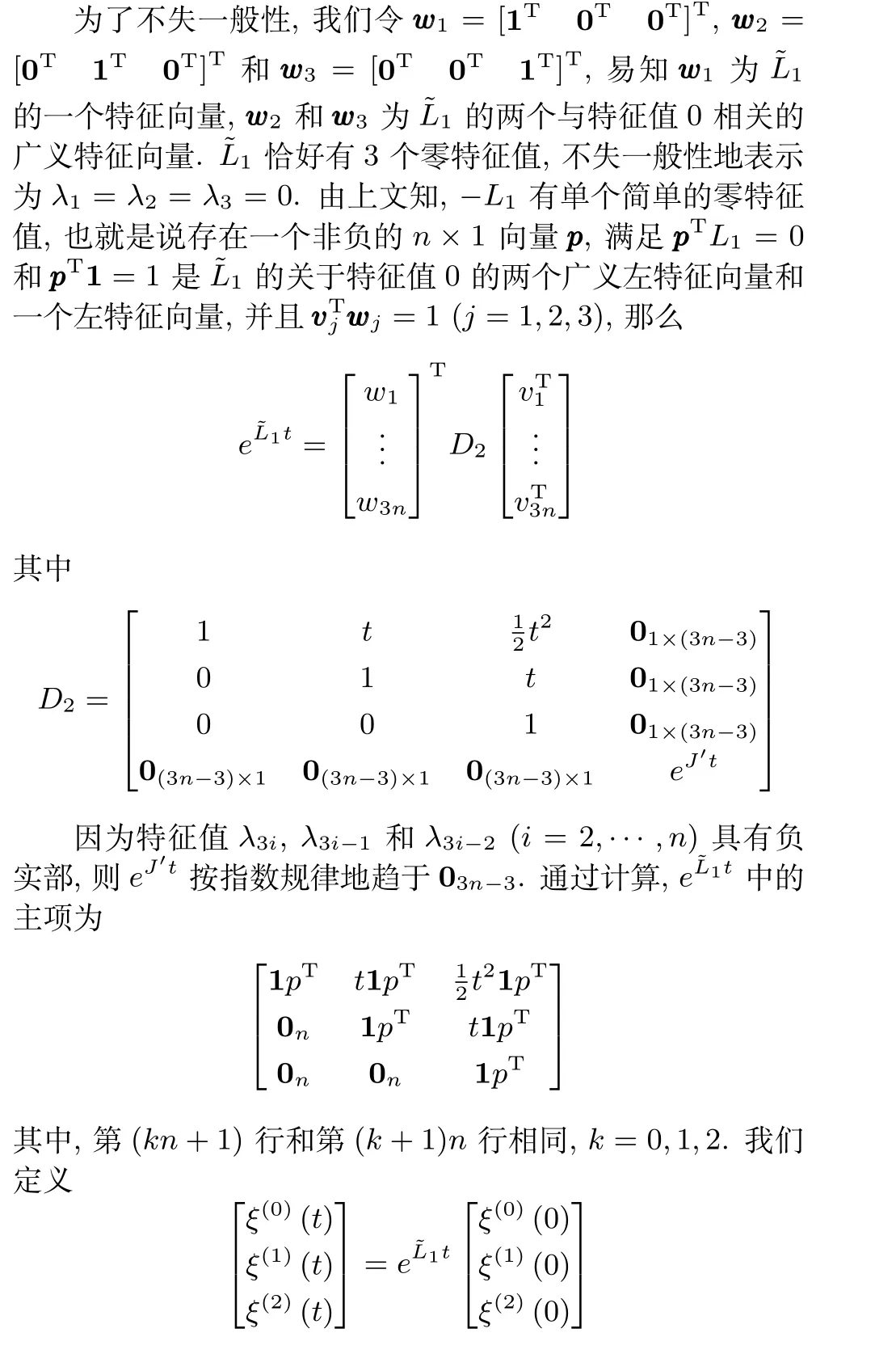
图1 与图2 是TNI 算法所对应的无向通信拓扑,图1 中实线连接的两个节点互为一阶邻居节点,虚线连接的两个节点互为二阶邻居节点,图2 实线连接的两个节点互为三阶邻居节点.其对应的拉普拉斯矩阵为

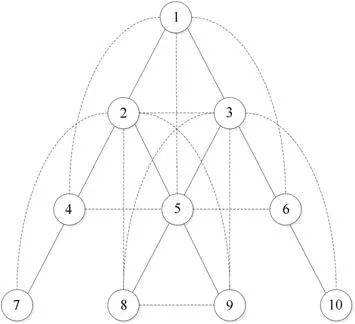
图1 TNI 一阶与二阶通信拓扑Fig.1 TNI first-order and second-order communication topology

图2 TNI 三阶通信拓扑Fig.2 TNI third-order communication topology

2.2.2 PTNI 分析

具有控制输入(7)的系统(4)可以写为

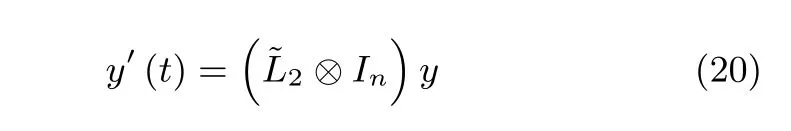
对于系统(20),在TNI 通信拓扑图的基础上,不改变一阶与二阶通信拓扑,通过近邻规则去除了部分三阶通信线路,去除方法如下.

图1 和图2 给出了一阶、二阶和三阶通信拓扑图,图3是对应的PTNI 算法,我们通过近邻原则去除了部分三阶邻居通信线路.

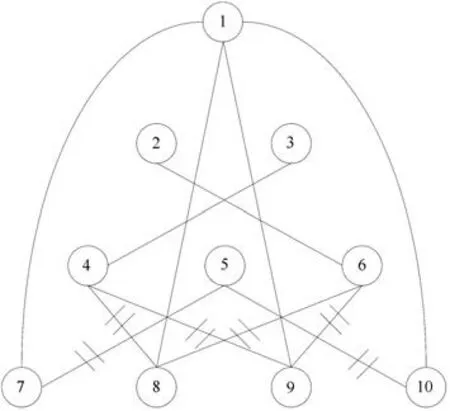
图3 PTNI 部分三阶通信拓扑Fig.3 PTNI part of third-order communication topology

三阶近邻原则为:越位于上层的智能体就越重要,每个智能体都会与智能体1 进行通讯,在其他智能体与1 通信时会优先选择复杂度最低的路线.在图3 中,智能体7 的三阶邻居为1 和5,7 在与1 进行通讯的时候,就不会通过5 再与1 进行通讯,智能体10 同理;再例如,8 的三阶邻居为1,4,6,首先8 会优先选择直接与1 通信,舍弃与4,6 之间的通信,智能体9 同理.

其对应的拉普拉斯矩阵为

2.2.3 PPTNI 分析

具有控制输入(8)的系统(4)可以写为

对于系统(21),在PTNI 通信拓扑图的基础上,不改变部分三阶通信拓扑,通过近邻规则去除了部分二阶通信线路,去除方法如下.

图3 和图4 是PPTNI 算法所对应的无向通信拓扑,我们通过近邻原则去除了部分二阶与三阶邻居通信线.

图4 PTNI 部分二阶通信拓扑Fig.4 PTNI part of second-order communication topology

二阶近邻原则为:越位于上层的智能体就越重要,每个智能体都会与智能体1 进行通讯,在其他智能体与1 通信时会优先选择复杂度最低的路线,当某一智能体与另一智能体进行通讯,并且存在多条复杂度相同的通讯线时,只会选择其中一条进行通信.在图4 中,智能体4 的二阶邻居为1 和5,4 在与1 进行通讯的时候,就不会通过5 再与1 进行通讯，智能体6 同理；再例如，8 的二阶邻居为2,3,9，首先8 只会优先选择上层邻居进行通信而舍弃同层邻居9，在与上层邻居2,3 通讯的时候,8 会优先选择2 进行通信,然后通过2与1 进行通信l,而不会选择越过5 与3 通信再与1 通信,智能体9 同理.

其对应的拉普拉斯矩阵为

3 一致性仿真

在这部分,我们将根据上述通信拓扑给出数值例子,通过仿真检验所提算法的性能.通过推论1 给出可调参数k1=0.3,k2=1 和k3=1,模拟的初始位置、速度和加速度如下:

使用给出的数据,分别得到TNI、PTNI 和PPTNI 仿真图，如图5～7所示.

图5 TNI 仿真图Fig.5 Simulated diagrams of TNI

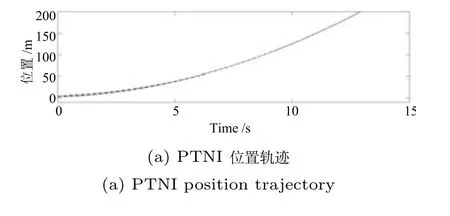
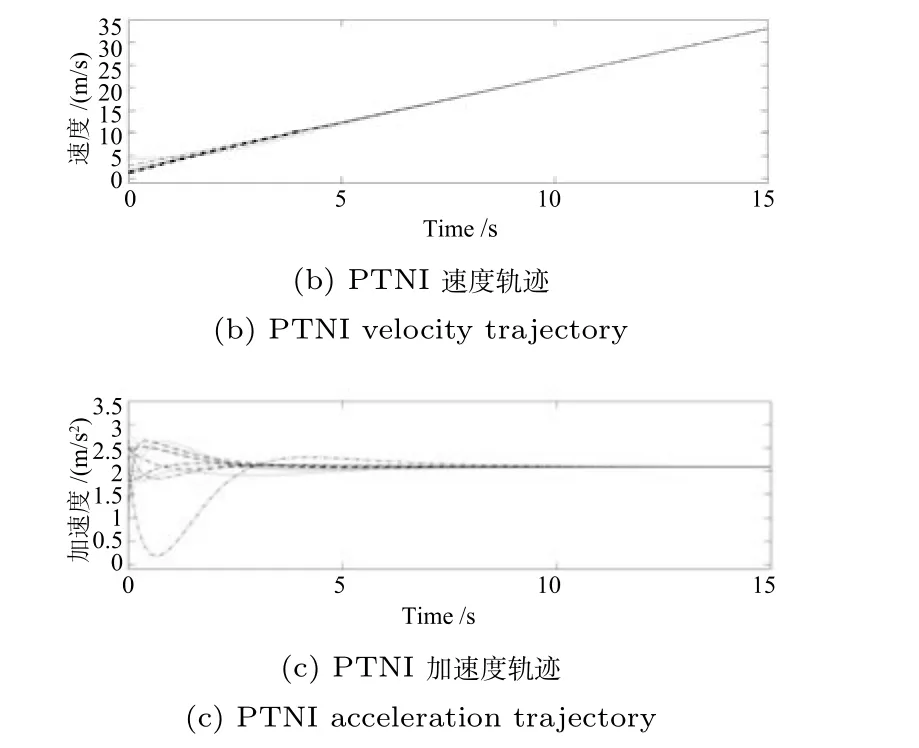
图6 PTNI 仿真图Fig.6 Simulated diagrams of PTNI

图7 PPTNI 仿真图Fig.7 Simulated diagrams of PPTNI

由仿真结果可知,三种算法均能够使系统(4)在有限时间内快速达到一致性并且性能稳定,验证了算法的可行性和有效性.上述仿真数据列如表1所示.

表1 收敛速度达到一致的时间(取值误差为1%)Table 1 Times that the convergence speed achieves consensus

在表1 中,分别列出了应用三种算法的多智能体系统达到一致的最小时间,最大时间和平均时间.通过表中数据可以明显看出,使用部分三阶邻居信息算法(PTNI)的系统的一致收敛速度比使用典型三阶邻居信息算法(TNI)的系统的一致收敛速度要快,前者的通讯线路数量从35 减少到29,减少率为17.14%,当通信拓扑图更为复杂时,后者达到一致的平均时间将明显比前者小的多;此外,使用部分二阶与三阶邻居信息算法(PPTNI)的系统的收敛速度比典型三阶邻居信息算法(TNI)和部分三阶邻居信息算法(PTNI)的系统的收敛速度都要快,并且其通信边缘数量从35 减少到24,减少率为31.43%.当系统更为复杂时,PTNI 算法和PPTNI算法达到一致性的时间将减少得更为明显.

由此可见,在实现多智能体系统一致性的前提下,部分三阶邻居信息算法(PTNI)和部分二阶与三阶邻居信息算法(PPTNI)加快了三阶系统一致性达成速度,提高了系统的效率,并且优化了通信线数量,降低了实际成本.

4 结束语

在连通但不相关的通信拓扑图设定下，本文考虑了多智能体一致性算法中的通信问题.基于典型三阶邻居信息一致性算法(TNI),我们提出了二阶和三阶近邻原则，进而设计了部分三阶邻居信息算法(PTNI)和部分二阶与三阶邻居算法(PPTNI).实验结果表明:TNI 算法可实现多智能体系统的一致性,解决了一致性问题;在此基础上,PTNI 和PPTNI收敛速度均快于TNI,并且通讯代价也大大减少.这说明PTNI 和PPTNI 算法能够发挥优化作用,在提高系统的响应速度的同时,也降低了实际成本.