基于自学习中枢模式发生器的仿人机器人适应性行走控制

刘成菊 耿烷东 张长柱 陈启军

1.同济大学电子与信息工程学院上海201804

仿人机器人具有双手、双足、躯干等人类外形特征,无需改造就能适应人类日常环境和使用工具,更容易成为辅助人类生活、工作和完成危险作业的帮手,因此可认为是下一代服务机器人最典型、最友好的本体特征.行走控制是仿人机器人的基础科学问题,但仿人机器人自由度多、传感器多,是一个不稳定的非线性强耦合动力学系统,行走的自然性、环境适应性、突发环境变化时的平衡控制是长期困扰仿人机器人发展和应用的难题.目前,行走控制方法主要基于编程作业机制,使得仿人机器人的本体特性不能得到充分的发挥[1].普遍采用的基于零力矩点(Zero moment point,ZMP)的步行控制方法[2-7],允许机器人按照预先设计的轨迹行走并保持平衡,但是由于预先设计的轨迹是固定的,一旦地形发生变化,则机器人无法完成行走任务.对于机器人的环境适应性行走控制,需要具有自适应产生轨迹的能力.

改变传统的思维模式,研究和抽象生物的行走机理并加以模仿,可能是突破机器人行走控制瓶颈的有效途径.该思想也引起相关学者的广泛关注,其中,比较著名的方法是基于中枢模式发生器(Central pattern generator,CPG)的生物诱导的机器人行走控制方法[8-13].由于其突出的适应性优势已经广泛应用在机器人运动控制中,特别是在游泳、爬行、多足机器人的运动控制中取得了成功实验效果[14-21].然而目前存在的CPG 模型基本只能产生正弦或类似正弦的输出,如Hopf模型[22-23]、Kuramoto 模型[24-25]等.即使存在能够在一定程度上调整输出波形形状的模型,如Matsuoka 模型[26-28],但是模型参数与输出波形的形状之间没有明确的对应关系,只能通过试凑法不断地尝试.并且只能对输出进行简单调整,无法准确模拟某一特定形状.在Righetti 等[29-30]的工作启发下,我们提出了一种基于快速傅里叶变换的自学习CPG(Self-learning CPG,SL-CPG)模型.提出的模型可以学习周期性任意形状输入信号,解决了以往CPG 模型输出上的局限性.自学习CPG 模型可以通过调整参数在线平稳调整其输出频率和幅值,为引入传感器信号提供了便利.

另一方面,如何将CPG 模型应用于机器人的节律运动控制是该研究的另一难点问题.目前CPG机器人生物诱导控制方法应用较多的是关节空间控制法.通常将一个CPG 单元分配给一个自由度,优化CPG 拓扑网络,生成多维协调信号,直接控制关节运动实现运动控制.关节空间方法在爬行、游泳、多足等机器人上取得了突出的研究成果.但是仿人机器人自由度多、结构复杂,如果直接将CPG 分配到机器人关节空间,利用CPG 之间的相互耦合组成CPG 网络,网络庞大,参数众多.一些学者将CPG 和进化算法结合来实现仿人机器人的行走控制[31-34],参数的进化是CPG 产生满足要求控制信号的关键,但参数和CPG 网络的输出轨迹的关系并不直观.部分学者探索在机器人的工作空间来有效利用CPG 的适应性[35-41],取得了不错的实验效果.

基于学者们的前期研究,我们提出了生物诱导的仿人机器人工作空间行走模型.本文中,我们采用自学习CPG 模型在线生成仿人机器人质心和脚掌轨迹.分别利用两组SL-CPG,通过对示例轨迹的训练学习,形成可以在线调制的轨迹生成器.通过传感器测得机器人自身姿态信息作为轨迹发生器的反馈输入,因此可以根据具体的地面环境适应性调节输出轨迹.机器人的行走速度、腿的支撑段和摆动段的时间、迈步跨度和抬腿高度等可以实时地调整,这是实现环境适应性行走的重要前提条件.基于工作空间的方法大大简化了CPG 网络和参数整定,不需要事先获得地形条件信息,也不依赖于地形测量的距离传感器信息.仿人机器人坡面环境适应性行走实验验证了控制系统的有效性.

1 自学习CPG 模型

自学习CPG 模型采用分层式设计:底层为记忆单元,高层为协调单元.记忆单元负责学习关节的参考控制信号,协调单元负责调整各关节的相位关系并完成步态控制.该模型与其他模型的主要区别在于把相位同步和关节的运动模式控制分离开来.将相位振荡器模型(如Kuramoto 模型)作为新模型的协调单元,仅用来产生相位同步的信息.而把关节的运动模式控制作为记忆单元单独进行设计.产生的关节控制信号不仅可以保证相位锁定还能实现各种关节运动模式.而记忆单元采用傅里叶级数的思想,用有限次的谐波去逼近一个周期函数,学习过程采用Hebbian 学习方法,可以在线学习任意输入,并能够把学到的信息储存起来,通过协调单元的调节作用,产生合适的输出.

1.1 自学习CPG 原理

任意一个周期函数都可以按傅里叶级数展开为

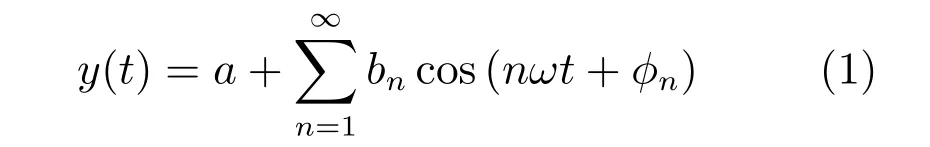
其中,a是常数项,ω是基波的角速度.a和ω很容易计算得到.去掉直流分量整理为

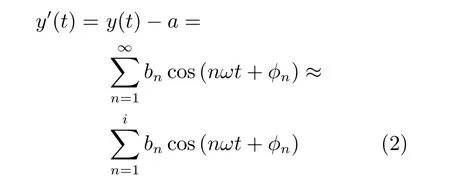
其中,i是整数,i ≥1.因此bn和φn如果确定,那么前i个谐波和就可以用来近似y′.

自学习CPG 的基本思想如图1所示.每个圆代表具有自学习能力的谐波.y′代表需要学习的示例轨迹,P代表系统的输出,F是y′与P的差值.随着学习训练的进行,P将逐渐趋向于y′,F趋向于0,由于忽略了高次谐波,F最终不会为0.但是如果采用足够多的谐波,F将足够小,可以近似于0,此时对系统的影响可以忽略不计.这也就意味着系统的输入和反馈可以切断,系统的输入为0,学习过程停止,系统变为一个自治的系统,系统的输出P虽然和y′有轻微变化,但非常接近y′.基于此,CPG模型可以学习和生成任意周期性信号.

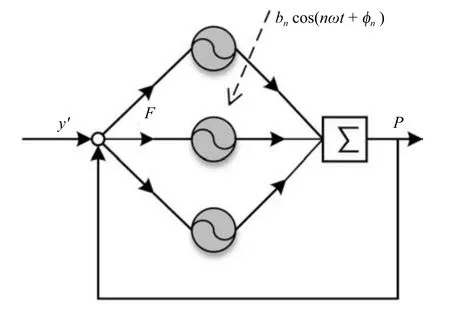
图1 自学习CPG 模型学习基本过程Fig.1 Basic learning process of SL-CPG model

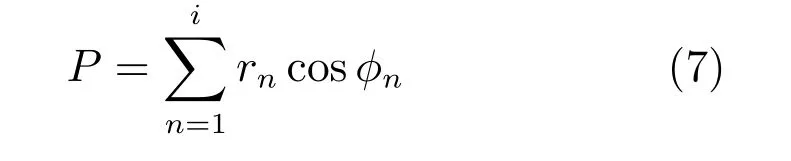
1.2 CPG 模型数学描述

1.2.1 Hopf 振荡器模型

Hopf 振荡器易于独立调节波形的幅值和频率,因此本文采用Hopf 振荡器设计自学习CPG 模型,Hopf 振荡器描述如下:

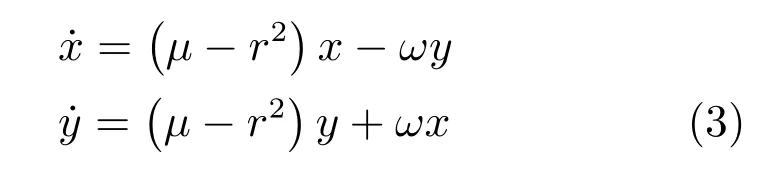
1.2.2 幅值学习

在Hopf 振荡器模型中加入一个扰动项εF,则式(3)变为

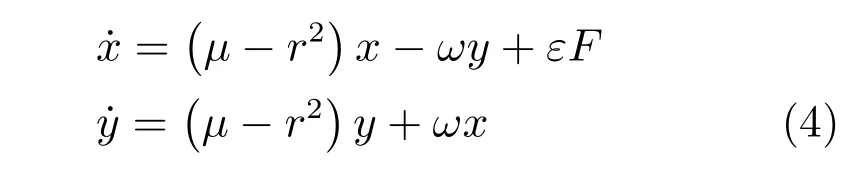
其中,F=P -y′,ε为常数.进行变量替换,令x=rcos(t)和x=rsin(t),式(4)变为

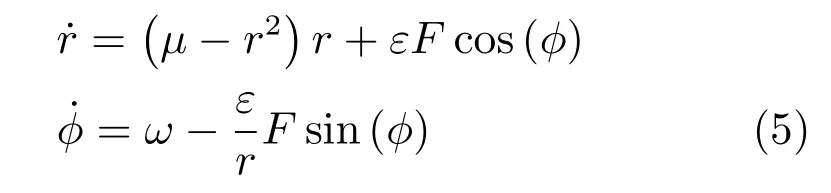
观察式(2),需要确定的变量就是幅值a和相角nωt+φn.而在式(5)中,μ控制幅值,φ是极坐标系下极角变量,相角可以直接通过φ得到.对于如何得到μ,我们借助于Hebbian 学习,设计了一个新的变量α来取代μ,使得α也变成一个动态项,来学习输入信号的幅值,如式(6)所示.

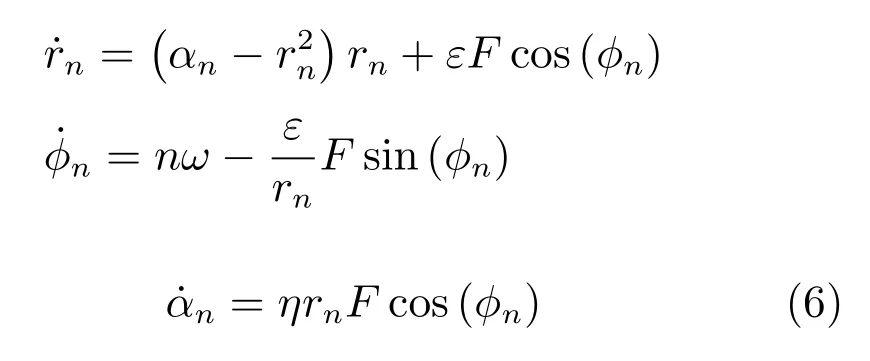
其中,η是学习率,ω是基波角速度,可以通过对输出信号y′进行快速傅里叶变换得到,n代表第n次谐波.最终采用式(6)完成对周期性信号y′的学习,系统的输出如下:

1.2.3 保持模型内相位同步

经过上面的步骤,已经得到了一个能够学习任意周期波形的模型,但这只是一个最基本的模型,要实际应用还需要进一步改进.主要的问题在于:无法调整该模型输出波形的相位.我们不仅要控制一个关节,而是要同时控制多个关节并协调它们之间的相位使之满足一定的步态.因此,如果不能调整任一输出的相位,模型间是不能协调工作的,也就不能用来控制行走.所以,单个模型必须能够根据上一层的控制信号改变输出波形的相位.

根据设计的模型,每个输入都是由一组谐波叠加进行逼近的,当学习结束时,这组谐波之间其实也形成了一定的相位关系.如果在上层控制信号发出改变输出波形相位的命令后,这个相位关系还能够一直保持,那么就能保证调整相位后,输出波形的形状不变.因此,首先要记录这个学习到的相位关系,另外,还要能够保持这个相位关系.

定义θn=φn-nφ1,θn表示学习完成以后第n次谐波与基波之间的相位差.当F设置为0 之后,θn将不再发生变化.采用Kuramoto 模型的方法,此时学习结束后的模型为

当有高层信号使得基波相位发生变化时,其他谐波相位也会立刻跟随基波相位发生变化,最终保持之前的相位关系.因此叠加之后的波形除了相位产生了平移,波形形状保持不变.

1.2.4 保持模型间相位同步

通过加入Kuramoto 项,保持了谐波与基波间的相位差,当基波相位发生变化时,各次谐波的相位能进行跟随,因此保证了模型能够输出正确的波形.为了保持各自学习CPG 之间的相位差,也就是各模型间的相位差,只需要另外加入Kuramoto 项,使相互有连接关系的模型基波之间保持一定的相位差.

1.3 自学习CPG 的参数调制

当自学习CPG 模型完成对示例信号的训练学习后,模型成为一个自治系统.在式(8),αn和ω分别影响CPG 输出的幅值和频率.引入幅值调节系数kα,频率调节系数kω和直流分量调节系数ka如式(9)所示,可以分别独立调节幅值和频率分别为示例轨迹的kα和kω倍,这有利于自学习CPG 根据不同控制需求产生适应性的轨迹.

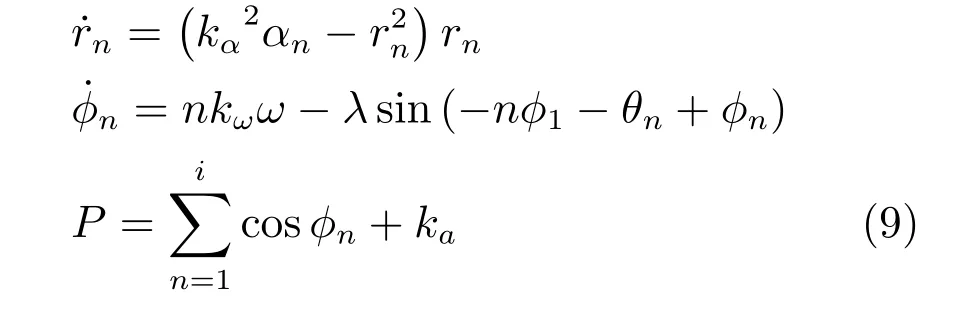
图2 表示自学习CPG 模型对一个示例轨迹的学习情况,其中虚线代表示例轨迹,实线代表自学习CPG 模型的输出.当为t ＜4 s 时为模型学习阶段,当t= 4 s 时,模型学习完成,取消示例轨迹的输入,此时自学习CPG 仍然能够按照示例轨迹的形状继续生成.

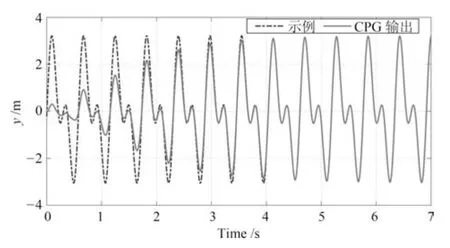
图2 自学习CPG 学习结果Fig.2 The learning results of SL-CPG

图3 表示训练完成后分别调节幅值和频率调节参数调节CPG 的输出.在t= 0～0.6 s,kα= 1 和kω=1,CPG 输出保持和参考轨迹相同的幅值和频率；在t= 0.6～1.6 s,kα=0.5 和kω=1,CPG 输出幅值为参考轨迹的一半,频率相同；在t ＞1.5 s,kα= 1 和kω= 0.5,CPG 输出幅值和参考轨迹的相同,频率是参考轨迹的一半.

图3 自学习CPG 参数调制Fig.3 The parameters modulation of SL-CPG

2 控制系统设计

本文提出的仿人机器人适应性行走的控制系统的整体构架如图4所示,自学习CPG 轨迹发生器包括质心、脚掌轨迹发生器和运动引擎.

图4 整体控制系统构架Fig.4 The architecture of the control system

2.1 质心轨迹发生器

利用自学习CPG 模型对示例的仿人机器人行走时的轨迹进行训练学习,能够得出机器人的三维质心轨迹发生器,质心轨迹在垂直方向上与摆动脚在垂直方向规律一致,CoMz上轨迹由摆动脚轨迹映射得出.这里采取两个自学习CPG 模型来训练学习质心在x和y方向上的运动,为保持轨迹的同步性,两个发生器之间的相位差设为0.图5 和图6 分别表示机器人x方向和y方向的上质心的轨迹,其中虚线表示示例轨迹,实线表示自学习CPG 模型的输出轨迹.

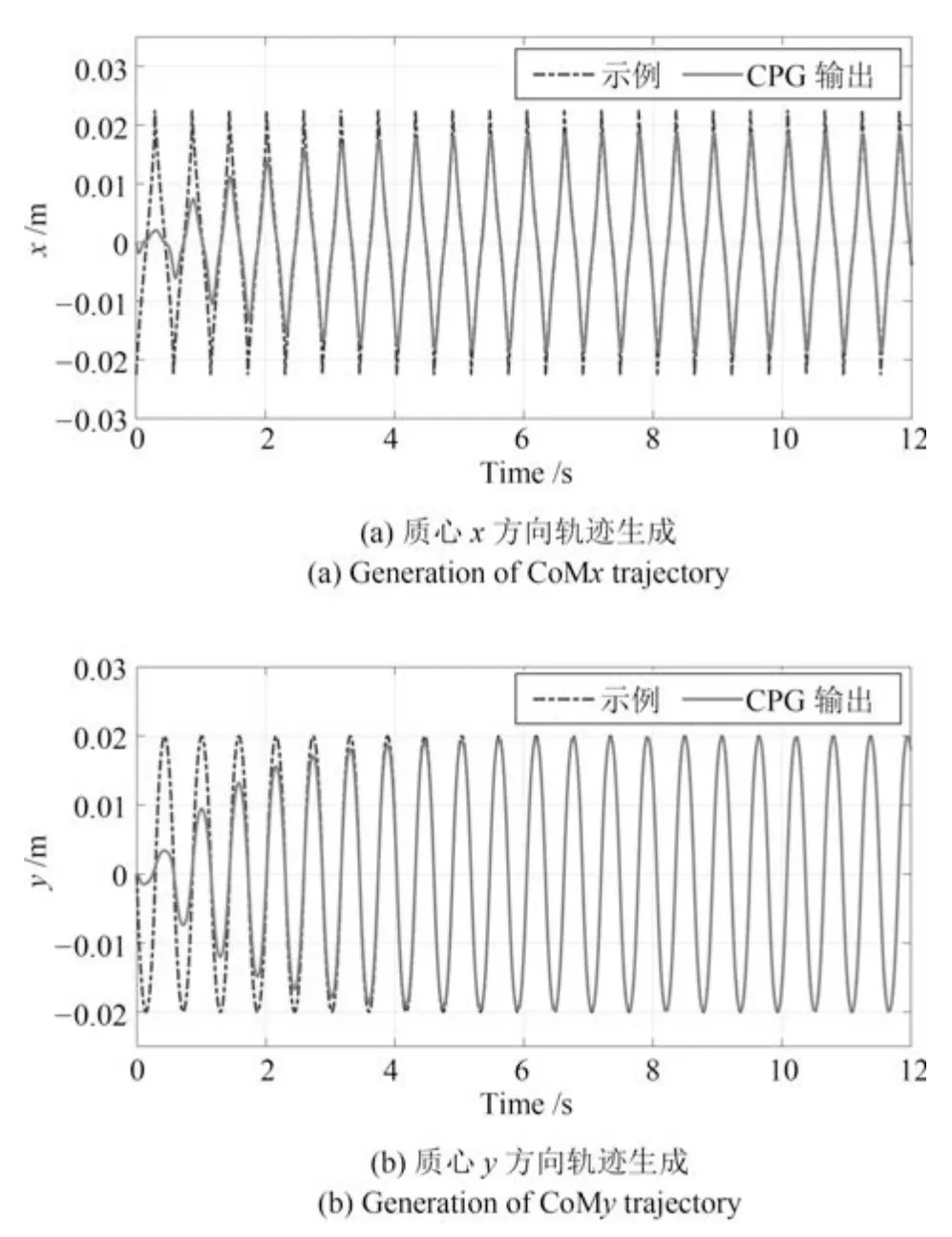
图5 质心x 方向和y 方向轨迹生成Fig.5 The generated CoMx and CoMy trajectories

2.2 脚掌轨迹发生器

机器人在行走时,摆动脚的轨迹在y方向上是恒定的,所以只需要训练两个维度的轨迹.和质心轨迹的训练类似,同样采用了两个自学习CPG 模型,分别在x和z方向上进行训练,这两个方向的幅值分别表示了行走的步幅和迈步的跨度,所以通过调节CPG 的参数,可以很方便地调节机器人行走的上述参数.机器人在行走过程分为左脚支撑阶段和右脚支撑阶段,在每只脚对应的支撑阶段脚掌轨迹为一段直线,自学习CPG 针对连续直线的学习会有较大的误差.

本文采用双脚摆动轨迹联合的改进思路,把双脚摆动轨迹联合,只学习摆动阶段轨迹,然后通过对左右脚支撑的判断,实现双脚轨迹的分离.

图6(a)和6(b)为改进前自学习CPG 模型分别对脚掌轨迹的x和z方向的学习结果,在直线段有明显的误差.图7(a)和7(b)为改进后自学习CPG 模型分别对脚掌轨迹的x和z方向的学习结果,每幅图的上半部是左右脚联合的摆动阶段轨迹,下半部是轨迹分离后单脚的轨迹.其中虚线为示例轨迹,实线为自学习CPG 脚掌轨迹生成器输出轨迹.

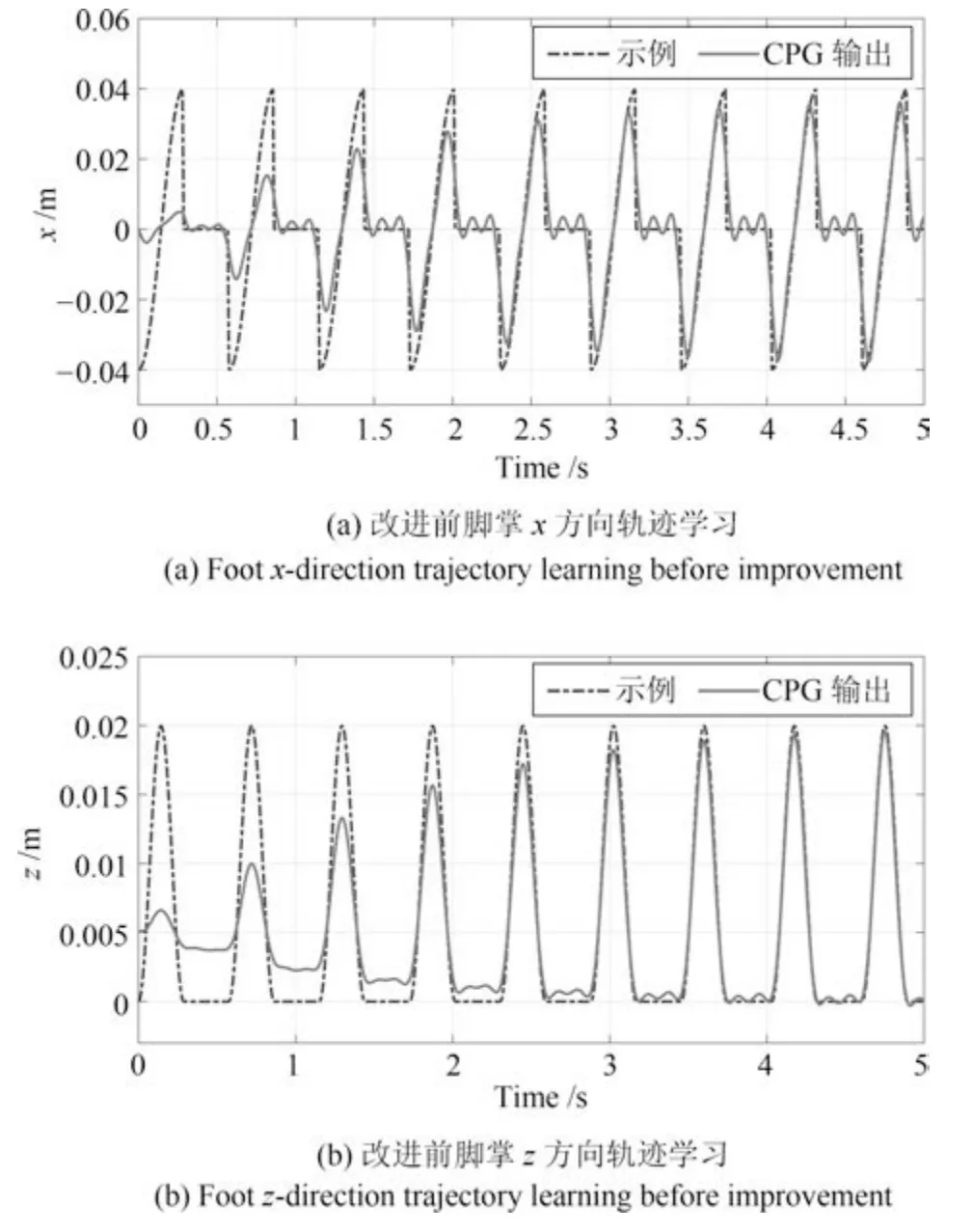
图6 CPG 模型改进前脚掌x 方向和z 方向轨迹学习结果Fig.6 The learning results of the x and z direction foot trajectories before CPG model improved

图7 CPG 模型改进后脚掌x 方向和z 方向轨迹学习结果Fig.7 The learning results of the x and z direction foot trajectories after CPG model improved

2.3 行走适应性

在人类坡面行走过程中,会通过前庭反射来调制姿态,例如身体质心的位置,来避免倾覆.实现机器人环境适应性的关键是如何通过对机器人自身状态和外部环境的感知所获得反馈信息,实现运动控制系统的自我调节.机器人身体姿态角度θpitch可以反映机器人的行走坡面情况,因此以身体姿态角度作为反馈信息实时在线调制CPG 的输出,调整质心和脚掌轨迹的输出轨迹,从而实现仿人机器人的坡面适应性行走控制,反馈设计如图8所示.

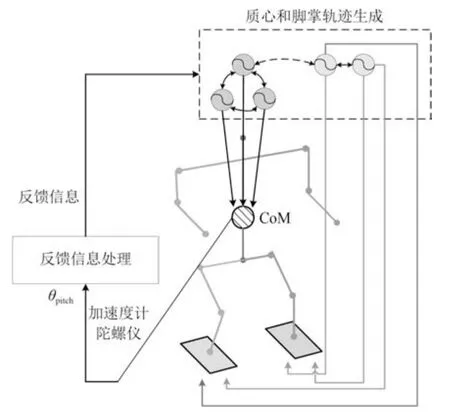
图8 反馈控制回路框图Fig.8 The block diagram of feedback control loop

2.4 运动引擎

在机器人系统中,任务空间与关节空间的关系可描述为

其中,T= [T1···TM]T代表了末端的位置和姿态,而θ=[θ1···θN]T中的θi则表示了连杆i相对于连杆i-1 的转角或位移.

若利用分解速度控制法(Resolved motion rate control,RMRC)[42]来控制关节的角速度,可将机器人系统的微分运动学及逆微分运动学表示为

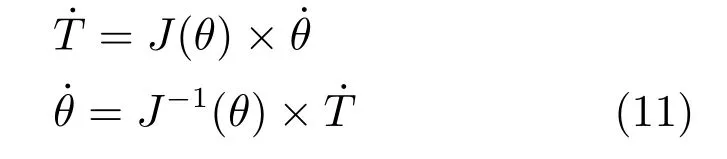
其中,J(θ)为雅可比矩阵,J-1(θ)为其逆矩阵.

如果N ＞M,则机器人系统是冗余的.当雅可比矩阵非满秩时(即系统为冗余时),其逆矩阵不存在,利用伪逆矩阵代替雅可比矩阵的逆矩阵[43]:

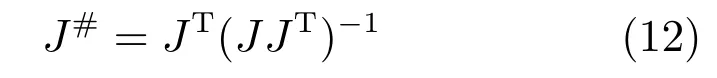
为了防止奇异性问题,可使用最小二乘法表示其伪逆矩阵为

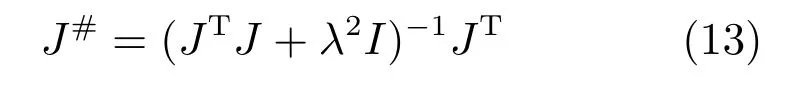
其中,参数λ为阻尼系数,保证雅可比矩阵J(θ)为满秩的.

基于微分逆运动学的机器人运动控制引擎的设计方法如图9所示,其中Tref和Treal代表参考轨迹和实际轨迹,J代表雅可比矩阵,θreal是实际关节角.

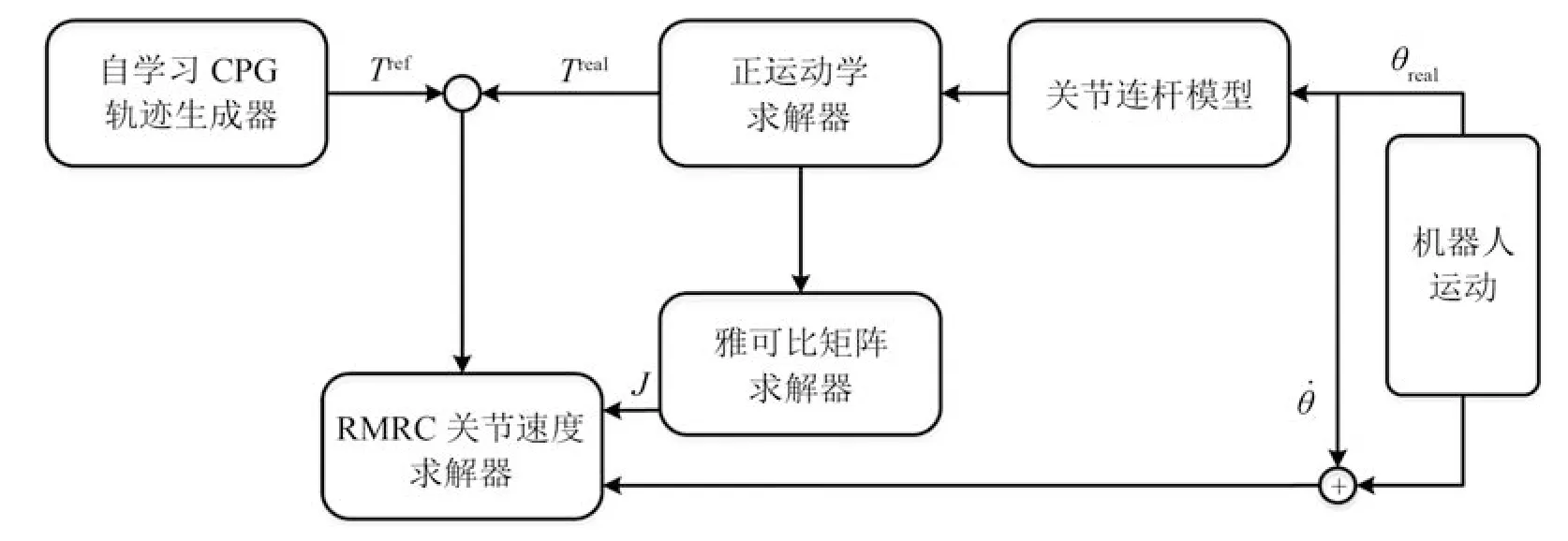
图9 基于微分逆运动学的机器人运动控制引擎设计框图Fig.9 Block diagram of robot motion control engine based on differential inverse kinematics

3 仿真与实验

3.1 反馈回路设计

NAO 仿人机器人作为验证平台.NAO 高58 cm,装有3 轴加速计和2 轴陀螺仪,有25 个自由度,本文只考虑两条腿上的10 个自由度.利用传感器陀螺仪和加速度计均可计算机器人的身体姿态角.加速度计反映的是一种静态特性,而陀螺仪反映的是一种动态特性.由于机器人系统的高频振荡和传感器噪声的影响,计算得到的身体姿态角度不能客观准确地反映机器人的姿态.本文设计了一种补偿滤波器,如图10所示,加速度传感器计算的身体姿态角θacc通过低通滤波器滤掉高频部分,陀螺仪计算出来的身体姿态角θgyro通过高通滤波器滤掉低频部分,再将两者加权求和得到最终的身体姿态角θ

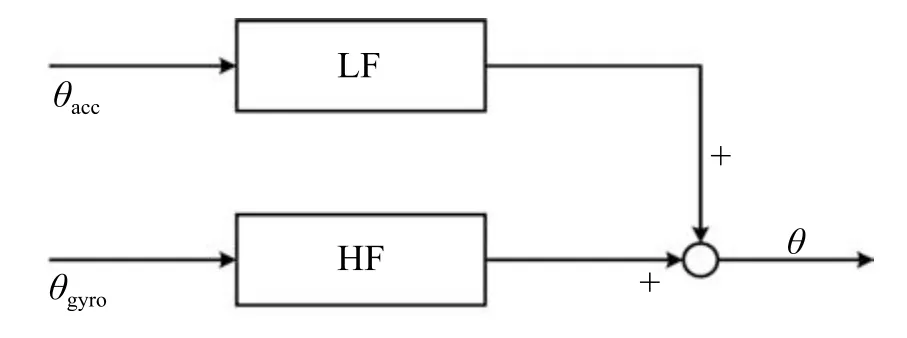
图10 身体姿态角计算Fig.10 Calculation of body attitude

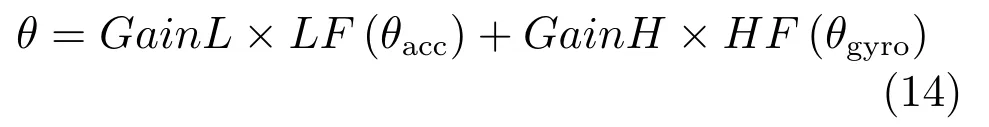
坡面实验环境设置包括上坡、平地以及下坡三种,上下坡面的坡度设定为10°左右.在上坡过程中,机器人质心需要前倾,避免发生打滑;在下坡过程中,机器人应后仰,即质心稍滞后,避免发生倾覆.将身体姿态角作为自学习CPG 产生质心轨迹x方向的反馈信息,设计如下:

3.2 参数优化

为快速获取最佳的反馈控制参数,本节基于Deb 的NSGA-II 算法[44]对控制系统进行优化.本文用到了二元竞争选择,中间交叉和高斯突变等方法,实验的仿真是在Webots 环境下进行.fitnessatti和fitnessdis是设计的两个目标函数来联合优化质心和脚掌轨迹:

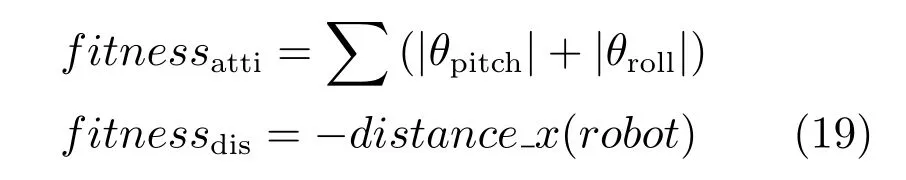
其中,fitnessatti反映了机器人在整个行走过程的稳定性,fitnessdis代表在一次行走中机器人行走的最远距离.

本次实验中NSGA-II 的种群规模为50,最大优化代数为200.优化初期,NAO 在上坡的时候很容易摔倒,经过约40 代的时候,NAO 可以在坡面实现稳定的行走,行走轨迹有可能会偏离直线.图11为进化到180 代的结果,图中标记的点是选择的最优解.表1 中显示了对应的参数,这些参数在实验中均保持相同.

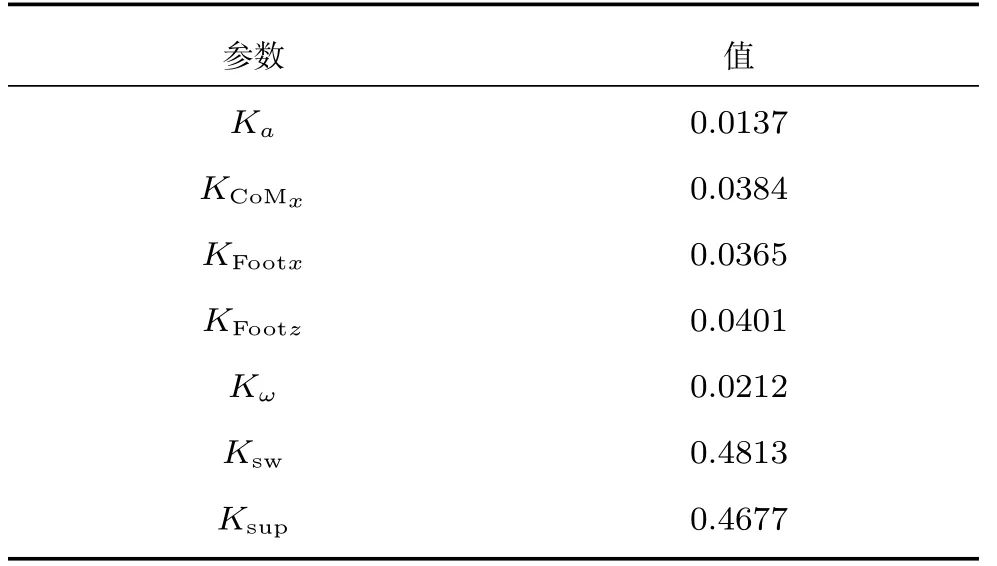
表1 最优参数集Table 1 Optimal parameters set

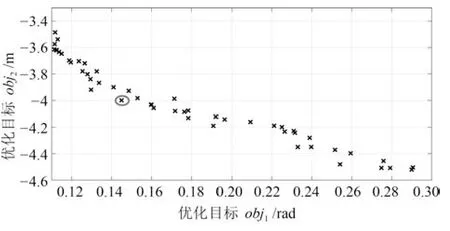
图11 迭代180 次Pareto 前沿面Fig.11 Pareto front of generation 180

3.3 坡面行走

3.3.1 固定坡度坡面行走仿真

仿真实验持续83 s,图12 表示在实验过程中身体姿态角pitch 和roll.图13(a)表明引入身体姿态作为反馈,质心的位置可以在线调制,当走上坡时,CoMx沿斜面向前移动,反之,下坡时质心向后移动.图13(b)所示为脚掌轨迹在线生成的x-z平面轨迹,迈步的高度和长度也根据坡面适应性调整,当上坡时,高度和长度根据反馈信息相应减少防止滑动,反之下坡时相应增加,防止倾覆.图14 是机器人坡面行走时ZMP 的分布情况,其中实线方框代表机器人脚部支撑区域,虚线代表ZMP,整个实验过程ZMP 均保持在机器人的支撑区域内.图15 是仿真实验过程的截图.

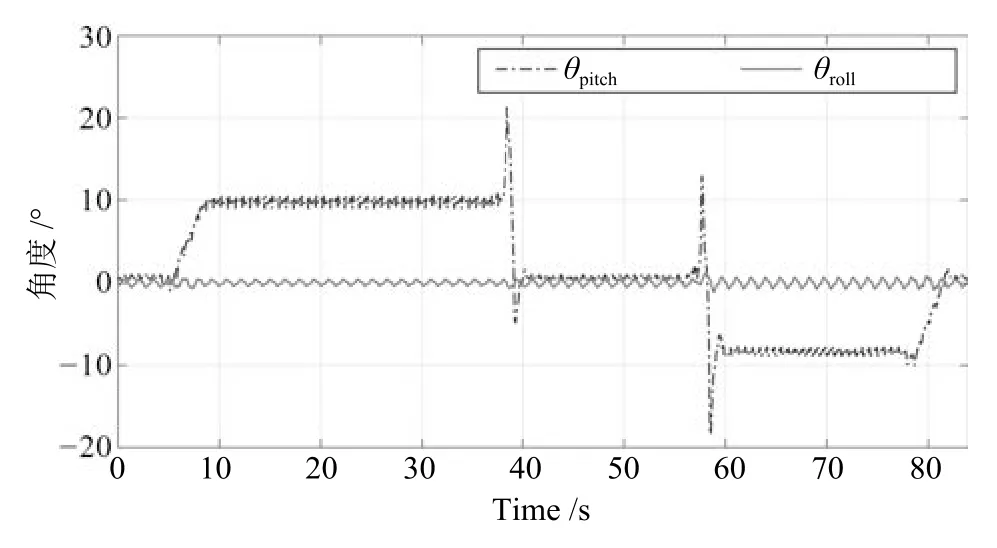
图12 身体姿态角变化Fig.12 The body attitude angle

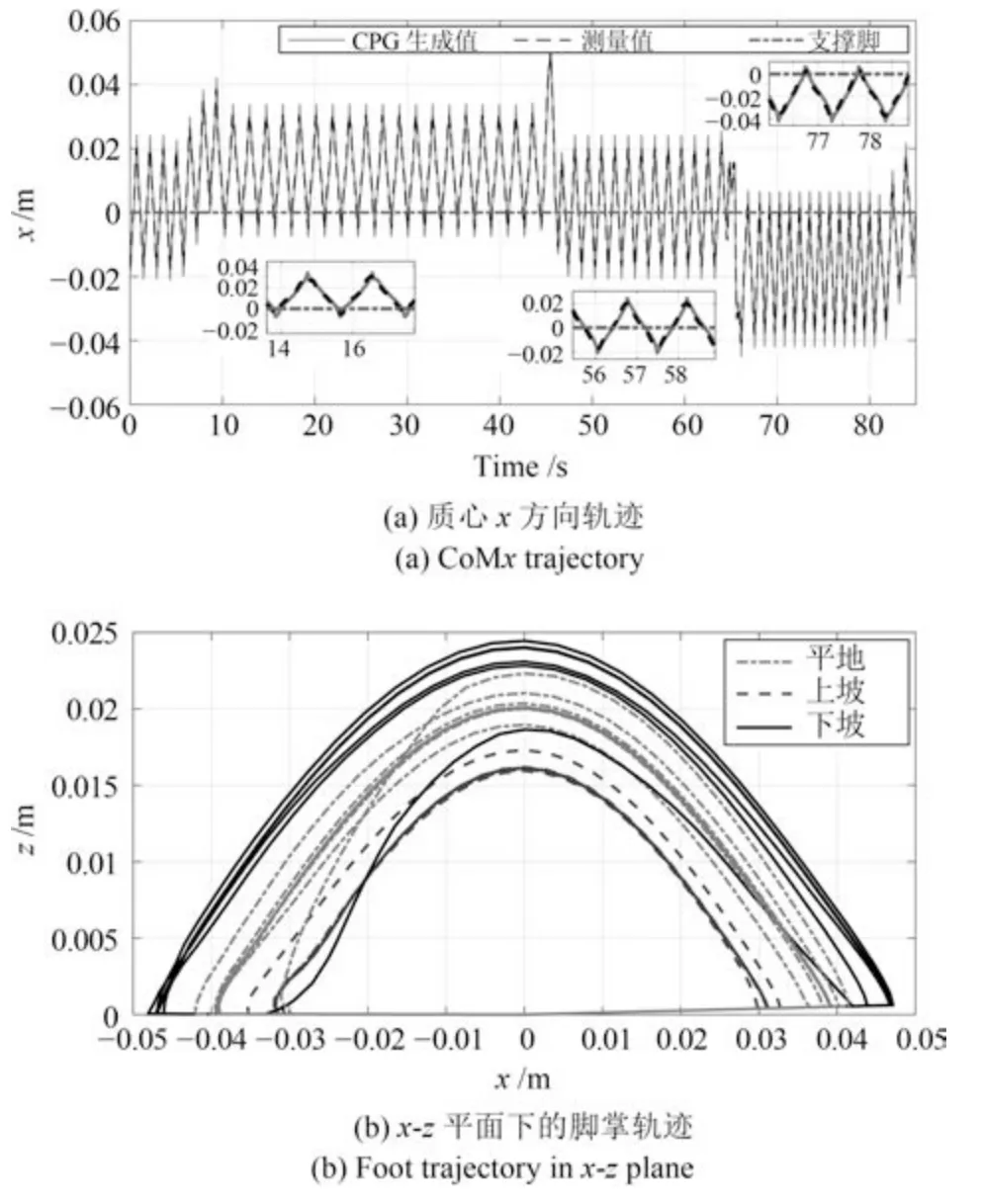
图13 自学习CPG 在线生成的质心CoMx 和脚掌轨迹Fig.13 Online generated CoMx and foot trajectory by SL-CPG

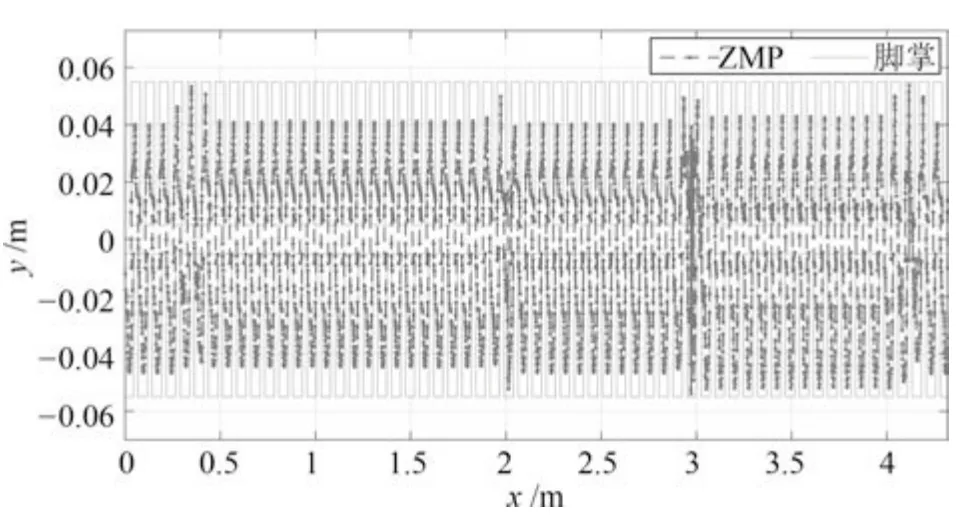
图14 ZMP 分布Fig.14 ZMP distribution

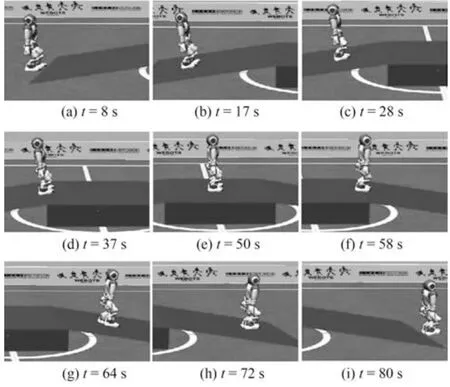
图15 坡面行走仿真截图Fig.15 Snapshots of d slope terrain adaptive walking simulation experiment

3.3.2 变坡度坡面行走仿真

本文设计的第二组实验是坡度连续增加的坡面,坡面从从左至右坡度依次是4°,6°,8°,10°和12°.自学习CPG 质心和脚掌轨迹发生器能根据坡面变化在线生成具有适应性的轨迹.图16 表示在坡度逐渐增加的坡面上身体姿态角的变化,图17 是整个实验过程的截图.

图16 身体姿态角变化Fig.16 The body attitude angle

图17 变坡度坡面仿真实验截图Fig.17 Snapshots of walking on varying slope

3.3.3 与关节空间法对比分析

基于关节空间法,在机器人行走时,每一个自由度都需要一个CPG 单元来控制,需要10 个CPG单元进行学习,其结构如图18所示.

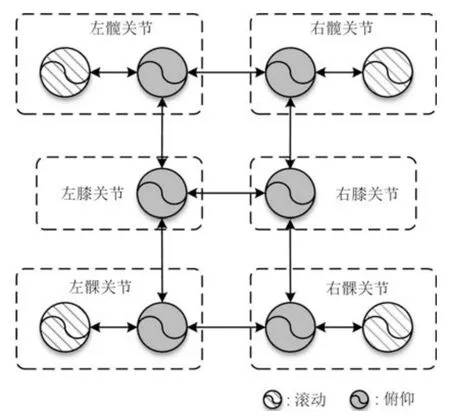
图18 CPG 网络结构图Fig.18 Network structure of CPG

CPG 关节空间法成功实现了机器人平地的行走,图19 是机器人平地行走时CPG 所产生的左腿的关节控制信号.

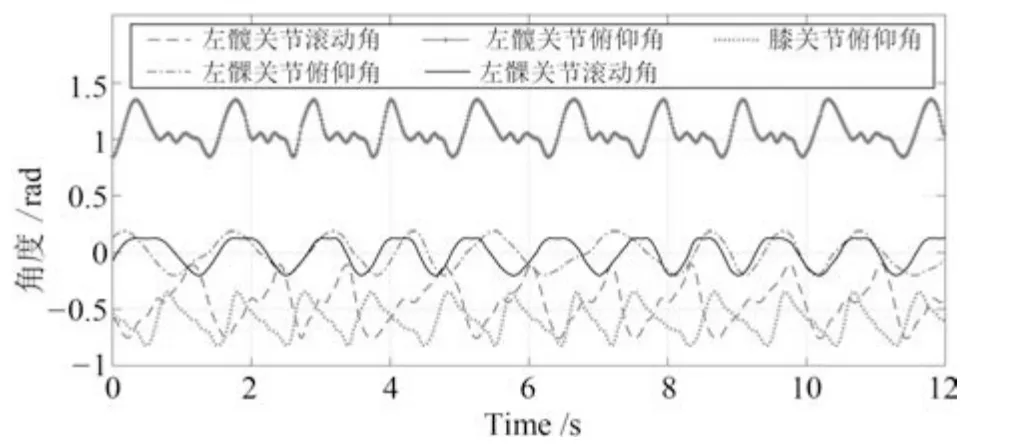
图19 左腿关节控制信号Fig.19 Control signals of left leg joints

在坡面自适应行走实验中,实验环境设置保持一致,反馈的设置和CPG 工作空间方法中相似:

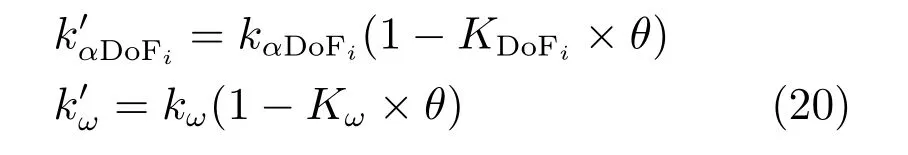
其中,kαDoFi和kω分别表示第i(i= 1,2,···,10)个自由度的SL-CPG 单元的幅值和频率调节系数,KDOFi和Kω为反馈增益系数,和为反馈调节后的更新系数.

在坡面自适应实验中,CPG 关节空间法未能成功完成实验,在NSGA-II 优化算法结束后,机器人仍然无法在坡面上实现稳定的自适应行走.在关节空间法中,机器人的质心变化是不可预测的,会导致非正常的步态产生,而且在平地行走中机器人的摇晃程度更大.相比较于关节空间法,本文所提出的工作空间法,控制网络更为简单有效,所需CPG 单元和参数较少；控制机器人的质心轨迹,有效防止机器人滑倒和倾覆,实现了机器人的自适应行走.

3.3.4 实体机器人实验

基于Webots 中的仿真结果,将程序移植到NAO 实体机器人中,测试其行走性能.由于在Webots 中没有绝对准确的动力学模型,而且仿真和实际行走时的摩擦系数不同以及实际机器人存在损耗,所以所设计的反馈回路的参数需要在相对小的范围内通过试验和误差来调制.

在本次试验中,机器人依次连续通过三个不同的地形:上坡,平地和下坡,其中上下坡的坡度均为7°左右.机器人在未知地形情况下,自学习CPG 基于机器人自身的身体姿态来自动在线调整质心和脚掌的轨迹,实现适应性行走.图20 是实验的截图,图21 是自学习CPG 在线生成的质心和脚掌轨迹;图22 是机器人行走过程中ZMP 的分布情况,其中实线代表脚掌多边形,虚线是ZMP 分布.

图20 适应性行走实验截图Fig.20 Snapshots of adaptive walking experiment

图21 自学习CPG 在线生成的质心CoMx 和脚掌轨迹Fig.21 Online generated CoMx and foot trajectory by SL-CPG

图22 ZMP 分布Fig.22 ZMP distribution

4 结束语

本文采用了4 个自学习CPG 单元分别对机器人的工作空间轨迹训练学习,得到质心和脚掌的在线轨迹发生器.自学习CPG 工作空间规划方法,可以从机器人现有轨迹或人类的行走步态中学习,并模仿人类的前庭反射,通过设计多个反馈回路来防止机器人发生打滑和倾覆.仿真和实体实验以及与传统关节空间法的对照实验,验证了所采用基于自学习CPG 的轨迹学习和生成方法以及自适应行走控制策略的有效性.本文提出的SL-CPG 模型和工作空间轨迹生成方法对足式机器人具有普适性.下一步将研究反馈控制器的设计以及基于强化学习的参数进化算法,并结合环境信息实现更为复杂地形及未知外部扰动下的自适应行走控制.