碰撞振动系统的最大Lyapunov指数计算
2021-11-13冯进钤
党 慧,冯进钤,杨 森
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
碰撞、颤碰以及伴随颤碰所产生的黏滞现象是非光滑系统动力学研究的热点问题之一。碰撞振动系统在应用数学、应用物理、工程机械等专业领域内皆有涉及。作为一种非光滑系统[1],它具有较强的非线性特征,在动力学研究中产生了较为深远的影响。碰撞振动系统通常表现为存在间隙的各活动部件之间或者活动部件与固定部件之间的反复冲击与碰撞[2]。借助于现代动力系统理论对碰撞振动系统的研究,主要集中于该系统的周期运动、分岔和混沌等[3-6]。
由于碰撞所导致向量场的不连续性,碰撞振动系统在发生高速碰撞后,在一定条件下可能还会发生颤碰现象。颤碰是碰撞振动系统中的一种新颖的动力学行为[7]。早期,BUDD等研究了线性碰撞振动系统中的颤碰及其相关动力学行为[8];ALZATE等通过实验,分析了齿轮系统中的颤碰[9]。文献[10]主要讨论了二自由度碰撞振动系统的周期黏滞运动和颤碰现象;文献[11]分析了一类二自由度含间隙弹性碰撞系统的颤碰运动特性;文献[12]研究了颤碰引起的黏滞现象,并利用Simulink进行动力学仿真。
在非线性动力学系统中,Lyapunov指数谱是判定动力系统运动的稳定性和混沌特性的一种重要工具[13-15]。目前,关于光滑动力系统的Lyapunov指数谱研究已较成熟:WOLF等利用实验时间序列提出了Lyapunov指数谱的通用算法,并对该算法进行了实验验证[16]。针对特殊的非光滑系统,STEFANSKI将映射同步用于估计确定性碰撞系统的最大Lyapunov指数[17];GALVANETTO根据映射法则,推导计算了几种不连续映射系统Lyapunov指数的数值结果[18]。FENG等考虑了在不同的随机噪声激励下时,碰撞振动系统的随机响应现象[19]。近几年,LI等研究了混合动态系统的Lyapunov稳定性切换[20];张艳龙等给出了随机干扰强度下的二自由度碰撞振动系统的Lyapunov指数的计算推导[21];李得洋等结合系统分岔图、相图和Lyapunov指数谱, 分析了系统周期运动的稳定性与各种分岔行为[22-23]。
上述Lyapunov指数的计算方法都未考虑碰撞振动系统中的颤碰以及黏滞现象,本文研究具有颤碰或黏滞现象的最大Lyapunov指数的计算,并通过算例说明计算方法的正确性。
1 碰撞振动系统的运动状态
考虑一般二维碰撞振动系统

(1)
对应的碰撞映射为
x+=R(x-),H(x)=0
(2)
式中:x∈D⊂R2,t∈R+;f为系统无约束时的向量场函数;R为碰撞映射;H(x)表示系统的运动轨线与约束面Σ之间的距离。式中下标-、+分别表示系统碰撞前后的时刻。
为了描述方便,引入碰撞面
ΣI={x∈D:H(x)=0}
(3)

(4)
(5)
当系统发生颤碰现象并从颤碰进入黏滞运动时,系统的运动过程可能存在4种运动形式,如图1所示。
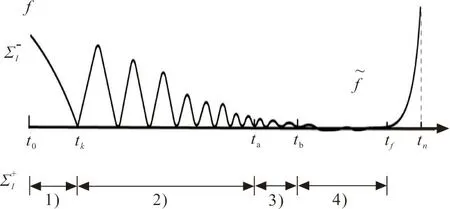
图1 运动过程示意图Fig.1 Diagram of motion process
3) 低速碰撞到颤碰:ta→tb。大量高速碰撞后,系统可能出现颤碰运动。如图1所示,系统从ta时刻进入无限次碰撞,随着振幅的逐渐减弱,最终v→0。系统运动状态由x∈Σta={x:H(x)=0,|v|<ε≪1}切换到x∈Σtb={x:H(x)=0,v=0}。为方便计算,引入彗尾映射PC,满足
xb=PCxa
(6)


(7)
式中:W(x)=(0,-(r+1))T,
如图1所示,当t∈[ta,tb]时系统进行颤碰运动,在tb时刻开始进入黏滞,当t∈[tb,tf]时系统进行黏滞运动。由于在tf时刻,加速度a=0,故系统在此时开始逃离黏滞。相应地,此时系统的运动状态由x∈Σ[tb,tf]{x:H(x)=0,v=0,a>0}切换到x∈Σ[tf,tn]{x:H(x)=0,v=0,a<0},而当t∈[tf,tn]时系统又开始作“自由”运动。
2 最大Lyapunov指数
根据上述4种情况(见图1),系统的运动状态可由连续微分方程和离散映射进行描述。易知在1)和4)情况下系统的运动由连续微分方程描述,而在2)和3)情况下系统的运动则由离散映射进行刻画。
情形Ⅰ:连续微分方程。假设系统运动方程满足
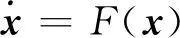
(8)
考虑对参考轨道x0(t)的一个扰动δ(x),x=x0+δ(x),并满足
(9)

Fx(x0)=(fij)2×2=fx(x0)
(10)
(ⅱ) 当x∈Σ[tb,tf]时,系统作黏滞运动,由式(7)可知
(11)
式中:
(12)
(13)
引入Khasminskii变换
(14)
将式(9)带入式(14)中化简可得
(15)
情形Ⅱ:离散映射。引入离散映射P,使系统运动状态满足
P:xn→xn+1
(16)
考虑对参考轨道x0的一个扰动δ(x),x=x0+δ(x),并满足
δ(xn+1)=DPδ(xn)
(17)

(18)
(ⅱ) 当x∈Σta时,
(19)
式中:
PC(x)=x+M1(x)+M2(x)
(20)
(21)
故
(22)
(23)
式中:f1(x)=v=Hxf(x),f2(x)=a=(Hxx+Hxfx)f(x)。
引入Khasminskii变换,将式(17)带入式(14)中,化简可得
(24)
根据动力学理论,最大Lyapunov指数可表示为
(25)
式中‖·‖皆为2范数。
系统在上述4种运动状态下的最大Lyapunov指数可划分为连续微分方程及离散映射2部分进行描述。将式(10)、式(11)分别带入式(15),式(18)、式(19)分别带入式(24),并由式(25)可知
(26)
分析式(26)可知:式中第1项为系统处于阶段1),即做无约束运动时的Lyapunov指数;第2~4项分别为系统处于阶段2)~4)时,对系统Lyapunov指数的补充项,即分别为系统处于高速碰撞、颤碰运动以及黏滞运动。
3 算 例
3.1 系统的分岔与Lyapunov指数比较
考虑谐和激励下单边碰撞振动系统,非对称结构的形状记忆合金梁模型遵循如下方程[25]:
(27)
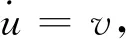
(28)
式中:r为碰撞恢复系数;h为碰撞约束位置;k为线性刚度系数;α为非线性刚度系数;μ为阻尼系数;γ为负阻尼系数;fcos(ωt)为谐和激励。


(a) u随参数f变化分岔
3.2 颤碰、黏滞运动的Lyapunov指数
为了验证系统(27)在颤碰以及黏滞情形下Lyapunov指数计算式(26)的有效性,固定系统部分参数r=0.8,k=1.0,α=1.0,μ=0.2,γ=0,ω=0.2,取初始值为(-1.5,0)T。图3给出了系统从颤碰到黏滞再到黏滞运动消失的时间历程图和最大Lyapunov指数序列图。当f=1.5时,图3(a)显示了系统作周期运动,存在颤碰和黏滞。从图3(c)中可以看到:当系统由颤碰切换到黏滞运动时,最大Lyapunov指数发生了跳跃,呈现出非光滑结构;当系统逃离黏滞,重新作“自由”运动时,最大Lyapunov指数并未发生明显跳跃,呈现出近似“光滑”结构。当f=0.81时,由图3(b)可见,系统运动过程为非周期的,图3(d)中系统的最大Lyapunov指数仅发生一次跳跃,发生跳跃的时刻与图3(b)中黏滞开始时刻同样保持一致。

(a) 时间历程(f=1.5)
图4给出了系统的相图和与其对应的最大Lyapunov指数收敛序列图。

(a) 相图(f=1.5)

4 结 语
利用不连续映射和彗尾映射对系统碰撞和颤碰的运动特性进行了有效近似,提出了系统在连续微分方程以及离散映射下的最大Lyapunov指数的计算方法。以形状记忆合金梁模型为例,讨论了系统的最大Lyapunov指数。同时,数值结果与构造的最大Lyapunov指数计算结果保持一致,验证了该计算的有效性。研究表明:碰撞振动系统在一定条件下会发生颤碰现象,并随之发生黏滞运动;最大Lyapunov指数可以有效捕捉系统的分岔、周期窗口和颤碰的切换。
