应用卡尔曼滤波的有源头靠噪声控制策略

王磊, 陈克安, 胥健, 齐旺

(西北工业大学 航海学院, 陕西 西安 710072)

区别于传统的无源噪声控制,有源噪声控制(active noise control,ANC)利用声波的相消性干涉,主要在低频范围发挥作用[1]。一般情况下,人们采用局部空间降噪代替全局降噪以降低系统复杂度,这样只需要在人耳附近获得降噪效果即可,因此有源头靠技术有着重要的实际价值[2]。

为了能够在人耳附近形成静区又不影响人的活动,误差传声器通常会放置在离人头较远的位置。为了在人耳处形成静区,主要的办法就是采用虚拟误差传感技术[3-6],这样就可以在以虚拟误差传声器为中心的较小空间内形成降噪区域。利用远程传声器技术(remote microphone technique,RMT),事先测量初级声场中物理误差传声器与虚拟误差传声器间的传递函数,以物理误差传声器处的声场估计虚拟误差传声器处的声场,从而实现虚拟误差点的有源噪声控制[7]。Kestell在自由场中利用前向差分预测外推多项式估计虚拟误差点的声压[8]。Diaz在火车车厢模型的ANC系统中使用虚拟误差传感使得人耳附近达到15 dBA的降噪量[9]。Petersen等利用卡尔曼滤波(Kalman filter,KF)准确估计出虚拟误差点的声压,从而在较宽的范围内达到降噪效果[10]。虽然以上文献采取的误差传感策略不尽相同,但是它们在ANC控制过程中均采用FxLMS算法,在收敛速度和稳态误差等方面存在限制。

KF是基于状态空间的算法。Lopes在单通道ANC系统中采用KF算法,比FxLMS和FxRLS算法获得更多的降噪量[11],在此基础上,将ANC系统的状态空间描述为简单的随机游走模型,获得了更加稳定的KF求解方法[12]。Ophem等将KF算法的应用扩展到多通道ANC系统,对参考信号进行平移,采用快速阵列算法降低了运算量[13]。Liebich等基于滤波器系数推导了新的状态转移矩阵代替简单的随机游走模型,进一步提升了收敛速度[14]。总的来说,KF算法以增加运算量为代价,提升了ANC系统的降噪性能,但其在算法稳定性上仍然存在一些问题。

本文针对虚拟误差点的噪声控制问题,采用KF算法提升系统的收敛速度和稳态误差。首先算法状态变量只包含控制滤波器系数,从根本上降低了KF的运算负担。为了进一步降低算法的运算量,采用快速阵列算法。KF中的参数对算法性能有着决定性的影响,进一步对算法进行改进,给出了过程噪声协方差矩阵Q1和测量噪声协方差矩阵Q2的估计方法,保证了滤波结果的收敛。最后与FxLMS算法进行比较,通过仿真验证提出算法的有效性及稳定性。

1 基于RMT的ANC系统

如图1所示的有源降噪头靠通常包含次级声源、物理误差传声器和虚拟误差传声器。物理误差传声器布置在距离人头较远的位置,虚拟误差传声器布置在人耳位置。实际的自适应有源控制过程包括预辨识阶段和控制阶段。在预辨识阶段估计初级声场中物理误差传声器与虚拟误差传声器间的传递函数和次级通路传递函数。虚拟误差传声器只在预辨识阶段放置,控制阶段通过物理误差传声器的声压估计该处的声压。

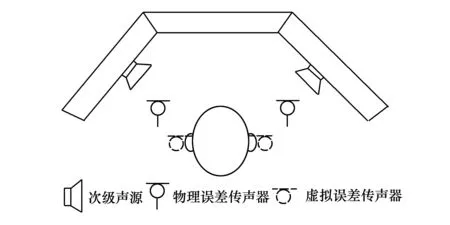
图1 有源头靠示意图

通过虚拟误差传感技术将局部静区从物理误差传声器位置处移至虚拟误差点位置。为了实现静区的传递,采用RMT的ANC系统如图2所示。

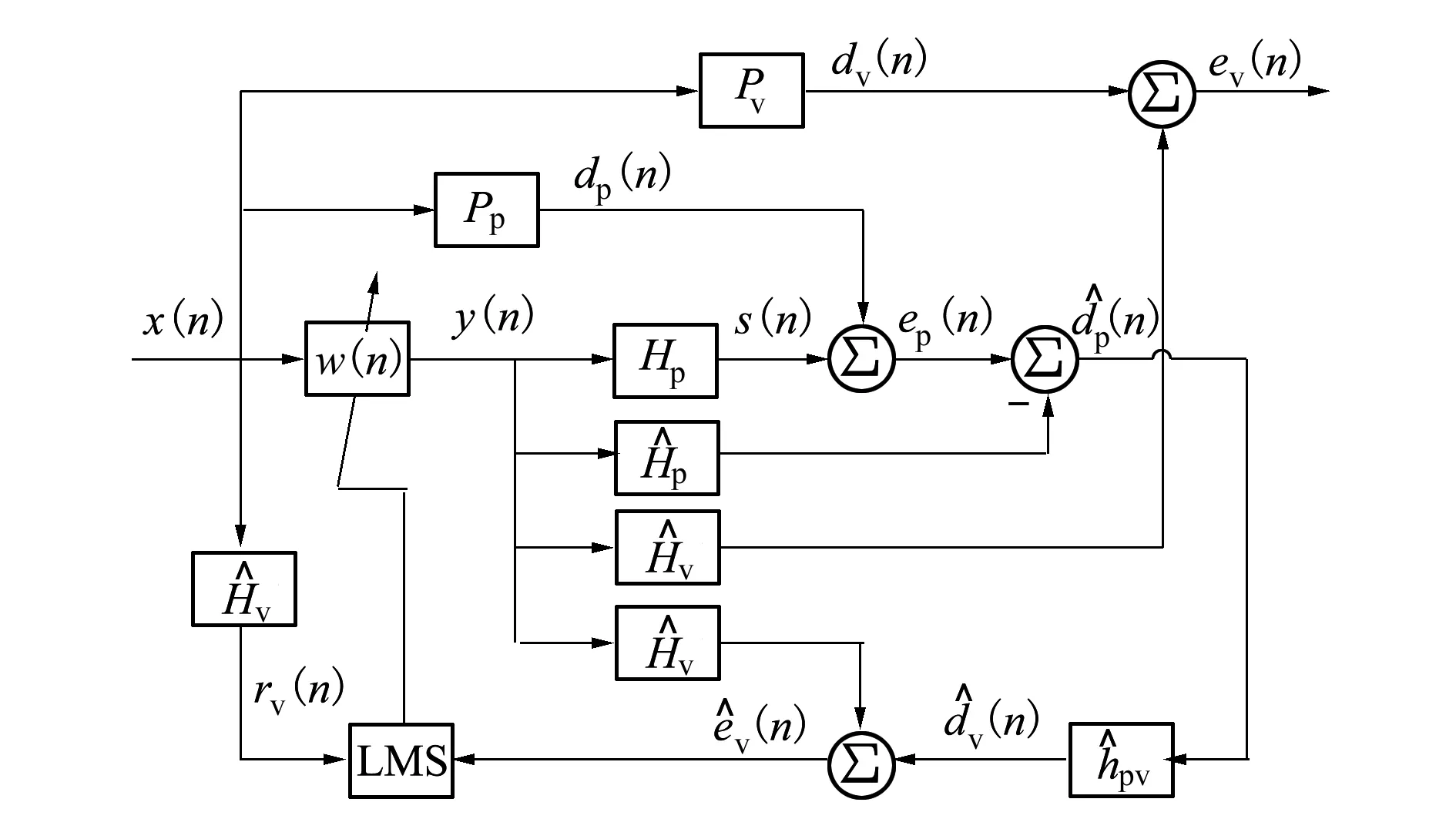
图2 基于RMT的ANC系统

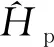
物理误差传声器处的实际误差信号ep(n)为初级信号dp(n)与次级声源在误差点形成的抵消信号s(n)的叠加

ep(n)=dp(n)+s(n)

(1)

则其初级信号的估计为

(2)

式中,y(n)为控制滤波器输出的次级信号

y(n)=x(n)*w(n)

(3)

进而可以获得虚拟误差点处的误差信号估计

(4)

通过LMS算法原理,利用滤波-x信号与估计的误差信号对控制滤波器权系数w(n)进行更新,有

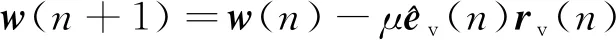
(5)

式中:μ为步长参数;rv(n)为参考信号x(n)经过次级通路滤波之后的滤波-x信号

(6)

由于迭代过程中使用的误差信号为虚拟误差点位置处的误差信号估计，则控制系统将在虚拟误差点取得降噪效果，系统性能将会受到估计准确性的影响。

2 基于KF的有源控制算法

2.1 算法描述

LMS算法对特征值扩散度具有较高的敏感性,可能导致较慢的收敛速度[15]。由于具有良好的过程参数估计,KF在收敛速度和鲁棒性方面往往优于大多数自适应算法,KF算法引入了系统的状态空间模型和状态变量等概念。基于KF的有源头靠虚拟误差点噪声控制系统如图3所示。

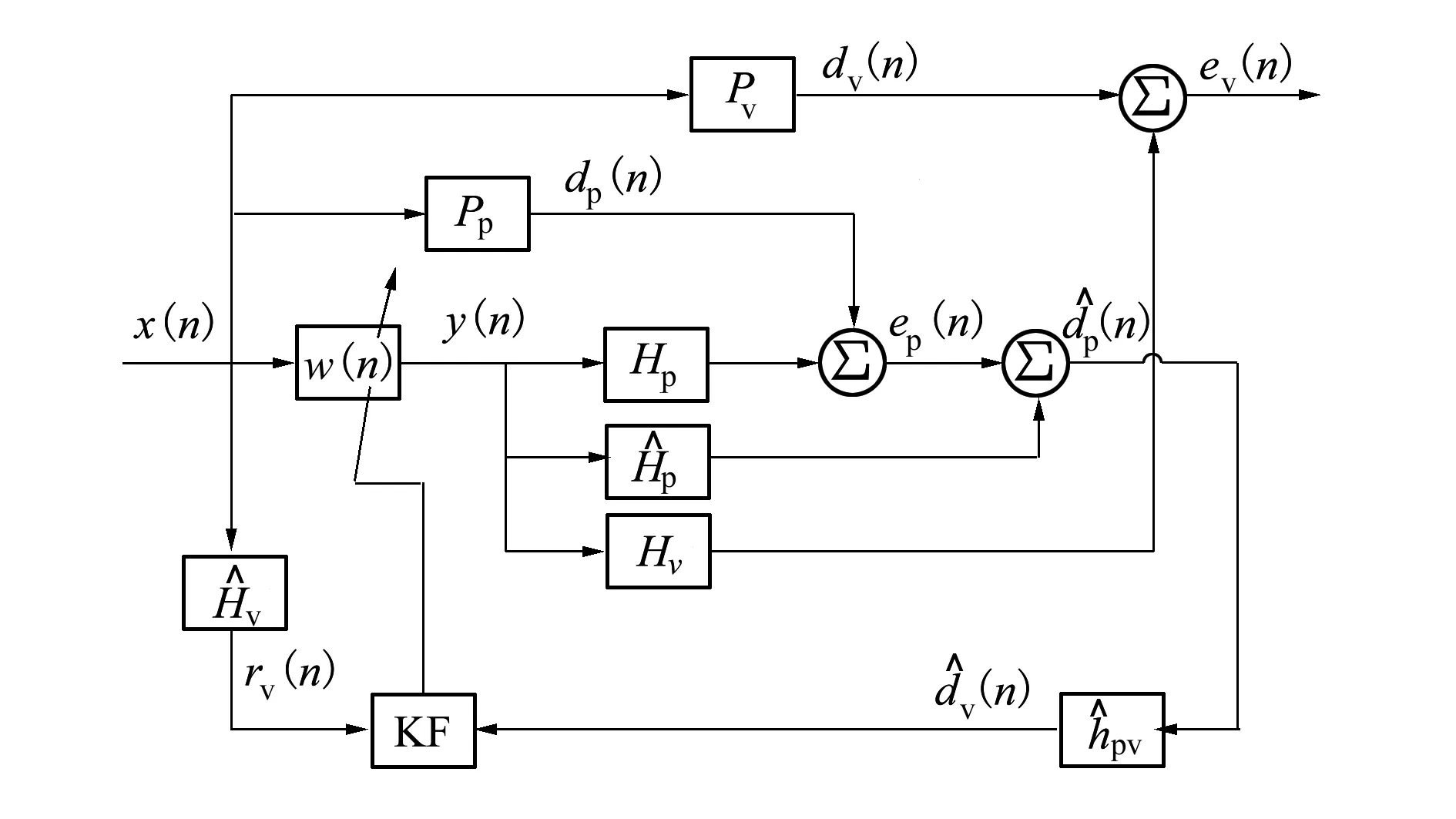
图3 基于KF的虚拟误差点ANC系统

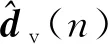
(7)

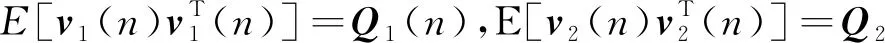
式中：I为参考传声器个数；J为次级声源个数；L为控制滤波器阶数；Kv为虚拟误差点个数。

则应用于虚拟误差点噪声控制的多通道KF算法可以如下表示

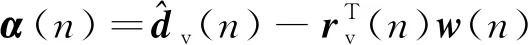
(10)

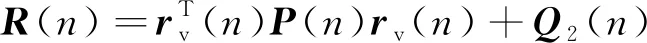
(11)

Kk(n)=F(n)P(n)rv(n)

(12)

P(n+1)=F(n)P(n)FT(n)-

(13)

w(n+1)=F(n)w(n)+Kk(n)R-1(n)α(n)

(14)

式中，P(n)为状态估计误差的相关矩阵。即

P(n)=E[w0(n)-w(n)][w0(n)-w(n)]T

(15)

表1中总结了描述有源头靠噪声控制的KF算法中用到的变量。

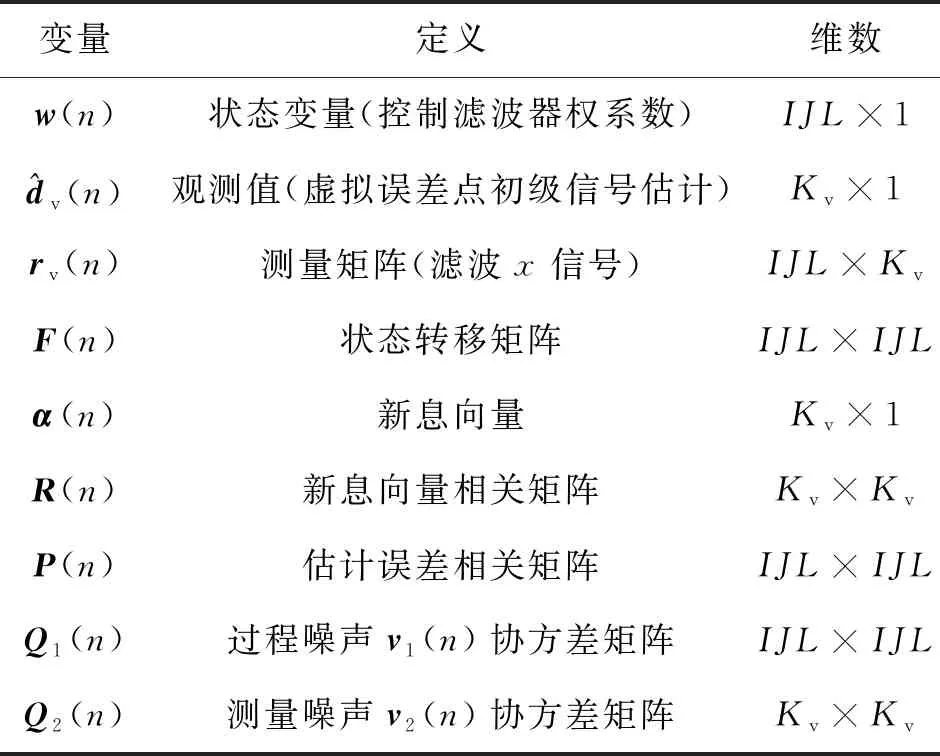
表1 卡尔曼变量小结

假设系统为随机游走模型,状态转移矩阵选为单位矩阵,即F(n)=IIJL。KF算法以增加运算量为代价,提高了系统的收敛速度和降噪效果。以单位采样时间内算法所需的乘法运算次数作为运算量,基于KF的有源头靠降噪系统的运算量为

(16)

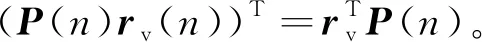
2.2 状态噪声估计

在上述模型中,已经假设整个ANC系统是线性的,且过程噪声与测量噪声皆为白噪声。参数Q1(n)表示过程噪声协方差,描述系统模型的不确定性,Q2(n)表示测量噪声协方差,描述测量的不确定性。在实际情况中,Q1(n)和Q2(n)都是不能直接观测的。针对建模不精确的问题,为了保证算法收敛,利用可观测数据对过程噪声和测量噪声进行实时估计调整。

Q1(n)可以表示为

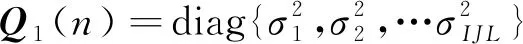
(17)

有

(18)

由(14)式可得

(19)

以时间平均代替集平均

(20)

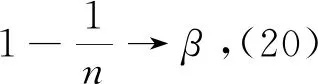
(21)

式中，0≪β≤1。

测量噪声协方差为

Q2(n)=diag{E[α(n)αT(n)]}

(22)

同样地,有

Q2(n)=βQ2(n-1)+(1-β)diag{α(n)αT(n)}

(23)

(21)式和(23)式给出了过程噪声与测量噪声协方差矩阵的实时更新策略,当参数选取不当时,利用该策略可以在一定程度上避免滤波发散。

2.3 快速阵列算法

为了降低算法的运算量,采用快速阵列算法,利用Chandrasekhar递归代替Riccati方程[16]。此时控制滤波器权系数改写为

(24)

状态估计误差的相关矩阵

(25)

该系统的状态空间方程为

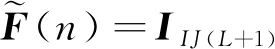
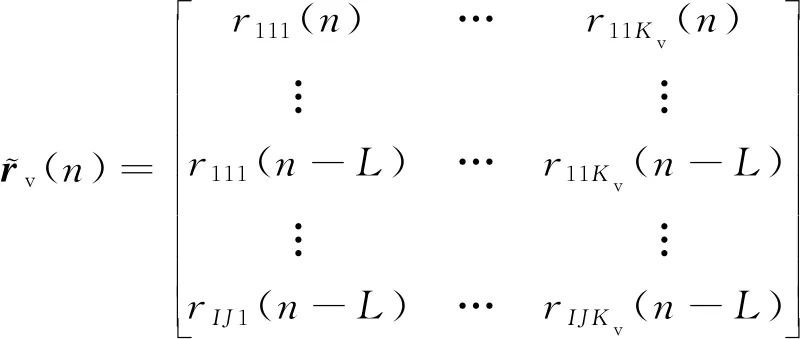
(27)

则有

(28)

式中

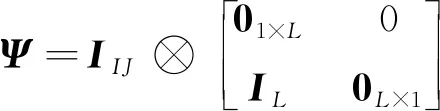
(29)

Δ=

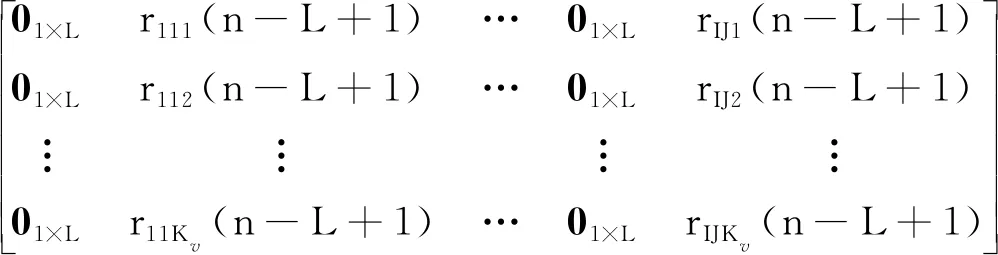
(30)

(11)～(13)式可以改写为

L(n-1)M(n-1)LT(n-1)

(34)

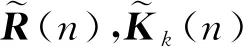
(35)

通过(35)式在后阵列中形成零矩阵块,其中Θ为酉矩阵,满足

Θ(n-1)J(n-1)ΘT(n-1)=J(n-1)

(36)

式中

J(n-1)=IK⨁M(n-1)

(37)

由(25)式可得

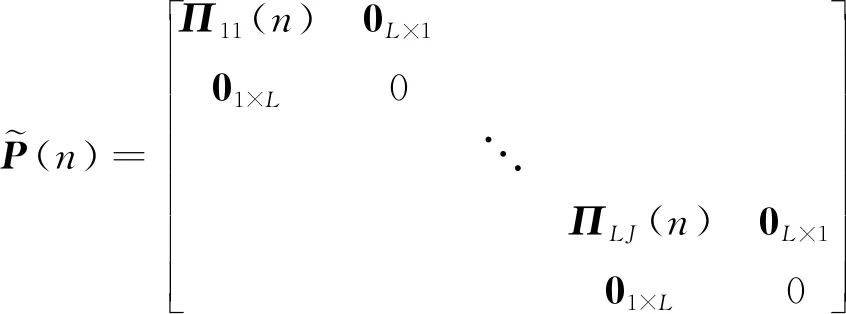
(38)

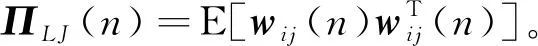
(39)

同理可得

(40)

则控制滤波器权系数的迭代为

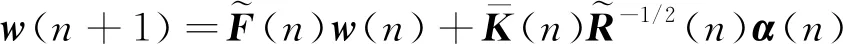
(41)

式中

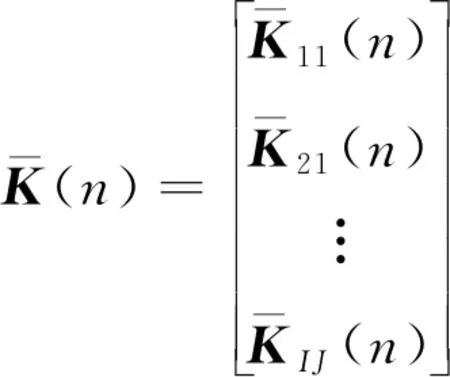
(42)

(10)、(35)和(41)式构成了多通道KF快速阵列算法,其运算量为

(43)

由(16)式和(43)式可以看出,KF快速阵列算法的运算量远远小于KF算法的运算量。如果ANC系统中I=1,J=Kp=Kv=2,M=N=128,L=256,则基于KF的有源头靠系统运算量为10 567 68次乘法,而快速阵列算法的运算量为24 720次乘法。

3 仿真与讨论

为了验证所提算法的性能,在初级噪声为宽带噪声的情况下,将提出的算法与基于FxLMS算法的有源头靠系统进行了比较。仿真数据来自普通房间中的实测有源头靠数据。系统中所含电声器件个数为I=1,J=Kp=Kv=2。初级声源位于人工头后方,虚拟误差传声器位于人工头耳内部,次级声源、物理误差传声器和虚拟误差传声器位于同一高度处。采样频率为fs=2 000 Hz。

3.1 系统预辨识

在ANC开始工作之前,首先对初级声场中物理误差传声器与虚拟误差传声器之间的传递函数及次级通路脉冲响应进行辨识,建模滤波器皆为FIR滤波器,阶数M=N=256。首先由初级声源发声,物理传声器与虚拟传声器接收声压信号,从而获得它们之间的传递函数,建模结果如图4所示。从图中可以看出,利用物理误差传声器处的初级信号可以大致估计出虚拟误差传声器处的初级信号。

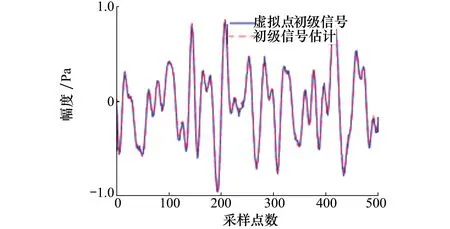
图4 虚拟误差点初级信号估计

然后由次级声源发声,获得次级通路模型。图5给出了次级声源J1分别到虚拟误差传声器Kp1和虚拟误差传声器Kv1之间的脉冲响应。由图中可以看出,次级声源到虚拟误差传声器的时延大于到物理误差传声器的时延。

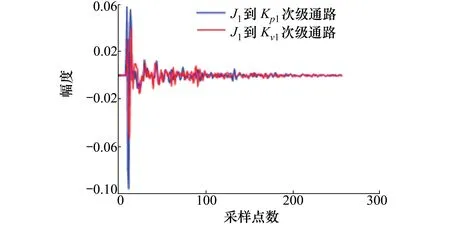
图5 次级通路脉冲响应

3.2 降噪性能对比

ANC系统中通常使用传声器作为参考传感器。在计算机仿真中,假设不存在声反馈。分别利用FxLMS算法和KF算法对估计出来的虚拟误差进行控制。控制滤波器阶数选为L=512。为了评估不同算法的降噪性能,定义

(44)

在第一组仿真中,参考信号设为零均值的高斯白噪声。将KF算法标为KF1,KF快速阵列算法标为KF2。通过试错选择算法的最佳参数,以获得每种算法的最佳性能。FxLMS算法步长参数为μ=5.23×10-4;KF1中Q1=0,Q2=10-3I;KF2中Q1=0,Q2=3×10-3I,仿真结果如图6所示。

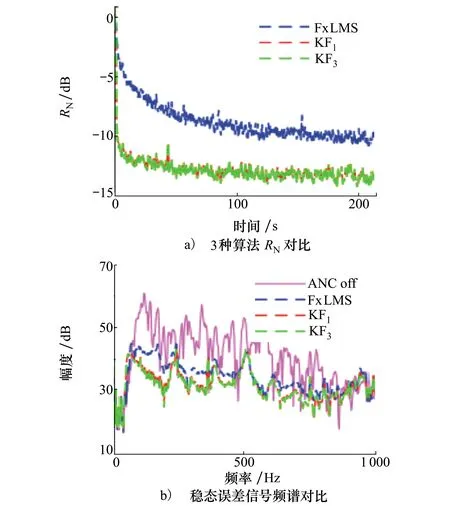
图6 算法性能比较

图6a)中给出了3种算法RN的对比,由图6a)中可以看出,在算法开始阶段,2种KF算法迅速收敛到较小的RN值。KF1算法和KF2算法能够获得近似的降噪效果。算法运行经过200 s后,FxLMS算法的RN值为-9.7 dB,KF1和KF2算法的RN值为-13.4 dB。第一个虚拟误差点处的稳态误差信号频谱如图6b)所示。3种算法的最终降噪效果近似,RN值分别为-11.3 dB,-14.1 dB和-14.2 dB。

为了使得KF算法有效,需要合理选择算法中的协方差参数Q1和Q2,如果参数选择不当,将无法达到好的降噪效果,甚至有可能引起滤波过程发散,这时,状态噪声估计的优势得以显示出来。随机选择2组Q1和Q2,KF3表示在KF1中进行状态噪声协方差估计。性能比较如图7所示,图7a)表现了全局对比,图7b)细化了0.5 s以内的局部对比。由图中可以看出,当Q1=Q2=10-6I,KF1在算法开始阶段迅速发散,而KF3依旧能达到好的降噪效果,当Q1=10-8I,Q2=10-1I,KF1和KF3都能达到收敛,但是KF3有更快的收敛速度。由此可以看出噪声估计策略可以在一定程度上保证算法快速收敛。

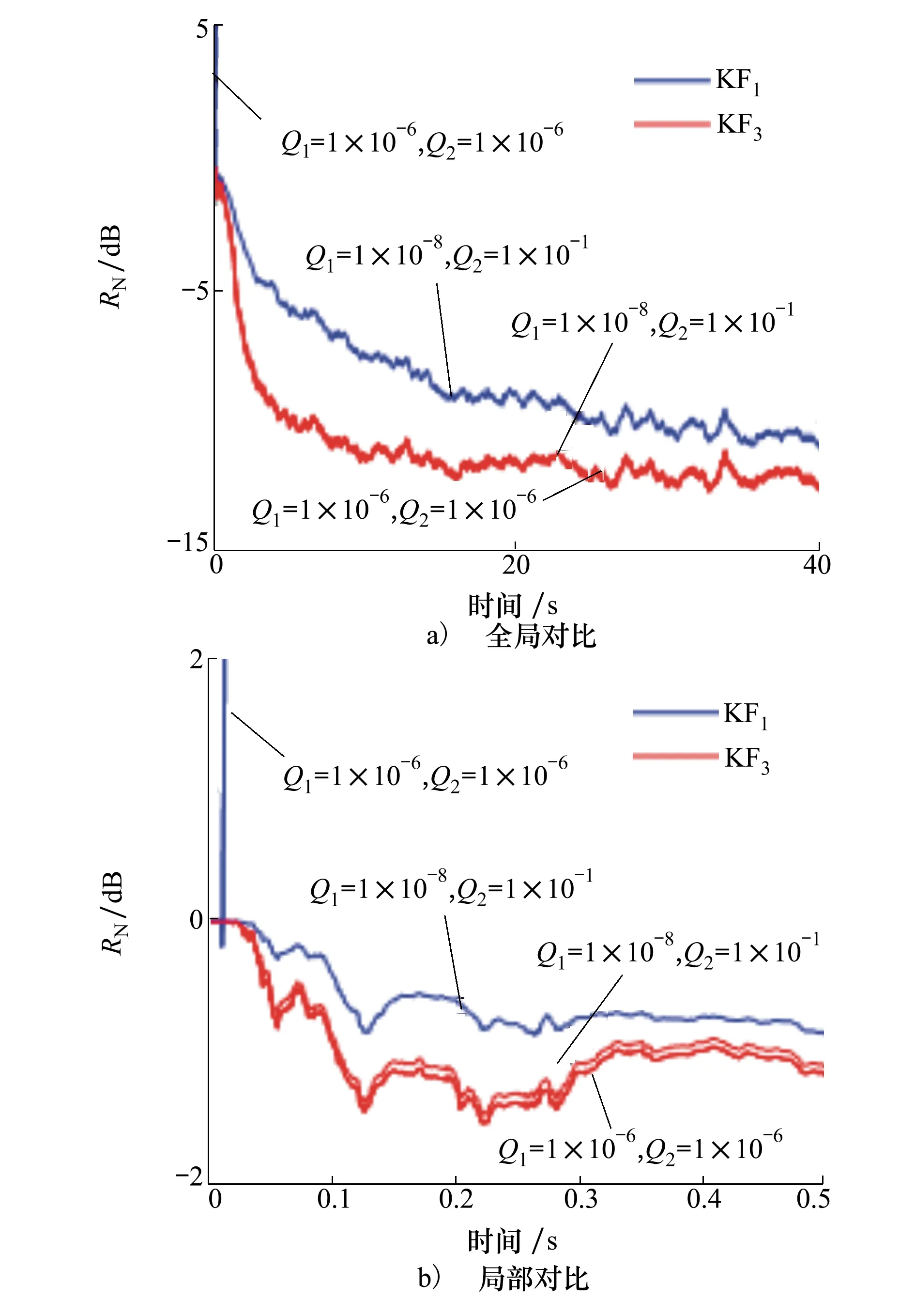
图7 状态噪声估计性能对比

在第二组仿真中,设置106 s时初级信号d(n)幅度突然发生变化,变为原来的1/2。分别对KF1和KF3算法进行仿真,结果如图8所示。图8a)给出了算法的RN对比,第一个虚拟误差点处的误差信号时域图如8b)所示。由图中可以看出,当初级信号发生突变时,KF1算法收敛缓慢,KF3算法中误差信号幅度迅速减小,收敛到较低的RN值。算法运行至200 s时, KF1和KF3算法的RN值分别为-5.1 dB和-14.2 dB。仿真结果表明,KF3算法能够有效跟踪系统的动态变化。

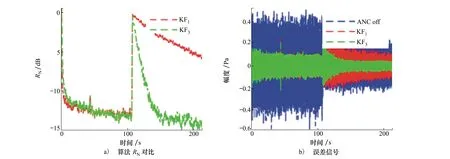
图8 状态噪声估计性能对比

4 结 论

本文对有源头靠中虚拟误差点的有源降噪进行了研究,提出了基于KF的算法,建立了状态空间方程。与FxLMS算法相比,基于KF的算法收敛速度更快,且收敛后的残余噪声更小。进一步地,为了保证算法收敛,提出了状态空间噪声协方差估计策略,在KF参数选择不当时仍然能够保证降噪效果,并且能够跟踪系统变化。引入快速阵列方法后降低了KF算法的运算量。仿真结果证明,提出的算法能够获得更好的性能。