自由漂浮空间机器人无逆运动学基于采样的运动规划
2021-11-13张红文朱战霞袁建平
张红文, 朱战霞, 袁建平
(1.西北工业大学 航天学院, 陕西 西安 710072; 2.航天飞行动力学技术国家级重点实验室, 陕西 西安 710072)
FFSR具备节省燃料,延长系统寿命等优点,被广泛用于在轨服务。FFSR构型参数中,关节角和基座姿态间存在一阶导关系,需直接考虑微分约束进行运动规划。
FFSR运动规划方法中,研究较多的包含3类。早期学者研究了系统的操控(steer)问题,即在不考虑障碍物的情况下,生成一系列的动作,让FFSR从初始构型运动到目标构型。如Vafa等基于“虚拟机械臂(virtual manipulator,VM)”[1]的模型,发展了自校正运动法[1]及“扰动图法(disturbance map,DM)”[2]。Nakamura 和Mukherjee[3]基于李雅普诺夫函数设计了双向方法。Fernandes等[4]研究了耦合刚体的运动规划方法,此类方法着眼于利用关节运动操控基座姿态;但未考虑碰撞,不能形成完整的运动规划。第二类方法是基于多项式参数化的方法,即以FFSR的初始关节角和最终关节角为端点,利用带未知系数的多项式对关节轨迹进行参数化,并以最终时刻基座姿态扰动为适应度函数,将规划问题转换为优化问题;利用遗传算法[5]、粒子群算法[6]、微分进化算法[7]等解优化问题,可得最终轨迹。该类方法不易控制轨迹的形状,因此很难考虑碰撞问题;此外,由于适应度函数计算需进行积分,因此效率低下。第三类方法是通过直接法或间接法将运动规划问题转换为非线性优化问题[8-9]。Misra等[10]于2017年基于非线性优化研究了空间机器人考虑任务约束的运动规划问题,并将问题构造为一个凸二次规划问题。该类方法求解效率高,但也存在局部最优问题。
基于采样的运动规划方法,能高效解决有高自由度构型空间的机器人运动规划问题。其中RRT(rapidly-exploring random tree)对有微分约束运动规划有很强的适用性[11]。一般情况下,运动规划多采用“先求逆运动学,再规划路径/轨迹”的框架;但这一框架存在逆运动学所求目标构型与初始构型未必在同一连通域内的隐患。针对这一问题,Bertram、Weghe等[12-13]基于有目标偏置的RRT(RRT with Goal Bias,GB-RRT)给出了解决方案,即不求逆运动学,而是直接引入目标末端位姿导引生长。在该方案中,用于目标末端位姿导引生长的局部规划含一个迭代过程,每次迭代通过雅克比矩阵的转置,将末端位姿误差映射到构型空间,从而产生一系列越来越接近目标末端位姿的构型,但该方案针对固定基座机械臂的路径规划问题,而FFSR的运动规划需直接考虑微分约束。此外,固定基座机械臂执行机构自由度大于末端位姿自由度,但FFSR末端末端位姿导引生长,除要求具备最终收敛到目标末端位姿的能力外,还需保证基座姿态扰动不能过大,因此执行机构自由度不足。
本文以GB-RRT为框架设计规划算法,解决FFSR从初始构型到目标末端位姿的运动规划问题。为适应FFSR直接考虑微分约束的需求,在Weghe等[13]提出的方法基础上,在每次迭代中引入积分机制;为克服FFSR执行机构自由度不足的问题,提出适时调节基座姿态的目标末端位姿导引生长局部规划器,以调节末端位姿为主,同时在必要时兼顾考虑基座姿态的调节。
1 自由漂浮空间机器人的运动学方程
FFSR如图1所示,符号定义与文献[14]相同。

图1 FFSR模型简图
1.1 仅考虑几何关系的运动学方程
1.1.1 姿态方程
IRe=feR(q)
(1)
FFSR的EE姿态角Ψe与IRe对应,因此
Ψe=feΨ(q)
(2)
1.1.2 位置方程
FFSR末端执行器位置pe为

(3)
1.1.3 速度方程
FFSR末端执行器角速度ωe为

(4)
末端执行器线速度ve度为

(5)

(6)
Jb,Jm的表达式见文献[14]。
1.2 动量守恒方程
FFSR的动量方程为
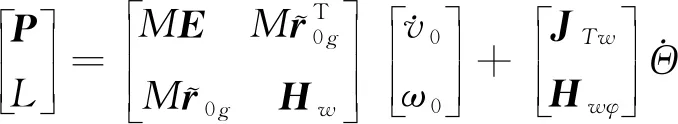
(7)
式中,P与L分别为FFSR的线动量、角动量,相关矩阵的定义间文献[14]。令
1.3 考虑动量守恒后的运动学方程
1.3.1 基座姿态角一阶导方程


(8)
取上述方程后3行,可得基座角速度ωb为

(9)


(10)
式中
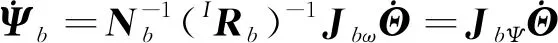
(11)
式中,JbΨ为与基座姿态角相关的雅克比矩阵。
1.3.2 状态转移方程
考虑(11)式,则FFSR的状态转移方程为
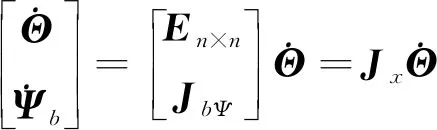
(12)
式中,Jx为与状态转移相关的雅克比矩阵。
1.3.3 广义雅克比矩阵
考虑(6)式以及(8)式,可得
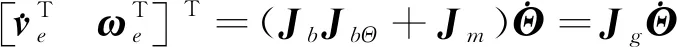
(13)
Jg为广义雅克比矩阵。
1.3.4 考虑线动量守恒积分形式后的方程
FFSR的线动量可积分为位置形式

(14)


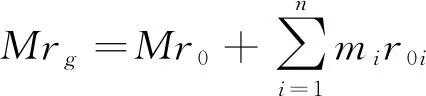
(15)
进而

(16)
给出构型参数q,可计算在惯性空间之中的表示Ibi,Iai,进而可计算r0,即q为构型参数q的函数。再考虑(3)式,可知pe为q的函数
pe=fep(q)
(17)
综合考虑(1)式以及(17)式,可得端位姿xe与q间的映射关系
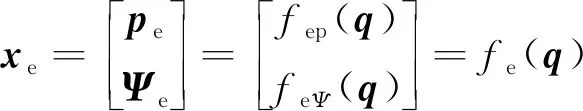
(18)
2 FFSR无逆运动学基于采样的运动规划
算法伪代码如Algorithm 1所示,在每次迭代中,利用随机采样构型qSample或目标末端位姿xed来导引树的生长,这2种生长分别称为随机导引生长(Extend-Randomly()函数)与目标末端位姿导引生长(Extend-Toward-Goal())。每次迭代生成一个随机数p∈[0,1],若p algorithm 1 GB-RRT for FFSR1tree.V.init(qI)2for i=1 to K do3 if rand() 2.2.1 随机构型导引生长局部规划器 随机构型导引生长选择离qsample最近的节点作为待扩展点qextended,并从qextended向qsample进行局部规划,以生成局部轨迹以及新的节点。 algorithm 2 extend-randomly1qsample=random-config()2qextend=nearest-node(tree,qsample)3qpresent=qextend4last-checked-q=qpresent5shall-end=false6while all(shall-end=false)7 Jb=Jacobian(qpresent)8 Jx=[Jb,eye(n,n)]9 Δq=qsample-qpresent10 JV=inv(Jx)*Δq11 BV=Jb*JV12 qpresent=qpresent+[BV;JV]*time-step13 If max(qpresent-last-checked-q)>= collision-check-thresh14 is-collision=collision-check(qpresent)15 last-checked-q=qpresent17 shall-end=check-termination()19return (19) (20) 从而得到构型速度 (21) 通过积分,更新构型 (22) 对qpresent进行碰撞检测,以保证所生成的局部轨迹处于自由构型空间。若满足下述任何一个条件,则停止迭代:①检测出碰撞;②构型超出限制,即基座姿态扰动超出限制,或者关节角度超出范围;③构型参数之中最大扩展值达到一定的阈值。 2.2.2 适时调节基座姿态的目标末端位姿导引生长局部规划器 algorithm3 extend-toward-goal1qextend=nearest-node(tree,Xgoal) 2qpresent=qextend 3last-checked-q=qpresent 4shall-end=false 5while all(shall-end=false) 6 JB=Jacobian(qpresent) 7 JG=general-Jacobian(qpresent) 8 ΔX=Xgoal-f(qpresent) 9 ΔqB=qBgoal-qBpresent 10 JV-for-EE=pinv(JG)*ΔX 11 if ΔqB>B-adjust-thresh 12 JV-for-BA=pinv(JB*null(JG))*ΔqB 13 else 14 JV-for-BA=0 15 JV=JV-for-EE+null(JG)*JV-for-BA 16 BV=Jb*JV 17 qpresent=qpresent+[BV;JV]*time-step 18 if max(qpresent-last-checked-q)>=C-check-tresh 19 is-collision=collision-check(qpresent) 20 last-checked-q=qpresent 21 shall-end=check-termination() 22return 目标末端位姿导引生长,即选择离xed最近的点作为待扩展点qextended,并从qextended向xed进行局部规划;其要求尽可能消除相对于xed的误差,同时保证Ψb不超出取值范围。本文提出适时调节基座姿态的目标末端位姿导引生长其局部规划器,其伪代码如Algorithm 3所示。作为执行机构的FFSR操作臂关节仅有7个自由度,而末端位姿任务为六自由度,基座姿态为三自由度。相对于到达xed以及保持Ψb处于一定取值范围的要求,执行机构自由度不足;因此若在局部规划的每一次迭代中,同时调节xe和Ψb,则末端位姿误差无法收敛。 (23) (24) (25) 获得动作后,后续其他步骤与2.2.1节中相应的步骤相同。本局部规划器的终止条件包含:①检测出碰撞;②构型超出限制,即基座姿态扰动超出限制,或者关节角度超出范围;③到达目标。 表1 FFSR的动力学以及几何参数 表2 FFSR的D-H参数 36次迭代后,FFSR的末端到达目标位置,规划结束。如图2a)所示,图中淡蓝色为初始构型,红色为最终构型。从初始构型到目标末端位置的运动历程如图2b)所示,整个过程中未发生碰撞。关节角、基座姿态随时间的变化分别如图3所示,从图3b)可看出,基座姿态满足取值范围限制。 图2 场景1:初始构型与最终构型,从初始图3 场景1:关节角及基座姿态变化曲线构型向目标末端位置的运动历程 116次迭代后,到达目标末端位姿,规划成功;图4a)中,红色为最终构型,青色为初始构型。从初始构型向目标末端位姿的运动历程如图4b)所示,整个过程未发生碰撞。关节角、基座姿态随时间的变化如图5所示,可发现基座姿态处于取值范围内。 图4 场景2:初始构型与最终构型,从初始图5 场景2:关节角及基座姿态变化曲线构型向目标末端位姿的运动历程 本文基于GB-RRT设计了FFSR无逆运动学的运动规划算法,并提出适时调节基座姿态的目标末端位姿导引局部规划器,引入参考目标基座姿态、基座姿态误差阈值。在该局部规划器的每一次迭代中,只有相对于参考目标基座姿态误差达到阈值,才调节基座姿态,否则只调节末端位姿。该局部规划器所生成的轨迹能满足基座姿态取值限制,且具备让末端位姿误差收敛的能力,克服了FFSR执行机构自由度不足的问题。
2.1 局部规划器设计



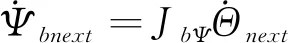
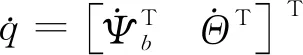






3 仿 真

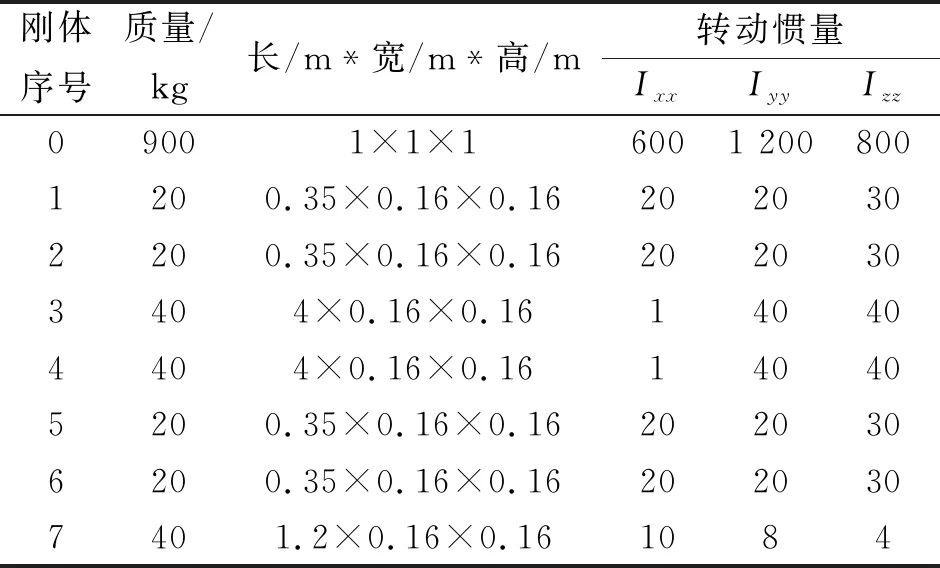
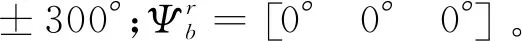

3.1 场景1的结果

3.2 场景2的结果

4 结 论
