基于MATLAB 的整体式转向梯形机构的优化设计
2021-11-13赵振全汪兆兴韩国强
赵振全,曹 智,汪兆兴,韩国强,屠 强
(1.沈阳航空航天大学 机电工程学院,辽宁 沈阳 110136;2.沈阳航达机载设备有限公司 设计所,辽宁 沈阳 110048)
汽车转向梯形机构的设计在汽车设计中占据重要的地位,转向梯形机构的结构参数直接影响汽车的转向性能,合理的设计可以保证汽车在转向时内、外转向轮尽可能作无滑动的滚动,从而减小轮胎的磨损,保证良好的转向性能并提高汽车的操纵稳定性。本文以某型地面保障设备的整体式后置转向梯形机构作为优化设计实例,通过建立转向梯形机构简化的平面数学模型,以MATLAB 软件作为主要优化工具进行优化设计,获得了理想的优化结果。
1 整体式转向梯形机构建模与特性计算
1.1 整体式转向梯形机构建模
1.1.1 基本假设
本文以整体式转向梯形机构作为研究对象,在合理的范围内,为了使所求的目标函数不过于复杂,便于设计计算,作出如下基本假设:①忽略转向梯形机构零部件之间的空间夹角和间隙;②假设车轮为刚性,忽略轮胎弹性侧偏等对转向特性的影响;③忽略车轮定位参数对转向机构运动的影响。
1.1.2 理想的转向梯形机构内侧转向轮转角函数
理想的整体式转向梯形机构的理论基础是阿克曼转向原理。阿克曼转向原理的特点是:汽车在直线行驶时,转向轮和定向轮的轴线是相互平行的,并且都与汽车纵向中心面垂直;汽车在转向行驶时,转向轮和定向轮都绕同一个瞬时中心做圆周滚动。理想的内、外侧转向轮转向角关系简图如图1 所示,图中θi表示内侧转向轮的转角,θo表示外侧转向轮转角,K 表示主销间距(两主销中心线延长线到地面交点之间的距离),L 表示设备的轴距。
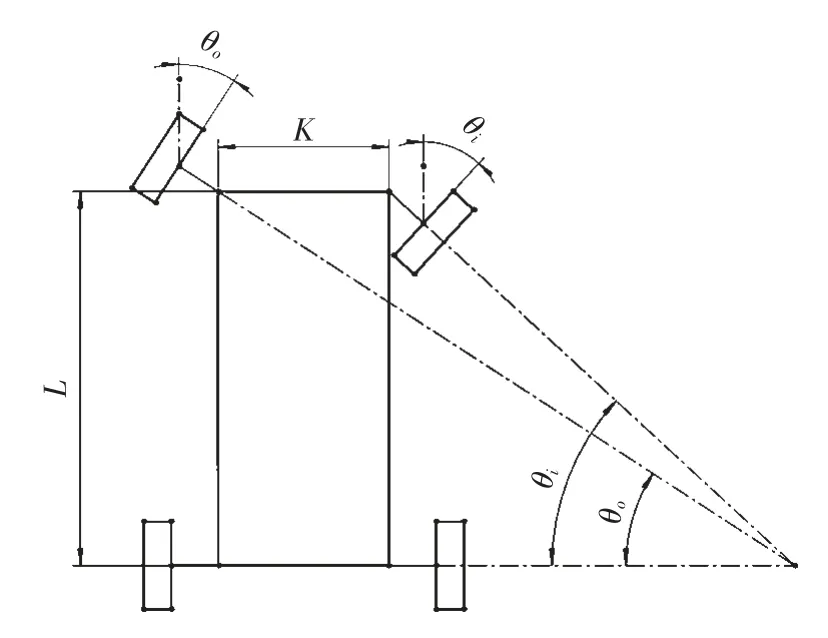
图1 理想的内、外侧转向轮转向角关系简图
若要保证所有车轮在转向时都以同一个瞬时转向中心行驶,则转向梯形机构应保证内、外侧转向轮的转向角有如下关系:

若取θo为自变量,则因变量θi的期望值为:
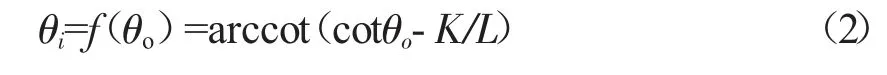
1.1.3 实际的转向梯形机构内侧转向轮转角函数
实际情况下,组成转向梯形机构的各个零部件之间存在着各种误差,转向梯形机构只能近似地满足上述理想情况下的转角函数。转向时内、外侧转向轮实际的转角关系如图2 所示。图中实线四边形ABFE 是转向前的转向梯形机构形状,虚线四边形ABF1E1是外侧转向轮转过θo以后的转向梯形机构形状。

图2 转向时内、外侧转向轮实际的转角关系
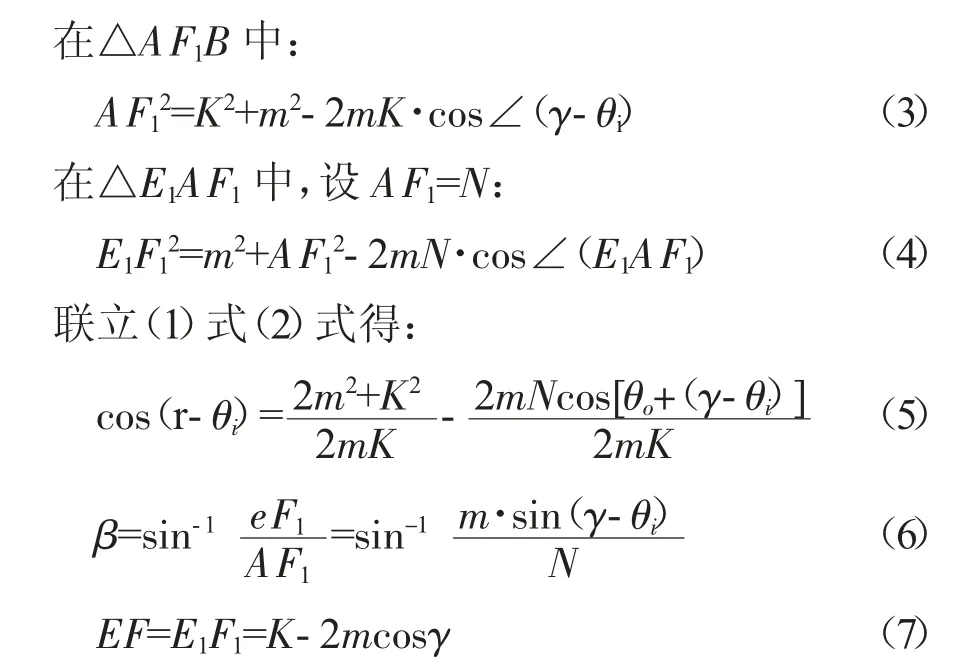
联立式(3)~(7)得内侧转向轮实际转角:
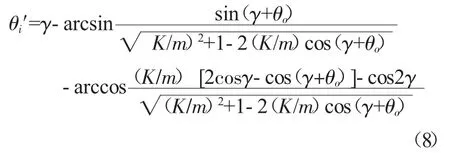
式中:m 为转向梯形机构的臂长;γ 为转向梯形机构的底角;θo表示外侧转向轮转角;表示内侧转向轮的实际转角。
1.2 转向梯形机构特性计算
为了分析整体式转向梯形机构中内侧转向轮的实际转角与理想转角之间的误差值,选取某型地面保障设备的整体式后置转向梯形机构作为实例分析:设备轴距L=1750mm ;主销间距K=1030mm;转向梯形机构的臂长m=162mm;转向梯形机构的底角γ=81°。应用MATLAB 软件对内侧转向轮的实际转角与理想转角进行对比,在MATLAB 软件上编辑的M 文件如图3 所示,得到的运行结果如图4 所示。
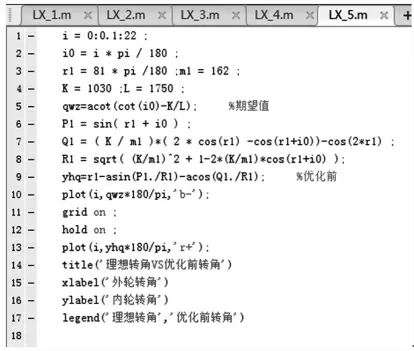
图3 输出图形程序
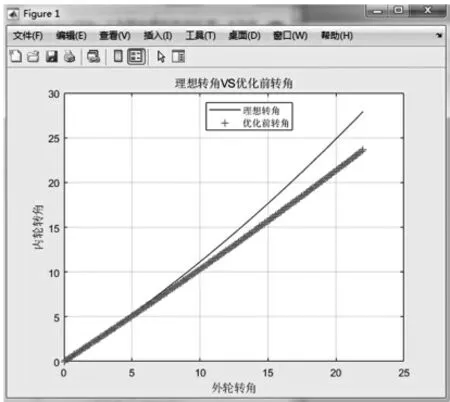
图4 化前的内侧转向轮的实际转角与理想转角
从图4 中可以看出,随着外侧转向轮转角的增大,内侧转向轮的实际转角与理想转角的偏差会逐渐增大,尤其是在外侧转向轮转角达到极限位置时,偏差也达到了最大值。而某型地面保障设备在转向时,牵引杆往往处于转向极限位置,而此时轮胎的侧滑情况最为严重,轮胎磨损严重。
2 转向梯形机构的优化设计
2.1 确定目标函数

将(2)式和(8)式代入(9)式得
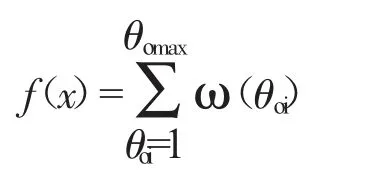

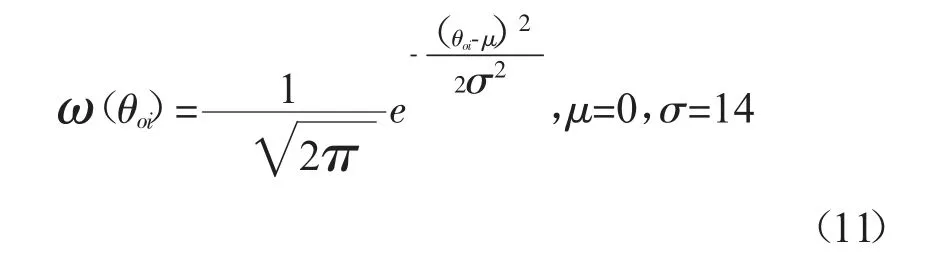
在MATLAB 软件上编辑目标函数f(x)的M 文件,内容如图5 所示。

图5 优化目标函数
2.2 确定约束条件
在转向梯形机构设计中,当设计变量转向梯形机构的臂长m 及转向梯形机构的底角γ 过小时,会造成转向横拉杆上的转向力过大;当m 过大时,会使转向梯形机构过大,影响整体布局,所以对m 的上下限设置约束条件;当γ 过大时,转向梯形机构近似于矩形,使得目标函数值越来越偏离理想值,所以对γ 的上下限设置约束条件。综上所述,设计变量的约束条件为:
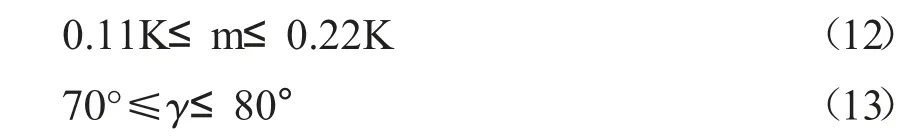
此外,由机械原理知识可知,四连杆机构的传动角δ 不宜过小,通常取δ≥δmin=40。如图2 所示,转向梯形机构在汽车右转弯到极限位置时,δ≥δmin即可。利用该图所做的辅助虚线及余弦定理,可推出最小传动角约束条件为

式中:δmin为最小传动角;δmin为设计变量m 及γ 的函数。
在MATLAB 软件上编辑目标函数f(x)的优化约束条件的M 文件,内容如图6 所示。

图6 优化约束条件
2.3 优化结果分析
运用 MATLAB 优化工具箱中的fmincon 有约束的非线性最小化函数,编辑好主程序、初始点及设计变量m 及γ 的上下限,内容如图7 所示。

图7 优化主程序
运行该M 文件,MATLAB 软件就会对该转向梯形机构进行优化分析,最后得出最优解,如图8 所示。
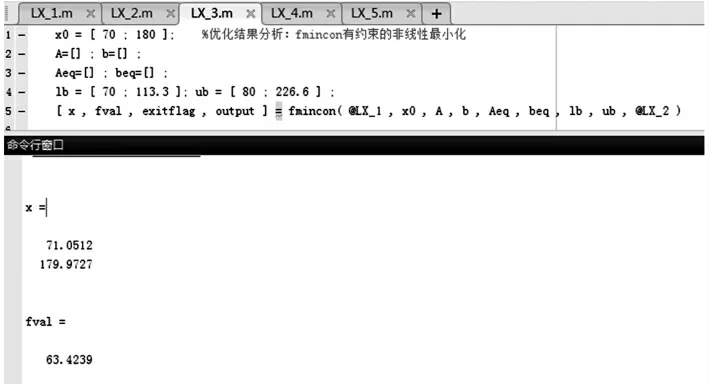
图8 优化结果
由图8 可知,优化后的转向梯形机构的梯形臂长m=179.9727mm,梯形底角γ=71.0512°。对参数取整后得梯形臂长m=180mm,梯形底角γ=71°。
应用MATLAB 软件对内侧转向轮的理想转角与优化前后转角进行对比,在MATLAB 软件上编辑的M 文件如图9 所示。根据图10 所示的运行结果,相比于优化前的曲线,优化后的曲线更加接近理想曲线,达到了优化的效果。

图9 输出图形程序
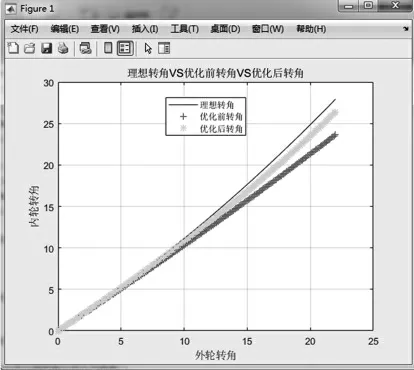
图10 内侧转向轮的理想转角与优化前后转角
3 结论
本文主要选取某型地面保障设备的整体式后置转向梯形机构作为分析对象,通过转向特性阿克曼转向原理建立了整体式转向梯形机构简化的平面数学模型,确定了转向梯形的特性函数、优化目标函数及约束条件,运用MATLAB 优化工具箱中的fmincon函数求得最优解。
利用Matlab 软件作为优化设计工具,避免了繁琐的程序设计与调试,缩短了研发周期及成本,优化结果清晰明了。此方法对新转向梯形机构的设计和旧转向梯形机构的改进都有很大的指导作用。
