高速铁路全封闭声屏障列车压力波和微气压波数值模拟研究
2021-11-13何旭辉吉晓宇敬海泉葛辉凯张甲振
何旭辉,吉晓宇,敬海泉,*,葛辉凯,张甲振
(1. 中南大学 土木工程学院,长沙 410075;2. 高速铁路建造技术国家工程实验室,长沙 410075;3. 雄安高速铁路有限公司,保定 071700;4. 河北交投物流有限公司,石家庄 050000)
0 引言
21世纪以来,随着我国高速铁路技术的不断发展,列车运行速度大幅提升,显著提高了铁路运输的效率和乘客的乘车舒适性;然而,列车高速运行时也会产生较大的振动噪声和气动噪声,给高铁沿线的居民带来一定的困扰。为了进一步提升高速铁路沿线居民的居住舒适性,在线路两侧设置声屏障是高速铁路降噪的主要措施之一。目前,应用较多的是直立式和折角式声屏障。就降噪性能而言,全封闭声屏障最为突出,近年来逐渐对其在实际工程中的应用展开研究。高速列车驶过结构相对封闭的声屏障时,会产生强烈的气动效应,使声屏障壁面受到压力波的作用,对声屏障的结构强度产生影响。因此国内外学者对列车驶过声屏障时的气动效应开展了一些研究,龙丽平[1]、陈向东[2]等采用数值模拟技术对高速列车驶过直立式声屏障时产生的气动效应进行了研究,分析了车速、声屏障高度等因素对声屏障壁面压力的影响。Xiong等[3]通过现场实测研究了列车速度、运行线路、测点位置、编组长度和环境风速对CRH380A动车组在声屏障上产生的脉动压力的影响。目前,大部分研究重点针对直立式声屏障的列车气动效应,对于全封闭声屏障列车压力波和微气压波的研究较少。由于全封闭声屏障结构类似于相同长度的隧道,既有隧道空气动力学的研究成果对全封闭声屏障气动力研究具有借鉴意义。
Triebstein[4]和Ozawa[5]对列车经过隧道时隧道壁的风压变化进行了现场实测;刘堂红等[6]通过实车测试研究了200 km/h动车组通过隧道时的压力波与微气压波特性;陈厚嫦等[7]通过现场实测,研究了350 km/h动车组在隧道内运行和交会过程中的气动效应,发现动车组通过隧道时,车外空气压力基本随列车速度和隧道长度的增加而增加;韩运动等[8]通过实车测试,得到单车通过工况的最不利隧道长度,及两车交会工况的最不利双线隧道长度、最不利交会位置、最不利编组长度等计算公式。高品贤等[9]采用浅水槽拖动模型试验模拟隧道压力波的变化过程;王学英等[10]采用风洞弹射试验方法对列车进入隧道过程中压力的变化情况进行测试得到了压力波产生和变化的一些规律;Iida等[11]、Liu等[12]通过动模型试验的方法研究了列车通过隧道时产生的压缩波与微气压波。Zhang等[13]基于动模型试验的方法研究了不同速度的列车通过隧道时,列车表面和隧道壁面上的气动荷载分布。Li等[14]通过数值模拟方法,发现列车通过隧道时,隧道内和列车表面的压力变化幅值均与列车速度的平方成正比;向新桃[15]基于CFD商业软件及其二次开发阐明了隧道表面和列车表面瞬变压力的形成机理;梅元贵等[16]采用SSTk-ω高雷诺数湍流模型研究了我国高速列车通过隧道产生的初始压缩波的基本特性,发现初始压缩波的压力时间变化率峰值与车速的三次方近似呈正比关系;Liu等[17]利用RNGk-ε湍流模型模拟了列车驶过隧道时产生的瞬态荷载,发现压力波在隧道内传播的过程中具有较好的一维特性;刘金通等[18]采用滑移网格技术得到了隧道内压力梯度的最大值及其出现位置与列车速度和隧道阻塞比之间的近似关系式。
本文借鉴隧道空气动力学的研究方法,利用数值模拟技术,采用三维非定常可压缩湍流模型,研究某高速列车通过圆形全封闭声屏障时产生的压力波和出口微气压波的时变规律,以期为以后的工程应用提供一定参考。
1 数值计算方法
1.1 数值计算模型
以我国某高速列车为研究对象,如图1所示。列车采用八列编组,总长约203 m,车体高3.7 m,宽3.38 m。为了提高计算效率,节约计算资源,在不影响计算准确度的前提下对其外形进行了简化处理,忽略受电弓、转向架、车轮和门窗等部件,简化车厢连接处,仅保留列车的典型气动外形[19]。

图1 高速列车模型Fig. 1 A high-speed train model
全封闭声屏障数值模型以我国某在建高铁线路声屏障为原型,根据结构设计初步方案,设置圆形全封闭声屏障横断面半径为6.913 m,长度为840 m,高为9.637 m,横截面面积为110.5 m2,线间距为5 m。声屏障内部每隔2 m设置H型钢框架,型号为H500*300*12*25,计算过程中将其简化成了实体结构,如图2所示。

图2 圆形全封闭声屏障模型Fig. 2 An enclosed sound barrier model
1.2 计算区域
整个计算域包括加速段、声屏障段和缓冲段三个部分;为了使列车的加速过程更加充分,不致因流场的急剧变化而产生误差,根据文献[17]建议,从声屏障的两端,分别向两侧各延伸550 m,作为列车驶入声屏障前的加速段和驶出声屏障后的缓冲段,如图3所示。计算域的侧面和顶面定义为压力出口,底面、声屏障以及列车定义为无滑移壁面,由于高速列车与声屏障在空间上有相对位移,采用动态分层动网格技术实现列车网格在空间上的移动;因此,整个区域分为包含声屏障的静网格区域和包含高速列车的动网格区域,在计算过程中,动网格区域合并或分裂实现网格更新,静网格区域保持不变,在静网格区域与动网格区域之间设置交界面interface实现数据交换。动态分层网格技术通过设定分裂因子αs及 坍塌因子αc,并设置一个网格高度值h0作为参照实现。当包含高速列车的动网格区域向前运动时,动网格区域后边界的网格受到拉伸,当与其边界相邻的网格高度满足式(1)时,将根据指定的网格高度分裂网格;同时,动网格区域前边界的网格受到压缩,当与其边界相邻的网格高度满足式(2)时,与前边界相邻的网格被压缩,并与相邻的网格合 并。本次模 拟中αs取 值为0.4,αc取值为0.2,h0取值为1 m。

图3 计算区域Fig. 3 The calculation domain
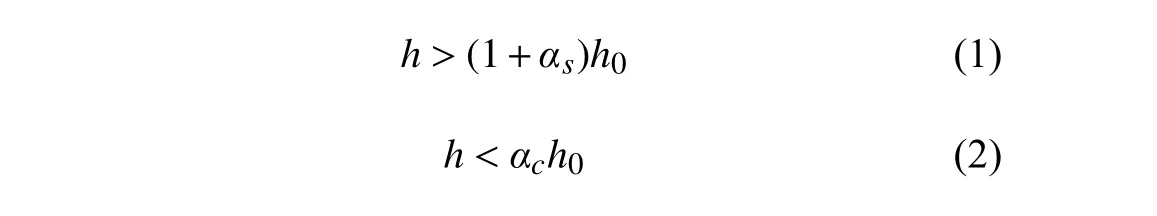
1.3 网格划分
采用ANSYS ICEM软件划分网格,为了捕捉到边界层附近的流体运动情况,提高模拟精度,对声屏障壁面附近以及靠近列车区域的网格进行加密,而远离研究对象的外部区域网格适当稀疏[16]。列车表面网格最大尺寸为0.1 m,声屏障表面网格最大尺寸为0.3 m,全局网格最大尺寸为5 m,总网格数为2400万,高速列车和声屏障表面网格情况见图4。通过对比细网格(3600万)和粗网格(2400万)的计算结果进行网格无关性检验,图5给出了利用两种网格计算得到的列车以350 km/h通过声屏障时距声屏障入口110 m处测点的压力时程曲线,两种网格计算得到的压力变化幅值分别为2269 Pa和2251 Pa,相差0.8%,说明采用网格量为2400万的网格既能满足计算精度的要求又能提高计算效率。

图4 高速列车和声屏障表面网格Fig. 4 Surface meshes of the high-speed train and the enclosed sound barrier

图5 不同网格量计算得到的压力时程曲线Fig. 5 The grid convergence test
1.4 计算方法
高速列车通过圆形全封闭声屏障时,声屏障内空气受壁面的限制无法自由流动,列车进入后,空气会受到声屏障壁面和车体的强烈挤压,需考虑空气的压缩性。因此,本文采用非定常、黏性、可压缩N-S方程和RNGk-ε湍流模型来模拟高速列车通过圆形全封闭声屏障的运行过程[20-22]。RNGκ-ε模型的湍流动能和耗散率方程如下所示:

式 中,模 型 常 数C2=1.68、Cµ=0.085、 σk=0.7179、σε=0.7179;;η=Sk/ε;η0=4.38;β=0.012[23]。
利用流体计算软件Fluent进行计算,采用SIMPLEC方法求解,计算 时间步长取0.002 s,CFL = 流速×1.9444,1 < CFL < 5,数值稳定性较好。
1.5 模型验证
采用文献[24]中的动模型试验对本文使用的数值模拟方法进行验证。按照上文中的方式对试验模型进行网格划分与数值计算,数值模拟得到的靠近试验段中间的PT2号测点的压力系数与试验结果对比如图6所示。

图6 动模型试验与数值模拟计算结果对比Fig. 6 The comparison of pressure coefficients between the moving model test and the numerical simulation
由图6可以看出,本次数值模拟较为准确地得出了该测点的压力极值和有效反映了压力波动的规律,证实了本文所采用数值模拟方法的准确性。
1.6 测点布置
声屏障壁面测点截面布置如表1所示,距入口50 m处开始布设风压监测截面,随后每50 m增加1处监测截面,声屏障中间位置加密监测截面,前后每隔5 m增加1处监测截面,前后各增加2处,一共选取了19个截面。每个截面上左侧、右侧及顶部共布置3个测点,编号如图7所示,声屏障出口处微气压波测点位置如表2所示。
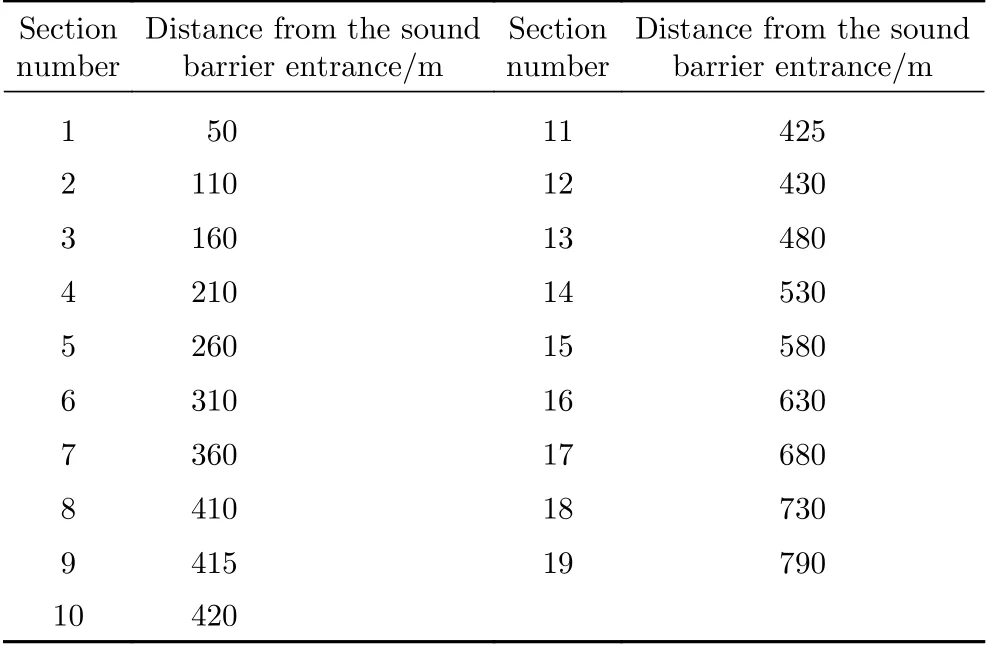
表1 声屏障壁面监测截面位置Table 1 Positions of monitoring cross-sections
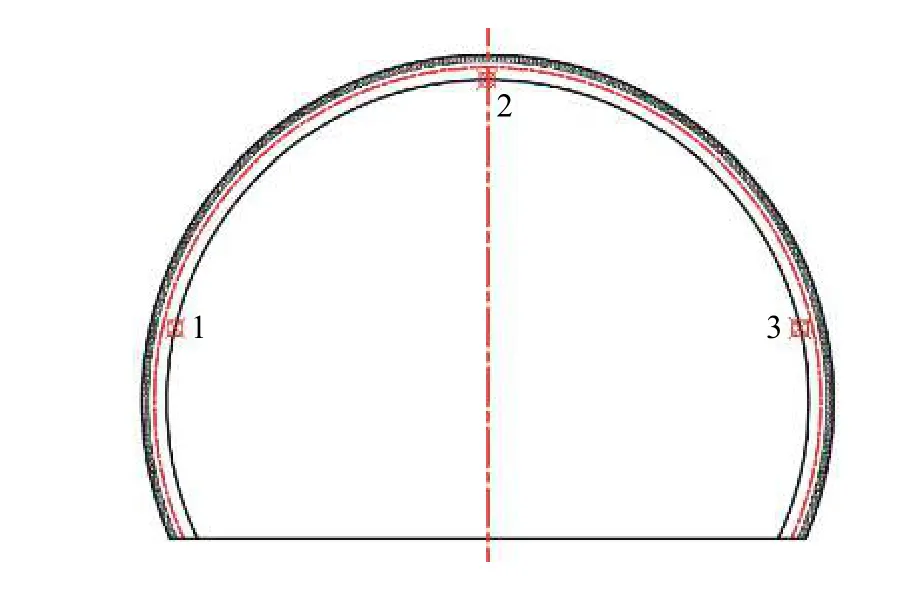
图7 声屏障壁面测点布置Fig. 7 The distribution of the measuring points on a monitoring cross-section
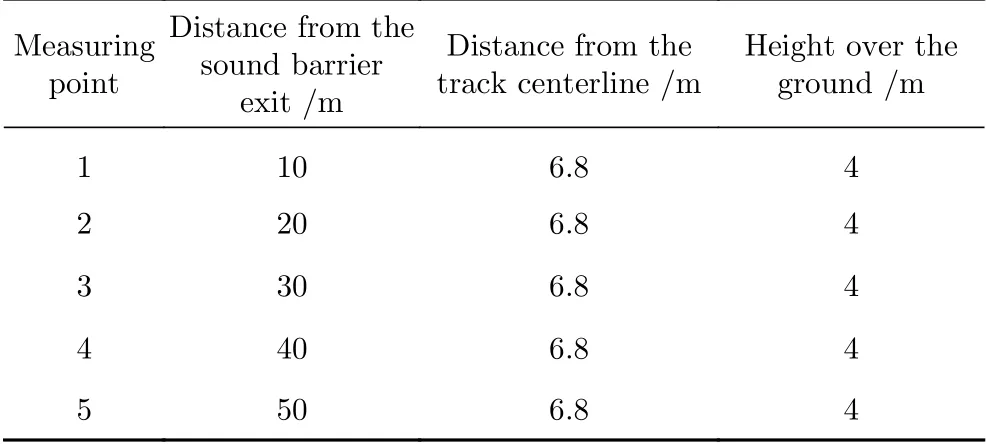
表2 微气压波测点位置Table 2 Positions of the measuring points for the micro-pressure waves
2 结果和讨论
2.1 单车压力波与会车压力波
单列高速列车以350 km/h速度驶入声屏障、两列高速列车以350 km/s的速度分别从声屏障两端相向驶入,车头驶入时产生压缩波,车尾驶入时产生膨胀波,相互叠加、干扰,在声屏障内部形成复杂的气动环境。图8给出了高速列车通过声屏障及在声屏障中央处交会时,声屏障中央测点的压力时程曲线、列车运行迹线及压力波传播轨迹,图8(a)、(c)表示单列车通过声屏障及两列车在声屏障中央会车时声屏障中央测点的压力时程曲线。图8(b)、(d)表示单列车通过声屏障及在声屏障中央会车时列车车头、车尾运行轨迹、压力波传播轨迹与时间的关系,图中红色实线表示车头运行轨迹,绿色实线表示车尾运行轨迹,黑色实线表示压缩波的传播轨迹,黑色虚线表示膨胀波的传播轨迹。
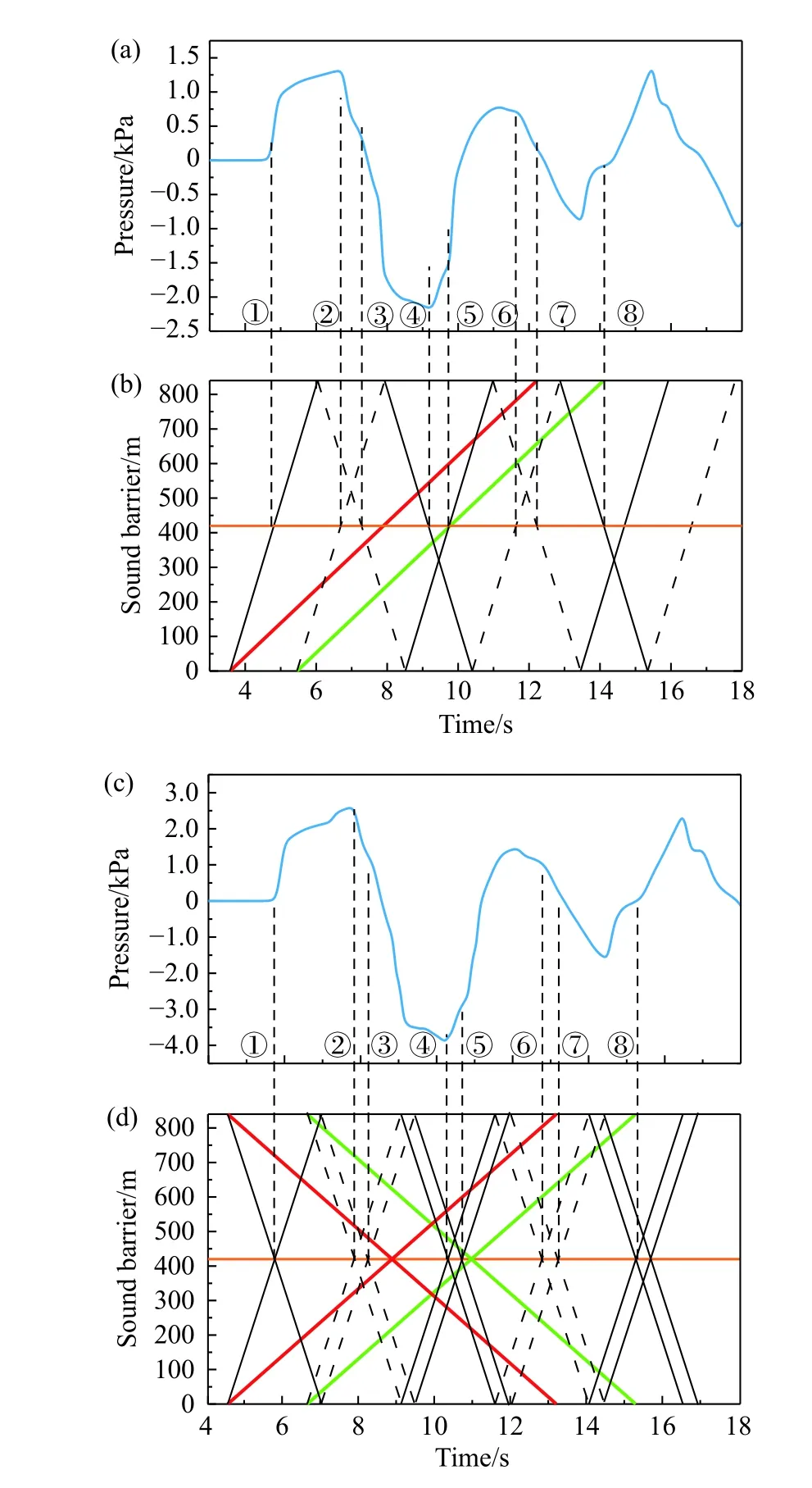
图8 声屏障中央测点的压力时程曲线Fig. 8 Pressure time histories at the center of the sound barrier
从图8(a)可以看出单列车驶入声屏障,车头产生一个压缩波,传至声屏障中央时,测点压力迅速上升(①时刻),车尾驶入声屏障时,产生一个膨胀波,传至测点时,测点压力出现最大值1298 Pa(②时刻),随后开始下降;压缩波传播到声屏障出口后反射回来的膨胀波传至声屏障中央,测点压力持续下降(③时刻),膨胀波传播到声屏障出口后反射回来的压缩波传至声屏障中央,测点压力出 现最小值−2153 Pa(④时刻),随后压力迅速上升;之后多个压缩波、膨胀波传至声屏障中央,测点的压力随之上升、下降(⑤、⑥、⑦、⑧时刻),此现象与隧道内列车压力波的传递[21]一致。
从图8(c)得知两列高速列车分别从两端同时相向驶入声屏障,车头产生的压缩波在声屏障中央测点处叠加,测点压力迅速上升(①时刻),随着车身逐渐驶入声屏障,测点压力不断增加,达到最大值2572 Pa,之后车尾完全驶入声屏障时产生的膨胀波在声屏障中央叠加,测点压力开始下降(②时刻);压缩波传播到声屏障出口、入口后反射回来的膨胀波在声屏障中央叠加(③时刻),两列车车头在中央交会,测点压力持续下降,出现最小值−3864 Pa,膨胀波传播到声屏障出口、入口后反射回来的压缩波在声屏障中央叠加(④时刻、⑤时刻),两列车车尾在中央交会,测点的压力逐渐上升;之后多个膨胀波、压缩波在声屏障中央叠加,测点的压力随之下降、上升(⑥、⑦、⑧时刻)。
2.2 声屏障延伸方向上壁面压力的变化
为了研究高速列车通过圆形全封闭声屏障时声屏障延伸方向上壁面压力的变化规律,比较了时速350 km/h的单列车通过声屏障时前七个截面2号测点的压力变化,如图9所示。从图中可以看出,当车头靠近截面测点时,该测点压力迅速上升;随后压力保持一段时间缓慢上升后迅速下降,离声屏障入口越远的截面,压力缓慢上升阶段持续的时间越长。这是因为当列车驶入声屏障时产生的压缩波以声速沿着声屏障向前传播,传播到截面上的测点时,测点压力迅速上升;车头经过时,测点压力迅速下降;由于压缩波传播的速度比列车行驶的速度快得多,所以距离入口较远的截面在出现极值压力前都有一段较为平缓的增加阶段。最大正压为1342 Pa,出现在车头即将到达第5截面;最大负压为−2041 Pa,出现在车尾刚经过第6截面。

图9 声屏障延伸方向上测点的压力时程曲线Fig. 9 Pressure time histories at the measuring points along the extension direction of the sound barrier
2.3 声屏障截面上各测点压力变化
图10给出了单列车以350 km/h的速度通过圆形全封闭声屏障时截面1各个测点的压力时程曲线。从图10中可以看出:截面1上各个测点压力的变化趋势相似,都在列车车头靠近该截面时(t= 4.02 s)出现正压极值,车尾远离该截面时(t= 6.08 s)出现负压极值,正压极值出现的时间与负压极值出现的时间相差2.06 s,该时间段内列车驶过的距离近似等于列车长度。表3给出了三个测点的正压极值、负压极值及压力变化幅值,测点1-2和1-3的压力极值比测点1-1分别低21%、28%,靠近列车测点的压力极值大于远离列车测点的压力极值。这与文献[25]中“列车流场对隧道横截面上近车侧测点压力变化的影响比对远车侧测点压力变化的影响要大”的结果一致。

图10 声屏障截面上测点的压力时程曲线Fig. 10 Pressure time histories at the cross-section of the sound barrier

表3 截面测点压力极值Table 3 Extreme pressure amplitudes at the cross-section of the sound barrier
2.4 车速对声屏障内压力变化的影响
图11为高速列车分别以200 km/h、250 km/h、350 km/h通过时,声屏障中央测点压力变化幅值和车头鼻尖压力最大值与车速的关系,结果显示压力变化幅值、车头鼻尖压力最大值与车速的二次方呈近似线性关系;采用幂函数曲线拟合得到的公式与文献[14]给出的列车穿过隧道时隧道测点压力变化幅值与车速的关系式(y=0.017x2.08)十分接近,与文献[25]报道列车驶过隧道时车头表面压力最大值与车速的二次方成正比十分吻合。
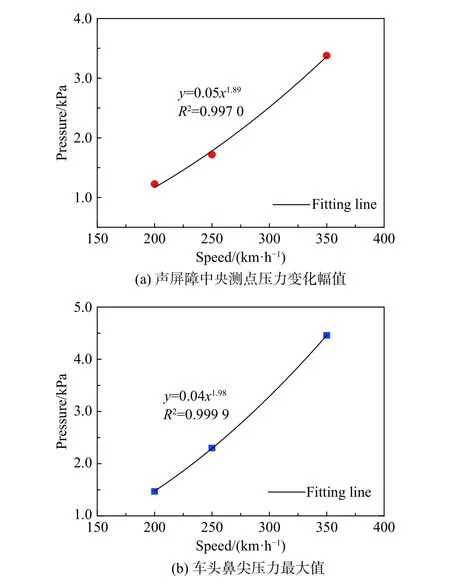
图11 声屏障中央测点压力变化幅值、车头鼻尖压力最大值与车速的关系Fig. 11 The relationships between (a) the pressure amplitude differences at the central of the sound barrier and (b) the maximum pressure amplitudes at the train head nose tip and the train speeds
2.5 车速对声屏障出口微气压波的影响
列车驶入声屏障时产生压缩波,压缩波以声速向前传播,传播到出口后,一部分以膨胀波的形式反射回来,另一部分向声屏障外辐射,形成微气压波。图12给出了单列车以350 km/h通过圆形全封闭声屏障时距声屏障出口10 m处测点的压力时程曲线、列车运行轨迹及对应的压力波传播轨迹图。从图12可见:列车进入声屏障产生的初始压缩波向声屏障外辐射,传至该测点时测点压力升高(①时刻),车尾产生的膨胀波传至该测点时其压力降低(②时刻),初始压缩波经二次反射传到该测点时测点压力升高(③时刻);列车驶出声屏障后,车头经过该测点时,测点压力迅速升高随即迅速下降(④时刻),车尾经过该测点时,其压力迅速下降然后迅速上升(⑤时刻)。这与文献[26]报道的列车以304 km/h通过隧道距隧道出口2.5 m处测点微气压波的发展规律一致。图13给出了当列车以200 km/h、300 km/h、350 km/h通过圆形全封闭声屏障时出口不同位置处测点微气压波的时程曲线。从图13可以看出:靠近声屏障出口的测点,其微气压波的极值大于远离声屏障出口的测点。测点距离出口40 m和50 m时,基本监测不到压力的变化,说明列车速度不超过350 km/h时,微气压波的传播距离小于等于40 m。图14给出了不同车速下,距离声屏障出口10 m处测点微气压波的时程曲线,从图中可以看出微气压波的波形随着列车速度的增大,其波峰越早出现,持续时间也越短,列车速度从200 km/h增加到350 km/h时,微气压波的极值从3.6 Pa增加到16.3 Pa。图15给出了微气压波极值与列车运行速度的关系,图中公式由幂函数曲线拟合得到,微气压波极值(y)与列车速度(x)之间的拟合公式为y=0.00000067x2.9,这表明列车以较高的速度通过声屏障时,产生的微气压波极值近似与列车速度的三次方成正比,说明列车的速度是影响微气压波强度的重要因素。
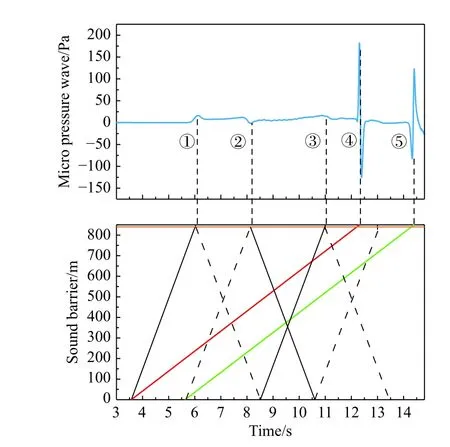
图12 距声屏障出口10 m处测点的压力时程曲线Fig. 12 Pressure time histories at the measuring points 10 m downstream of the sound barrier exit
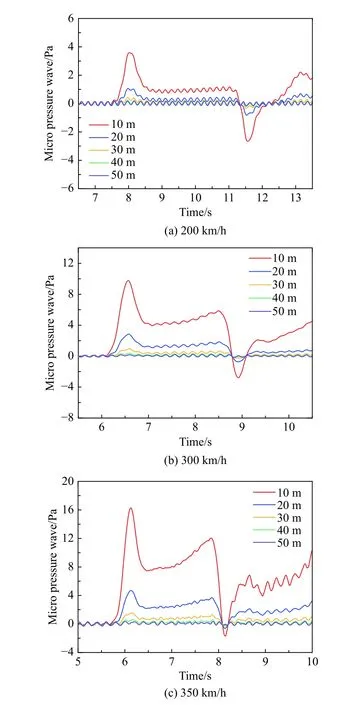
图13 不同速度下的微气压波时程曲线Fig. 13 The time histories of micro-pressure waves generated by trains with different speeds
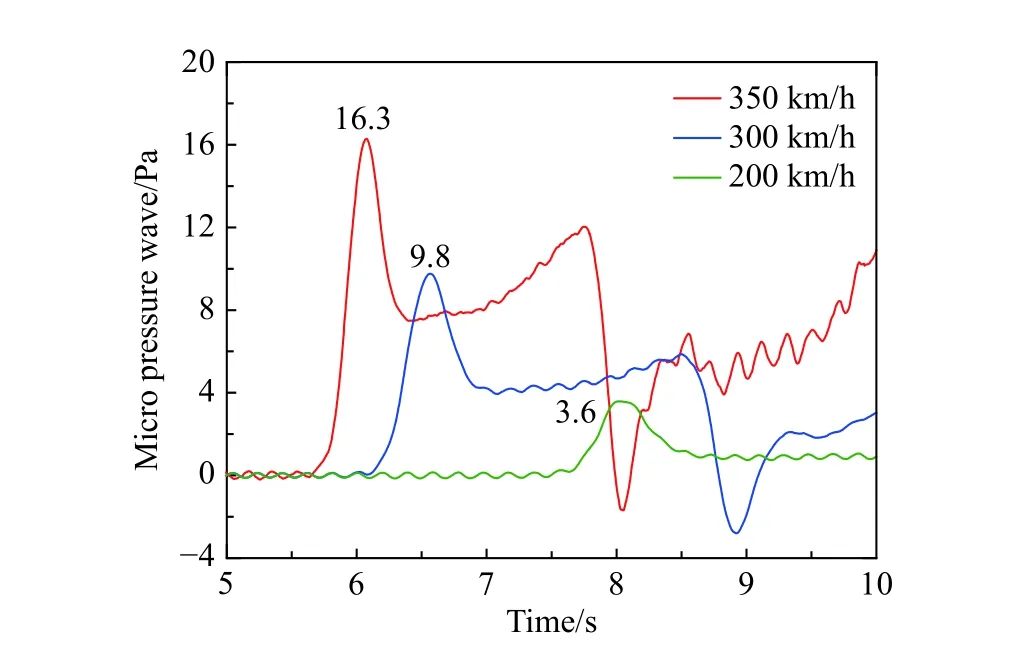
图14 不同速度下距声屏障出口10 m处测点微气压波时程曲线Fig. 14 The time histories of micro-pressure waves measured at points 10 m downstream of the sound barrier exit. Lines with different colors represents results by trains with different speeds
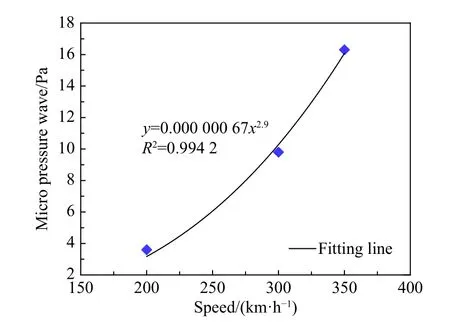
图15 微气压波极值与车速的关系Fig. 15 The relationship between extreme amplitudes of micro-pressure waves and train speeds
3 结论
本文通过对高速列车通过圆形全封闭声屏障产生的压力波与微气压波进行数值模拟研究,得到结论如下:
1)列车通过圆形全封闭声屏障时,声屏障壁面风压变化与隧道结构风压变化十分相似;其时变特性与压缩波和膨胀波的产生、传播及反射有关;压缩波传播到壁面测点时压力上升,膨胀波传播至壁面测点时压力下降。
2)在声屏障横截面上,距离列车表面越近的测点压力极值越高,同一截面的风压极值差异最大为28%;因此,在全封闭声屏障结构设计时需考虑风压荷载非均匀分布的工况。
3)列车通过全封闭声屏障时将产生微气压波,其产生的原理与隧道出口微气压波类似;而且,列车速度不超过350 km/h时,微气压波的传播距离小于等于40 m;微气压波极值与列车速度的三次方近似呈正比关系。
