沟槽微结构尺寸对高速列车横风特性影响研究

王业腾，孙振旭，*，鞠胜军，王梦莹，杨国伟

(1. 中国科学院力学研究所 流固耦合系统力学重点实验室，北京 100190；2. 中国科学院大学 工程科学学院，北京 100084)

0 引言

当高速列车在横风环境中运行时，其气动性能会显著恶化，严重时就会引发翻车事故。比如，1981年，印度一辆旅客列车在飓风的影响下摔落桥底，致使800多人死亡。因此，系统地研究横风作用下列车的气动特性显得尤为重要。数值模拟已被广泛应用于各个工业领域[1-3]，是高速列车空气动力学的主要研究方法之一，具有低成本、高效率等优点。Ben通过数值模拟得到了高速列车在不同角度横风作用下的气动升力[4]。Justin 等采用不同的湍流模型对列车受侧风作用时周围的流场进行了数值模拟[5]。刘荣等基于气动力和力矩数值结果，对高速列车临界倾覆风速进行了研究[6]。公衍军等建立了三维高架桥-列车耦合模型，并进行了列车速度和风速耦合作用下的数值模拟[7]。

为改善横风作用下高速列车的气动特性，学者们开始探索适用的优化方法。目前，常用于高速列车气动外形优化设计的方法大多围绕宏观尺度展开，但由于实际工程中的诸多限制，这类方法带来的增益效果已接近极限，需要从新的角度出发探寻提升列车气动性能的有效途径。因此，有学者试图从微观角度出发，探索提高高速列车气动性能的新途径。汪久根等设计并研究了不同类型微结构表面的降噪效果[8-9]。苗秀娟发现在列车顶部加肋可以帮助降低表面压力[10]。孙朋朋等分析了不同类型微结构的设计参数对高速列车气动阻力的影响[11]。朱海燕等和唐焜等分别研究了具有球窝和凸壳的非光滑表面的减阻机理[12-13]。基于现有研究，微结构主要用于高速列车的减阻降噪。关于微结构如何影响高速列车侧风气动性能，目前尚无相关文献报道。Browand等在他们的研究中提到，微结构设计可能对车体的稳定性有很强的影响[14]。因此，评价微结构设计参数对高速列车横风稳定性的影响是一个重要课题，本文从数值模拟出发研究微结构影响列车横风特性的机理并分析微结构设计尺寸与列车侧向力/倾覆力矩之间的影响关系。

实验常被用来探索和证实科学的规律。然而，随着科学技术的快速发展，试验涉及的因素越来越多，各个因素间的关系也越来越复杂，光凭经验已无法实现预期目标，故出现了试验设计这一概念。目前，常用的试验设计方法包括：全面试验设计、正交试验设计、均匀试验设计、回归试验设计及混料试验设计。其中，正交试验设计是最早引入我国的试验方法，并在流体力学实验领域得到了广泛应用。例如范泽兵等采用正交试验设计，以总进气压力、功率分流、工作方式和节气门杠杆位置为试验因素，对发动机稳态性能进行评价[15]。程效锐以进水口宽度、叶片轴向长度、叶片与出水口轴向距离为试验因素，基于正交设计方法，优化潜水泵叶片的形状[16]。

本文以390级Pendolino列车的1∶25缩尺模型为原型，通过在头车顶部增加矩形条，设计了非光滑表面。第1节介绍本文采用的数值算法、计算模型、计算域和边界条件，并通过与风洞实验分析比较，验证数值模拟方法的正确性。第2节从涡量分布和壁面剪应力分布出发，分析微结构改善列车横风特性的机理。第3节采用正交试验设计与统计分析结合的方法，分析矩形条带设计参数与列车侧向力/倾覆力矩之间的敏感性，并给出条带外形设计的优选方案。最后第4节对研究进行总结，列出主要研究成果，并对今后的工作提出建议。

1 数值模拟

1.1 数值算法

本文采用商业软件STAR-CCM+研究高速列车在横风作用下的空气动力学性能。控制方程为三维不可压缩N-S方程，采用有限体积法离散。对于时间离散，采用二阶隐式格式。同时，为了提高计算精度，在空间离散方面，分别采用二阶中心差分格式、二阶迎风格式对控制方程的粘性项和非粘性项进行离散。此外，基于SSTk-ω两方程模型的改进延迟分离涡模拟（IDDES）方法将用于模拟表面光滑和粗糙的高速列车周围流场。

Spalart等在2014年提出了分离涡模拟（DES）方法[17]。DES结合大涡模拟（LES）方法和雷诺平均Navier-Stokes （RANS）方法，可以在保证计算精度的同时减少计算时间。这种方法多用于解决大规模分离流动问题，但不具有通用性，仍然存在一些问题，比如网格敏感性问题会导致非物理分离现象的出现。为了解决这些问题，Mikhail等提出了延迟分离涡模拟（DDES）方法，即在DES模型中加入延迟函数，使得RANS向LES转换的速度变慢[18]。

但使用DDES进行模拟时，DDES模型中会出现RANS和LES所解得的对数区斜率不同的情况，从而导致对边界层效应敏感的分离流受到较大干扰。因此，提出了一种改进的延迟分离涡（IDDES）方法，该方法能够有效处理对数区内同时由RANS和LES求解的网格，大大降低网格相关性。该方法在高速列车横向风稳定性研究中得到了广泛应用。例如，Munoz等采用该方法对受横风作用的高速列车周围流场进行了数值模拟[19]。通过分析，他们发现这种方法能够捕获剪切层中的小涡。Li等利用该方法得到了高速列车在侧风作用下的表面压力和气动力，与试验结果吻合较好，表明该方法能够准确预测列车周围的平均流场[20]。

1.2 计算模型和计算域

本文采用计算模型源于伯明翰大学的风洞模型，分为光滑模型和粗糙表面模型两种。研究的横风场景为风洞中的横风场景，即列车不动，来流垂直于列车轴线方向。这样做的目的是一方面方便与风洞实验结果对标，确定数值方法和网格的准确性；另一方面，基于粗糙模型采用的条带结构进行参数化研究，通过灵敏度分析确立关键设计参数，并确立最佳参数尺寸。研究结果可以为风洞模型下条带的最佳设计提供理论指导。本文光滑表面列车模型为390级Pendolino列车的1∶25比例模型，包括一节头车和一节半挂车。为提高计算效率，在不影响计算结果的前提下，对列车转向架、空调机、受电弓及风挡等区域进行了简化，且不考虑天线、车门、车窗、底部悬浮架等零部件对列车气动性能产生的影响。

数值模拟计算外场区域与风洞实验段一致，如图1黑框所示。从图1可以看到，计算模型除了列车模型外，还包括一条单轨轨道及一块分隔板。值得注意的是，分隔板固定在计算域侧壁，且距地面约0.3 m，这样做的目的是消除地面效应对列车周围流场产生的干扰。

图1 计算域Fig. 1 Computational domain

通过在前车顶部的两个区域添加矩形条，得到一个表面粗糙的模型，如图2所示。每个区域有15条带状，相邻两条带状之间的距离相等。图3显示了矩形条的几何形状。所有条带截面积相同，但不同区域条带长度不同。区域1的条带长度为0.12 m，区域2的条带长度为0.24 m。

图2 非光滑计算模型Fig. 2 Computational model with a rough surface

图3 矩形条带的几何尺寸Fig. 3 The geometry of a rectangular strip

1.3 边界条件

边界条件如图4所示。除进出口边界外，其他边界均规定无滑移壁面条件。速度入口的气流速度为7.2 m/s，方向沿x轴负向；压力出口压力值为0。在计算过程中，列车模型、轨道及分隔板始终保持静止，并受到具有90°风向角的相对风作用。

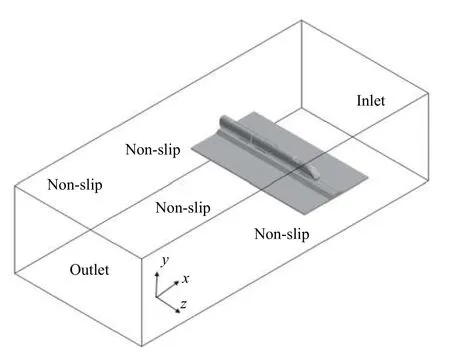
图4 边界条件Fig. 4 Boundary conditions

1.4 计算网格

本文使用切割体网格生成器进行空间网格划分，以正交切体六面体网格为主。由于近壁区具有明显的边界层效应，为更好地反映车体周围的流场结构，可以在列车壁面进行棱柱层网格生成，主要为三棱柱网格和金字塔网格。先以1.1的增长比生成了10层棱柱层网格，由此尺寸确定的无量纲壁面距离y+约为1.13，满足壁面函数的要求。

为捕捉高速列车周围流场的更多细节并保证计算精度，在车身附近区域进行了网格加密，设置了三个加密区，即图中区域A2、A3和A4，网格尺寸分别为0.0024 m、0.0048 m和0.0192 m。图5分别给出了x= 0截面和z= -0.38截面上的网格分布示意图。在此基础上，进一步细化了头车顶部加设条带区域的网格，如图中区域A1所示，该区域内网格尺寸为0.0006 m。此外，图6给出了条带附近的网格分布示意图。从局部放大图可以看到，条带表面也生成了棱柱层网格，如区域P所示。同时，条带的几何外形在网格生成过程中并未遭到破坏，证明所用网格划分方案确能保证较高质量的计算网格。

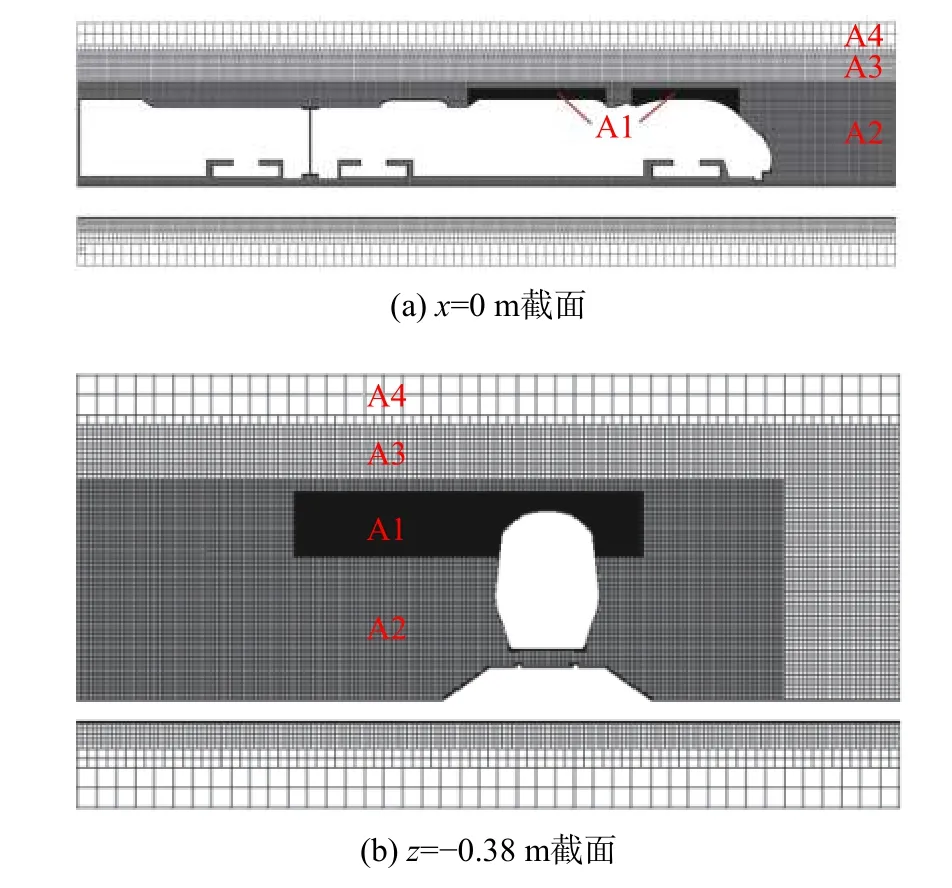
图5 不同截面上的计算网格分布示意图Fig. 5 Grids on different sections

图6 条带区域计算网格局部放大图Fig. 6 A partially enlarged view of the grids around the strip area

1.5 方法验证

Hashmi等[21]在伯明翰大学风洞中完成了图1和图2所示模型的实验。他们得到了列车不同回路上某些点的压力系数Cp，所有回路的位置如图7所示。无量纲压力系数Cp的可定义为：

图7 所有回路位置Fig. 7 The position of all loops

其中，p为局部静压，p0为来流总压，ρ =1.184 kg/m3为来流密度，Vref=7.2 m/s为来流速度。

图8给出了环E和G上压力系数数值计算结果与实验结果的对比。本文采用笛卡尔网格进行空间网格划分，生成粗糙网格和精细网格两组网格。前者网格数量为5.216×107，后者网格数量为8.887×107。从图中可以看出，采用不同网格方案得到的压力系数分布是一致的，但与实验结果对比时，明显看出采用精细网格的方案计算精度更高。因此，所有后续的计算都以与精细网格一致的方式划分网格。

图8 回路E和G上数值计算和实验结果所得到的压力系数比较Fig. 8 The numerical and experimental results of the pressure coefficient on the loops E and G

1.6 气动载荷特性

侧向力和倾覆力矩是评价高速列车在侧风作用下稳定性的重要指标。为简化分析，对侧向力系数Cs和 倾覆力矩系数Cmz进行定义：

其中，Aref是参考面积，也就是列车在x方向的投影面积，取为0.1232 m2[22]；Href是车厢高 度，为0.156 m；Fs是侧向力，以沿x轴正向为正；Mz是倾覆力矩，力矩 中 心 在（0,0.07155,0）处；ρ为 来 流 密 度，取 为1.184 kg/m3；Vref为来流速度，即7.2 m/s。

图9给出了横风作用下光滑表面列车和非光滑表面列车的Cs和Cmz的计算结果。与光滑表面列车模型的比较，非光滑表面列车模型的侧向力系数Cs和倾覆力矩系数Cmz分别减小了3.71%和10.56%，表明局部矩形沟槽表面设计在一定程度上确实利于提升高速列车的横风稳定性。

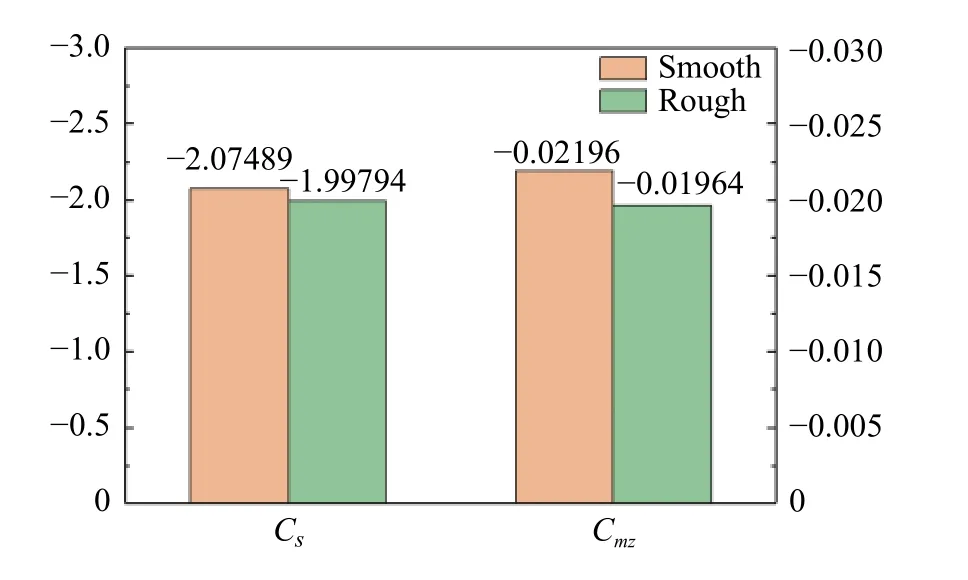
图9 光滑表面模型和粗糙表面模型的Cs和Cmz的计算结果Fig. 9 Cs and Cmz on models with smooth and rough surfaces

2 沟槽微结构流场控制机理

将微结构作用于具有复杂几何外形的高速运动物体表面，绕体气流的运动规律较之平板边界层会发生显著变化。非光滑表面列车能够减小的侧向力和倾覆力矩的原因是小矩形条带抑制了流动分离，使得气流能够以更加稳定的状态在列车表面运动。为进一步探究微结构减弱侧向力和倾覆力矩的机理，本节比较光滑表面列车模型和粗糙表面列车模型的涡量分布与壁面剪应力分布。

2.1 涡量分布比较

选择以图7的G回路截面为研究对象，分析车体周围的涡流特性，图10分别给出了光滑表面列车模型和粗糙表面列车模型中所选截面上的涡量分布云图，图中不同颜色代表不同的涡量幅值范围。可以看到，不论是光滑表面列车模型还是粗糙表面列车模型，气流在迎风面拐角处都会形成强度极高的涡结构，这些涡结构将沿约135°的方向向背风面运动。

图10 涡量分布云图Fig. 10 Contours of vorticity magnitude at loop D with (a)smooth and (b) rough surfaces

对比图10（a、b）可以发现，光滑表面列车模型顶部的高强度涡最初是紧贴壁面运动的，而矩形条带能使其偏离壁面一段距离运动，起到削弱边界层内湍流变化的作用。同时，条带的阻断作用能够减少由湍流运动引起的瞬时横流，并促使大型涡结构分裂为较小的涡结构，从而使涡量幅值显著降低。具有适当高度的条带对车体周围的涡结构起到了阻挡作用，使得湍流过渡出现了延迟。当车体周围的大尺寸涡结构被条带分解时，边界层内部的能量交换加剧，使涡结构原有的能量在一定程度上得到衰减，同时涡结构产生的吸力作用也大大减小，这有助于提升列车的横向稳定性。与粗糙表面列车模型相比，光滑表面列车模型周围的涡流强度更强且涡核尺寸更大，这是导致其气动性能较差的关键因素。

此外，从图10还可以看到，由于转向架和轨道的影响，列车底部来流形成的涡结构也会具有较大强度。当来自顶部和底部的两股气流相遇时，列车背风面将出现复杂的涡量分布特性。与光滑表面列车模型进行对比分析后不难发现，粗糙表面列车模型背风面涡结构的数量有所减少且涡量幅值也得到了一定程度上的衰减。造成这种现象的主要原因是，矩形条带减弱了边界层内部的湍流变化，使得流经列车顶部的气流能够更加稳定地向背风面运动，如此一来气流交汇时产生的扰动作用也会随之减小，从而降低背风面流场的复杂程度。

2.2 壁面剪应力

壁面剪应力，是反映车体表面粘性作用的关键物理量。图11为头车壁面剪切应力分布云图，图中不同颜色代表壁面剪应力幅值 τw的不同取值范围。可以看到，当来流垂直作用于列车侧壁时，在迎风面形成的 τw极 小；随着气流向顶部运动， τw的值逐渐增大，并在迎风面与顶部的交界处达到最大值；气流通过流动分离区后， τw又将逐渐减小并趋于稳定。对比图11（a）和图11（b）不难发现，在矩形条带的影响下，列车迎风面拐角处及顶部区域内的 τw值将显著减小，意味着车体表面粘性作用受到了抑制，其对气动载荷（比如侧向力）造成的影响也会随之减小，从而达到提升列车横风稳定性的目的。

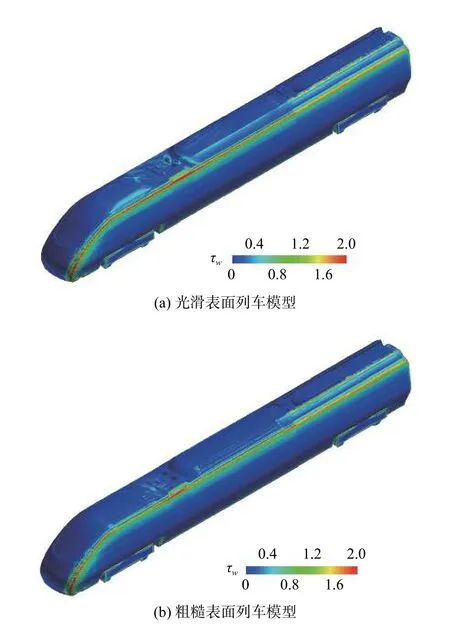
图11 壁面剪应力分布云图Fig. 11 Contours of the wall-shear stress at (a)smooth and (b)rough surfaces

3 非光滑表面列车横风性能灵敏度分析

在列车上表面安装矩形条带可以抑制气流流动分离，进而改善列车的气动特性。当矩形条带长度方向与横风作用方向垂直时，其几何尺寸会直接影响车体周围的流场特性。

因此，为研究附加矩形条带几何参数对高速列车横风稳定性的影响，本文首先采用正交试验设计方法生成原始样本，然后通过计算流体力学（CFD）仿真软件进行高精度的气动力/力矩系数计算，最后结合方差分析和极差分析两种统计分析方法完成矩形条带几何设计参数的灵敏度分析。

3.1 正交试验设计

本文正交试验设计以列车模型的侧向力系数Cs和 倾覆力矩系数Cmz为试验指标，选取矩形条带的四个几何参数L1、L2、W和H作为设计变量，各参数的意义及取值见表1。

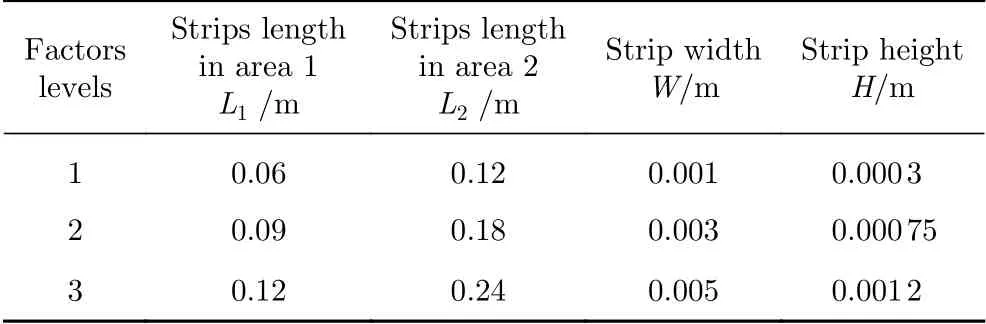
表1 试验因素及其水平Table 1 Experimental factors and their levels

每个试验因素均取三个值作为其试验水平。根据试验因素及其水平，选择使用L18（38）正交表进行方案设计。需要注意的是，本文的所有设计列数中，前4列为试验的设计变量列，后4列为随机误差列。对每个设计方案分别进行数值模拟，采用的计算方法、计算域、模型位置、网格划分方式及边界条件等均与上一节相同。表2列出了所有试验方案，并在最后两列给出了各个方案侧向力系数Cs和倾覆力矩系数Cmz的计算结果。

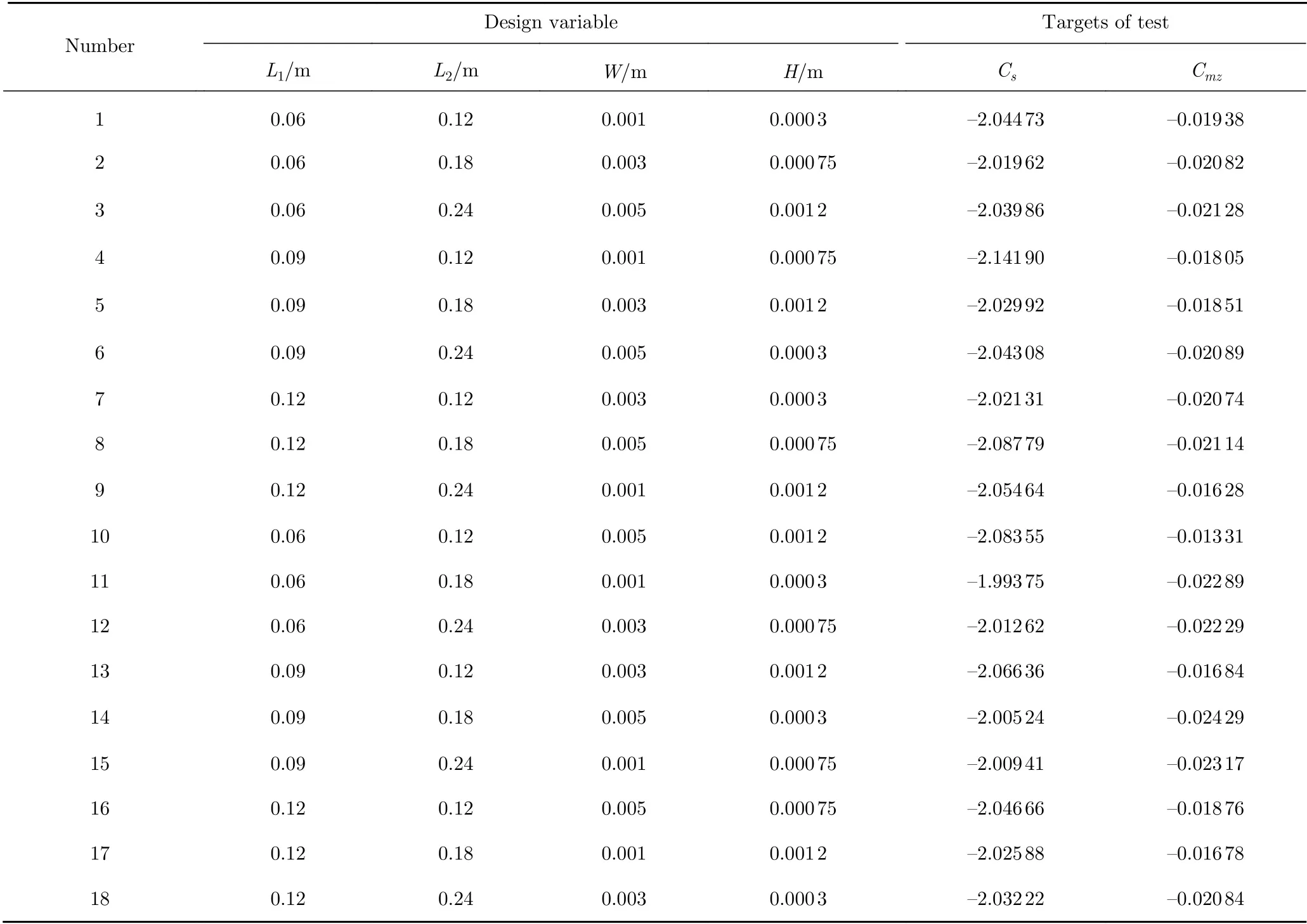
表2 试验方案及数值计算结果Table 2 Cs and Cmz for rough surfaces with different strip shapes

3.2 方差分析

方差分析技术作为一种统计方法可以用来分析不同观测条件下实验结果的差异[23-25]，评价各因子对试验指标的影响程度。其基本思想是：将数据的总波动分解为由因素水平变化引起的波动和由误差引起的波动两部分，然后构造出F统计量进行F检验，以判断各个因素对评价指标的影响是否显著。

表3和表4分别给出了侧向力系数和倾覆力矩系数的方差分析结果。df表示自由度，SS表示偏方差和，MS表示方差，F表示各因素的方差和与实验误差的方差的比值，通常将空列的偏差平方和视为实验误差的方差，P表示F统计量对应的显著性水平。一般情况下，在方差分析中，“显著”置信水平常取为0.05，而“极显著”置信水平常取为0.01。

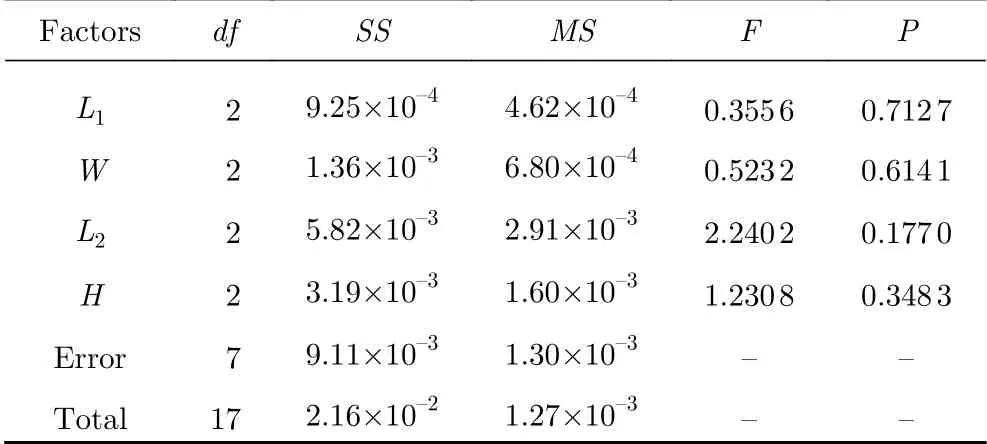
表3 侧向力系数C s的 方差分析结果Table 3 Results of the variance analysis for the side force coefficient Cs

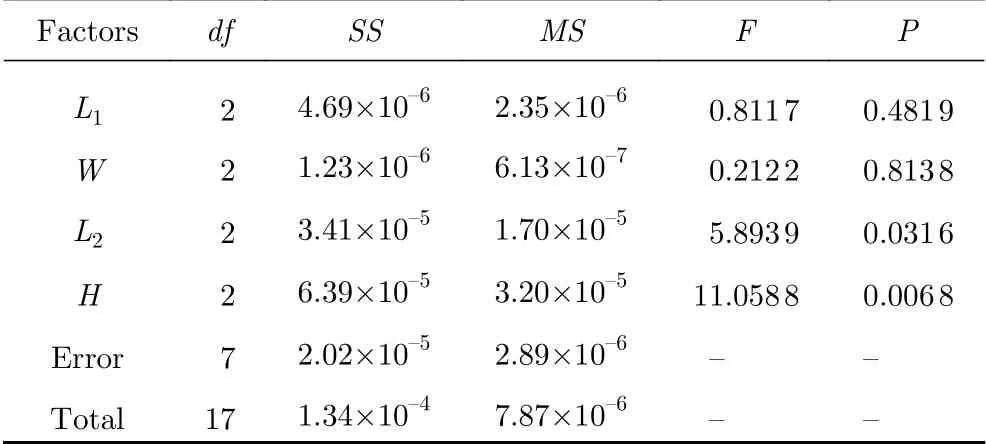
表4 倾覆力矩系数C mz的 方差分析结果Table 4 Results of the variance analysis for the roll moment coefficient Cmz

由表3可以看到，与区域1中矩形条带的长度L1、区域2中条带的长度L2、条带宽度W及条带高度H的F值对应的显著性水平p均大于0.05，表明这四个设计变量对侧向力系数Cs的影响都不显著。但相比之下，区域2中条带的长度L2及条带高度H对侧向力系数Cs的影响效果较之另外两个设计变量要明显一些。

由表4给出的倾覆力矩系数Cmz的方差分析结果，不难发现，与区域2中条带的长度L2及条带高度H的F值对应的显著性水平p均小于0.05，意味着这两个设计变量对倾覆力矩系Cmz有显著影响，而另外两个设计变量的影响并不显著。此外，值得一提的是，与条带高度H的F值对应的显著性水平p小于0.01，说明条带高度H对倾覆力矩系数Cmz影响是极显著的。

基于上述分析结果，按照F值的大小对四个试验因素的影响效果进行排序：就Cs而言，L2的影响最明显，H次之，接着是W，最后是L1；对于Cmz，H的影响效果变为明显，其次是L2，然后是L1，而W的影响效果最弱。因此，在进行矩形条带外形设计时，应以区域2中条带的长度L2及条带高度H为重点优化对象。

3.3 极差分析

为评价各因子对试验指标的影响程度，可以对数据进行极差分析，其基本思想是：将数据的总波动分解为由因素水平变化引起的波动和由误差引起的波动两部分，然后构造出F统计量进行F检验，以判断各个因素对评价指标的影响是否显著。

极差分析包括计算和判断两个步骤，可按如下流程完成分析：

1）计算Kjm、和Rj，并将结果记录在表5中。Kjm为第j列因素第m水平所对应的试验指标和；K¯jm为第j列因素第m水平所对应的试验指标平均值；Rj为第j列因素水平下的最大平均值和最小平均值的差值，反映了第j列因素水平波动时试验指标的变化幅度。

表5 极差分析结果Table 5 Results of the range analysis

2）根据极差Rj的大小，可以判断试验因素对试验指标影响的主次顺序。Rj越大，说明该因素水平变化时对试验指标的影响越大。由表5计算结果可知：对于侧向力系数Cs，各因素主次顺序为L2＞H＞W＞L1；而对于倾覆力矩系数Cmz，各因素主次顺序为H＞L2＞L1＞W。因此，L2和H为主要因素，L1和W为次要因素，这与方差分析结论完全一致。

4）为提升高速列车横风稳定性，两个试验指标的绝对值必然是越小越好，也就是说K¯j1、K¯j1、K¯j1需取最大值。此外，由于L1和W是次要因素，可固定为原值成为约束条件，即L1= 0.09 m，W= 0.003 m，则只需根据图12趋势曲线确定L2和H的优选水平组合。由图12（a）可知，对于侧向力系数Cs，L2和H的优选水 平 组 合 为L2= 0.18 m、H= 0.00075 m；而 从图12（b）可以看出，对于倾覆力矩系数Cmz，L2和H的优选水平组合为L2= 0.12 m、H= 0.0012 m。

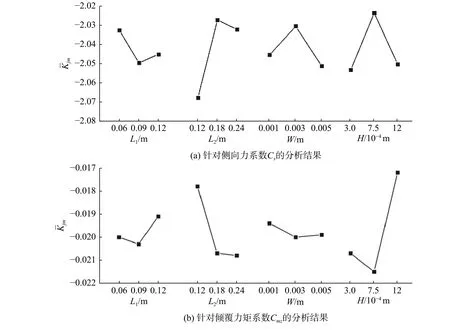
图12 因素与指标关系趋势曲线Fig. 12 Trend curves of the relationship between factors and indicators

5）由于两个试验指标单独分析得到的优选水平组合不一致，可结合综合平衡法确定最终优选方案。L2对侧向力系数Cs的影响大小排第一位，对倾覆力矩系数Cmz的影响大小排第二位，故选择L2= 0.18 m。H对侧向力系数Cs的影响大小排第二位，对倾覆力矩系数Cmz的影响大小排第一位，故选择H=0.0012 m。因此，初步预测当区域1中条带的长度L1取0.09 m、区域2中条带的长度L2取0.18 m、条带宽度W取0.003 m、条带高度H取0.0012 m时，能对高速列车侧向力系数Cs和倾覆力矩系数Cmz起到较好的优化作用。

所得优选水平组合对应正交试验设计的方案5，表6给出了原值方案与优选方案的侧向力系数Cs和倾覆力矩系数Cmz的计算结果。优选方案的条带高度较之原值方案增加了60%。可以看到，与原值方案相比，优选方案的侧向力系数Cs的值增加了0.80%，而倾覆力矩系数Cmz的值减少了6.14%。由于倾覆力矩系数Cmz是造成列车倾覆的最主要原因，从综合性能来看，该优选方案确实具有提升列车横风稳定性的作用。

表6 原值方案与优选方案计算结果对比Table 6 Comparison of the original and optimized schemes

4 结论

本文采用基于SSTk-ω两方程模型的IDDES方法，论证了矩形条对受侧风作用的高速列车气动性能的影响，并结合正交试验设计，采用方差分析法和极差分析了矩形条几何参数的影响。得到如下结论

1）与光滑模型相比，粗糙模型可使列车侧力系数和倾覆力矩系数分别降低3.71 %和10.56 %，从而提高列车的横风稳定性。

2） 矩形条带可以抑制气流流动分离，促使大尺寸涡结构分解为众多小尺寸涡结构。在此过程中，边界层内部的能量交换加剧，使涡结构中的能量得到衰减，减小了近壁区内的湍流扰动和车体表面粘性作用，保证低速气流能够更加稳定地发展，以达到提升列车横向稳定性的目的。

3）采用方差分析方法和极差分析可以准确分析矩形条的几何参数对横风作用下高速列车气动性能的影响。在利用矩形条带参数优化进行高速列车横风气动外形设计时，需重点关注两个主要参数，即区域2中条带的长度L2和条带高度H，而区域1中条带的长度L1和条带宽度W为次要因素，对列车横风性能的影响很小，在非必要时可以忽略。

4）通过极差分析得到了矩形条带的优选参数设计方案，即区域1中条带的长度L1取0.09 m、区域2中条带的长度L2取0.18 m、条带宽度W取0.003 m、条带高度H取0.0012 m。数值计算结果显示，与原值方案相比，优选方案的侧向力系数Cs增加了0.80%、倾覆力矩系数Cmz减少了6.14%，表明该方案确能有效改善高速列车气动性能。

上述结论可为后续高速列车侧风气动优化设计提供新的思路。然而，目前的研究主要集中在风洞实验中的缩比模型上，由于风洞中列车模型静止，因而本文研究横风作用与实际运行场景下的横风作用存在一定差异。微结构表面在实际运行中如何影响高速列车的气动性能尚不确定，这将是我们今后研究的主要目标。