电力巡线无人机航拍图像匹配算法研究

马耀名，陈艺琳，李万禹

辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛125105

随着无人机技术的发展，使用无人机对输电线路巡检已成为必然趋势，使用电力巡线无人制作输电线路全局图像、电网三维实景、故障检测已成为热门研究方向[1-6]。图像匹配技术是输电线路图像拼接、三维重建的主要步骤，直接影响图像拼接和三维重建效果。电力巡线无人机拍摄的输电线路图像具有几何畸变较大、相邻图像重叠高、光照不均匀等特点[7-8]，致使航拍图像匹配难度较高。

目前电力巡线无人机输电线路影响匹配算法主要是基于局部特征的匹配算法，其核心是特征检测和描述符构建。基于局部特征的图像匹配算法可分为三大部分：一是尺度空间构建，二是局部特征提取，三是特征编码。SIFT算法（Scale Invariant Feature Transform）[9]利用高斯滤波构建尺度空间，然后再高斯差分金字塔中检测特征点，最后建立128维浮点型描述符；该算法具有较好的抗噪声、视角变换等能力，但描述符维度较高严重影响算法效率。针对SIFT算法效率较低，提出了利用小波算法建立64维浮点型描述符的SURF算法[10]（Speeded Up Robust Feature），该算法稳定性与SIFT算法相似，效率提升了10倍左右。SIFT算法和SURF算法的描述符均为浮点型，由于计算不同描述符相似性耗时较长，故提出了ORB算法[11]（Oriented FAST and Rotated BRIEF），该算法利用FAST算法[12]（Features from Accelerated Segment Test）快速提取特征点，然后通过BRIEF算法[13]（Binary Robust Independent Elementary Features）建立二进制描述符；该算法执行效率较高，但对抗视角变化和抗噪声能力较差。SIFT、SURF、ORB等算法的尺度空间均使用高斯滤波函数构建，而高斯滤波会致使图像边缘信息丢失，严重影响局部特征和描述符的稳定性。针对高斯滤波会造成尺度空间信息丢失等问题，提出了借助非线性扩散滤波构建尺度空间，如KAZE算法[14]，先通过AOS算法[15]解非线性方程构建尺度空间，然后利用M-SURF算法[10]构建描述符，KAZE算法的稳定性优于SURF算法，但是AOS算法迭代计算非线性方程耗时长。故在KAZE算法的基础上提出了AKAZE算法[16]（Accrlerated KAZE），该算法借助FED算法（Fast Explicit Diffusion）更高效的解非线性方程，然后利用MLDB算法[17]（Modified Local Difference Binary）构建二进制描述符。韩宇等人[18]提出一种基于改进SIFT算法的无人机航拍图像匹配算法，将SIFT算法矩形特征采样区域改成圆形，然后对描述符降维，最后借余弦距离衡量不同描述符的相似性。韩敏等人[19]提出一种改进KAZE算法无人机航拍图像匹配算法，使用二进制描述符替换KAZE算法的浮点型描述符，有效地加速了匹配算法。

高斯滤波构建尺度空间速度较快，但会造成图像边缘信息丢失，影响匹配算法的鲁棒性；非线性尺度空间虽更好地保护图像边缘信息，但是迭代计算非线性方程耗时较长。

针对上述问题，本文提出一种基于高斯曲率滤波[20]的局部特征匹配算法。首先使用高斯曲率滤波构建尺度空间，然后使用FAST算法提取特征点，其次对特征采样区域再次建立层度空间并在尺度空间中提取LIOP描述符[21]（Local Intensity Order Pattern），再对二阶尺度空间提取的LIOP描述符两两做差，最后设定阈值二值化差值LIOP描述符并累加得到稳定性更强的ASVLIOP描述符（Accumulated Stability Voting Local Intensity Order Pattern）[22]完成匹配。

1 算法理论

1.1 高斯曲率滤波

图像I(x)可以看做三维曲面(x,I(x))，则二维图像转化为三维曲面后可直接使用经典的微分几何处理三维曲面[19]。由经典的微分几何可知，可展曲面S的局部能够用其切平面TS(x0)近似，并且满足关系式：

二维图像中的高斯曲率为两个主曲率的乘积，由式（1）可知，任何可展曲面上任一点的高斯曲率均为零。因此，最小化其中任意一个主曲率，就相当于最小化高斯曲率。假设图像三维曲面(x,I(x))任意一像素点可表示为P(x0,y0,u0)，枚举其领域N((x0,y0,u0),δ)内所有的切平面为TSk(x0)，k=1,2,…,N，计算像素点P(x0,y0,u0)到切平面TSk(x0)的所有符号距离dk，k=1,2,…,N，其中最短距离对应的切平面TSk(x0)min可近似为三维曲面S。将点P与符号距离dm做加法运算，即将点P移动至TSk(x0)min便可完成一次图像的局部高斯曲率优化。

在图像域Ω内，以像素点U(i,j)为中心3×3领域，作为S(x,y)域，为了解除相邻图像之间的依赖性将S(x,y)内的像素划分为4类，保证U(i,j)在水平和竖直方向的同类像素均不相邻。

为了在域S(x,y)找到最小投影距离dmin，在域S(x,y)可分为三种类型的三角构型切平面，如图1所示。图1为三种三角构型切平面又各有四种可能切平面，共计12种可能三角构型切平面，其中部分三角构型切平面会有两顶点共线，故只需要计算其中8个切平面到像素点U(i,j)的距离。

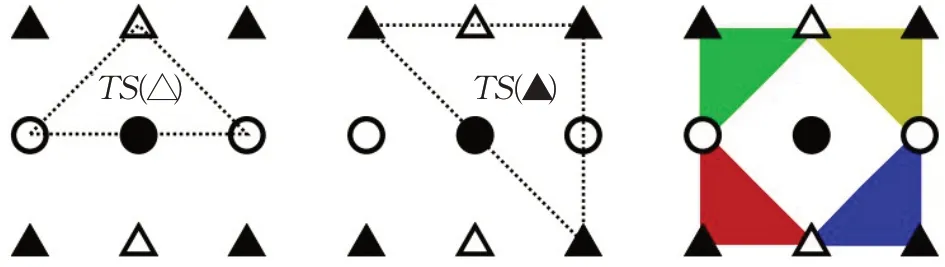
图1 构成切面的种类Fig.1 Types of section

三维曲面(x,I(x))到图2所示的8个三角构型切平面的投影距离dk,k∈1,2,…,8。计算三维曲面(x,I(x))到8个三角构型切平面的距离，再从中选择最小距离dmin，最后根据最小距离更新U(x,y)，具体步骤如下：

更新U(x,y)操作

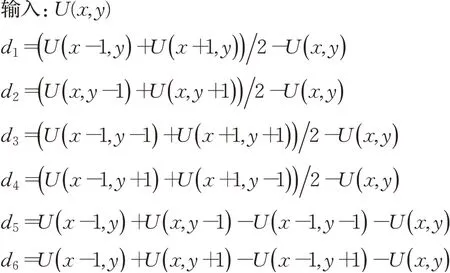
上述仅对一类三角构型平面操作，对其他三类投影操作则可完成高斯曲率滤波，具体如下：

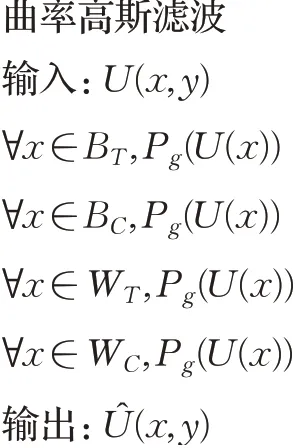
1.2 LIOP描述符建立

无论是SIFT算法的浮点型描述符还是ORB算法的二进制描述符，均需要建立特征描述符主方向，而由于匹配图像质量不同会导致同一特征区域主方向存在偏差，降低匹配算法的鲁棒性。本文所用LIOP描述符，根据特征采样区域内像素强度建立描述符，不需要建立描述符的主方向，故对亮度较差匹配图像鲁棒性较强。构建LIOP描述符步骤如下：

步骤1对特征采样区域P(x)中的像素点按大小顺序排列，并把排列结果映射到相应的排列序号，具体过程如下：

式中π=(i1,i2,…,iN)，P={xk1,xk2,…,xkN}为P(x)中像素点按大小顺序排列结果。

步骤2以采样点数量N，建立像素值强度排列顺序索引表，当N=4建立的强度排列顺序索引表，π为索引值。

步骤3以γ(P)=π映射的索引值编码N！的向量，可表示为：

式中Ind(π)表示索引值π在索引表对应的索引，向量φ(π)第Ind(π)=1，其余值均为0。

步骤4特征区域中单个像素点的的LIOP描述符建立方式如下式：

对同一个子区域的像素点的LIOP的描述符相加，得到该子区域的描述符，把所有子区域的描述串联便得到整个特征区域的描述符，表示方式如下：

式中，B表示为特征区域分为子区域的个数，则特征区域的描述符的维数为N!×B。

1.3 Accumulated Stability Voting算法

现在的特征匹配算法，均在不同尺度下提取特征点和描述符，为了增加描述符鲁棒性，提出ASV模型。具体步骤如下：

步骤1建立尺度空间，并在尺度空间中提取特征点，对于任何一尺度空间层，通过不同的尺度因子λ建立ns层尺度空间，新建的尺度空间为(λsσ,λlσ)，λs为新建尺度空间层的最小尺度因子，λl为新建尺度空间层的最大尺度因子。

步骤2特征点所在尺度空间，得到ns层尺度空间皆提取描述符，并计算不同层描述符的差值绝对值，用公式可表示为：

式（6）可判断描述符在不同尺度下的稳定性，式中xi、xj为j和i层尺度空间中提取的描述符，i、j的关系为1≤i,j≤ns，j≠i。例如，SIFT算法的描述符为128，则新构建尺度层之间描述符差值绝对值可表示为：式中，k为描述符维数，SIFT算法的k∈{1,2,…,128}。

步骤3新建尺度空间共有ns层，则不同层两两做差值共有个结果，若重新定义Vi,j为Vm，m∈[1,2,…,M]。为Vm设定阈值，将不同尺度描述符差值作稳定性量化，可表示：

式中，θt为阈值函数，tm表示为阈值。若则表示描述符第d维较为稳定，否则不稳定。在设置适当的阈值条件下，量化后的数据对噪声具有更强的鲁棒性。二进制稳定性值可以看做稳定性投票的过程，累积所有尺度对的二进制形式的稳定性hm，得到度量稳定性的整数型描述符表示为：

C反映了描述符的每一维在不同尺度下的鲁棒性。

2 算法实现

2.1 高斯曲率尺度空间构建

为了使局部特征匹配算法具有尺度不变性，特征提取和描述符构建均需在尺度空间中完成。在1.1节中，高斯曲率滤波是一个迭代优化的过程，每次迭代计算dmin，再通过Û(x,y)=U(x,y)+dmin迭代，可得到类似高斯滤波不同尺度因子λ的尺度空间。为了使匹配算法具有较好的尺度不变性和较高的运行效率，本文设置5层尺度空间，每一层的降采样率和高斯曲率迭代次数，如表1所示。

表1 尺度空间构建方式Table 1 Construction of scale space

图3 （a）为高斯滤波逐渐增加尺度因子滤波图像，随尺度因子增加图像边缘越来越模糊，图像信息丢失严重；图3（b）为逐渐增加高斯曲率滤波迭代次数得到滤波图像，滤波后图像保变性较好，信息丢失较少。

图3 高斯滤波与高斯曲率滤波效果对比Fig.3 Comparison of Gaussian filter and Gaussian curvature filter

2.2 描述符提取

在高斯曲率滤波金字塔上，利用FAST算法快速提取特征点，并以特征点为中心选择合适的区域作为特征采样区域。在1.2节中提出了局部强度顺序算法构建描述符，LIOP描述符根据特征采样区域内像素强度排列建立描述符，本身具有方向不变性，故不需要建立描述符的主方向。

电力巡线无人机拍摄的输电线路图像的复杂度较高，为了进一步提高匹配算法的鲁棒性，本文提出ASVLIOP描述符。1.3节中，高斯滤波函数构建金字塔后，再对金字塔每一层使用不同大小的尺度因子λ，重新构建ns层尺度空间；本文提出使用高斯曲率滤波构建尺度空间，通过改变图像U(i,j)迭代次数，可得到不同尺度层。在本文中，新建尺度空间层数ns取5，具体ASVLIOP描述符构建步骤如下：

步骤1尺度空间每层继续对U(i,j)迭代，尺度空间不同层ns对应的迭代次数分别为2、4、6、8、10。

步骤2对ns层尺度空间上的LIOP描述符，不同层求差值绝对值，可表示为：

式中，1≤i,j≤5，j≠i。LIOP描述符的维数为144维，则不同描述符做差值绝对值，可表示为：

式中，k为描述符维数，k∈{1,2,…,144}。

步骤3新建的尺度空间层数为5，则两两求差的绝对值得到10个矢量，对于对Vm设定不同的阈值，可得到：

式中，θt为阈值函数；tm表示为阈值，取值为5；d表示LIOP描述符的维数。

步骤4累积所有尺度对的二进制形式的稳定性hm，得到ASV_LIOP描述符，可表示为：

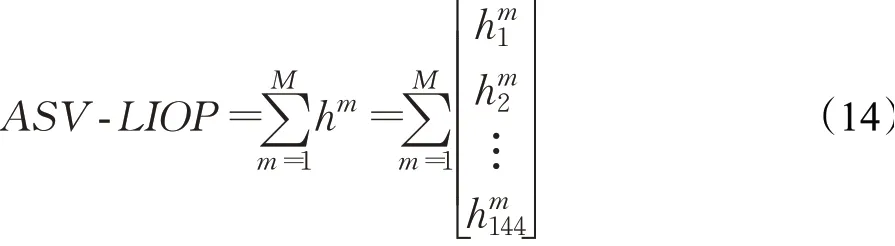
得到的ASV-LIOP描述符为整数型，使用欧式距离衡量不同描述符的相似性，并借助KD树算法搜索相似描述符。

3 实验

为了证明所提的基于局部特征的输电线路匹配算法的优越性，选择使用SIFT算法、ORB算法、KAZE算法和AKAZE算法、改进KAZE算法与所提算法在图4上对匹配算法的抗模糊变化、光照鲁棒性、尺度不变性、旋转不变性等特性测试。图4（a）和4（b）是两组待匹配原图像，对图像高斯滤波可模拟图像模糊变化；改变图像亮度可模拟光照变化对图像的影响；对航拍图像截取不同尺寸的图像可模拟图像尺度变化；对图像加上旋转角可模拟电力巡线无人机拍摄角度变化。

图4 实验图像Fig.4 Experimental images

为了更好地判断不同算法的鲁棒性，本文通过计算匹配图像正确匹配点数n与匹配点数N的比值，得到匹配算法的正确匹配率，如式（15）所示：

算法的运行时间反映了算法的匹配效率，本文通过计算每个特征匹配平均时间衡量，若两幅图像匹配耗时为Time，匹配点数为Num，则可得平均时间point_time可表示为：

本文使用Matlab2014a作为实验软件平台，并使用Opencv3.0数字图像处理库，计算机硬件配置为：Intel®i7-7700@2.6 GHz、内存8 GB。

3.1 抗模糊变化实验

电力巡线无人机在高空中拍摄输电线路时，可能会有雾霾、噪声等影响图像质量，降低了图像的清晰度，对图像4（a）高斯模糊处理以衡量算法的抗模糊变化能力。如图5所示，把图像分别分为5组，随着图像序号增加高斯模糊半径递增，图像的模糊程度增加。

图6 为SIFT算法、ORB算法、KAZE算法、AKAZE算法、改进KAZE和本文所提算法在图5上实验得到匹配正确率，由条形图可看出，随着图像模糊程度增加匹配正确率逐渐减小。由条形图可看出，ORB算法的匹配正确率最低且下降速度最快，本文算法匹配正确率与AKAZE算法差别不大；当图像模糊程度最高时，本文算法匹配正确率比AKAZE算法高8%左右。

图5 模糊变化图Fig.5 Fuzzy change diagram

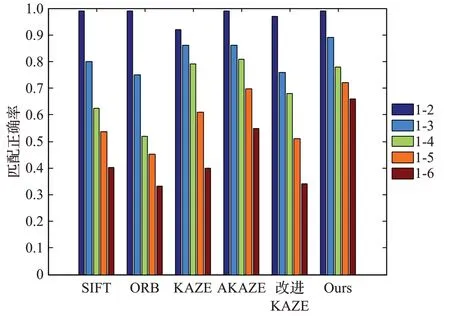
图6 模糊变化图像匹配正确率Fig.6 Image matching accuracy of fuzzy variation

表2 为图5（a）匹配点数和单点匹配时间，随着图像模糊程度的增加，每一种算法的匹配点数都在减少。由表2可知，SIFT算法得到匹配点数最多，其次是ORB算法，但这两种算法的匹配正确率均比较低，鲁棒性较差。ORB算法尺度空间和描述符构建比较简单，二进制描述符匹配速度较快，故ORB算法单点匹配速度最快。KAZE算法需要迭代计算解非线性方程，而且使用64维浮点型描述符，故匹配速度较慢。改进KAZE算法使用FREAK二进制描述符[23]代替SURF浮点型描述符，增加算法的匹配效率但降低稳定性，故改进KAZE算法单点匹配速度优于KAZE算法，匹配正确率不及KAZE算法。SIFT算法描述符为128维浮点型，利用欧式距离衡量不同描述符的相似性耗时较长，故效率不佳。本文提出的高斯曲率尺度空间构建速度较快，但需要二次构建尺度层，多次建立LIOP描述符，ASV-LIOP描述符整型，需要使用欧式距离衡量不同描述符的相似度，故匹配速度最慢。如表2所示，在具有模糊变化图像匹配中，ORB算法单点匹配速度最快，其次是AKAZE算法，本文所提算法匹配速度最慢。

表2 模糊变化图像对比结果Table 2 Comparison of fuzzy change images

3.2 光照鲁棒性实验

为了模拟天气变幻、拍摄阴影或者时间不同，对电力巡线无人机航拍图像亮度造成的影响，对图4（b）的亮度依次下降，变化幅度为10，变化范围从0到−50。如图7所示，随着图像序号的增加，图像亮度依次下降。

图7 光照变化匹配图像Fig.7 Illumination change matching image

图8 柱状图为各种算法在图7得到的匹配正确率，由柱状图可看出，随着图像亮度的增加各种算法的匹配正确率逐渐下降，其中ORB算法下降速度最快，AKAZE算法次之。本文所提算法在亮度差最大时，匹配正确率仍高于60%，且随着亮度下降，所提算法的下降速率不超过10%。

图8 光照变化图像匹配正确率Fig.8 Image matching accuracy of illumination change

SIFT算法、ORB算法、KAZE算法、AKAZE算法和改进KAZE算法均需建立特征采样区域主方向，然后把描述符旋转至主方向位置，才可进行特征匹配，但是当光照条件较差时，特征采样区域的梯度较小，建立的主方向不具有较好的区分性，会导致匹配算法的精度下降。所提ASV-LIOP算法先对特征采样区域像素按照强度排序，然后建立索引表编码得到LIOP描述符，最后在多种尺度下建立ASV-LIOP描述符，该描述符对光照变化敏感度较低，与SIFT、AKAZE等算法相比，光照鲁棒性最强。表3中，本文所提算法匹配点数相比SIFT算法、ORB算法和AKAZE算法较少，但是匹配正确率越超过这几种算法。所提算法的描述符构建过程较为复杂，故单点匹配耗时最长，如表3所示。

表3 光照变化图像对比结果Table 3 Comparison result of illumination changes

3.3 尺度变化实验

为了模拟电力巡线无人机飞行高度的变化造成相邻输电线路图像的尺度不同，对图4（a）图像乘不同的尺度系数，然后在中心点位置截取比例图像，如图9所示。

图9 尺度变化匹配图像Fig.9 Scale change matching image

尺度变化图像匹配正确率如图10所示，ORB算法、SIFT算法、KAZE算法、AKAZE算法、改进KAZE算法和本文算法的特征提取和描述符建立均在尺度空间中，以上几种算法具有较好的尺度不变性。所提算法的匹配正确率与AKAZE算法、KAZE算法相差不到5%，相较ORB算法提高了15%左右。

图10 尺度变化图像正确匹配率Fig.10 Correct matching rate of scale change images

表4 为上述算法在尺度变化图像上的匹配点数和单点匹配时间，由表4知，SIFT算法的匹配点数最多，ORB算法其次，KAZE算法匹配点数最少。ORB算法匹配点数虽多，但是匹配正确率较低，故鲁棒性较差。所提算法的匹配点数相较SIFT算法少，但是匹配正确率远超过SIFT算法。所提算法的匹配正确率与KAZE算法、AKAZE算法相差较小，但匹配点数远超过KAZE和AKAZE算法。所提算法单点匹配耗时最长，约为8.1 ms。

表4 尺度变化图像对比结果Table 4 Comparison of images with scale change

3.4 旋转不变性实验

为了模拟电力巡线无人机在高空中航向或者云台角度的变化，对图4（b）顺时针依次旋转15°得到旋转图像，然后以中心点截取部分图像，得到图11。

图11 角度变化部分匹配图像Fig.11 Angle change of partial matching image

ORB算法、SIFT算法、KAZE算法、AKAZE算法和改进KAZE算法为了满足旋转不变性，均需要为描述符建立主方向，而相同特征采样区域建立的主方向可能具有差异，会造成同一特征描述符的距离增加，误判为错误匹配点。所提ASV-LIOP描述符，不需要建立特征采样区域主方向，本身具有旋转不变性，故对具有旋转图像的匹配效果较好，故匹配正确率最高，如柱状图12。

图12 角度变化图像正确匹配率Fig.12 Correct matching rate of angle change images

表5 统计了旋转图像匹配点数和单点匹配时间，SIFT算法匹配点数最多，ORB算法次之，KAZE算法匹配点数最少。对于旋转变化图像，ORB算法匹配点数虽多，但匹配正确率最低；所提算法匹配点数相较ORB算法少，但是匹配正确率高于ORB算法7%左右。

表5 角度变化图像对比结果Table 5 Comparison of angle change images

4 结束语

本文提出一种基于高斯曲率滤波的电力巡线无人机航拍图像匹配方法，首先使用保边性更好高斯曲率滤波算法构建金字塔，然后用FAST算法检测特征点，再对金字塔二次建立尺度空间并提取每层尺度空间内特征点的LIOP描述符，随后对不同尺度层上LIOP描述符两两做差，再设置阈值二值化差值LIOP，最后累加得到ASV-LIOP描述符。实验表明：本文算法的稳定性比传统算法更强，可获得较多的正确匹配点。在进一步的工作中，在不影响算法的鲁棒性前提下，进一步提高算法的匹配效率。