有源配电网中智能储能软开关规划
2021-11-12王春义丁子甲张兴友何召慧徐振东
王春义,丁子甲,张兴友,何召慧,徐振东
(1.国网山东省电力公司,山东 济南 250001;2.国网山东省电力公司济宁供电公司,山东 济宁 272100;3.国网山东省电力公司电力科学研究院,山东 济南 250003;4.山东科技大学电气与自动化工程学院,山东 青岛 266590)
0 引言
随着大量分布式电源(Distributed Generation,DG)接入配电系统,传统配电网已经难以满足高新能源渗透率的要求,大量新能源接入系统在提升可再生能源利用率以及系统经济性的同时,会对配电网的可靠性和稳定性带来很大的挑战。目前配电网的调控手段主要通过调节开关状态来改变网架拓扑,以实现负荷的转供、降低网络损耗[1]。近年来,电力电子技术的大力发展推动了柔性电力电子设备的不断革新,智能软开关(Soft Open Point,SOP)在这种背景下衍生。作为一种智能配电装置,智能软开关具有双向调节系统潮流的能力[2],既可以提升DG的渗透率,减缓网络堵塞,同时可以对馈线的无功功率进行调节,以改善电压水平,提高系统稳定性。智能软开关实现了馈线之间的柔性互联[3],可以实现实时的优化,在空间和时间两个维度对系统进行调节。
目前国内外对于智能软开关的研究已有初步成果,文献[4]研究系统接入智能软开关的成本及运行成本,同时考虑联络开关和智能软开关,提出它们同时存在的时序优化模型,并利用模拟退火法和锥规划结合的混合算法进行优化。文献[5-6]考虑到不同主体的利益需求,通过对分布式电源和智能软开关的多层协调优化来协调DG 运营商与配电公司的利益。文献[7]考虑系统的不确定性因素,提出了两个灵活性指标,构建了以灵活性和经济性综合性能为目标的模型。文献[8]兼顾系统运行经济性及可靠性指标,通过可靠性与经济性的协调规划有效降低了配电网综合成本,提升了经济效益。文献[9]利用场景生成法构建典型场景,构建了智能软开关选址定容的双层规划模型。文献[10]为提升配电网运行经济性,利用改进灵敏度分析方法对SOP 选址定容。
储能装置通过存储或者释放电能,可以在时间维度实现上对电能的转移,以平衡分布式电源的波动性和间歇性,提高DG的消纳水平[11]。基于储能装置的这一优点,智能储能软开关(Soft Open Point Integrated With ESS,ESOP)应运而生。智能储能软开关通过SOP 与ESS 的高度集成,从时间和空间两个维度调节系统潮流分布,从而降低网损、提高电压水平。文献[12-13]介绍了ESOP的物理结构和数学模型,构建了有源配电网中ESOP 的时序优化模型。由于大功率电力电子装置的投资成本比较高,因此选择合理的规划方案对有源配电网经济性的提升有着重大意义。
在上述背景下,为进一步提升配电网调节性能的灵活性与运行经济性,考虑DG 和负荷的时序特性,以配电网络年度综合成本最小为目标建立了有源配电网中ESOP 规划模型。最后,利用IEEE33 节点算例验证模型的有效性和可行性。
1 数学模型
1.1 智能储能软开关
受客观因素限制,一般将ESOP安装在联络开关或分段开关处。以背靠背电压源型换流器为例,其物理拓扑结构如图1 所示。图中,ESS 为储能电池,SOP 为智能软开关,储能电池可以通过直流环节耦合到SOP,通过换流器实现电能的吸收或释放。
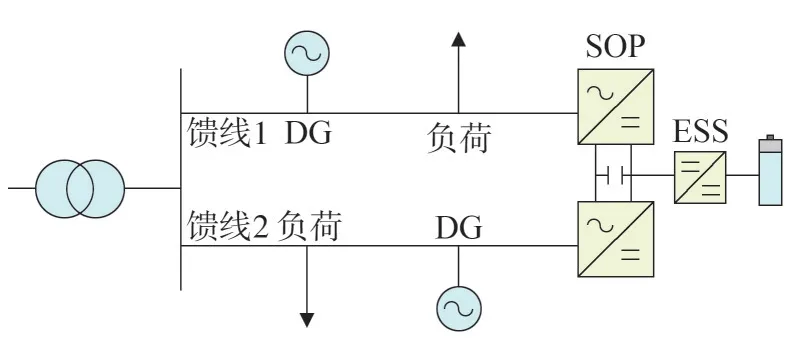
图1 ESOP在配电网中的接入位置
与SOP 相比,ESOP 的数学模型变得更加复杂,其中SOP部分的相关运行约束条件为:
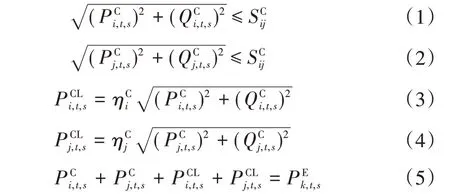
由于智能储能软开关中SOP 装置和ESS 装置的高度集成与耦合,因此还要考虑储能系统的运行约束,其相关约束条件为:
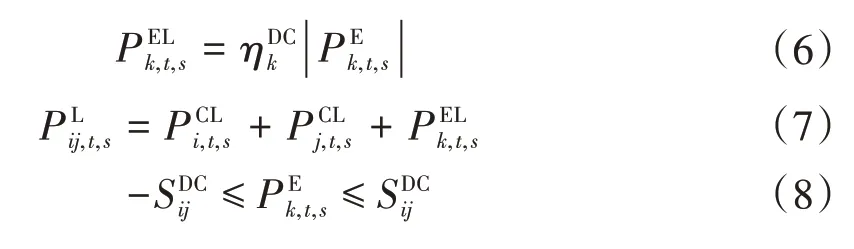
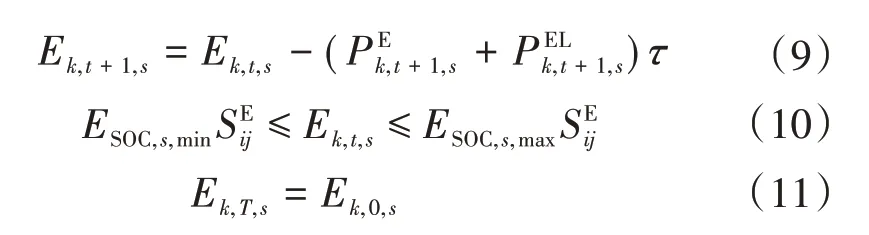
1.2 光伏发电模型
DG 并网对于降低网络损耗、提高电压质量以及减少环境污染有着重要作用,但以风电和光伏为主的间歇性DG具有波动性和不确定性的特点,因此充分考虑其时序性模具有重要意义。
通常用Beta 分布来描述光照强度[14],其概率密度函数为
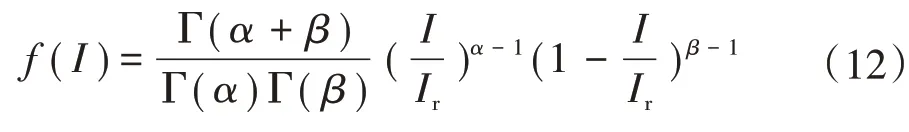
式中:I为光照强度;Ir为最大光照强度;α、β为形状参数。
光伏的功率可以由光照强度表示为
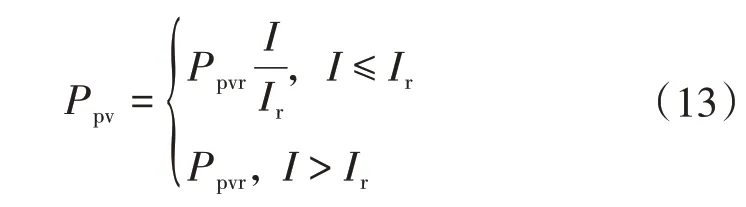
式中:Ppv为光伏实际出力;Ppvr为光伏出力的额定值。
1.3 风力发电模型
一般用两参数的Weibull 分布来描述风速[15],其概率密度函数为
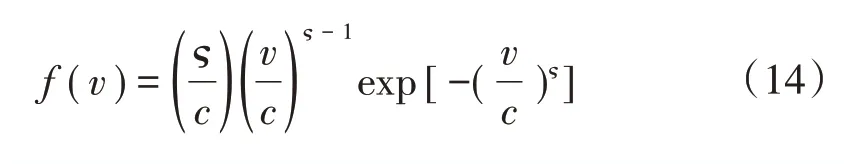
式中:v为风速;c和ς分别为尺度参数和形状参数。
风电的实际出力可以通过风速近似地表示为
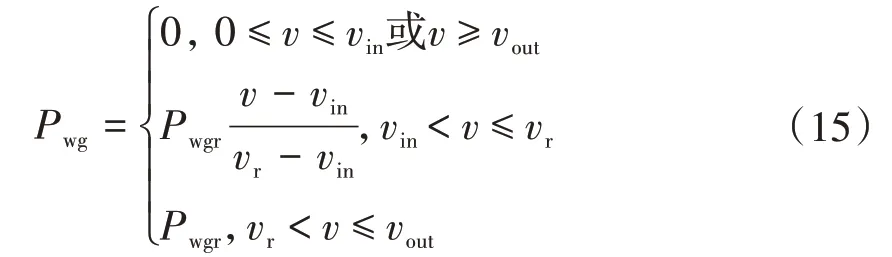
式中:Pwg为风力发电机的实际出力;Pwgr为额定功率;vin、vr、vout分别为切入风速、额定风速和切出风速。光伏和风电的典型出力时序曲线分别如图2 和图3所示[16]。
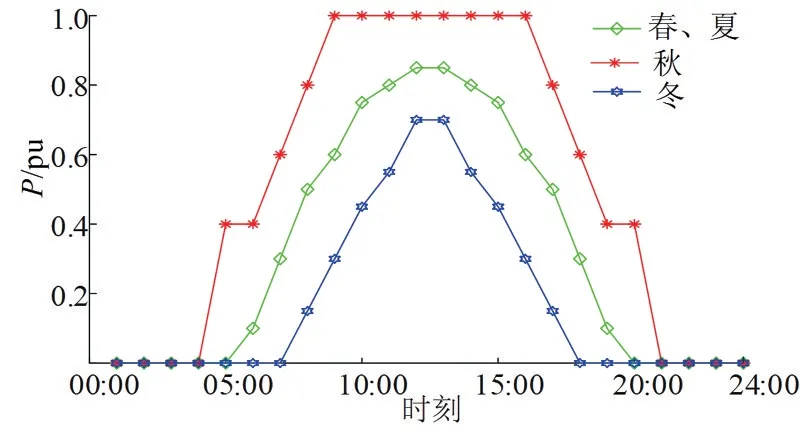
图2 光伏典型出力曲线

图3 风电典型出力曲线
1.4 负荷
一般情况下,负荷满足正态分布[17],其概率密度函数为
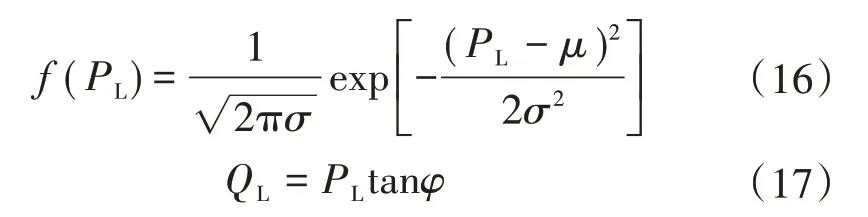
式中:PL为负荷有功功率;QL为负荷无功功率;μ为有功期望值;σ为有功标准差;φ为功率因数角。
考虑居民、工业和商业3 种负荷类型,3 种负荷类型的典型出力曲线[16]分别如图4—图6所示。
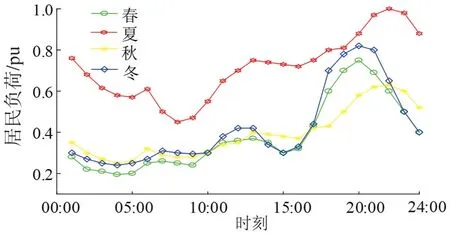
图4 居民负荷四季典型出力曲线
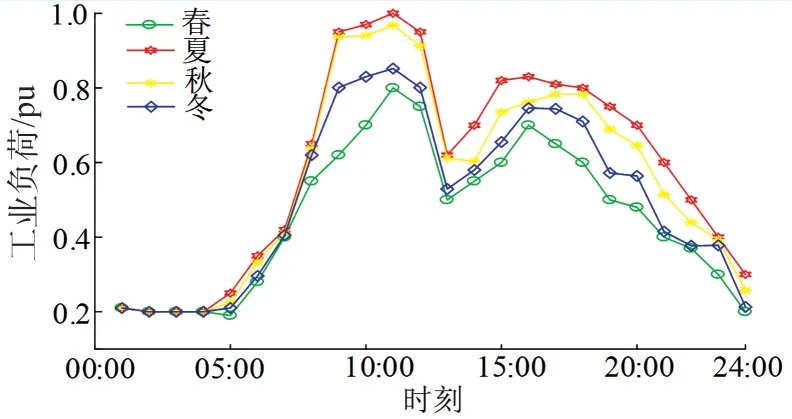
图5 工业负荷四季典型出力曲线
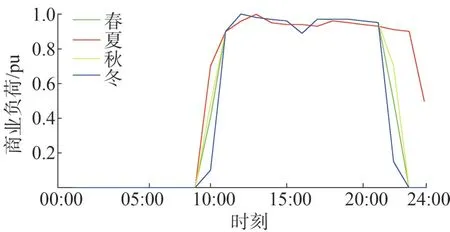
图6 商业负荷四季典型出力曲线
2 目标函数
对年度智能储能软开关投资成本、运行维护成本以及系统损耗成本进行综合考虑,以年度综合成本作为目标函数,具体表达如式(18)—式(21)所示。
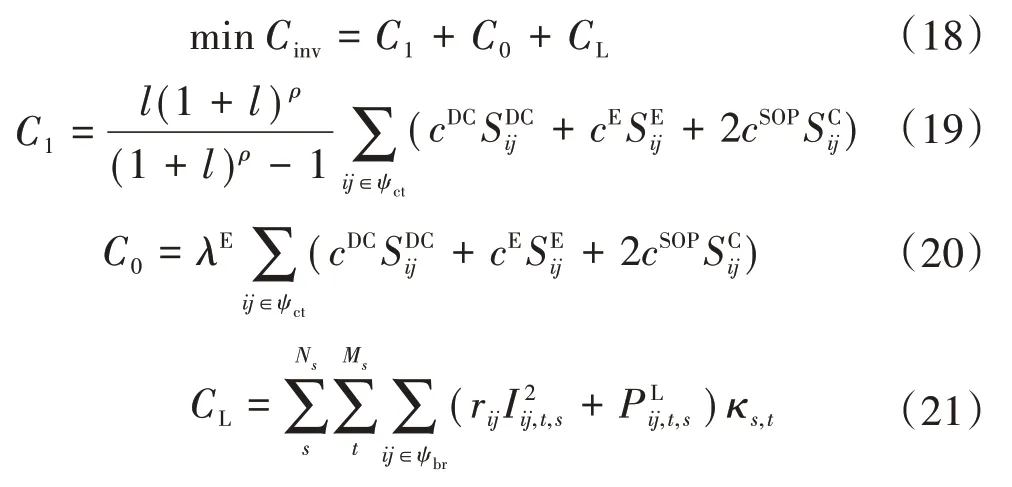
式中:Cinv为年度综合费用;C1为年度投资成本;C0为运行维护成本;CL为年网损成本;l为贴现率;ρ为设备经济使用年限;ψct为联络开关集合;cDC、cE和cSOP分别为DC/DC 转换器、储能电池和换流器的单位容量投资成本;λE为运行维护成本系数;Ns为场景数;Ms为场景s在一年中的总时长;ψbr为所有支路集合;rij为支路ij的电阻值;Iij,t,s为场景s下t时刻支路ij的电流大小;κs,t为场景s下t时刻的电价。
3 约束条件
1)智能储能软开关运行约束。具体表达式见式(1)—式(11)。
2)潮流约束。系统要满足潮流平衡约束,采用distflow 支路潮流法[18],具体如式(22)—式(27)所示。
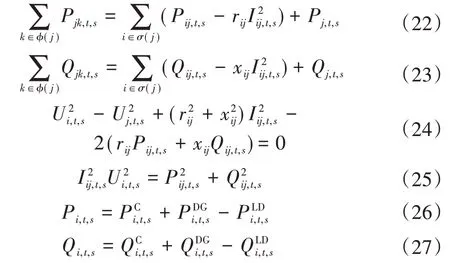
式中:φ(j)、σ(j)分别为以j为首节点和末节点的节点集合;Pij,t,s、Qij,t,s分别为场景s下t时刻支路ij的有功功率和无功功率;Pi,t,s、Qi,t,s分别为场景s下t时刻注入节点i的有功和无功功率;Ui,t,s、Uj,t,s分别为场景s下t时刻节点i、节点j的电压;xij为支路ij的电抗值;分别为场景s下t时刻DG 注入节点i的有功功率和无功功率;分别为场景s下t时刻节点i处负荷的有功功率和无功功率。
3)分布式电源输出功率约束为:
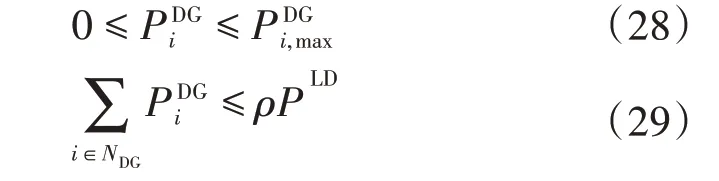
4)系统运行约束。系统在运行时,电压和电流值应保持在安全范围内。系统安全约束为:
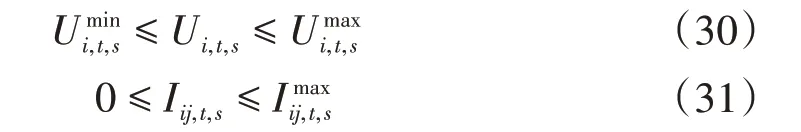
5)智能储能软开关规划约束为:
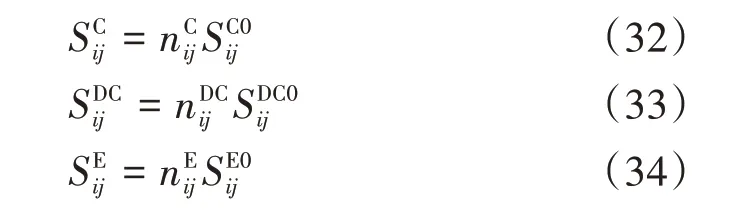
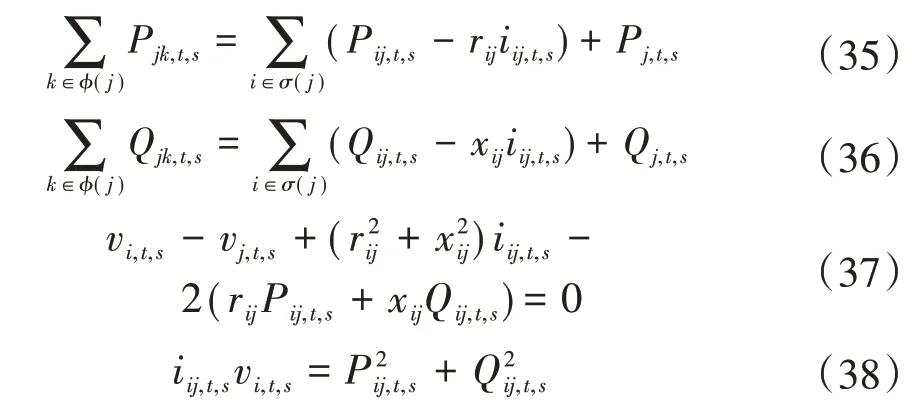
ESOP 的运行约束式(3)、式(4)以及潮流约束式(38)中存在二次项,对其进行凸松弛处理[19-20]。
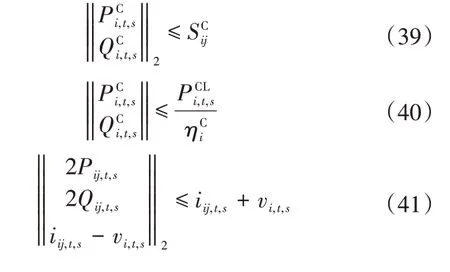
4 算例分析
采用改进的IEEE33 节点算例对配电网中智能储能软开关的规划进行分析与验证,其拓扑结构如图7 所示。其中节点1 为电源节点,电压等级为12.66 kV,基准功率为1 MVA;负荷总的有功功率为3 715 kW,无功功率为2 300 kVar。负荷和DG 的时序数据来源于文献[16],ESOP 的经济性能参数取自文献[21]。红线表示联络开关支路,将ESOP安装在联络开关上。在节点10、16、17、30、33 安装WG,额定容量为300 kVA,功率因数为1;在节点7、13、27安装PV,额定容量为200 kVA,功率因数为1;硬件环境为AMD Ryzen3 2200U CPU,主频2.50 GHz,内存8.0 GB,开发环境Win10 64 位,仿真软件为MATLAB2016b,采用YALMIP 求解器和CPLEX 算法包进行求解。
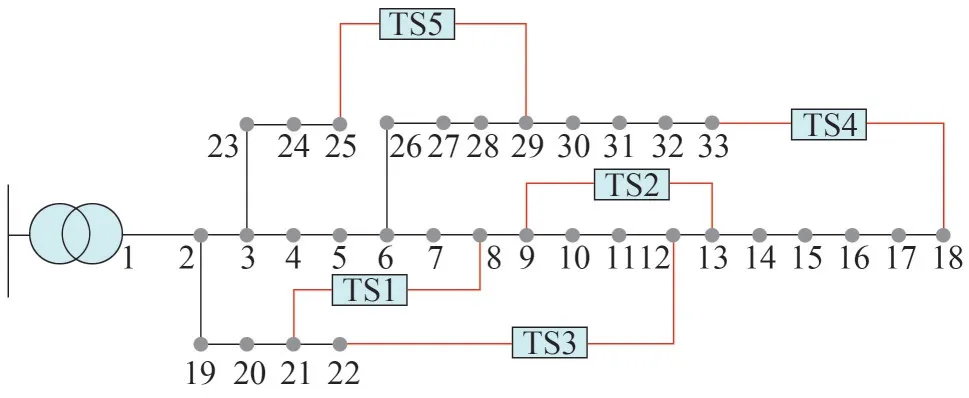
图7 改进IEEE33节点算例
考虑到负荷的时序特性,采用分时电价的方式,根据负荷的峰谷水平设置不同的购电价格,分时电价参数如表1所示。

表1 分时电价参数
根据本文方法对智能储能软开关进行规划,规划结果换流器容量、DC/DC 转换器容量以及储能电池容量如表2所示。
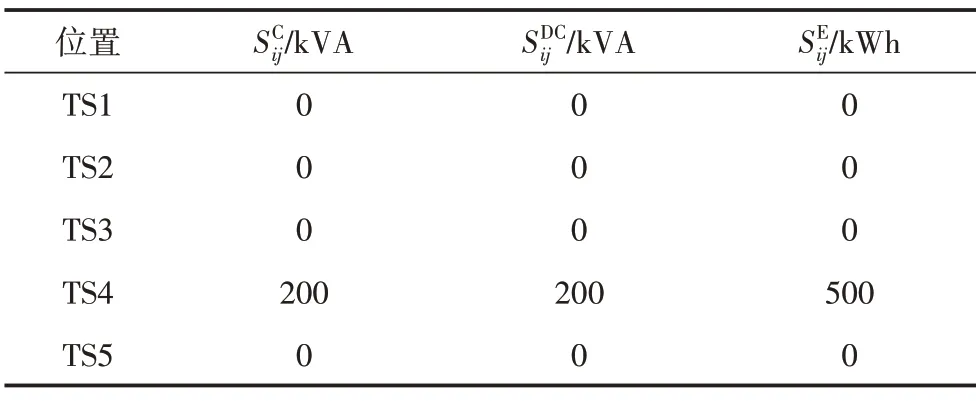
表2 ESOP规划结果
为了验证所提出的配电网中合理的ESOP 规划方案对系统经济性的提升效果,从ESOP的安装容量和安装位置两个方面进行分析。
为分析ESOP 中ESS 及换流器的安装容量对系统经济性的影响,在本文的规划结果的基础上,设置2 种随机情形进行对比分析。各情形的ESOP 配置情况见表3。各项成本如表4 所示,其中情形3 取表2中的规划结果。

表3 3种情形的ESOP配置情况
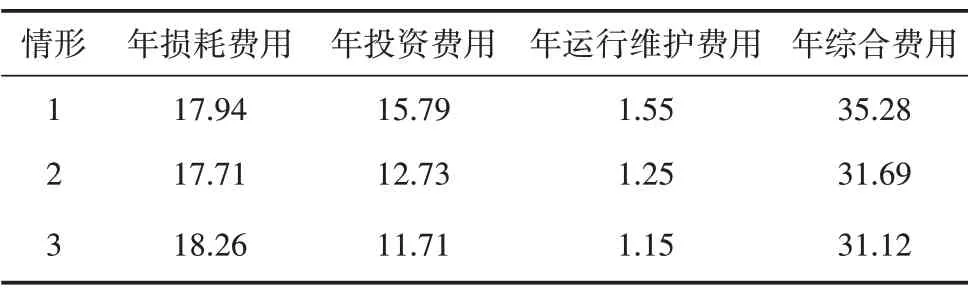
表4 3种情形的各项成本 单位:万元
由表4 可以看出,3 种情形的年综合成本呈现下降趋势。相比于情形3,情形1 增加了换流器容量,换流器损耗增大,但是换流器增加的容量使ESOP对两端馈线的功率调节作用增强。情形2 增加了DC/DC 转换器容量以及储能电池容量,储能部分的损耗增大,由于储能装置具有可转移电能、削峰填谷的作用,配置了储能装置的智能软开关可以实现与较大容量智能软开关相同的降损效果,因此情形2 的年损耗费用最低。储能装置与换流器相比,投资费用较低,因此情形2 的年综合费用明显低于情形1。情形1和情形2的年损耗费用降低,但接入容量增大导致投资费用和运行维护费用增加。统筹考虑各项成本,情形3的年度总成本最低。
与上述对比方法类似,设置另外3 种情形比较ESOP 不同安装位置对系统经济性的影响。为与本文规划方法形成对比,3 种情形的ESS 与SOP 安装总容量相等,3 种情形的配置情况和成本分别如表5 和表6所示。

表5 3种情形的ESOP配置情况
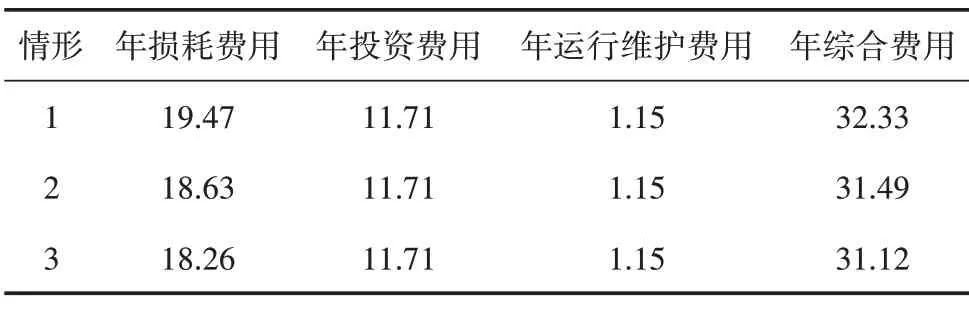
表6 3种情形的各项成本 单位:万元
由表6 可以看出,ESOP 安装在不同的位置对系统的优化作用不同。3 种情形的年投资和运行维护费用相等。TS4 处于馈线末端,负荷需求较大,有利于发挥SOP 对功率的调节作用以及ESS 的电能转移作用。情形2 在TS3、TS4 处都安装了ESOP,SOP 容量分别安装了100 kVA,ESS 分别安装200 kWh 和300 kWh,年损耗费用低于情形1。情形3中ESOP只安装在TS4 处,有着最好的降损效果,因此情形3 的年度总成本最低。综上,根据系统实际运行情况对ESOP 的安装位置和安装容量合理规划对于提高系统运行经济性有着重要意义。
5 结语
智能储能软开关能从时间上和空间上对系统潮流进行优化,实现功率转移、削峰填谷的作用。本文考虑负荷和DG的时序特性,建立了年综合成本最小为目标函数的ESOP 规划模型,并通过IEEE33 节点算例系统对规划模型进行了验证与分析。结果表明,通过对配电网络中智能储能软开关的安装位置和安装容量进行合理的规划,能够有效提高系统运行的经济性。
