基于改进遗传算法的主动配电网经济优化调度

黄治翰，汪 晗，李启迪，刘 闯

（1.国网湖北省电力有限公司鄂州供电公司，湖北 鄂州 436000；2.国网湖北省电力有限公司荆门供电公司，湖北 荆门 448000）

0 引言

随着国家节能减排要求的提高，可再生能源的利用率越来越高［1-4］。风能、太阳能等可再生能源的开发虽然一定程度上缓解了能源需求，但其大规模并网也给电力系统安全性和稳定性造成了一定威胁，也给电网经济调度带来了巨大挑战［5-8］。主动配电网（Active Distribution Networks，ADN）技术的发展为可再生能源大规模并网提供了便利，但由于ADN中涉及发电、储能和用电等各项成本，其经济性不容忽视［9-12］，因此，为了提高可再生能源的消纳能力和降低ADN 系统的投资成本，有必要对ADN 经济优化调度展开研究。

文献［13］针对风电出力的不确定性，为了消除风功率预测误差对ADN经济调度的影响，采用worstbest理论对预测结果进行鲁棒优化处理，建立了相应的ADN 经济优化调度模型；文献［14］利用储能设备消除ADN 系统中风电波动性的影响，建立了包含风力发电与储能设备的ADN 优化调度模型，并采用改进萤火虫算法对模型进行求解，取得了不错的应用效果；文献［15］为了增加ADN 优化调度的经济性和安全性，在建立ADN 优化调度模型的过程中考虑了需求侧资源的影响，应用算例分析验证了模型的有效性；文献［16］为了降低环境成本和提高经济效益，提出了一种包含分布式电源、储能系统的ADN 日前有功优化调度模型，采用粒子群优化算法（Particle Swarm Optimization Algorithm，PSO）获得了最优解。上述研究虽然取得了一定研究成果，但由于ADN 优化调度目标函数和约束条件比较复杂，其模型和求解方法还有待进一步完善。

针对现有研究中存在的不足，对ADN 电网运行过程中产生的购电成本、运行维护成本、折旧成本、损耗成本、售电收益等各项成本进行分析，综合考虑各类约束条件，建立以总成本最小为目标函数的ADN 经济优化调度模型，并用改进遗传算法对模型进行求解，验证ADN 优化调度模型和求解方法的正确性。

1 ADN经济调度模型

ADN通常由“源”、“网”、“荷”3部分组成，“源”一般是指风电、光伏等可再生能源和微型燃气轮机等，“网”是指配电网系统中的网架结构及开关设备，如联络开关、支路开关等，“荷”是指用户负荷以及蓄电池储能、电容器储能和飞轮储能等储能系统［17］。图1给出了ADN 的结构简图，风推动风机转动将风机的机械能转化为电能接入电网，光伏通过吸收太阳光将太阳能转化为电能接入电网，微型燃气轮机通过做功发出电能接入电网，储能装置既可以作为电源为系统提供电能，也可以作为负荷消耗电能，用户负荷作为耗能者，从电网中吸收电能。当联络开关闭合时，两级配电网之间可进行电能交换。

图1 ADN结构简图

1.1 ADN优化调度目标函数

研究表明，ADN 在运行过程中产生的费用主要包括几个部分：1）ADN 系统中用电负荷大于发电负荷时，向上级系统购买电能产生的成本；2）ADN 系统中的发电设备（风机、光伏、燃气轮机、储能系统）在运行过程中所需的运行维护成本；3）风电机组、光伏设备、燃气轮机及储能系统的折旧成本；4）ADN 系统中的线路产生的网损成本；5）ADN 系统中的发电量大于用电负荷时，向上级系统出售电能产生的收益。

综合上述成本，充分考虑电能平衡和分布式能源运行等约束条件，建立以ADN 总成本最小为目标函数的ADN 优化调度模型，令调度周期为T，具体目标函数为

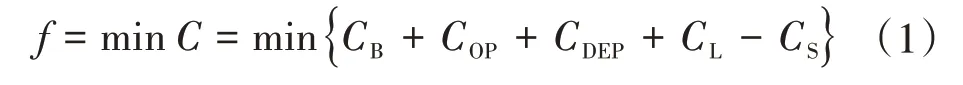
式中：C为ADN 总成本；CB为向上级系统购买电能产生的成本；COP为ADN 系统中的风机、光伏、燃气轮机和储能系统等设备在运行过程中所需的运行维护成本；CDEP为风电机组、光伏设备、燃气轮机及储能系统的折旧成本；CL为ADN 系统的损耗成本；CS为ADN系统出售电能产生的收益。

CB的计算公式为

式中：EB为ADN 系统在调度周期内的购电电价；PB为ADN系统在调度周期内的购电功率。

COP的计算公式为

式中：M为ADN 中发电系统的种类；ROP.i为第i类能源系统运行维护费用的比例常数；POP.i为调度周期内第i类能源系统的发电功率。

CDEP可采用固定资产折旧法进行计算，即根据运行年限对能源系统的购买成本进行折旧，计算公式为式中：l为能源系统的运行年限；CG.i为第i类能源系统的安装成本。

CL的计算公式为

式中：Ploss.j为第j条线路在调度周期内的有功损耗；z为ADN系统中的线路总数。

CS的计算公式为

式中：ES为ADN系统在调度周期内的售电电价；PS为ADN系统在调度周期内的售电功率。

1.2 约束条件

ADN 优化调度模型的约束条件可以从电能平衡约束、能源系统运行约束和储能系统约束等3个方面进行考虑。

1.2.1 电能平衡约束

由于ADN 系统中存在储能系统，这些储能系统既可以作为发电设备产生电能，也可以作为负荷消耗电能，因此电能平衡约束应分为储能系统充电和放电两种情况进行讨论。

1）储能系统充电下电能平衡约束为

式中：T为调度周期；Pw.T为调度周期内风力发电的总输出功率；Pp.T为调度周期内光伏发电的总输出功率；Pm.T为调度周期内燃气轮机的总输出功率；Pbt.T为调度周期内储能系统输出功率，当储能系统充电时Pbt.T＜0，当储能系统放电时Pbt.T＞0；ηch为储能系统的充电效率；Pld.T为调度周期内用户负荷功率；PL为调度周期内配网线路损耗功率。

2）储能系统放电下电能平衡约束为

式中：ηd为储能系统的放电效率。

1.2.2 能源系统运行约束

1）风电机组出力约束为式中：Pwα,T为调度周期内第α台风电机的输出功率；分别为第α台风电机最小输出功率和最大输出功率。

2）光伏设备出力约束为

式中，Ppβ，T为调度周期内第β台光伏设备的输出功率；分别为第β台光伏设备最小输出功率和最大输出功率。

3）燃气轮机出力约束为

式中：Pmλ,T为调度周期内第λ台燃气轮机的输出功率分别为第λ台燃气轮机最小输出功率和最大输出功率。

1.2.3 储能系统（蓄电池）约束

储能系统（蓄电池）约束为

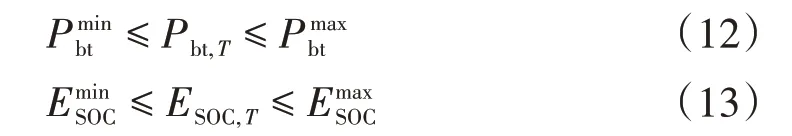
2 改进遗传算法求解ADN优化调度模型

2.1 改进遗传算法

遗传算法（Genetic Algorithm，GA）是一种模拟生物进化过程的寻优方法［18-19］。GA 算法在进化初期，随机给定的初始种群中可能存在少量适应度较好的个体，这些适应度值较好的个体可能会被重复选择，导致它们的子代中在进化后的种群中占据了主导地位，经过交叉和变异后，得到的后代仍与父本相同或相近，出现早熟现象，达不到理想的寻优效果。在进化后期，种群中个体的适应度值相对稳定，相互之间的多样性大大降低，导致算法收敛缓慢甚至不收敛。为了克服GA 算法的这些缺点，采用交叉、突变概率动态设定的方法对GA 算法进行改进。

1）交叉概率的改进。

首先设定交叉概率的最小值，然后随着迭代次数的增加，利用适应度值的标准差控制交叉概率的变化，使进化初期交叉概率较大，进化后期交叉概率较小。即交叉概率为

式中：pcmin为交叉概率的最小值；fi为个体i的适应度值；favg为种群中所有个体的平均适应度值；N为种群容量；pca为交叉概率调节参数。

2）突变概率的改进。

首先设定突变概率的最大值，然后随着迭代次数的增加，利用适应度值的标准差控制突变概率的变化，使进化初期突变概率较大，进化后期突变概率较小。即突变概率为

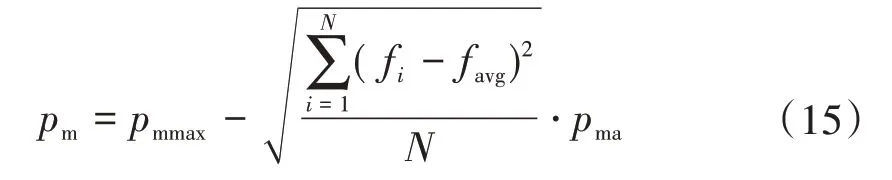
式中：pmmax为突变概率的最大值；pma为突变概率调节参数。

在进化初期，种群中个体适应度较差，个体之间差距不大，改进遗传算法通过增大交叉概率，使优秀个体能够尽快显示出来，缩小最优解的搜索范围；相反在进化后期，种群中个体适应度普遍较好，相互之间差异不大，改进遗传算法通过增大突变概率，增强种群局部搜索能力，快速找到最优解，加快算法收敛。

2.2 求解步骤

采用改进遗传算法对ADN 经济优化调度模型进行求解，具体求解步骤为：

1）根据需要设置ADN 的调度周期，本文将调度周期设置为24 h；

2）对ADN 系统的相关参数进行设置，包括风电机组、光伏设备、燃气轮机、储能系统（蓄电池）和电价信息等参数；

3）从调度部门获取风电出力、光伏出力及调度周期的用电负荷；

4）采用随机生成的方式获得改进GA 算法的初始种群，确定改进GA 算法的编码方式，设置种群规模为30，最大迭代次数为100；

5）对随机生成初始种群中的每个个体进行解码，根据公式（1）目标函数计算个体适应度值；

6）判断个体适应度值是否满足迭代终止条件，若已达到最大迭代次数，则解码获得适应度值的最优个体，否则，继续迭代；

7）根据公式（14）和公式（15）分别计算本次迭代的交叉概率pc和突变概率pm；

8）执行选择、交叉和突变等操作，产生新一代种群，返回步骤5）重新执行迭代；

9）当迭代后已获得适应度值的最优个体以及达到最大迭代次数时，输出目标函数最小值。

3 算例分析

选取标准的IEEE33 节点配电系统并配置有能源系统（风机、光伏、燃气轮机）和蓄电池储能系统构成的ADN 进行仿真分析。33 节点网络结构如图2所示，在图2中，源节点为0，即主电网节点，为了配电网系统的供电可靠性，在部分节点之间设有联络开关（图中虚线部分），各节点相关参数见文献［20］。其中，风电系统配置在节点9，额定容量为300 kW，光伏系统配置在节点15，额定容量为100 kW，统燃气轮机系统配置在节点20，额定容量为420 kW，蓄电池系统配置在节点9，额定容量为150 kW。

图2 33节点配电网系统

ADN 经济优化调度目标函数参数设置为：购电电价EB=0.55元/kWh，售电电价ES=0.4元/kWh，风电、光伏和燃气轮机等能源系统的设计寿命L为30 年，蓄电池储能系统设计寿命为10 年，其充、放电效率ηch、ηdi均为0.9。能源系统及储能系统的安装及维护成本如表1所示。

表1 能源系统及储能系统的安装及维护成本 单位：元/kVA

从调度部门获取调度日当天用电负荷、风电出力和光伏出力，具体如图3 所示。

图3 调度日负荷预测结果

采用改进遗传算法对ADN 系统总成本进行优化，其目标函数的变化曲线为图4 中的黑色线，ADN总成本在种群迭代45 次后找到最优解，最优解为193 860 元。为了对比说明改进GA 的优越性，采用遗传算法对目标函数进行优化，其迭代曲线为图4中的红色线，GA 需要92 次迭代才能找到最优解，最优解为200 448 元。对比二者寻优结果可以看出，改进GA 能够明显加快算法收敛，提高计目标函数解的计算精度。

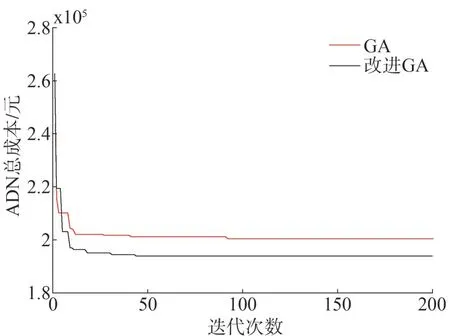
图4 GA与改进GA寻优迭代图

表2给出了利用改进GA 和GA 进行ADA 经济优化调度时的各项成本。从表2 可以看出，基于改进GA 的主动配电网经济优化调度模型的购电成本、运行维护成本、折旧成本、损耗成本相比GA 均有所降低，降幅分别为3.19%、3.34%、6.11%和7.28%，可见改进GA 在进行ADA 能够节约更多的成本。在售电收益上，改进GA 方法获得的售电收益比PSO 增加了9.31%，经济性更好。

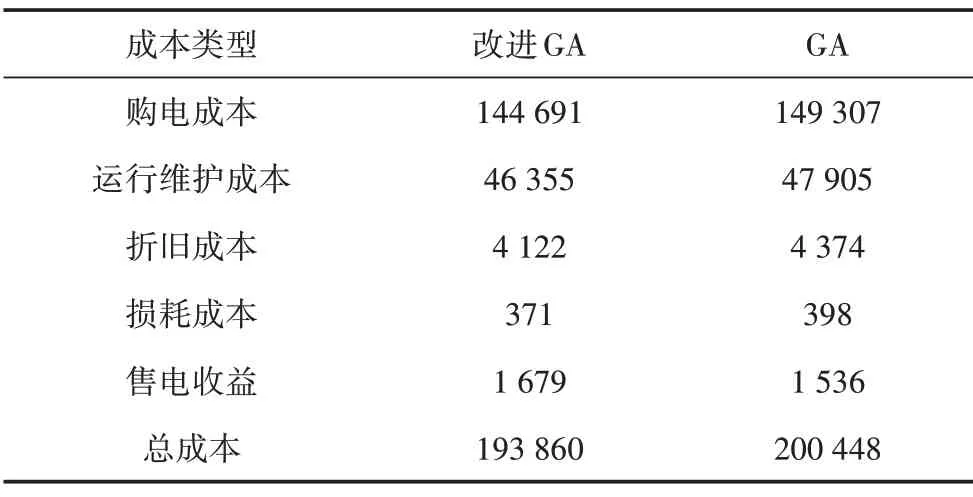
表2 两种优化方法计算的各项成本 单位：元

4 结语

综合考虑主动配电网运行过程中产生的各项成本及约束条件，建立了以ADN 总成本最小为目标函数的ADN 经济优化调度模型。为了提高ADN 经济优化调度模型的计算精度，对遗传算法的交叉概率和突变概率进行改进，分别利用改进遗传算法和遗传算法对ADN 经济优化调度模型进行求解，改进遗传算法的计算结果下降了6 588 元，验证了改进遗传算法能够明显加快目标函数收敛，提高计算精度。