基于改进收敛交叉映射的厂级振荡源诊断

周学均，陈小强，谢 磊

（1.中电国际胡布发电有限公司,巴基斯坦 卡拉奇74200；2.中电华创电力技术研究有限公司，江苏 苏州215123；3.浙江大学 智能系统与控制研究所，浙江 杭州310027）

现代化工业过程规模庞大，有数百至数千个高度耦合的控制回路，为了使生产效率最大化，保证产品质量，所有关键回路必须处于或接近最佳状态下运行[1]。振荡是过程控制系统性能下降的常见原因[2]。Z震荡可以在一个控制回路中产生并传播到其他单元，形成厂级振荡[3]。这些震荡有可能造成能源和材料的浪费，产品质量波动，甚至威胁控制系统的安全性。因此，对工业过程回路进行准确的因果分析，快速查明故障根源并采取相应的纠正措施，是保证安全生产和提高经济效益的关键。然而，由于工业控制系统中采集的数据往往被非平稳因素、噪声、周期项等干扰，对振荡源进行定位是非常有挑战的任务，因此大量的因果关系分析方法被用于震荡源的定位研究。

文献[4]使用互相关分析法来进行因果分析。方法虽然简单，但不适用于非线性的情况。文献[5]将主成分分析与多变量格兰杰因果关系结合起来进行厂级振荡的定位。格兰杰因果方法是一个广泛应用的方法，但对变量独立性和线性具有较严苛的要求。除了这些时域的因果分析方法，谱格兰杰、偏有向相干[6]、有向传递函数[7]等一些频域的方法也被开发出来。然而，谱格兰杰是基于傅里叶变换的方法，因此只能适用于线性平稳过程。偏有向相关和有向传递函数能描述因果方向，但是不能定量衡量因果影响。

上述方法局限于分析线性数据，但工业过程往往是非线性的。贝叶斯网络利用图结构描述变量之间的因果关系，然而它是一个有向无环图，因此不适用于动态过程。而且贝叶斯网络中的概率缺乏直观的物理意义，难以被工程师接受。

文献[8]提出了一种新的因果分析方法——收敛交叉映射（Convergent Cross Mapping，CCM），用于复杂系统中的变量关系分析。CCM主要基于Takens引理，即如果变量X是变量Y的原因，那么X的历史信息能够从Y中复现。CCM使用单纯形投影量化X和Y的状态依赖关系，估计状态之间的Pearson相关系数用于衡量交叉映射能力，这种能力对应着因果影响程度。CCM已经在各种工业过程中得到广泛应用，但基本CCM的收敛判据存在主观性，因此文献[9]提出了一种迟延CCM。迟延CCM认为原因变量和结果变量之间存在时间上的滞后，最强的因果作用应该出现在迟延处。迟延CCM克服了基本CCM的主观性，是近些年应用最为广泛、效果最好的关于CCM的研究成果。但是，当迟延CCM应用分析控制过程中的振荡信号时，噪声和周期项会损害CCM的可靠性。因此本文将经验模式分解（Empirical Mode Decomposition，EMD）[10]与去趋势波动分析（Detrended Fluctuation Analysis，DFA）[11]相结合实现消噪，并且利用奇异谱分析（Singular Spectrum Analysis，SSA）[12]消除周期项。将去噪去周期后的信号应用迟滞CCM进行分析,能准确确认回路之间的因果关系并定位故障源。最后，通过案例验证了所提出方法优势。

1 CCM简介

1.1 基本CCM

文献[13]采用CCM方法分析非线性系统中变量之间的因果关系。CCM假定如果变量X对变量Y具有结果影响，记作X→Y，那么Y将会包含X的信息。相应的因果关系能够通过X和Y的重构流形之间的关系来度量。具体来说，来自同一个动态系统的两个样本长度为N的离散时间序列X（t）、Y（t），X（t）的时间滞后嵌入向量可表示为：

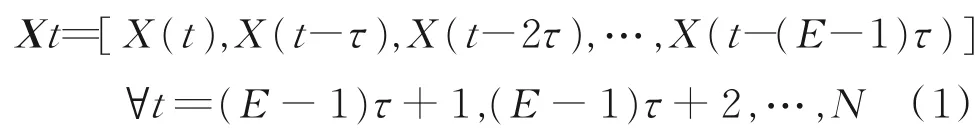
式中，E为嵌入维度；τ为迟延参数（默认为1）；X t为X（t）的阴影流形MX。当变量X是变量Y的原因时（X→Y），由于结果变量Y是原因变量X的特征信息，因此可以从Y中恢复关于X的状态信息，但是原因变量X没有结果变量Y的特征信息，因此不能从X中获取Y的状态信息。判断X→Y方向的因果关系时，CCM方法先通过测量Y的历史值，再计算X状态的可信度来判断因果关系。在CCM方法中，通过MY估计值X的准确度来反映变量X对变量Y的因果程度，可用相关系数ρ（标准皮尔森相关系数ρ(X,ˆ(t)|MY)）表示：

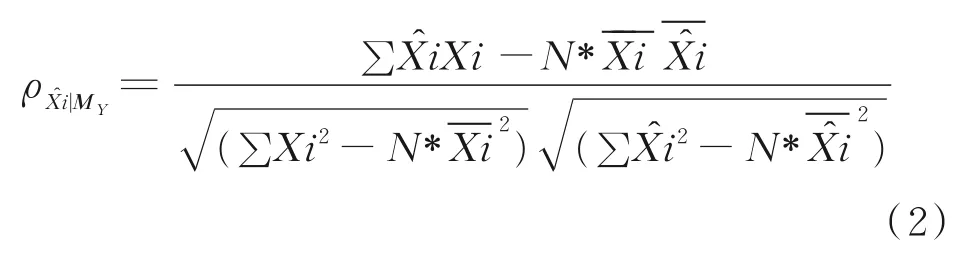
式中，N*为嵌入向量的个数。ρXˆ(t)|MY和X对Y的影响程度正相关。

收敛性是区分简单相关性和因果关系的一个重要指标，也是CCM的一个重要特性。收敛是指CCM估计的精度随着时序长度L的增大而提高。在实际应用中，收敛受系统误差、随机噪声和时间序列长度等因素影响。因此，基于CCM方法分析的因果关系通过相关系数ρ来证明，理论上ρ会随着时间序列长度的增大而收敛。

1.2 迟滞CCM

传统CCM方法已广泛应用于低中耦合度的动态系统的因果分析，但其无法解决“广义同步”现象，即如果X对Y的影响很大，则Y的内在动力从属于X，导致“同步”现象的出现。文献[13]提出了迟延CCM以解决这个问题。迟延CCM利用MY去估计Xt＋λ，其中λ是滞后时间。实际上，可以取不同的λ来计算不同迟延下的交叉映射指标ρ。最大ρ值即对应最优迟延λ*。λ*≤0对应X→Y，因为λ*≤0意味着原因变量过去的信息包含在结果变量中；如果λ*＞0，则反映通过原因变量的未来信息能预测结果信息，这显然是不合理的。因此，λ*＞0意味着X→Y的关系不成立。这样迟延CCM就能自动客观地确定因果关系。这里使用一个耦合的洛伦兹系统来测试基本CCM和迟延CCM的表现。

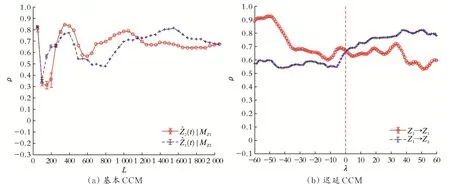
图1 基本CCM和迟延CCM的因果分析效果

2 改进CCM

2.1 噪声与周期性对CCM的不利影响

通过构建一个带扰动的四输入四输出耦合系统验证噪声与周期性对CCM的不利影响，其开环传递函数矩阵G(q－1)和扰动信号传递函数矩阵N(q－1)可表示为：

为了形成振荡传播路径，在第三回路L3中增加阀门粘滞故障，最终导致四个回路的全局振荡。CCM的周期和噪声影响结果如图2所示。图2中，红线表示错误的因果路径，红色箭头表示与实际情况不相吻合的因果关系方向，这些错误的因果关系方向导致无法判断振荡源到底在哪一回路。由图2可知，噪声和周期项对CCM具有不利影响。为了提高因果分析的可靠性，必须对信号进行去噪去周期的预处理。

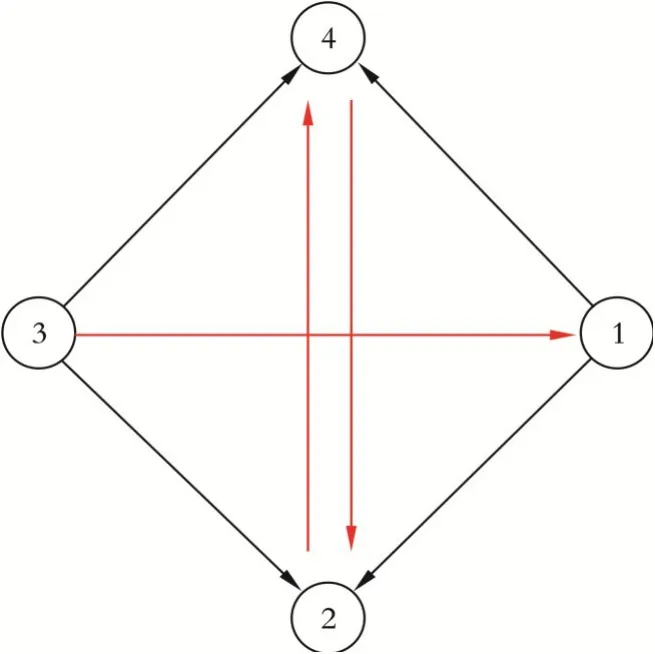
图2 CCM的周期和噪声影响结果

2.2 去噪与去周期

首先，介绍一种度量非平稳时间序列长程相关性的方法——去趋势波动分析（Detrended Fluctuation Analysis，DFA）方法。DFA算法的具体步骤为：

输入：X(t),t＝1,2,…,N；

（1）对时间序列X(t)求均值并累加：

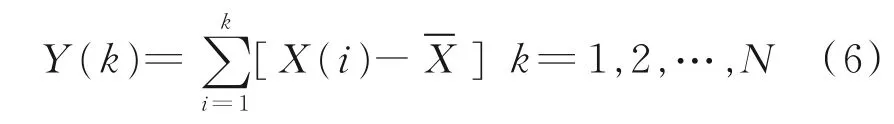
式中，Xˉ为X(i)平均值；Y(k)为累加时间序列。

（2）利用标准皮尔森相关系数对Y(k)划分长度为n的等长区间。用最小二乘估计法得到区间序列的趋势值Yn(k)。

（3）去除区间序列的趋势值，即将Yn(k)从Y(k)中去除。

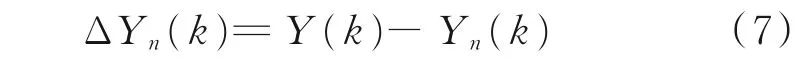
（4）计算均方根波动函数：

式中，N为数据长度。

（5）增加n的值，重复步骤（1）—（4），得到波动函数F(n)。如果满足F(n)∝nα，则定义α为度量因子。设置阈值为0.5，如果0＜α＜0.5，即时序X(t)有短期记忆性；α＝0.5表示X(t)为一个随机过程；α＞0.5则表示X(t)有长期记忆性。

输出：α。

将经验模态分解与DFA算法相结合，用经验模态分解得到信号的各个模态，再计算所有模态（包含残余分量）的度量因子α，进而判断其是否为噪声。

奇异谱分析方法（Singular Spectrum Analysis，SSA）是一种强大的时间序列分析方法，具有以下优点：

（1）适用于非平稳非线性时间序列。

（2）分解信号具有实际物理意义，如缓慢变化的趋势项、振荡分量以及噪声等。SSA算法的具体步骤为：

输入：Y(t),t＝1,2,…,N；

（1）嵌入。将累加时间序列Y(t)进行时间滞后表示为：

式中，i＝1,2,…,K，K＝N－M＋1；M为窗口长度。轨迹矩阵表示为：

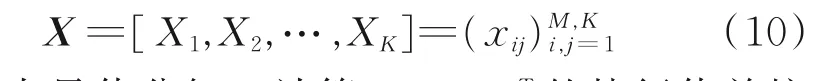
（2）奇异值分解。计算S＝XXT的特征值并按幅值降序排列（λ1≥λ2≥…≥λM≥0），设置d＝max(i)(λi＞0)＝rank(X)，则X的SVD结果为：

即计算逆对角线上元素的平均值。将XIk转化为与Y(t)长度相同的时间序列，则Y(t)就可以由m个长度为N的时间序列重构为：

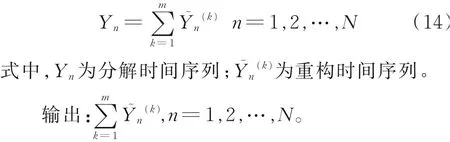
SSA方法基于时间序列协方差矩阵进行分析，该方法对时间序列的长度没有要求，并且也适用于短时间序列。

对信号进行SSA分解可以获得一系列特征值以及相应的特征向量和重构时间序列。特征向量及其相应的重构时间序列具有相同的属性。通常情况下，占比较大的特征值对应趋势项，两个相近的特征值对应周期项，递减缓慢的特征值序列对应噪声项。去噪去周期的CCM流程如图3所示。通过去噪去周期的步骤，改进后的CCM的因果分析效果更加可靠准确。

图3 去噪去周期的CCM流程

3 仿真实验

为验证所提方法的有效性，将该方法应用到四回路仿真控制系统上。去噪去周期后的CCM的结果如图4所示。

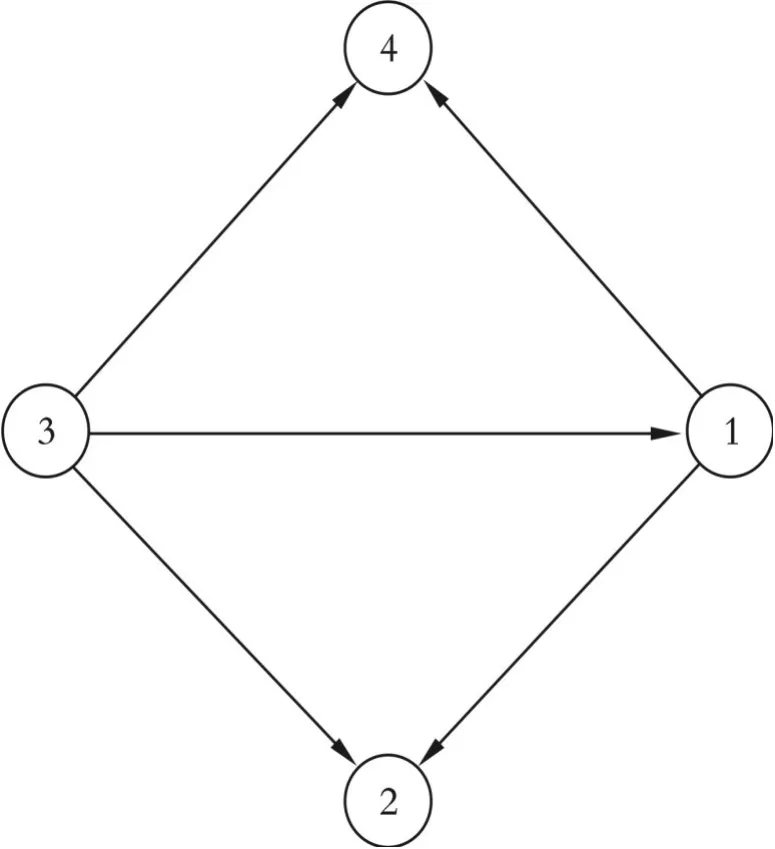
图4 去噪去周期后的CCM的结果

从图4可以看出，没有错误的因果关系方向，所提方法的因果分析结果与预设的系统结构完全一致，也与已有研究结果相吻合[6]，因此所提方法有效且明显改进了标准CCM的分析效果，对于准确分析因果关系是非常有必要的。

4 工业案例

为了验证所提方法在工业控制系统中的实用效果，采用田纳西－伊斯曼（TE）仿真平台作为实验对象。本文研究TE过程其中的17个主要回路。TE过程采样间隔为0.1 h，共运行72.0 h。系统稳定运行20.0 h后，在第16回路加入振荡扰动，最终引发17个回路发生全局振荡。按照文献[13]的方法将因果结构图转化为基于改进CCM的因果流图如图5所示。从图5中可知，第16和第17个变量所对应的回路是潜在的振荡源。因为第16和第17个变量都在同一个回路中，且数值越大表明越有可能是振荡源，所以将第16或者第17个变量识别为震荡源是准确的。通过所提出的改进CCM方法准确地找到了TE工业过程的振荡源，这说明该方法具有工业实际有效性。

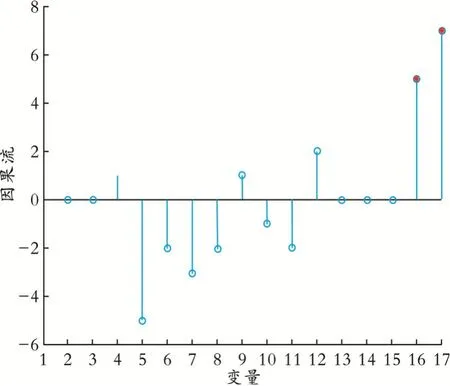
图5 基于改进CCM的因果流图

5 结 论

提出了一种基于去噪和去周期的CCM因果分析算法框架。首先，研究了噪声和周期性的不利影响。然后，将EMD和FDA结合起来实现去噪。用SSA去除周期性。仿真结果表明，所提方法能够有效地改善CCM的性能，可以减少对因果关系的误判。最后，将所提出方法应用于TE过程，以找出引起全局振荡的振荡源。应用结果表明，该方法对过程控制系统的振荡源定位有效。