基于PCA-SVM的DCT汽车驾驶员起步意图识别
2021-11-12刘海江吴雨林
刘海江,吴雨林
(同济大学 机械与能源工程学院,上海 201804)
目前,国内自主研发的DCT[1]和国外先进产品相比,整体上存在不小的差距,尤其是在起步方面,会出现起步性能不稳定、起步响应慢、起步过程传动系统抖动大、在某些恶劣行驶环境下汽车频繁起步换挡造成离合器过热甚至烧蚀等问题。而驾驶员在汽车行驶过程中起着决定性作用,知晓驾驶员起步意图不仅能够对驾驶员的驾驶行为和驾驶规律进行一定的预测,还能够为后续研究DCT控制系统的智能化控制提供有利依据。因此,有必要准确辨识驾驶员的准确起步意图,为DCT汽车的后续研制提供参考。
刘欣等[2]以模糊控制算法为基础,提出一种利用单片机来表现驾驶员的起步意图的方法,但这只是利用Matlab进行的仿真分析,没有进行实车验证,不能保证其能够在实际驾驶情况中充分考虑驾驶员的起步意愿。DAI等[3]分析了油门踏板开度及其一阶导数和二阶导数对起步意图的影响,并采用隐马尔可夫模型(Hidden Markov Model,HMM)对起步意图进行辨识,但是其识别准确率为80%,仍然有待提高。王姝等[4]基于前人经验,将平路起步看作一段时间内驾驶员对油门踏板、制动踏板等的一系列动作的组合,并采用双层HMM识别驾驶员的起步意图。胡锐、陈勇[5]对纯电动车起步过程进行动力学分析,基于模糊控制理论设计了驾驶员意图双模糊辨识系统,可以准确辨识出驾驶员起步意图。但是,他们只考虑到了起步过程中驾驶员因为驾驶意愿对汽车施加的操作,并没有考虑到车辆在起步过程中对驾驶员进行的反馈。LI Liang等[6]将加速踏板开度的统计规律作为输入参数,提出了一种基于人工误差反向传播神经网络的驾驶员起动意图识别方法,识别正确率大于95%,但是其将整个起步过程意图单一化,没有考虑到驾驶员在起步过程中可能根据车辆反馈出现意图的变化。
上述研究或是识别准确率不高,或是没有充分考虑汽车起步时的驾驶员和汽车进行的双向交互过程。针对以上问题,本文通过分析在平直道路起步过程中DCT车辆的人-车交互过程,得到表达驾驶员驾驶意愿的分析参数油门踏板开度,以及表达车辆对驾驶员反馈的分析参数纵向加速度;通过K均值聚类(K-means)对实车试验得到的起步数据进行意图划分;通过主成分分析(Principal Component Analysis,PCA)法对所选取的特征值进行相关性分析,并进行降维得到新的主成分;最后构建基于支持向量机(Support Vector Machine,SVM)的起步意图辨识模型,用来准确识别起步过程中驾驶员的起步意图。
1 起步意图分析
1.1 起步意图的定义
起步指的是驾驶员通过踩踏油门踏板等操作使汽车从完全静止的状态转变为有一定速度的运动状态的过程。驾驶员可以根据自身需求、路况和环境等进行不同程度的起步操作。根据专家的经验,起步过程可以分为缓慢起步、一般起步和紧急起步[7-8]。缓慢起步指的是驾驶员缓慢轻踏油门踏板至某一较小开度,让车辆的起步速度平缓增加,注重车辆起步的平顺性;一般起步指的是驾驶员以正常速度踩踏油门踏板至一定的开度,对车辆的起步快慢和起步平顺性均无特殊要求;紧急起步指的是驾驶员快速踩踏油门踏板至很大开度,让汽车获得尽可能大的起步加速度,追求汽车的快速起步而非平顺性。
汽车起步过程是人-车交互的过程,驾驶员为实现初始的起步意图对汽车施加一系列动作,之后再根据车辆的反馈而调整其意图和动作,因此,有必要确定合理的意图辨识周期。而有研究显示[9],面对紧急情况时驾驶员的反应时间为0.2~0.4 s。因此,可以选择0.4 s作为起步意图的辨识周期,即将DCT汽车的起步过程以0.4 s为识别间隔划分为6个时间段,在不同的时间段上分别进行3类起步意图的界定。
1.2 起步意图分析参数选取
汽车起步是一个信息交换和控制的过程,如图1所示。根据相关研究[10],驾驶风格不同的驾驶员因相同的起步意图踩踏油门踏板时,油门踏板开度相近,而因不同的起步意图踩踏油门踏板时,油门踏板开度有明显的差异。这说明驾驶员能够通过踩踏油门踏板的速度和深度来表达其起步意愿,所以选择油门踏板开度作为起步意图的一个分析参数。根据文献[11],驾驶员内耳的前庭器官相当于一个传感器,可以感知到纵向加速度。这说明纵向加速度可以作为DCT汽车对于驾驶员操作的反馈,匹配驾驶员的主观感受,所以选取纵向加速度作为起步意图的分析参数。

图1 汽车起步的信息交换和控制过程
1.3 起步试验方案设计
本试验与国内某主机厂合作,选择符合GB/T 12534—1990《汽车道路试验方法通则》要求的该主机厂1.5T-DCT汽车作为试验用车。为了控制环境变量,且考虑到车辆起步一般为平路起步,所以试验选择在干燥、整洁的平直道路上进行。试验采集设备包括分辨率为0.04905 m/s2的加速度测量设备和采样频率为100 Hz的数据采集系统。可以通过CAN总线和x/y轴加速度传感器获得油门踏板开度信号和纵向加速度信号。结合该主机厂专业驾驶员的驾驶评估经验,分别以不同的踩踏速度将油门踏板踩到若干个指定的油门开度。进行多次重复试验,得到140组起步试验数据。
1.4 基于K均值聚类的起步意图界定
K均值聚类算法是一种迭代求解的算法,具有无监督、迭代速度快的特性[12],可以用于已知聚类簇数k值数据的划分,因此选择该方法界定驾驶员起步时的缓慢操作、一般操作和紧急操作。对于指定的k个簇,K均值聚类的优化目标是使所有簇内样本的离差平方之和为最小,其优化目标如式(1)所示。

式中:x(u)为属于第v个簇的样本u;γ(v)为第v个簇的簇中心;nv为第v个簇的样本总量。
而且本文所研究的起步意图类别有3个,是已确定的,因此,在对试验所得的140组起步试验数据进行预处理,并以0.4 s为间隔分割完毕之后,分别选取每一个时间段内的油门踏板均值、纵向加速度均值作为特征值,利用K均值聚类算法对驾驶员的3种起步意图界限值进行确定。以0~0.4 s内DCT汽车的起步数据为例,其聚类流程为:确定类别数目为k=3;选取初始聚类中心点(1.65, 0.46)、(34.88, 1.13)、(70.14, 0.65);分别计算其余样本和这3个聚类中心点的距离,并根据各样本与这3个聚类中心的最小距离确定其类别;重新计算3个簇中样本的均值,并以均值作为新的聚类中心;在经过6次迭代之后,聚类中心变化稳定,从而得到最终的聚类中心(11.60, 0.24)、(33.82, 0.27)、(54.13,0.42)。其余时间段内的驾驶员起步意图数据集划分过程与之类似,不再赘述。
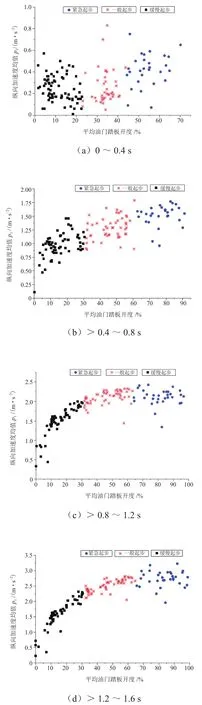
所有时间段的起步意图聚类中心见表1,聚类结果如图2所示。可以看出,不同起步意图的聚类中心有较为显著的差异,在各个时间段内相同起步意图的特征点分布集中。在0~0.4 s内不同起步意图之间的纵向加速度分布相近,但是依靠油门踏板开度的明显差异,仍然能够很好地区分这3种不同的起步意图;0.4 s后随着时间的推移,不同起步意图间纵向加速度的分布差异也越来越明显,综合油门踏板开度和纵向加速度可以确定不同起步意图的显著界限。因此,基于K均值聚类对驾驶员的起步意图进行划分是合理的。
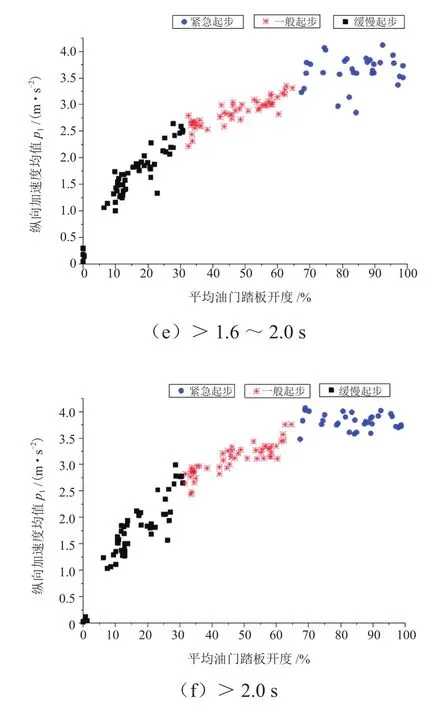
图2 各时间段驾驶员起步意图聚类结果
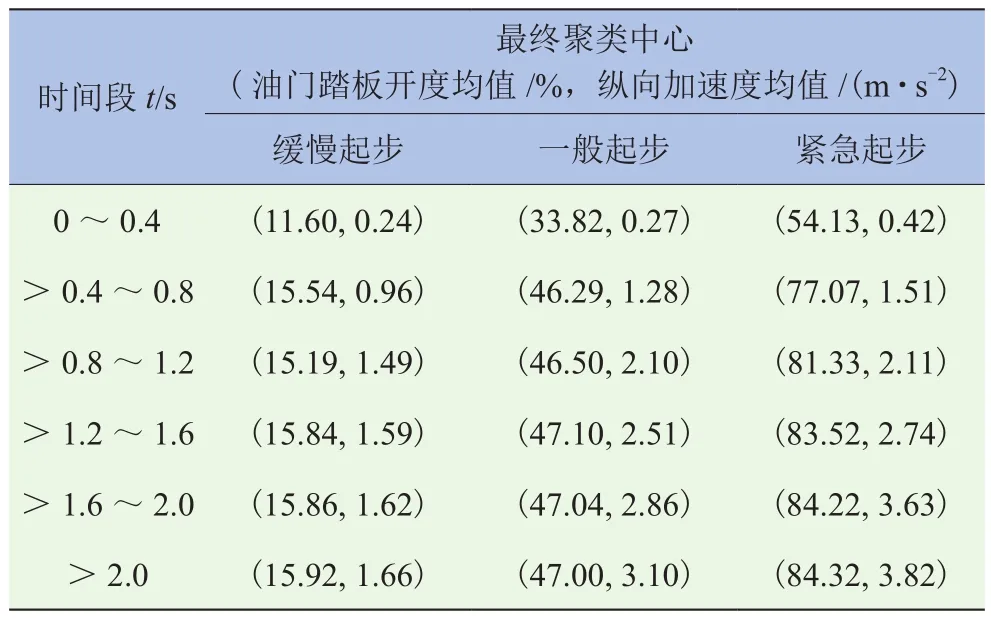
表1 各个时间段起步意图最终聚类中心
2 构建起步意图识别模型
2.1 基于PCA法的特征提取
PCA法[13]是一种将t个相关的原始特征p1,p2,....,pt经由线性变换组成新的互不相关的r个新特征Q1,Q2, ...,Qr的特征降维方法,可用如下模型表示:

式中:aij为主成分系数,(i= 1,2, … ,r;j= 1,2,… ,t)。
然而PCA的运用依赖于变量间的相关关系,因此,在进行PCA之前要进行相关性分析。KMO(Kaiser-Meyer-Olkin)检验统计量用于比较样本相关系数和样本偏相关系数,可以用来检验样本是否适合进行PCA。它的取值在0~1之间,值越接近1,则说明样本越适合进行PCA,一般要求该值大于0.5。巴特利特球形度检验(Bartlett’s Test of Sphericity)是一种检验各个变量之间相关性程度的检验方法,它的原假设是相关系数矩阵为单位矩阵,即原始变量互不相关。如果巴特利特球形检验的统计量较大,且其对应的相伴概率值小于用户心中显著性水平(一般认为小于0.05),那么就拒绝原假设,认为原始变量之间存在相关性,适合进行PCA。
石灰质量符合Ⅲ级以上标准,并在使用前7d进行充分消解。水泥采用32.5级复合硅酸盐水泥,初凝时间不小于4h,终凝时间不小于6h。
由于纵向加速度油门和踏板开度在时间序列上都是变化的,为了反映在某段时间内的这两个信号的稳态特征,选择纵向加速度均值、平均油门踏板开度作为初始特征值。根据文献[3]、文献[8]、文献[14]的研究,以油门踏板开度变化率作为特征值,可以反映出该时间段内油门踏板的动态特征,有效识别出驾驶员的驾驶意图,所以选取油门踏板开度变化率作为一个初始特征值。根据文献[15]的研究,不同驾驶意图下的纵向加速度均方差有着显著差异,所以选取纵向加速度均方差作为一个初始特征值。为了消除上述数据量纲、量级的差异,使之具有可比性,利用Z得分法(Z-score)进行标准化。以0~0.4 s的起步数据为例,将标准化后的纵向加速度均值(p1)、纵向加速度均方差(p2)、平均油门踏板开度(p3)、油门踏板开度变化率(p4)进行相关性分析,分析结果如表2和表3所示。其KMO取样适切性量数为0.654,大于0.5,而Bartlett球形度检验的显著性值小于0.001,说明这4个特征值之间存在着显著的耦合关联性,有产生较大的信息重叠,适合进行PCA。
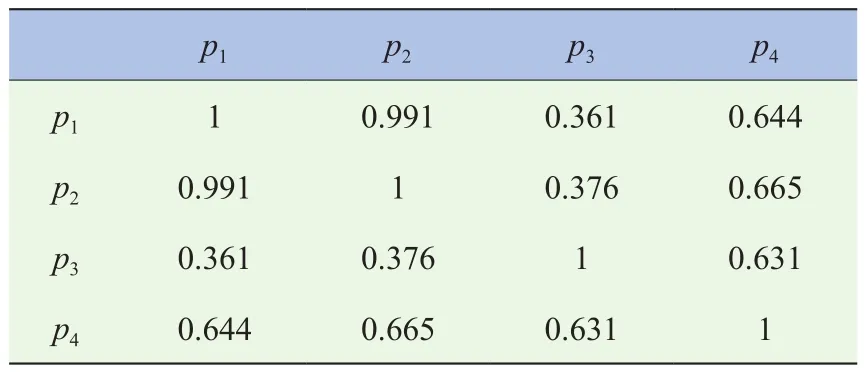
表2 相关系数矩阵
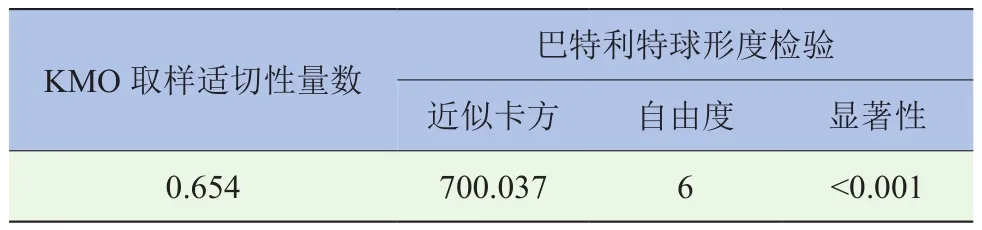
表3 KMO和巴特利特球形度检验
选取主成分的原则是尽可能多地保留重要信息,而衡量信息的指标是主成分的方差,方差越大,说明其含有的主成分信息量越大[17]。第k个主成分的方差贡献率为:
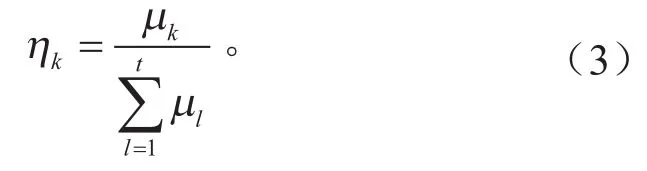
式中:µk为相关系数矩阵的特征值,k= 1, 2,…,t,且μ1>μ2> … >μt。其中特征值µk对应的单位特征向量为αk=(αk1,αk2, ...,αkt)。
根据特征值的累计方差贡献率来确定主成分个数r。按照经验,通常取累计方差贡献率大于或等于85%[16]。前m个主成分的累积方差贡献率为:

对0~0.4 s起步数据进行主成分分析后,得到的分析结果见表4。由表4可知,第1主成分累积方差贡献率为71.71%,小于85%,而第1主成分和第2主成分的累积方差贡献率达到92.73%,大于85%,所以可以确定主成分的个数为2。新主成分的表达式为:

表4 PCA分析结果
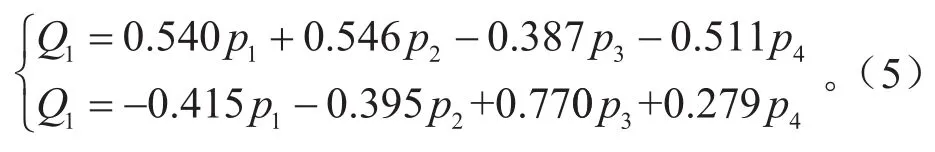
第1个主成分Q1能代表纵向加速度均值p1、纵向加速度均方差p2、油门踏板开度变化率p4的信息,而第2个主成分Q1能代表平均油门踏板开度p3的信息。将特征值所对应的单位特征向量作为主成分模型中的权重系数,排除人为干预带来的主观误差,这两个主成分可作为之后用于起步意图识别模型的新特征值。
2.2 基于SVM的起步意图识别
SVM作为一种有监督的学习算法,通过将低维线性不可分空间转变为高维线性可分空间,从而拥有较高的预测准确率。对所划分的每个时间段内都分别建立1个SVM模型,进行该时间段内的驾驶员起步意图识别。SVM算法的分类原理如下[18]:
对于线性可分的SVM,假设训练样本是(uk,vk),k=1, 2,…,N,v∈{-1 ,1},存在某分割超平面αTu+β=0将正负样本点进行区分,使不同类型的样本分布在该超平面的不同侧,此时形成距离为的“分割带”,使|αTuk+β|=1的样本点与该超平面的距离达到最小。考虑到本研究中设计的样本可能为非线性可分,即无法通过某线性超平面直接对样本点进行分割,必须通过某种变换φ(u)将其映射到高维空间中,于是引入松弛因子ξ和惩罚系数C修正优化目标和约束。采用拉格朗日(Lagrange)对偶性可以将该最优化问题等价转换:
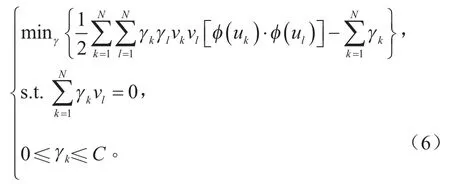
式中:γk,γl为 Lagrange 系数。
最终可获得最优分类函数,如式(7)所示。

最优分类函数也可转化为:

SVM模型的性能主要取决于惩罚系数C和核函数K。越大的惩罚系数会使“分割带”带宽越小,虽然提高了训练集上样本的正确分类个数,却可能导致模型过拟合;而惩罚系数过小会造成模型欠拟合。改变核函数的形式和它的参数会隐式地改变样本点从原始空间到高维空间的映射,在实际应用中,采用不同的核函数将导致出现不同的SVM算法。本研究基于专家经验知识,分别列举出多个惩罚系数C以及各个常用核函数K参数可能的取值,采用网格搜索法,对其进行排列组合,并将所有的组合结果生成“网格”;然后利用5折交叉验证,将起步数据集的训练集平均分成5份,其中4份为学习集,第5份为验证集,对所有“网格”进行评估,重复5次,从而确定最佳的惩罚系数C、核函数K以及该核函数的参数,结果见表5。
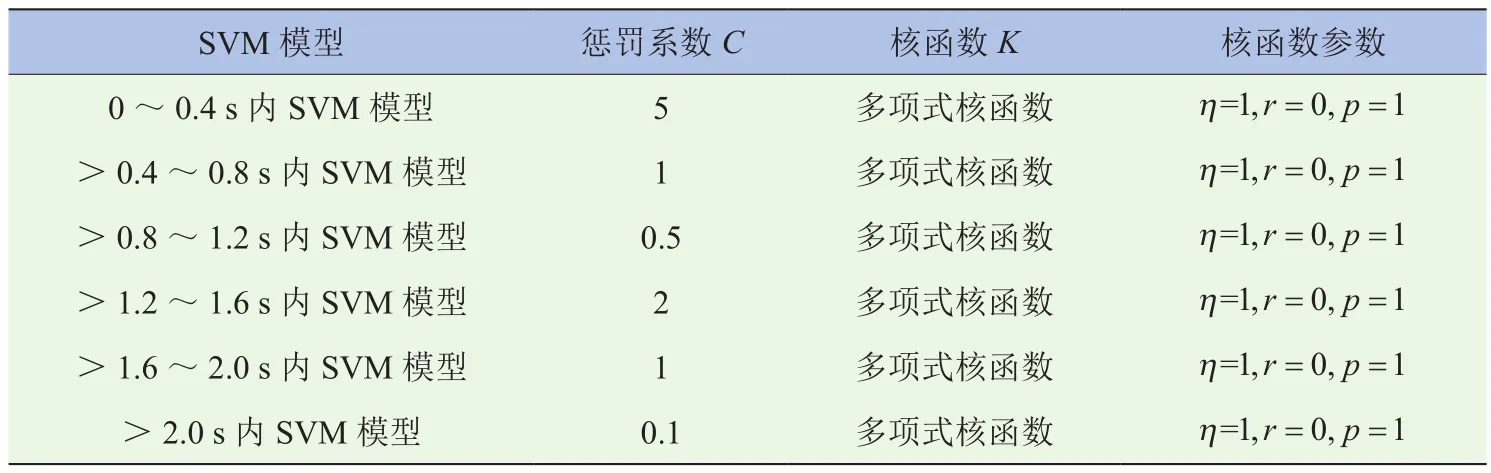
表5 SVM模型的参数选择
综上所述,基于PCA-SVM的起步意图识别流程如图3所示。首先设计并进行DCT汽车起步试验,获得所需要的起步数据集;在对测试参数进行缺失值处理、异常值剔除、去噪等预处理后,利用K均值聚类对各时间段内的起步意图进行界定;然后基于PCA确定新的特征值用于之后起步意图的识别;最后将起步数据集划分成训练集和测试集,利用训练集获得基于SVM的起步意图识别模型的惩罚系数和核函数,利用测试集对所训练出的模型性能进行验证。
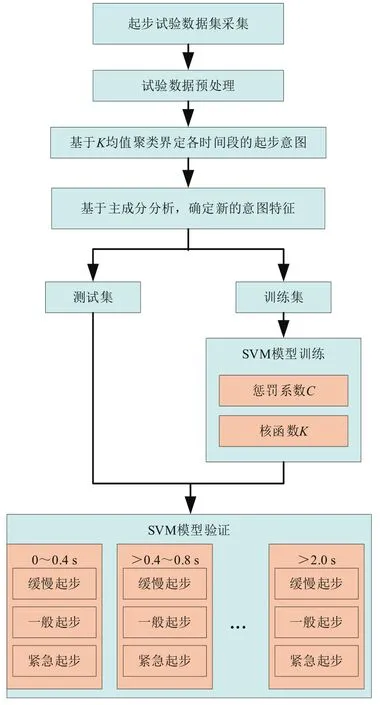
图3 基于PCA-SVM的起步意图识别流程
3 模型性能验证
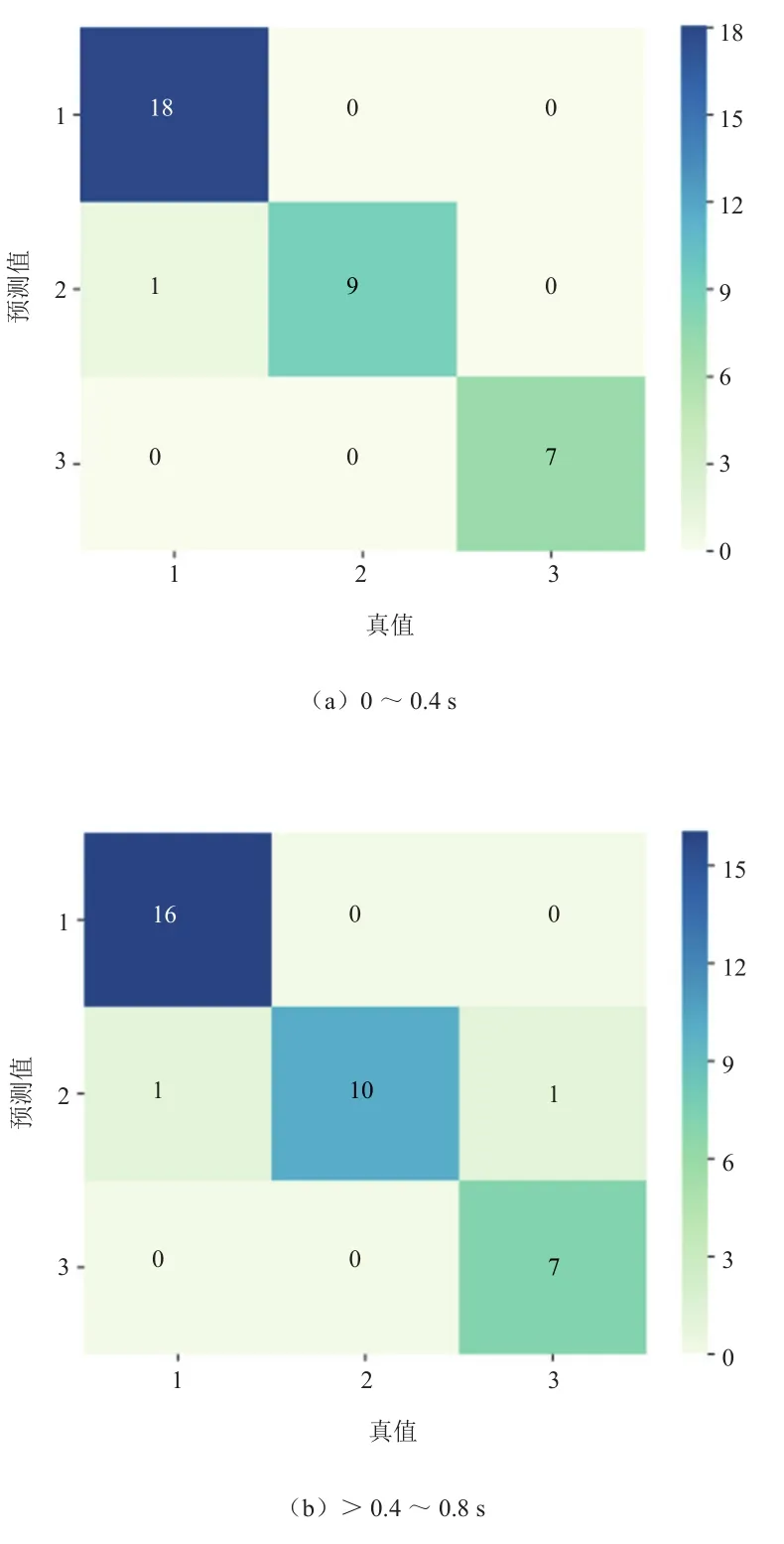
基于K均值聚类得到的各时间段内不同起步意图的样本数量见表6,单个起步样本包含经由K均值聚类得到的意图标签和经由PCA后得到的新特征值。采用留出法,按照3∶1将这6个时间段内的起步数据集划分为训练样本集和测试样本集;利用Python软件,根据训练样本集分别完成6个SVM模型的训练;将测试样本集送入训练好的SVM进行起步意图识别,并与原本的意图标签进行对比以检验模型的识别效果。以此得到的驾驶员起步意图识别结果混淆矩阵如图4所示,图中1代表缓慢起步,2代表一般起步,3代表紧急起步。

图4 起步意图识别结果混淆矩阵
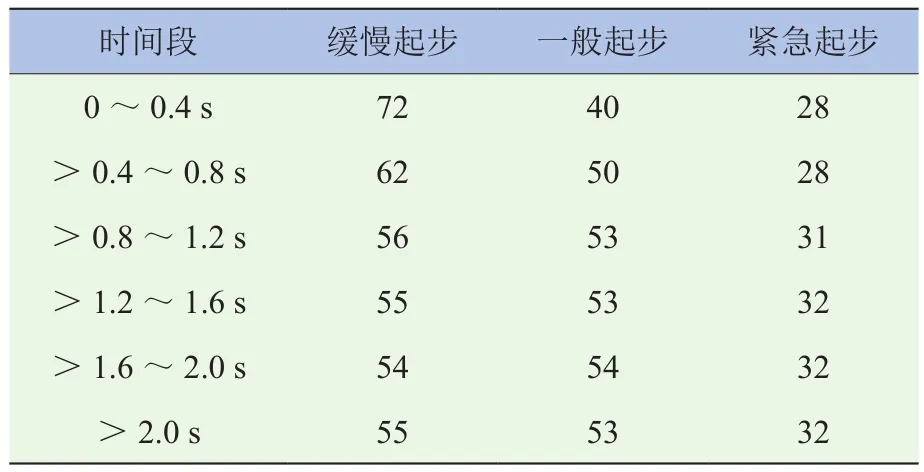
表6 各时间段内不同起步意图样本数量
能够正确识别出驾驶员的真实起步意图是DCT控制系统智能化的基础,因此,选取准确率和命中率作为评估该起步意图识别模型性能的指标。其中,准确率为识别正确的样本数占所有样本数的百分比;命中率为每类样本中识别正确的样本数与该类别样本数目的比值。计算不同起步阶段不同起步意图下的准确率和命中率,结果见表7。由表可知,这6个PCA-SVM模型的识别准确率均在90%以上,且平均识别准确率也高达94.92%;而只用线性SVM模型分别对这6个时间段的起步意图进行识别时,其识别准确率分别为62.86%、91.43%、91.43%、65.71%、82.46%、74.29%,平均识别准确率为78.03%,小于PCA-SVM模型的识别准确率,如图5和图6所示。而且,这6个PCA-SVM识别模型中对缓慢起步的识别命中率最高,均在90%以上;而对于一般起步和紧急起步的识别,最低的识别命中率也在85%以上,平均命中率分别为94.36%和89.74%。这表明了基于PCA-SVM的起步意图识别模型具有很高的识别准确率和命中率,泛化性能好。由表8可知,PCA-SVM模型和SVM模型的单个片段起步意图识别时间分别为0.008 s和0.002 s,均小于通常情况下驾驶员面对危急情形时的反应时间0.2~0.4 s,因此,PCA-SVM模型具有较好的实时性。
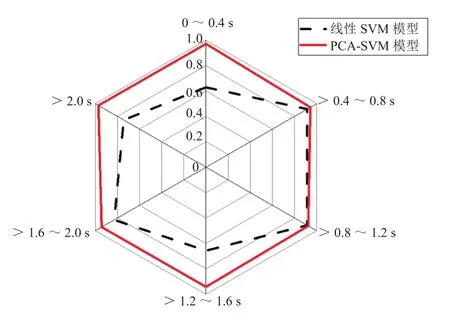
图5 线性SVM模型和PCA-SVM模型的识别准确率对比
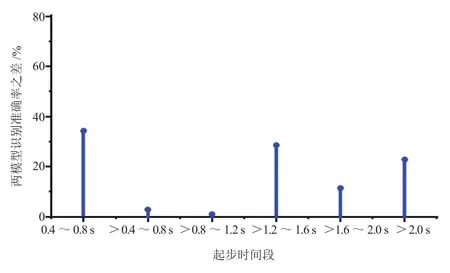
图6 PCA-SVM模型与线性SVM模型识别准确率之差
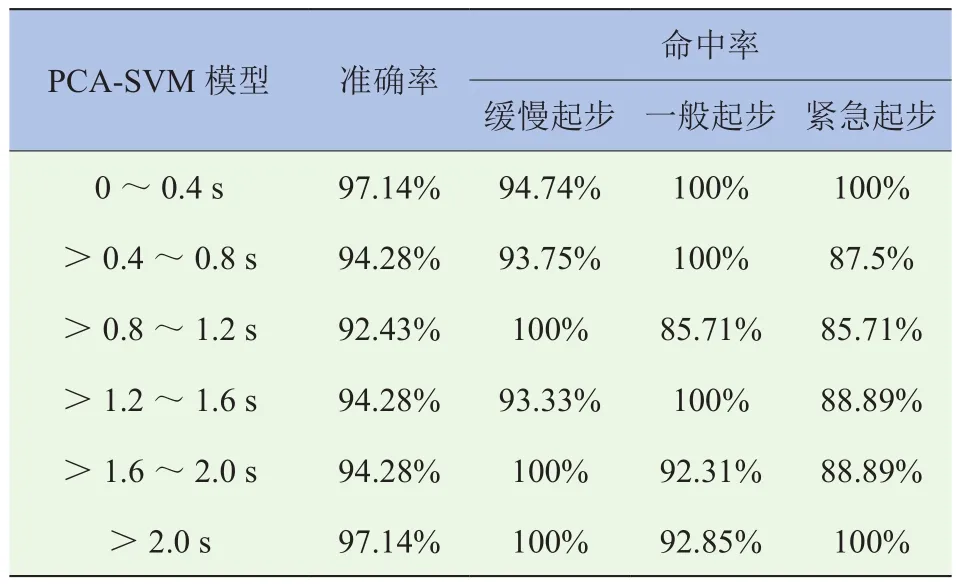
表7 PCA-SVM模型的识别准确率和命中率
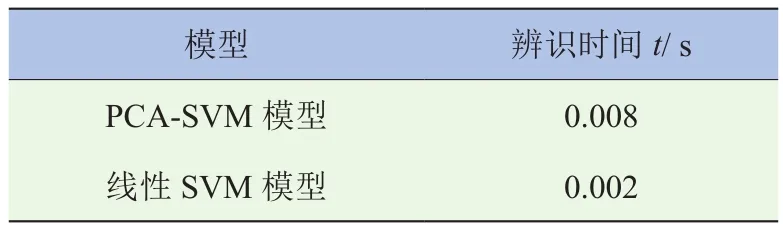
表8 PCA-SVM模型与线性SVM辨识时间对比
4 结论
本文提出了一种基于PCA-SVM模型的DCT汽车驾驶员起步意图识别方法,与其他起步意图识别方法相比,该方法不仅关注驾驶员起步意图的动态变化,而且识别效果较好,结论如下:
(1)在起步过程中,综合驾驶员的主观感受和DCT汽车的起步响应,将起步过程以0.4 s为间隔划分为6个时间段,充分考虑了驾驶员起步意图的变化。
(2)采用K均值聚类算法对DCT汽车驾驶员在各个时间段内的缓慢、一般和紧急操作进行了界定,得到具有明显差异性的3类不同的起步意图。
(3)针对原有特征值相关性较高的问题,提出了采用PCA进行降维的方法,得到新的特征值。
(4)构建了6个PCA-SVM模型,用作DCT汽车各个阶段起步意图的识别,其平均识别准确率达到94.92%,各起步意图的最低识别命中率也在85%以上,而且其模型单个片段的平均识别时间为0.008 s,实时性能良好。
