基于名义应力法的疲劳卡片构建方法研究

2021-11-12罗三峰王光耀万鑫铭赵奕炳

汽车工程学报 2021年5期

罗三峰，王光耀，万鑫铭，李阳，周佳，赵奕炳

（1.中国汽车工程研究院股份有限公司，重庆 401122；2.重庆市汽车轻量化工程技术研究中心，重庆 401122）

大多数机械零部件在工作环境中是承受载荷的，据相关资料统计，疲劳失效是机械结构失效最常见的形式，占全部力学破坏的50%～90%[1]，所以疲劳失效成为所有工程人员不得不考虑的一个问题。随着疲劳相关理论基础、计算机硬件与软件的不断发展，利用CAE技术对机械结构进行疲劳分析逐渐成为一种趋势。目前，常用商用疲劳仿真软件，如nCode、Femfat，大多应用名义应力法进行，疲劳分析工作流程如图1所示。

图1 疲劳分析软件分析流程

有限元分析软件对结构的应力应变以及变形结果进行分析，有限元结果导入至疲劳分析软件与载荷谱结合构建应力应变损伤历程和损伤参量历程。随后将根据疲劳累积损伤理论，即假设疲劳损伤和破坏是不断积累的，对损伤计数并计算损伤与疲劳寿命，Miner累积损伤理论[2]具体表达式为：

式中：D为总损伤；ni为载荷水平i下的循环数；Ni为载荷水平i作用下的疲劳寿命。

目前，国内外学者已利用疲劳分析软件对各类零部件进行了疲劳寿命分析，并取得了一定的成果。SINGH等[3]针对起重机吊钩，利用ANSYS workbench与nCode Designlife分别对其进行静力学分析和疲劳寿命分析，对比了不同结构设计对吊钩的安全性和经济性的影响，为吊钩的前期设计与结构优化提供了参考。基于相同原理，李成林等[4]、周美施等[5]对车架进行结构静强度分析与疲劳寿命计算，在车架的优化设计方面取得了一定的进展。但是由于试验条件限制，大部分研究未开展材料或者零部件的疲劳试验，利用经验公式预测材料疲劳卡片进行零部件的疲劳试验，可对不同结构的零部件进行对比分析，但零部件的预仿真预测寿命难以对标零部件的实际疲劳寿命。针对该类情况，苑大威等[6]对某武器击锤的失效形式进行了分析，发现击锤失效形式属于低周疲劳失效，随后通过材料的低周疲劳试验获取了应变-寿命曲线，基于应变-寿命曲线同时设置相应的修正系数创建了材料疲劳卡片，根据该材料疲劳卡片，利用Abaqus和nCode Designlife对武器击锤进行结构改进并对其疲劳寿命进行预测，最终结果表明，击锤仿真预测寿命与试验寿命保持一定的相关性。

综上所述，有限元疲劳寿命预测可应用于各行业，其预测精度的提高离不开有效的材料疲劳卡片，疲劳卡片反映了载荷水平与疲劳寿命的关系，目前大部分疲劳卡片对载荷水平的表述未能与有限元仿真计算过程进行有效结合。针对上述问题，本研究通过设计合理的材料试样疲劳试验，结合试验和有限元计算法来计算不同损伤参量，创建应用于疲劳寿命分析的材料疲劳卡片，同时设计验证试验对疲劳卡片的仿真精度进行评估，技术流程如图2所示。

图2 技术流程

1 疲劳卡片构建方法

1.1 高周疲劳试验设计

准确有效的试验数据是获取疲劳卡片的首要基础，采用高强中碳V系微合金钢进行疲劳试验，其材料静态力学性能见表1。将金属棒材按图2加工成标准高周疲劳试样[7]，试样加工过程中为减少表面粗糙度对试验的影响，将试样平行段精抛至表面粗糙度Ra0.2。试样在PLG-200高频疲劳试验机上进行，采取轴向应力控制，分别在应力比R=-1与R=0.06的条件下进行高周疲劳试验，试样以发现疲劳裂纹或疲劳断裂时的循环次数作为试样疲劳失效的终止寿命（试样疲劳失效判据）。

表1 试验材料静态力学性能

图4 PLG-200高频疲劳试验机

通过高周疲劳试验，最终获得如图5所示的不同载荷比下最大应力的S-N曲线，本文中的“最大应力”是指载荷与平行段横截面积的比值，在大多数工程应用中的疲劳卡片均以此为基础进行构建。

图5 不同载荷比条件试验结果

1.2 应力损伤参量的选取

由Miner累积损伤理论可知，计算疲劳寿命需要利用材料载荷水平-疲劳寿命对应关系，其中的载荷水平即疲劳损伤参量，采取何种损伤参量评价载荷水平直接关系到损伤的累计计算。而当采取名义应力法进行疲劳寿命计算时，利用S-N曲线表示载荷水平与疲劳寿命的关系，因此“S”是用应力度量的损伤参量。目前，商用疲劳分析软件的应力疲劳损伤参量包含最大主应力σMP、绝对最大主应力σAMP、无符号等效应力σVM、带符号等效应力σSVM、无符号剪切应力σSh、带符号剪切应力σSSh、临界面损伤参量σCP。

疲劳裂纹主要由物体的表面开始萌发，为提高计算效率，进行疲劳寿命计算时一般仅考虑表面的应力状态，同时假设没有正应力与剪切应力作用于表面，则在表面处的应力张量可简化为仅有3个非零分量σxx、σyy、σxy。根据上述原理，将应力损伤参量分为两大类，其中临界面损伤参量σcp为一类，其余参量为另一类。本研究使用的临界面损伤参量以应力张量的3分量在不同角度的临界面上计算，计算公式为：

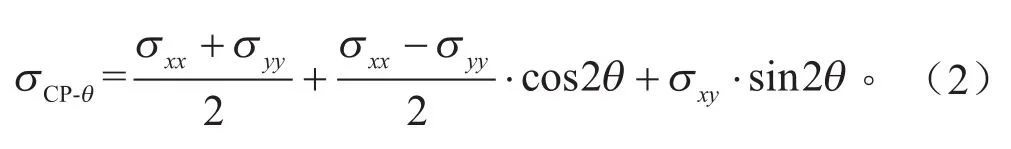
式中：σxx、σyy和σxy分别为应力张量的3个分量；θ为临界面法向量与局部坐标x轴的夹角，计算不同夹角θ的σCP-θ，并将其中的最大值作为最终的临界面损伤参量。

而其他应力（最大主应力σMP、绝对最大主应力σAMP、无符号等效应力σVM、带符号等效应力σSVP、无符号剪切应力σSh、带符号剪切应力σSSh）的损伤参量计算均是对第1主应力σ1、第2主应力σ2与第3主应力σ3进行计算，不同的应力疲劳损伤参量计算公式分别为：

上述的损伤参量也可分为两个小类，分别是“带符号”类损伤参量与“不带符号”类损伤参量，“带符号”类损伤参量可能是正值也有可能是负值，而“不带符号”类损伤参量均为正值。这是由于3个主应力依据定义，其代数值大小满足σ1＞σ2＞σ3，“带符号”类损伤参量对第1主应力σ1与第3主应力σ3的绝对值大小进行判定，第1主应力σ1绝对值大于第3主应力σ3绝对值，损伤参量为正值，反之则为负值。而材料受到拉应力和压应力时，材料的疲劳特性存在较大的差异，相同压应力作用下的疲劳寿命一般大于拉应力作用下的疲劳寿命，说明对损伤参量的正负进行判定是十分必要的，因此“不带符号”类损伤参量被首先排除，同时由于试验中采取轴向载荷加载，所以舍弃带符号剪切应力σSSh。综上所述，本研究采取临界面损伤参量σCP、绝对最大主应力σAMP和带符号等效应力σSVM作为损伤参量。

1.3 损伤参量的计算

为计算试验过程中的不同损伤参量，对试样（图3）建模后导入有限元软件中，按图6的方法对试样进行网格划分，并对试样的平行段网格适当细化，整体采用六面体网格，试样整体网格划分后包含2 044个单元和10 711个节点，随后将试样夹持端一端施加固定约束，另一端分别施加与试验中大小相同的轴向力。

图3 高周疲劳试样设计

图6 有限元计算损伤参量

分别对1.1节所述的疲劳试验中不同载荷下试样损伤参量进行计算，计算结果见表2。结果表明，临界面损伤参量与绝对最大主应力损伤参量计算结果相近，这是由于计算轴向加载试验σCP-θ总是在轴向上有最大值。

表2 损伤参量计算结果

1.4 疲劳卡片的创建

常见的S-N关系表述方法包含两种，一类是线性拟合后的标准S-N曲线，另一类是不拟合的多应力比S-N曲线。由于上文临界面损伤参量σCP与绝对最大主应力σAMP两种参量计算结果相近，因此将绝对最大主应力σAMP和带符号等效应力σSVM结合相应试验载荷的存活率50%疲劳寿命估计值，分别构建标准S-N疲劳卡片和多应力比S-N疲劳卡片，同时直接利用试验数据（图5）构建疲劳卡片进行对比分析，线性拟合后的标准S-N疲劳卡片如图7所示，线性拟合过程中转折寿命为1×107次。

图7 标准S-N疲劳卡片

2 疲劳卡片的验证

为验证不同类型的疲劳卡片的预测精度，设计应力比R=-0.5的高周疲劳试验，试样设计与1.1节中的一致，获取试样R=-0.5时3个载荷水平下的疲劳寿命。随后，分别利用不同的疲劳卡片对R=-0.5的疲劳试验进行预测。计算过程中，由于平均应力修正方法在平均应力不为0的条件下对计算结果影响巨大，所以利用不同平均应力修正方法对试验结果进行计算，修正方法包含古德曼（Goodman）修正、格伯（Gerber）修正和插值法修正[1]。疲劳卡片类别和应力修正方法见表3，预测结果如图8所示。

表3 疲劳卡片类别与应力修正方法

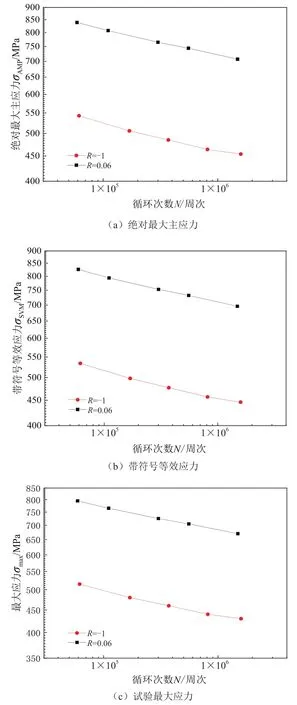
图8 多应力比S-N疲劳卡片

由图9可知，疲劳卡片采用的损伤参量类型、疲劳卡片表达形式以及计算的修正方法种类对于最终预测精度均存在不同程度的影响，通过对比分析预测结果表明：

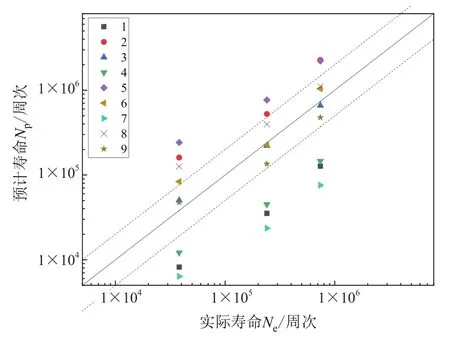
图9 不同疲劳卡片预测结果

（1）无论采取何种疲劳卡片，利用Goodman方法计算的预测寿命误差较大，预测结果均过于保守并落在2倍误差因子以外。

（2）采用Gerbera方法的预测精度略高于Goodman方法，但其预测结果偏激进，即预测结果均大于实际寿命且大部分预测结果仍旧落在2倍误差因子以外。

（3）采用多应力比疲劳卡片利用插值法修正的预测方法精度最高，应用不同损伤参量的多应力比疲劳卡片预测精度略有差异。其中，当采取绝对最大主应力作为损伤参量构建多应力比S-N疲劳卡片，同时利用插值法进行平均应力修正时，具备最好的综合预测能力，且在不同载荷水平下均能达到较好的预测精度，尤其在中高寿命范围内，预测误差在10%左右。