某SUV尾门模态性能分析及轻量化设计
2021-11-12段龙杨
段龙杨
某SUV尾门模态性能分析及轻量化设计
段龙杨1,2,3
(1.江铃汽车股份有限公司,江西 南昌 330200;2.江西省乘用车结构设计工程研究中心,江西 南昌 330200;3.江西省汽车噪声与振动重点实验室,江西 南昌 330200)
以某SUV尾门为研究对象,首先建立尾门有限元模型,对其进行自由模态分析,分析结果表明其前三阶频率均大于激励频率,符合动态性能要求。然后采用锤击法对其进行模态试验,试验结果表明其仿真结果与试验结果基本一致。最后对尾门的结构参数进行优化设计,得到其最优的厚度值,并且其重量减小了5.5%,实现了轻量化的效果。
尾门;有限元;模态;轻量化
引言
车门是车辆系统中最重要的部件之一,其主要由外板、内板、加强板及其附属件组成。车门的刚度性能和强度主要影响其疲劳性能和可靠性,其模态性能主要影响着车辆的舒适性。若车门与车身、路面和发动机等外界激励频率不匹配时,将使系统相互之间的耦合加强,造成车门振动增大,也容易产生共振风险,严重影响整车的舒适度。与此同时,随着能源越来越紧张和环境污染越来越严重,节能减排是汽车行业必须重视的问题。研究表明,车辆每减轻100 kg,燃油经济性可提升6 %,并且可以降低一定的尾气排放,因此车辆的轻量化是目前汽车领域重要的研究手段。为了研究某SUV尾门的模态性能,首先建立尾门有限元模型,对其进行模态性能分析,然后对其进行模态试验,验证有限元分析的正确性,最后对其进行轻量化设计,获取尾门的最优结构参数。
1 模态分析原理
基于结构振动力学理论可以获取尾门的运动方程[1]:
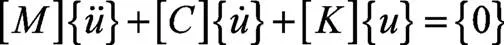
式中:[]表示尾门的质量矩阵;[]表示尾门的阻尼矩阵;[]表示尾门的刚度矩阵;{}为表示尾门的位移向量。
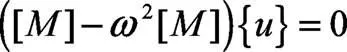
式中:表示尾门的固有频率,{}表示尾门的模态阵型。
2 建立尾门有限元模型
某SUV尾门主要由外板、内板和两侧加强板组成,外板的厚度为1.8 mm,内板的厚度为1.6 mm,加强板的厚度为2.0 mm,尾门的重量为23.6 kg,将其三维数字模型导入Hypermesh软件[2-3]中。由于尾门的外板、内板和加强板均属于薄的冲压钣金件,因此分别抽取它们的中性面,然后清理其几何表面,忽悠微小特征,并删除对模态性能影响比较小的零部件。根据尾门模型的实际尺寸,保证分析精度,并尽量减少计算时间,采用5 mm的四边形单元对尾门的各个部件进行网格划分,过渡区域可以采用三角形单元连接。外板与内板通过包边连接,采用四边形单元共节点连接。两侧加强板与内板通过焊缝连接,采用ACM单元连接能够较好的表征力学传递关系。尾门的材料牌号为DC01,其弹性模量为2.1E+5 MPa,泊松比为0.3,密度为7.85E+3 kg/m3。根据尾门的材料牌号和厚度建立相应的材料属性,以此建立尾门有限元模型,如图1所示。

图1 尾门有限元模型
3 模态性能分析
通过尾门的模态性能分析可以获取其模态频率及其阵型,能够识别出共振风险。尾门的自由模态性能分析是指不加载任何约束和载荷,因此基于尾门有限元模型,采用Nastran软件[4-5]不作任何约束,对其进行模态性能分析,得到其第一阶、第二阶和第三阶模态频率分别为35.7 Hz、62.3 Hz和76.4 Hz。
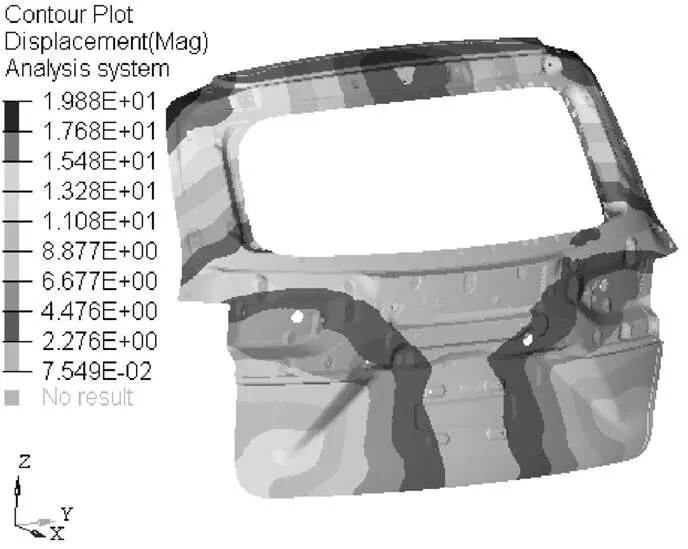
图2 尾门第一阶阵型云图
如图2所示,为尾门第一阶阵型云图。由图2可知,其阵型表现为整体扭转,其模态振幅最大为19.88 mm。
如图3所示,为尾门第二阶阵型云图。由图3可知,其阵型表现为整体弯曲,其模态振幅最大为19.15 mm。
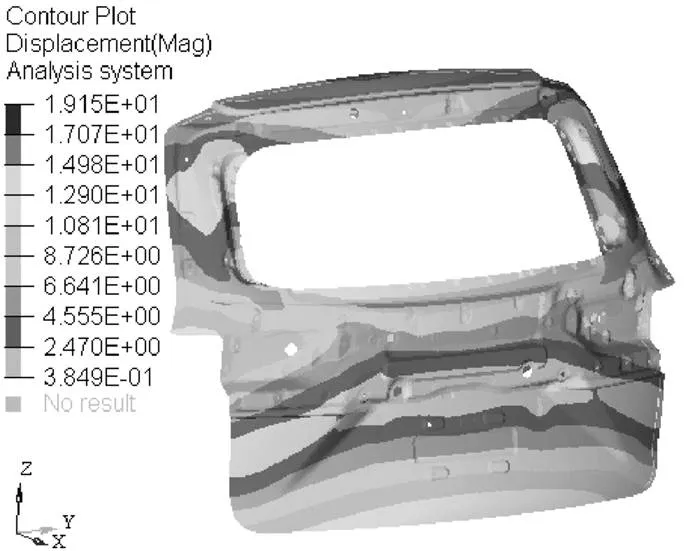
图3 尾门第二阶阵型云图
如图4所示,为尾门第三阶阵型云图。由图4可知,其阵型表现为中部凸起,其模态振幅最大为22.53 mm。
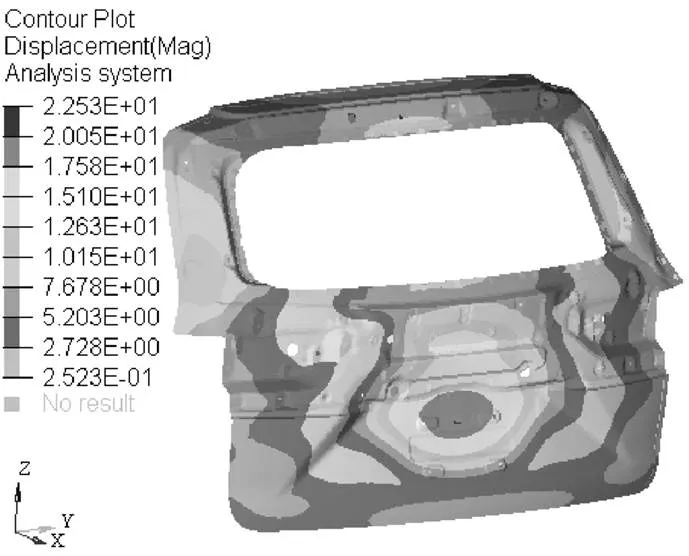
图4 尾门第三阶阵型云图
该SUV发动机的额定运行频率为30 Hz,路面的激励频率范围为10~20 Hz,因此尾门的模态频率有效地避开了外界的激励频率范围,不会产生共振,完全满足尾门的振动特性要求。
4 模态试验
为了校核有限元分析的准确性,将尾门采用弹性绳将尾门悬挂与试验台上,使其处于无约束状态,采用单点激励多点响应和锤击法对尾门进行模态试验,并基于频响函数法进行数据处理,得到其模态试验值及试验阵型。如图5~图7所示,分别为尾门的前三阶模态试验阵型。由图5~图7可知,尾门的前三阶试验阵型分别表现为扭转、弯曲和凸起,与模态仿真阵型相吻合。
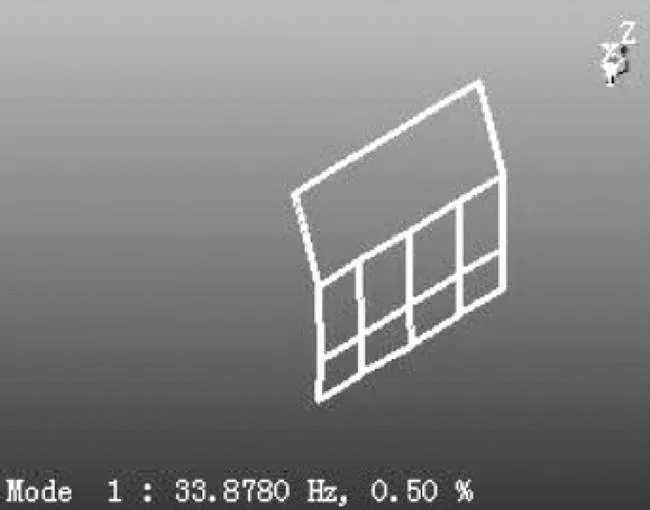
图5 尾门第一阶试验阵型
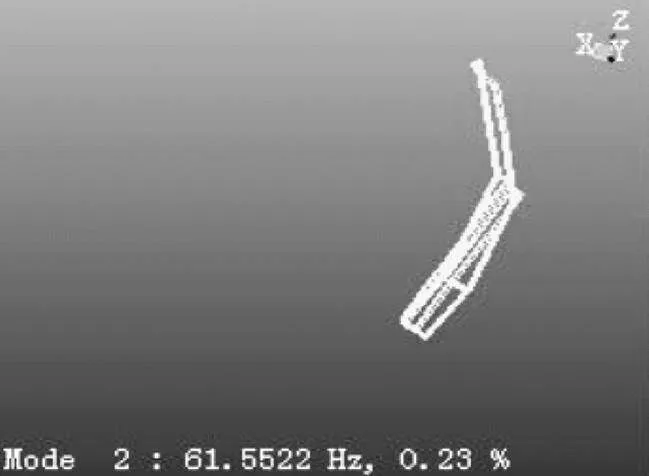
图6 尾门第二阶试验阵型

图7 尾门第三阶试验阵型
如表1所示为尾门的模态试验值与仿真值对比。由表1知,尾门的模态频率仿真值与试验值的误差率均在实际工程误差范围之内,进一步验证了模态性能分析的可靠性。
表1 模态仿真值与试验值对比
阶数仿真值试验值误差率 第一阶频率/Hz35.734.24.4% 第二阶频率/Hz62.360.13.7% 第三阶频率/Hz76.471.66.7%
5 轻量化设计
通过尾门的模态性能分析可知,其振动性能拥有足够的富余量,具有轻量化的空间,因此将尾门外板的厚度值、内板的厚度值和加强板的厚度值作为设计变量,将尾门重量最小化作为目标函数,将其第一阶模态频率大于33 Hz作为约束函数,采用第二代非劣排序遗传算法[6]对尾门进行结构优化,最终得到尾门外板的厚度为1.6 mm,内板的厚度为1.2 mm,加强板的厚度为1.5 mm。
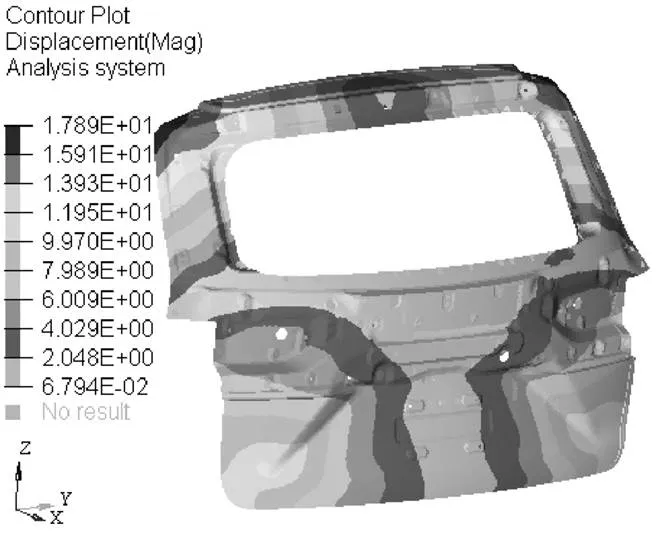
图8 优化之后的尾门第一阶阵型云图
优化之后尾门的前三阶固有频率分别为33.2 Hz、58.7 Hz和70.1 Hz,其模态频率仍然高于激励频率,符合性能要求。如图8~图10所示分别为优化之后尾门的前三阶阵型云图。由图8~图10可知,优化之后尾门的前三阶模态振幅最大分别为17.89 mm、17.24 mm和20.28 mm,其阵型与优化之前相同。
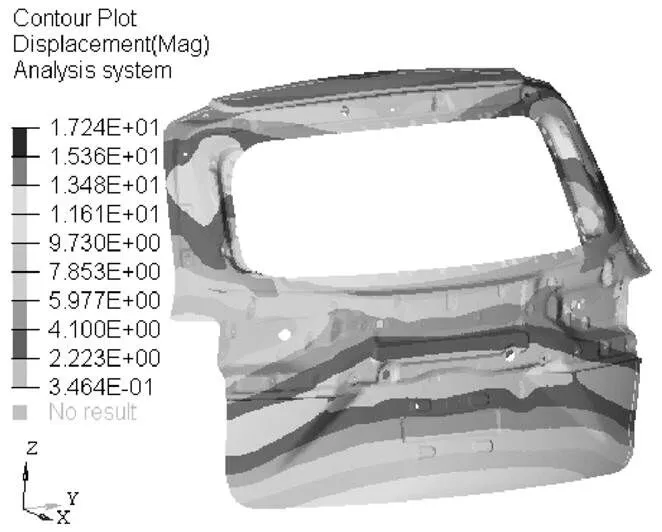
图9 优化之后的尾门第二阶阵型云图
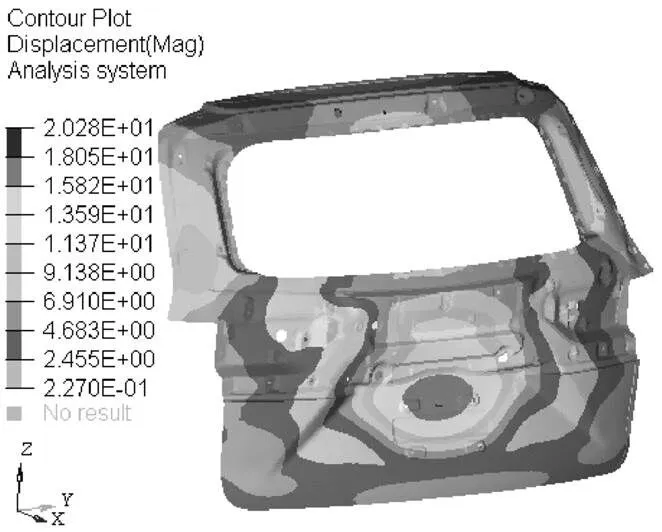
图10 优化之后的尾门第三阶阵型云图
与此同时,优化之后尾门的重量为22.3 kg,相对于优化之前,其重量减轻了5.5%,实现了轻量化的效果。
6 结论
基于CAE技术建立尾门有限元网格,对其进行自由模态性能分析,得到其前三阶固有频率分别为35.7 Hz、62.3 Hz和76.4 Hz,避开了外界激励频率,符合振动特性要求。采用单点激励多点响应方法对尾门进行模态试验,模态试验值与仿真值基本一致,误差率较小。采用第二代非劣排序遗传算法对尾门的结构进行优化设计,得到了尾门的最优厚度值,并且其重量减轻了5.5%,达到了轻量化的目的。
[1] 朱茂桃,陈亚洲.基于灵敏度方法的车门模态优化[J].重庆交通大学学报(自然科学版),2014,33(1):139-143.
[2] 龙岩,蒋凌山,刘雪强,等.某轿车车门轻量化与疲劳寿命多目标综合优化[J].中南大学学报(自然科学版),2019,50(11):2732-2742.
[3] 钱银超,刘向征,邓卫东,等.汽车车门有限元分析及综合性能优化[J].机械设计与制造,2018,(7):192-195.
[4] 秦训鹏,冯佳伟,王永亮,等.基于响应面方法的微型车车门模态分析与优化[J].中国机械工程,2017,28(14):1690-1695.
[5] 吕彩琴,王宏伟,孙权.某电动轿车车身结构优化与NVH性能提升[J].现代制造工程,2020(10):57-61.
[6] 刘昊,周成,于存贵.随车起重机伸缩臂截面多目标优化[J].机械设计与研究,2020,36(1):173-176.
Modal Performance Analysis and Lightweight Design of a SUV Tail Gate
DUAN Longyang1,2,3
( 1.Jiangling Motors Corporation Limited Company, Jiangxi Nanchang 330200;2.Passenger Car Structure Design Engineering Research Center of Jiangxi Province, Jiangxi Nanchang 330200;3.Key Laboratory of Automobile Noise and Vibration of Jiangxi Province, Jiangxi Nanchang 330200 )
The tail gate of an SUV was taked as the research object. Firstly, the tail gate finite element model was established, and it was modal analyzed, the analysised result showed that its first three frequencies were greater than the excitation frequency, so it could meet dynamic performance requirements. Secondly, it was modal tested by adopting hammer method, the test result showed that its simulation results were basically consistented with the experimental result. Lastly, the structure parameters of the tail gate were optimized, so the optimal thickness were obtained, and its weight was reduced by 5%, the lightweight effect was realized.
Tail gate; Finite element; Modal;Lightweight
U463.83+4
A
1671-7988(2021)20-104-04
U463.83+4
A
1671-7988(2021)20-104-04
10.16638/j.cnki.1671-7988.2021.020.025
段龙杨(1966—),男,高级工程师,硕士,就职于江铃汽车股份有限公司,主要从事车辆工程研究。
