受限水声阵列阵型定位算法比较研究

2022-07-28董真杰张维全郑琛瑶

现代电子技术 2022年15期

关键词：面阵求根阵型

董真杰，张维全，郑琛瑶

（中国人民解放军91388 部队，广东湛江 524022）

0 引言

选择匹配的阵列信号模型是阵列信号处理之前最关键的步骤。本文选择了多个二维面阵模型，用DOA估计算法分别加以验证，从不同方面进行比较，给用户提供客观评价，方便在水声定位工程实践中选择合适的信号处理方法。

1 受限水声阵列

水声定位系统硬件由多阵元水听器阵列组成，后续没有完成多路水声信道建设，仅有有限路采集通道，形成了一种受限的水声阵列阵型。为完成多目标定位，在硬件基础上增加了通道选择模块，用来快速实现阵型变换。模块采用FPGA 芯片，采用Verilog HDL 语言编写代码，设置阵型选择模式，每个模式可以代表下文中所选的对应阵型。用运算放大器对采集到的模拟信号完成放大后，采用带通滤波选择相同的通带频率和工作频率，保障各个信号通道基础信息设置一致。

2 二维面阵模型

为了简化分析，更快速准确地得到仿真结论，假设采用的信号源形式为：点辐射源、窄带信号，假定噪声为高斯白噪声，并且与信号源不相关，信号源的数量是已知的，也可以从计算中获取，接收阵列与信号源之间是远场环境。本文中应用的二维面阵有L 阵型、双L 阵型、均匀面阵型、“口”字阵型，信源至阵列的俯仰角定义为原点到信源的方向矢量与轴方向矢量间的夹角，方位角则是原点到信源的方向矢量在-平面上的投影与轴方向矢量之间的夹角。信源与接收阵之间满足远场条件，故用一点表示整个阵列。

L 阵型有+-1 个阵元，由轴上个阵元和轴上个阵元均匀构成，阵元间距为。假设有个信源，其DOA 为(θ,φ)（=1，2，…，），其中θ，φ分别为第个信源的俯仰角和方位角。

双L 阵型类似于L 阵型，结构图如图1 所示。

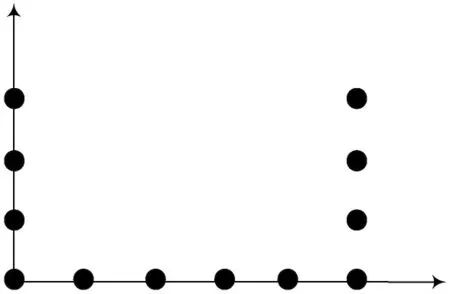
图1 双L 阵型

对于均匀面阵型，结构图如图2 所示，阵元数为×，均匀分布在平面上。信源数为，θ，φ分别代表第个信源的俯仰角和方位角。

选择适用于半湿润半干旱地区的双超产流模型作为汾河水库水文站控制流域的产流模型，单元体双超产流模型主要包括植物截留计算、微元入渗、超渗产流、超持产流、单元体蒸散发计算5个单元功能模块。汾河水库流域汇流采用瞬时单位线模型[8]。汾河水库流域河道流量演算模型采用水文学模型[4]。双超产流模型计算流程图见图2。

图2 均匀面阵型

“口”字阵型即由4 条线阵围成一个矩形，方向矩阵雷同于双L 阵型。

3 不同算法匹配阵型仿真比较

二维DOA 估计本文采用L 阵型、双L 阵型、均匀面阵型和“口”字阵型实现二维参数估计，多数二维DOA算法是在一维DOA 算法基础上针对二维空间提出的改进或推广方法。二维MUSIC 算法是二维DOA 估计的典型算法。本文针对不同阵型选用不同适配算法：二维MUSIC、求根MUSIC、ESPRIT 和降维MUSIC 算法定义均方根误差为：

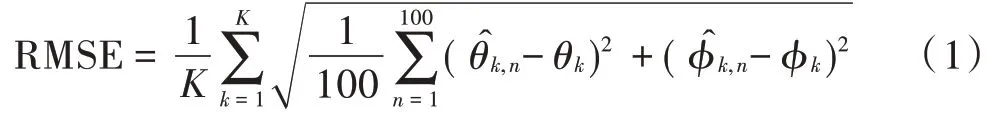
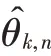
3.1 L 阵型-MUSIC 和求根MUSIC 算法

不同于一般两边等阵元数的L 阵型，由于硬件限制，轴方向只有4 个阵元，轴就会有9 个阵元，阵元数的不同使得两个角度的测量误差水平不同。2D-MUSIC算法利用空间谱函数进行二维的谱峰搜索，是一个经典的算法，具有普遍适用性，缺陷就是要进行空间二维角度搜索，运行时间长。求根MUSIC 算法用多项式求根的方法代替谱搜索，能大大降低运算量。

仿真条件：L 阵型，轴上有9 个阵元，轴上有4 个阵元，公用参考点阵元，假设3个信号互不相干，角度分别为（10°，20°），（30°，40°），（50°，70°），信噪比选用0 dB，5 dB，10 dB，15 dB，20 dB 和25 dB。使用MUSIC 和求根MUSIC 算法，MUSIC 算法取1°作为搜索步长。蒙特卡洛次数为100，图3、图4 分别为MUSIC 单次运算图和求根MUSIC 算法估计性能图，信噪比均为10 dB，快拍数为200。

图3 二维MUSIC 一次计算结果

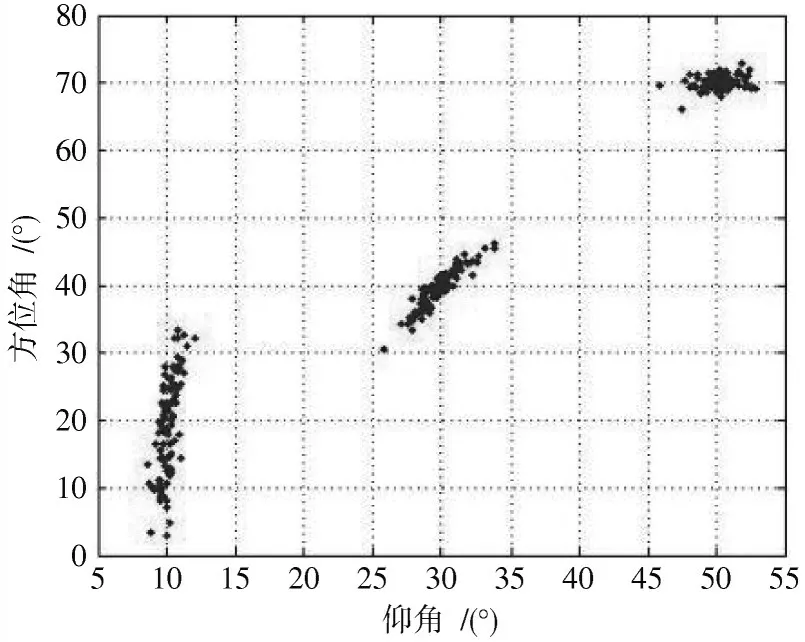
图4 求根MUSIC 算法100 次蒙特卡洛仿真

从图3、图4 可以看出，MUSIC 算法尖峰还是很明显，求根MUSIC 在低仰角时方位角误差很大，甚至大于10°。在快拍数为200，不同信噪比下，各算法均方根误差对比如表1 所示。

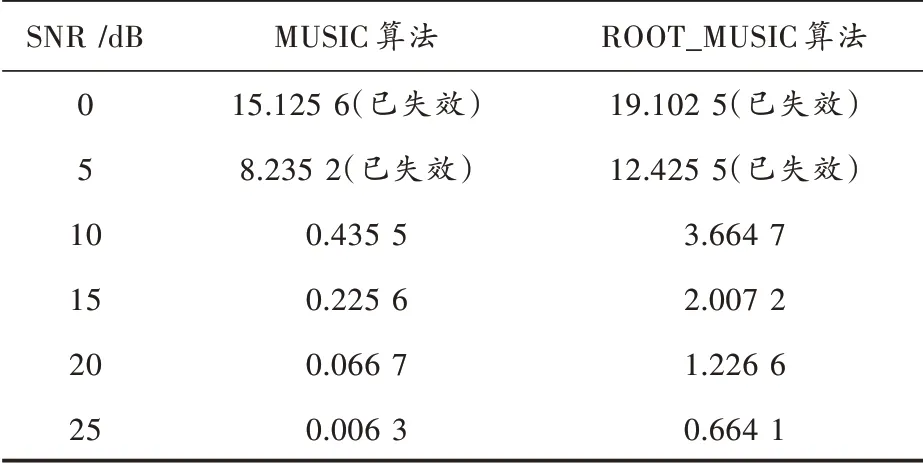
表1 不同信噪比下MUSIC 和ROOT_MUSIC 算法比较

MUSIC 算法平均运算时间为1.181 1 s，求根MUSIC算法平均运算时间为0.093 7 s。由表1 可以分析出求根MUSIC 算法由于不需要全空间搜索，所以计算时间短许多，但由于轴上阵元数限制，均方根误差偏大。MUSIC 算法运算时间过长，不适合实时运算，但精度高，适合事后回放。两种算法均只能在信噪比大于10 dB下才能发挥作用。

3.2 双L 阵型-MUSIC 算法

双L 阵型呈U 型，轴上有6 个阵元，轴上有2 组，每组4 个阵元，公用参考点阵元，假设3 个信号互不相干，角度分别为（10°，20°），（30°，40°），（50°，70°），信噪比选用0 dB，5 dB，10 dB，15 dB，20 dB 和25 dB。MUSIC 算法取1°作为搜索步长，蒙特卡洛次数为100。

在快拍数为200，不同信噪比下，MUSIC 算法均方根误差对比如表2 所示。

表2 不同信噪比双L 阵型MUSIC 算法性能

MUSIC 算法平均用时2.743 9 s。原先考虑使用求根MUSIC 算法作为比较，但仿真后发现轴上4 个阵元大大限制了该算法，使得求根MUSIC 算法经常得出错误的结果，因此不将求根MUSIC算法作为L阵型的比较。

3.3 均匀面阵型-MUSIC、降维MUSIC 和ESPRIT 算法

由于测量通道有限，不能利用全部阵元，所以选取3×4 均匀面阵型作为比较对象，由于求根MUSIC 算法对轴和轴上阵元数量敏感，所以此次面阵算法采用MUSIC、降维MUSIC 和Unitary_ESPRIT 算法作为比较。降维算法优点有：可以实现配对的二维角度估计；只需一次一维局部搜索；运算量大大降低；完全利用信号子空间和噪声子空间；角度估计性能非常接近2D-MUSIC算法。Unitary_ESPRIT 算法通过矩阵，将方向矩阵转变为只有实部，从而降低运算复杂度。角度估计可以根据实部和虚部信息配对好，无需另行计算配对。

仿真条件：均匀面阵型，轴上有4 个阵元，轴上有3 个阵元，呈4×3 排布，假设3 个信号互不相干，角度分别为（10°，20°），（30°，40°），（50°，70°），信噪比选用0 dB，5 dB，10 dB，15 dB，20 dB 和25 dB。使用MUSIC、降维MUSIC 和ESPRIT 算法，MUSIC 算法取1°作为搜索步长，降维MUSIC 选取0.001 精度作为搜索步长。蒙特卡洛次数为100。图5～图7 分别为MUSIC、Unitary_ESPRIT 和降维MUSIC 算法估计性能图，信噪比均为10 dB，快拍数为200。

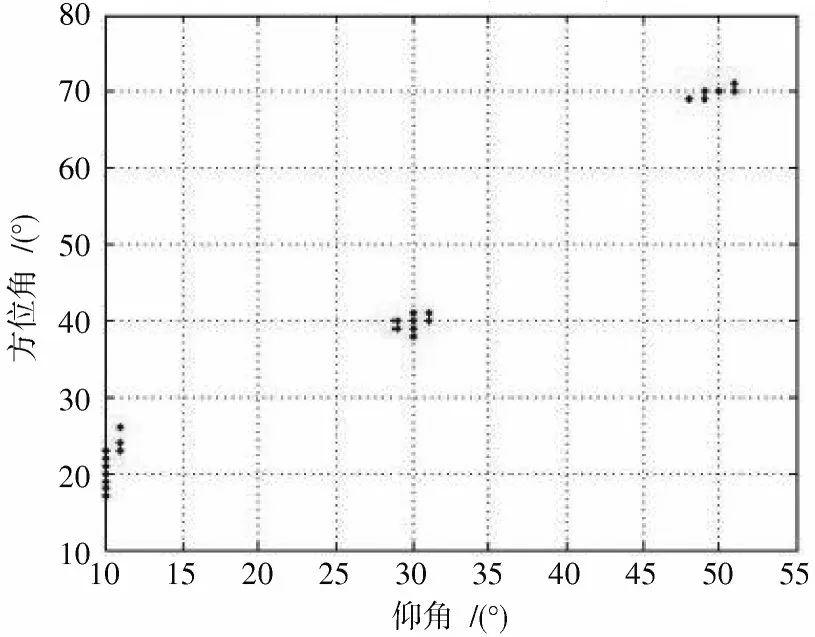
图5 MUSIC 算法估计性能

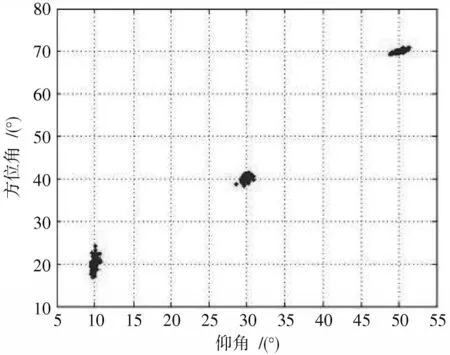
图7 降维MUSIC 算法估计性能

快拍数为200，不同信噪比下各算法均方根误差比较如表3 所示。

表3 不同信噪比均匀面阵型各算法估计性能

图6 Unitary_ESPRIT 算法估计性能

MUSIC 算法平均运算时间为 3.442 1 s，Unitary_ESPRIT 算法平均运算时间为0.001 4 s，降维MUSIC 算法平均运算时间为0.196 0 s。由表3 可以分析出，MUSIC 算法精度高，但由于需要进行二维角度搜索，运算量很大，运算时间过长，不适合作为实时定位算法，而Unitary_ESPRIT 通过矩阵，将方向矩阵转变为只有实部，从而降低运算复杂度，并且根据实部虚部信息获得配对好的角度估计。降维MUSIC 算法计算精度和搜索步长有关，类似于MUSIC算法，但只有一维搜索，所以计算总量相较MUSIC减少很多，高于Unitary_ESPRIT算法。

3.4 “口”字阵型-MUSIC 算法

“口”字阵型每边为4 个阵元，呈正方形排布，假设3 个信号互不相干，角度分别为（10°，20°），（30°，40°），（50°，70°），信噪比选用0 dB、5 dB、10 dB、15 dB、20 dB和25 dB。MUSIC 算法取1°作为搜索步长。蒙特卡洛次数为100，快拍数为200，不同信噪比下MUSIC 算法均方根误差比较如表4 所示。

表4 不同信噪比下“口”字阵型MUSIC 算法性能估计

MUSIC 算法平均运算时间为2.945 5 s。这种非常规阵型适配算法只能使用MUSIC 算法。

3.5 二维面阵阵型适应算法比较

以上分小节介绍了各阵型组成及各阵型下不同算法性能，在快拍数为200，不同信噪比下综合各阵型各算法均方根误差结果如图8 所示，各阵型算法用时如图9 所示。

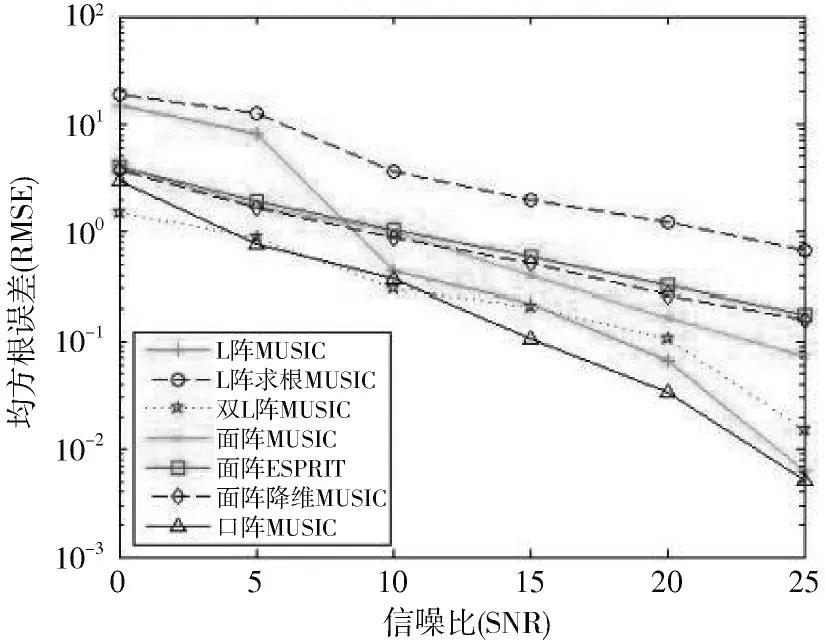
图8 不同信噪比各阵型下算法RMSE 比较

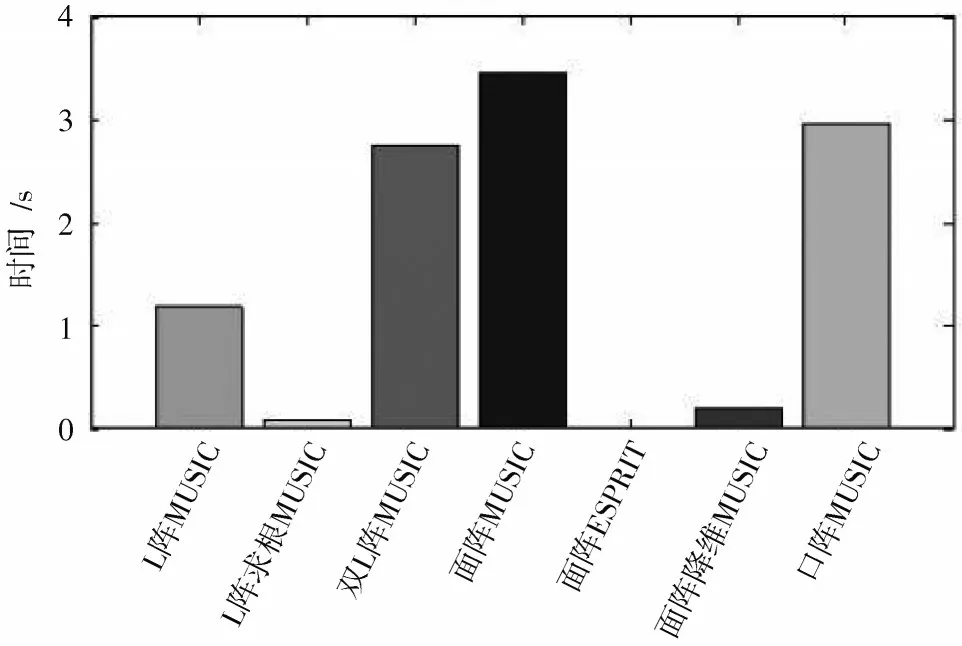
图9 各阵型算法用时比较

从图8 可以得出以下结论：

1）“口”字阵型MUSIC 算法和双L 阵MUSIC 算法在所比较的各阵型算法中均方根误差最优，这与该两种阵型所围成的面积最大有关；

2）均匀面阵型三种算法没有表现很大的差距；

3）求根MUSIC 在各阵型中表现不佳，甚至在其他阵型下无法计算出正确的结果，这与轴最多只有4 个阵元有很大的关系。

由图9 可以看出，面阵MUSIC 算法用时最长，因为每次循环均会计算Kronecker 积，所以较其他阵型MUSIC 用时较长。均匀面阵型ESPRIT 用时最短，可达毫秒级，求根MUSIC 和降维MUSIC 算法用时大幅低于MUSIC 算法。综合各算法均方根误差，MUSIC 算法精度高、用时最长，不适合实时计算，可用于事后数据分析，使用更高性能计算机提高计算速度。L 型阵求根MUSIC 是精度最差的，面阵ESPRIT 和降维MUSIC 计算精度相差不大，所以选取运行时间更短的面阵ESPRIT算法作为系统实时定位算法，相对应的系统阵型为4×3均匀面阵型。

综合以上仿真可得出结论：当信号源深度不定时，可采用均匀面阵型的形式，使用ESPRIT 算法实时解算仰角和方位角。当需要更高精度和不需要实时计算时，可采用“口”字阵型列采集数据，使用更快计算速度的计算机，采用MUSIC 算法进行更高精度解算。