动力蓄电池等效电路模型的仿真研究

彭善涛

动力蓄电池等效电路模型的仿真研究

彭善涛

（苏州建设交通高等职业技术学校，江苏 苏州 215104）

文章通过对动力蓄电池等效电路模型仿真研究中的辨识算法和仿真激励进行研究，确定采用什么算法，以及如何实现该算法，如何设计出持续激励，保证辨识的无偏估计，选取的仿真研究对象是什么类型，从而实现对动力蓄电池等效电路模型参数估计算法。

蓄电池等效电路；辨识；仿真

前言

国内研究蓄电池建模时所用的激励，都是采用HPPC试验或是其它根据经验所得的激励，一定程度上缺乏相对的理论基础[1]。本文通过对蓄电池等效电路模型仿真研究中的辨识算法[2]和仿真激励进行研究，提出一种新的持续、更全面并具有良好自相关性的辨识激励——M序列，为蓄电池等效电路模型参数辨识提供理论基础，目的是满足蓄电池等效电路模型参数估计算法的实现，从而更好的让人们了解、掌握动力蓄电池的具体状况。

1 伪随机信号产生

1.1 M序列的基本特点

在系统模型无误的情况下，输入信号的好坏可以直接影响电路模型的辨识精度。根据特性，我们可以把线性移位寄存器序列（M序列）近似看成是和白噪声一样的简单随机过程，但M序列可以很好模拟工业设备动态运行中的辨识输入信号[3]。

下面讨论线性移位寄存器序列的定义，假设有一无限长二元序列{1,2,···,x,x+1, ···}，这里x= 0或1，其元素x满足下述linear recurrence关系式：

x=a·x⊕a·x⊕···a·x-p（1）

其中a=0或1，⊕表示“模2”相加（即二进制加法），其运算规则如表1所示。=+1，+2，···，1，2，···，x称为该序列的初值。式（1）可用图1所示的移位寄存器电路实现。途中下方的两条线，一条用来传输移位脉冲，另一条用来置初态。

一个p级（即有p个移位寄存器）移位寄存器电路共有2p个状态，只有0和1两种状态。如果所有寄存器的状态都为“0”，则这种状态将保持不变。于是输出总是“0”。只有当初值不全为“0”时，输出信号才不总是“0”。一个p级移位寄存器电路总共有2p−1个非“0”状态。然而一个任意联结的p级移位寄存器并不一定能取遍所有2p−1个非“0”状态。于是，对于一给定的p，x将以某一周期循环，循环周期≤2p−1，当系统的联结使得p级移位寄存器能取遍所有2p−1个非“0”状态时，x的循环周期达到其上界2p−1。这种以（2p-1）字节的最长周期循环的序列叫做M序列。

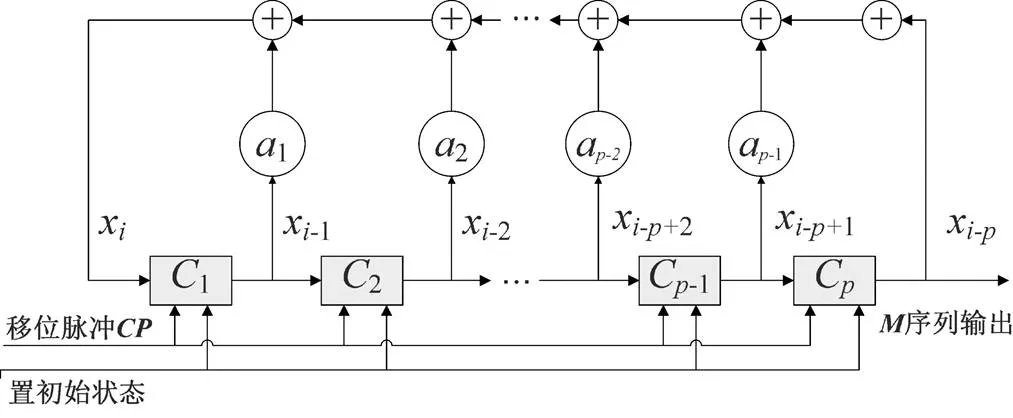
图1 生产M序列的一般结构

为了方便理解，现以四级移位寄存器为例产生线性移位寄存器序列（M序列），如图2所示。

图2 四级移位寄存器产生M序列的结构图

图中⊕表示“模2”和运算，C1，C2，C3 和C4表示四个移位寄存器，1，2，3和4分别表示各移位寄存器的输出，4的输出为产生的线性移位寄存器序列（M序列）。四级移位寄存器的连接方式可用式（2）表示。

表1 四级移位寄存器产生M序列的工作状态

可见，1第（+1）时刻的状态由3和4第时刻状态的异或运算结果决定；2第（+1）时刻的状态由1第时刻状态决定；3第（+1）时刻的状态由2第时刻状态决定；4第（+1）时刻的状态由3第时刻状态决定。设置初始状态为1010，在移位脉冲作用下，寄存器各级状态的变化如表1所示。

1.2 M序列的性质

1.2.1 名词定义

（1）循环长度N=2−1，其中为寄存器的个数。

（2）游程：状态连续出现的段称为游程。

（3）本原多项式：M序列的产生可用移位寄存器序列发生器的本原多项式来确定，一个本原多项式对应一个最大长度的序列，即对应一个M序列。在给定了移位寄存器的级数时，可利用在Matlab编程环境中求出该级移位寄存器可以产生的M序列所有电路结构，也就是求出所有的本原多项式，以4级移位寄存器为例，所有的本原多项式如下：

1++4（3）

1+3+4（4）

1.2.2 M序列性质

性质1：在级M序列的一个循环周期p=2-1bit内，逻辑“0”出现的次数为（-1）/2，逻辑“1”出现的次数为（+1）/2。（注意：这里所谓“次数”的意思是指该值所占的拍数，如连续拍均为“1”，记“1”出现次）。即对于任何阶数的移位寄存器，一个周期内逻辑1出现的次数比逻辑0多一次。

性质2：一个级线性移位寄存器序列（M序列）的游程总数等于2-1，其中“0”游程与“1”游程各占一半。长度为1bit的游程占游程总数1/2；2bit的游程占游程总数1/4；长度为bit的游程占游程总数1/2；但长度为（-1）bit的游程只有一个，为“0”游程；长度为bit的游程只有一个，为“1”游程。以四级移位寄存器为例，每一个周期有15个bit，该15个bit分为8段，其中“0”游程和“1”游程各有4个（无论是几阶寄存器，两者游程数都是相等的）。其中长度为1个bit的有4个，占总段数的1/2；长度为2个bit的有2个，占总段数的1/4；长度为3个bit的有1个（逻辑0），占总段数的1/8；长度为4个bit的有1个（逻辑1），占总段数的1/8。

性质3：改变M序列的初态只不过对该序列进行延迟。这是因为一旦系统的联结确定好了，其2-1个非“0”状态出现的顺序也就确定了。像这一类彼此间只是移位关系的序列称为等价的。同样，改变系统的联结，则可改变这2-1个非“0”状态出现的顺序，从而得到非等价的M序列。

1.3 M序列仿真实现

在Matlab环境中，生成一种M序列可以通过编写M文件实现或者是通过在Matlab/Simulink环境中建立仿真模型实现。下面主要讨论一下如何在Matlab/Simulink环境中建立仿真模型生成所需要的M序列。

以4级移位寄存器为例，4级移位寄存器在Matlab/ Simulink中的仿真模型如图3所示。建立一个M序列的仿真模型步骤如下：

第一步，确定4级移位寄存器的本源多项式，如式（3）和（4）。任意选择其中一个本源多项式（4）如下：

1+3+4

选取每一项的系数（抽头系数）为10011，其中“1”代表移位寄存器处于联结状态，“0”代表移位寄存器断开状态。置初始状态为0001。

第二步，选5个移位寄存器（延迟模块），按序排好，其第二个初始条件（initial conditions）设为0，其他默认为1。

第三步，先把这5个移位寄存器链接起来，第一个输出连第二个输入，以此类推到第5个接out模块，其后面接一个scope模块以便观察信号波形。

第四步，选一个logical operator模块，并从设置中调成XOR，4输入端。

第五步，继续连线，XOR的输出端接第一个移位寄存器的输入端；然后把XOR输入端引到第二个移位寄存器和第三个移位寄存器的连线上，此时XOR还有3个输入端，分别像刚刚那样分别引到第三和第四，第四和第五，第五和out的线上。

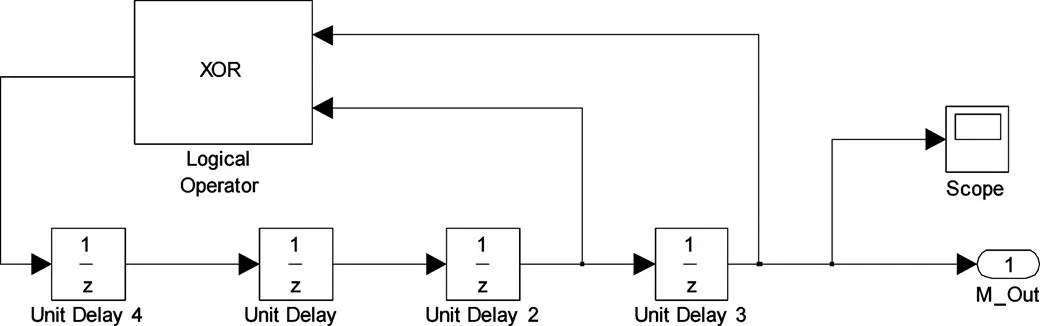
图3 四级移位寄存器模型

图4 生成M序列的取值点

第六步，点击运行仿真模型，运行时间15 s，scope模块中显示的便是M序列的时域波形，图4中用星号表示的点即生成的M序列取值。

从图4中，我们可以获得M序列一个循环周期的取值情况为100010011010111，由此验证了此种生成M序列的方法的正确性和可靠性。

1.4 M序列自相关函数和谱密度函数

上面我们讨论了M序列的生成与性质，接下来我们讨论一下M序列的自相关函数和谱密度函数。

在实际应用中，总把取值为0或1的M序列通过下式：

（）=（1-2x） （5）

变换成取值为或−的M序列。式中x是取0或1的M序列元素，（）是取或−的M序列。

1.4.1 自相关函数

根据自相关函数的定义，M序列的自相关函数可以表示为：

式中Δ是位移脉冲周期（时钟周期），将上式离散化后得到：

显然：

当= 0时，R（）=2（8）

当=Δ时，（1 ≤≤N−1）为整数，

R（）=−2/N（9）

当−Δ≤≤ Δ时，展开式（7）有：

通过前面讨论可知，一个周期内逻辑为“1”的次数为2-1次，故在时间内逻辑为“1”的次数为（2-1）/ Δ。代入式（10）中可以得到：

综合式（8）、（9）和（11）就得到了周期为N△t的M序列自相关函数如下：

同样以四级移位寄存器电路为例，在Matlab环境中实现M序列的自相关函数直观化，探讨M序列的自相关性，如图5所示。

可见，线性移位寄存器序列的自相关函数（当N趋于无穷时）近似于函数，所以线性移位寄存器序列（M序列）是一种较理想的辨识输入信号。

1.4.2 谱密度函数

根据谱密度函数定义，我们可以得到M序列谱密度函数表达式如下：

由于式中自相关函数R（）为偶函数，并且是以周期=N△t重复的，因此式（13）可以表示为：

式（14）经过欧拉变换后得：

将自相关函数式（12）代入式（15）中有：

整理后得到：

将式（18）代入式（17），整理后可得到M序列的谱密度函数为：

分析式（18）可以得知M序列谱密度函数具有如下的一些特点：

（2）M序列的直流成分与N2成反比，增加N可以减小M序列的直流成分。

（3）谱线密度与周期N∆成正比，增加周期，谱线将会加密。

1.5 M序列参数的选取准则

根据先验知识选取M序列作为理想的辨识输入信号，辨识对象的适当选择M序列的循环周期N∆、移位脉冲周期∆和M序列的幅度，才能获得比较理想的辨识结果。这章节主要谈试验之前如何根据一定准则选择M序列的参数N和∆。

果在某一频率范围内谱密度S（）仅下降3 dB，这时就可为谱密度基本是平坦的，可把M序列当做较理想的白噪声处理。频率范围可按上述条件确定，即当S（）下降3 dB时。根据式（18），相当于：

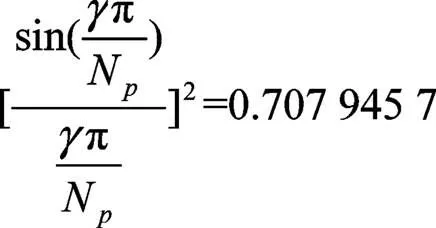
开方后得到：

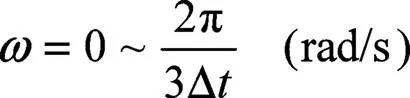
即PRBS有效频带最大值为：

根据式（22）可知，要覆盖被测系统的工作频带，必须满足：

式中max为被测系统的最大工作频率。

按照算法要求，系统的脉冲响应（）应在M序列的一个周期=N∆内衰减到零，因此：

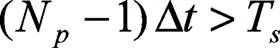
式（24）中，T为系统的过渡过程时间。

综合式（23）、（24）就可以得出确定M序列参数的理论依据：

2 动力蓄电池等效电路模型参数估计算法仿真研究[4]

2.1 动力蓄电池仿真模型的选取

本文中用于替代真实动力蓄电池进行仿真研究的动力蓄电池仿真模型是基于文中提出的改进模型，如图6所示。选取该模型作为替代真实动力蓄电池进行研究，是由于该论文中详细的给定了充电状态中各个SOC下模型中的各个参数取值，如表2所示。同时给定该动力蓄电池模型的单体标称电压为4.2 V，额定安时量为15 Ah。

图6 动力蓄电池仿真模型

表2 充电过程中各个SOC下参数表

SOC(%)RESR(mohm)Rpar(mohm)C(F)Vt(V) 01.345 584.959 294 027.892.908 87 101.300 824.942 294 040.883.155 84 201.261 504.889 494 064.163.374 42 301.145 594.665 664 120.883.564 18 401.106 684.370 214 310.563.730 07 501.110 464.492 624 194.023.858 74 601.174 814.628 824 095.483.949 92 701.200 814.692 584 108.974.025 17 801.250 874.800 124 165.764.080 41 901.259 194.805 634 053.144.137 71 1001.321 875.134 313 992.584.168 82

2.2 确定辨识激励

以SOC=0.5为例来研究动力蓄电池仿真模型的频域特性，将表2中数据代入式（8）中，SOC=0.5下，系统各参数值为：ESR（mohm）= 1.110 46；par（mohm）= 4.492 62；（F）= 4 194.02；t（V）= 3.858 74。得到SOC=0.5下系统的传递函数为：

如图9所示绘制传递函数的BODE图。分析BODE图可观察到在图示点处系统的相位延迟角达到一个峰值，根据已有研究数据可认为此时对应的频率可作为最适合系统的最大工作频率，即fmax= 0.117 7 Hz，其它SOC下，此工作频率也都不超过0.2 Hz，为了确保所选频率能覆盖被测系统的工作频带，在辨识激励参数中，选取fmax= 0.2Hz研究。

根据式（25），要确定M序列参数还必须计算出系统的过渡过程时间T。对于动力蓄电池来说，系统的过渡过程时间等价于系统的极化时间，因此根据公式：

计算出T= 3.733 7 s

根据式（25）来确定M序列的参数如下：

取∆= 1 s。

根据式（25）中：

求得N>4.666 7，取N= 15，即=4四级移位寄存器。

四级移位寄存器模型如图3所示，根据给定蓄电池的额定容量为C=15 Ah，因此选择C/3 =5 A作为输入电流幅值，循环4次，激励电流如图8所示。在M序列取逻辑状态“1”时，赋值电流5 A，作为充电电流；在M序列取逻辑状态“0”时，赋值电流0，即使蓄电池处于静置状态。

图8 M序列激励电流信号图

2.3 等效电路模型参数辨识及其结果分析[5]

SOC=0.5下蓄电池仿真模型如图9所示。运行1 min，4个M序列循环，采样步长为1 s。整个过程中，蓄电池增加量仅为0.045 7 Ah，可近似的认为在整个过程中蓄电池的SOC没变化，相应蓄电池开路电压也没变化。

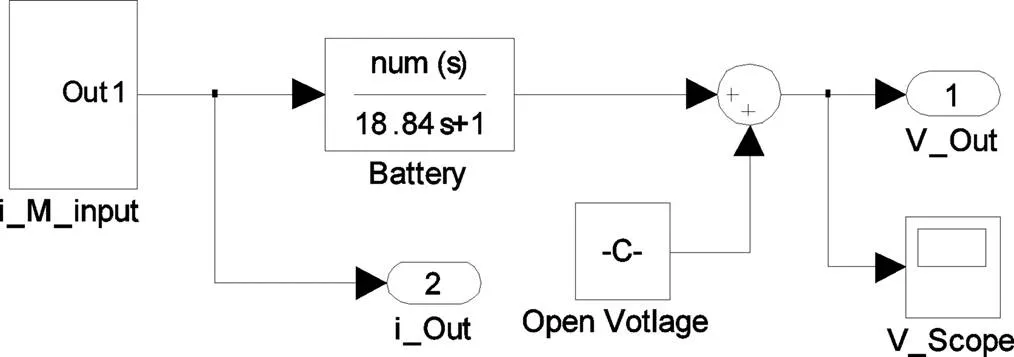
图9 蓄电池仿真模型

运行结果如图10所示。

采集输入i和输出v数据，使用最小二乘法完成算法对模型式（13）进行参数辨识，根据式（11）—（14）求出各个模型参数值，表3所示为误差对比。

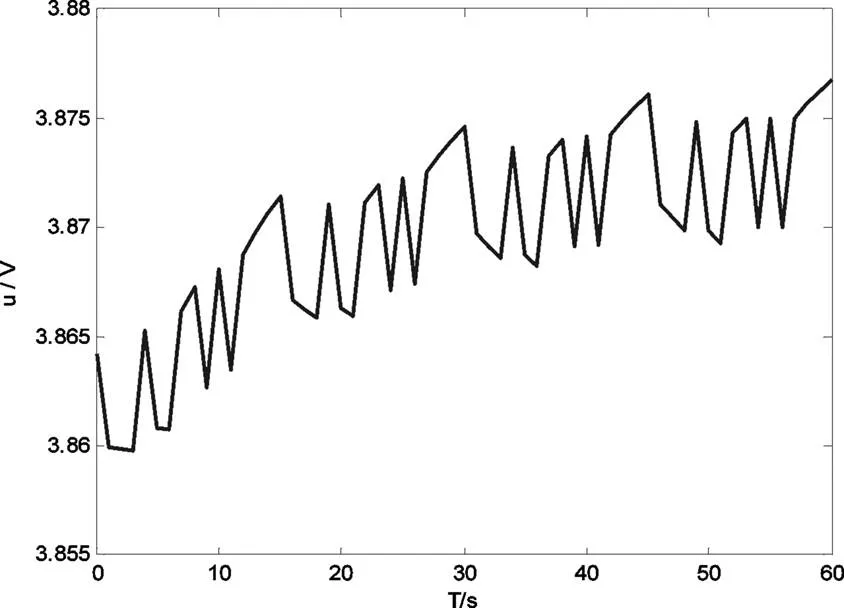
图10 仿真输出电压图

表3 参数真实值和辨识值的误差对比

RESR(mohm)Rpar(mohm)C(F)Vt(V) 参数真实值1.110 464.492 624 194.023.858 74 参数辨识值1.110 464.492 624 194.023.858 74 辨识误差0000

其余各个SOC下辨识结果和SOC=0.5的一样，限于篇幅的限制，就不一一列举。

3 总结

本文通过仿真试验，针对动力蓄电池仿真模型的选取以及辨识的理论依据推导，辨识激励的确定以及辨识结果的分析，进行动力蓄电池等效电路模型参数的估计。结合生成M序列的相关参数特性，最后得出采取新的M序列辨识激励对动力蓄电池系统进行等效电路模型参数辨识的研究是可靠有效的结论，为下一步进行试验研究提供了理论基础和依据。

[1] 符晓玲,商云龙,崔纳新. 电动汽车电池管理系统研究现状及发展趋势[J].电力电子技术,2011,45(12):27-30+89.

[2] 司伟,冯长江,黄天辰.储能蓄电池参数辨识研究进展[J].飞航导弹, 2018(07):71-75.

[3] 周全.一种纯电动汽车蓄电池SOC估算的实现方案[J].淮海工学院学报(自然科学版),2014,23(01):30-33.

[4] 周亚运.锂离子动力电池模型及SOC估算研究[D].柳州:广西科技大学,2018.

[5] 彭善涛.电动汽车动力蓄电池等效电路模型参数估计研究[D].苏州:苏州大学,2017.

Simulation Research on Equivalent Circuit Model of Traction Battery

PENG Shantao

( Suzhou Institute of Construction and Communications, Jiangsu Suzhou 215104 )

In this paper, the identification algorithm in the simulation study of the equivalent circuit model of power battery is studied and the simulation excitation is studied,determine what algorithm to use and how to implement it.Research how to design the continuous excitation to ensure the unbiased estimation of identification,what type of simulation research object is selected,so as to realize the parameter estimation algorithm for the equivalent circuit model of power battery.

Battery equivalent circuit;Identify;Emulation

U463.63+3

A

1671-7988(2021)20-09-06

U463.63+3

A

1671-7988(2021)20-09-06

10.16638/j.cnki.1671-7988.2021.020.003

彭善涛，就职于苏州建设交通高等职业技术学校。